No CrossRef data available.
Article contents
Analysis of semilocal convergence for ameliorated super-Halley methods with less computation for inversion
Published online by Cambridge University Press: 01 October 2016
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, the semilocal convergence for ameliorated super-Halley methods in Banach spaces is considered. Different from the results in [J. M. Gutiérrez and M. A. Hernández, Comput. Math. Appl. 36 (1998) 1–8], these ameliorated methods do not need to compute a second derivative, the computation for inversion is reduced and the 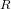 $R$ -order is also heightened. Under a weaker condition, an existence–uniqueness theorem for the solution is proved.
$R$ -order is also heightened. Under a weaker condition, an existence–uniqueness theorem for the solution is proved.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2016
References
Argyros, I. K. and Chen, D., ‘Results on the Chebyshev method in Banach spaces’, Proyecciones
12 (1993) no. 2, 119–128.Google Scholar
Argyros, I. K., George, S. and Magreñán, Á. A., ‘Local convergence for multi-point-parametric Chebyshev–Halley-type methods of high convergence order’, J. Comput. Appl. Math.
282 (2015) 215–224.Google Scholar
Argyros, I. K. and Magreñán, Á. A., ‘A study on the local convergence and the dynamics of Chebyshev–Halley-type methods free from second derivative’, Numer. Algor.
71 (2016) 1–23.Google Scholar
Candela, V. and Marquina, A., ‘Recurrence relations for rational cubic methods I: the Halley method’, Computing
44 (1990) 169–184.Google Scholar
Candela, V. and Marquina, A., ‘Recurrence relations for rational cubic methods II: the Chebyshev method’, Computing
45 (1990) 355–367.Google Scholar
Ezquerro, J. A. and Hernández, M. A., ‘On the R-order of the Halley method’, J. Math. Anal. Appl.
303 (2005) 591–601.Google Scholar
Gutiérrez, J. M. and Hernández, M. A., ‘A family of Chebyshev–Halley type methods in Banach spaces’, Bull. Aust. Math. Soc.
55 (1997) 113–130.Google Scholar
Gutiérrez, J. M. and Hernández, M. A., ‘Recurrence relations for the super-Halley method’, Comput. Math. Appl.
36 (1998) 1–8.CrossRefGoogle Scholar
Hernández, M. A., ‘Second-derivative-free variant of the Chebyshev method for nonlinear equations’, J. Optim. Theory Appl.
104 (2000) no. 3, 501–515.Google Scholar
Ostrowski, A. M.,
Solution of equations in Euclidean and Banach spaces
, 3rd edn (Academic Press, New York, 1973).Google Scholar
Powell, M. J. D., ‘On the convergence of trust region algorithms for unconstrained minimization without derivatives’, Comput. Optim. Appl.
53 (2012) 527–555.Google Scholar


