Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dragila, R.
Maddever, R. A. M.
and
Luther-Davies, B.
1987.
Frequency modulation of laser radiation reflected from an expanding laser-produced plasma.
Physical Review A,
Vol. 36,
Issue. 11,
p.
5292.
Amiranoff, F.
Briand, F.
and
Labaune, C.
1987.
Three-halves harmonic measurements on 0.53 μm laser produced plasmas.
The Physics of Fluids,
Vol. 30,
Issue. 7,
p.
2221.
Gu, Min
Tan, Weihan
Lin, Zungi
Chen, Wenhua
Zheng, Yuxia
Yu, Wenyan
and
Deng, Ximing
1988.
Evidence, from space resolved spectra, of 2ω0 harmonic generation in laser irradiated plasma filaments.
Optics Communications,
Vol. 66,
Issue. 1,
p.
35.
Nicolás, J. A.
Sanz, J.
Sanmartín, J. R.
and
Hilario, J.
1989.
Non-uniform target illumination in deflagration regime. Refractive smoothing.
Laser and Particle Beams,
Vol. 7,
Issue. 3,
p.
627.
Kasotakis, G.
Cicchitelli, L.
Hora, H.
and
Stening, R. J.
1989.
Volume compression and volume ignition of laser driven fusion pellets.
Laser and Particle Beams,
Vol. 7,
Issue. 3,
p.
511.
Maddever, R. A. M.
Luther-Davies, B.
and
Dragila, R.
1990.
Pulsation of 1ω0and 2ω0emission for laser-produced plasmas. II. Theory.
Physical Review A,
Vol. 41,
Issue. 4,
p.
2165.
Goldsworthy, M. P.
Hora, H.
and
Stening, R. J.
1990.
Double layer effects causing nearly uniform striated second harmonic emission from a laser irradiated plasma corona.
Laser and Particle Beams,
Vol. 8,
Issue. 1-2,
p.
33.
Miley, George H.
Hora, Heinrich
Cicchitelli, Lorenzo
Kasotakis, Gregorios V.
and
Stening, Robert J.
1991.
An Advanced Fuel Laser Fusion and Volume Compression ofp-11B Laser-Driven Targets.
Fusion Technology,
Vol. 19,
Issue. 1,
p.
43.
Min, Gu
and
Hora, H.
1991.
Pulsation of laser–plasma interaction explained by density ripple buildup and relaxation for understanding smoothing by random-phase plate, ISI, and broadband.
Laser and Particle Beams,
Vol. 9,
Issue. 2,
p.
381.
Giulietti, D.
Biancalana, V.
Batani, D.
Giulietti, A.
Gizzi, L.
Nocera, L.
and
Schifano, E.
1991.
Three-half harmonic generation in laser-plasma interaction: Evidence for plasmon propagation.
Il Nuovo Cimento D,
Vol. 13,
Issue. 7,
p.
845.
Peyser, T. A.
Manka, C. K.
Obenschain, S. P.
and
Kearney, K. J.
1991.
Reduction of 3ω/2 emission from laser-produced plasmas with broad bandwidth, induced spatial incoherence at 0.53 μm.
Physics of Fluids B: Plasma Physics,
Vol. 3,
Issue. 6,
p.
1479.
Aydin, M.
Min, Gu
and
Hora, H.
1992.
10-ps pulsation of laser plasma explained hydrodynamically by self-generated Bragg ripples and their decay and avoidance by smoothing.
Laser and Particle Beams,
Vol. 10,
Issue. 1,
p.
155.
Boreham, B.W.
Hora, H.
Aydin, M.
Eliezer, S.
Goldsworthy, M.P.
Min, Gu
Gahatak, A.K.
Lalousis, P.
Stening, R.J.
Szichman, H.
Hora, H.
Aydin, M.
Eliezer, S.
Goldsworthy, M.P.
Min, Gu
Gahatak, A.K.
Lalousis, P.
Szichman, H.
Maddever, R.A.M.
Luther-Davies, B.
Baldwin, K.G.H.
Maddever, R.A.M.
and
Rode, A.V.
1997.
Beam smoothing and temporal effects:Optimized preparation of laser beams for direct-drive inertial confinement fusion.
Laser and Particle Beams,
Vol. 15,
Issue. 2,
p.
277.
Lin, Zunqi
Lei, Anle
Fan, Wei
Zhou, Shenlei
and
Wang, Li
2013.
An important effect of filamentation instability on laser fusion physical processes.
High Power Laser Science and Engineering,
Vol. 1,
Issue. 3-4,
p.
110.
Kang, N.
Lin, Z.
Shen, B.
Liu, H.
Lei, A.
Fan, W.
Zhou, S.
and
Wang, L.
2016.
Two-dimensional particle-in-cell simulation of small-scale laser–plasma interactions with laser-produced plasma jets.
Journal of the Optical Society of America B,
Vol. 33,
Issue. 5,
p.
932.
Kang, N
Liu, H
Lin, Z
Lei, A
Zhou, S
Fang, Z
An, H
Li, K
and
Fan, W
2017.
Spectrally and angularly resolved measurements of three-halves harmonic emission from laser-produced plasmas.
Plasma Physics and Controlled Fusion,
Vol. 59,
Issue. 10,
p.
105011.
Kang, Ning
Liu, Huiya
Lei, Anle
Ji, Shengzhe
and
Zhou, Shenlei
2020.
Spatially and temporally discontinuous two-plasmon decay with relatively low laser irradiance.
Plasma Physics and Controlled Fusion,
Vol. 62,
Issue. 12,
p.
125001.
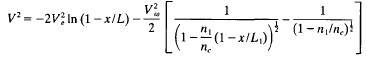 when
when 

