Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Armbrüster, G.
Majer, B.
Reimann, U.
and
Toepffer, C.
1992.
Transient effects in strongly correlated nonequilibrium plasmas.
Laser and Particle Beams,
Vol. 10,
Issue. 2,
p.
365.
Dufty, James W.
1993.
Model for Ion Collision Rate and Kinetic Equation.
Contributions to Plasma Physics,
Vol. 33,
Issue. 5-6,
p.
513.
Armbrüster, G.
and
Toepffer, C.
1993.
Temperature relaxation of plasmas in a magnetic field.
Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment,
Vol. 333,
Issue. 2-3,
p.
282.
Chiu, G.
Ng, A.
and
Forsman, A.
1997.
Effect of electron-ion equilibration on optical emission from a shock wave.
Physical Review E,
Vol. 56,
Issue. 5,
p.
R4947.
Gericke, D. O.
Murillo, M. S.
and
Schlanges, M.
2002.
Dense plasma temperature equilibration in the binary collision approximation.
Physical Review E,
Vol. 65,
Issue. 3,
David, N.
and
Hooker, S. M.
2003.
Molecular-dynamic calculation of the relaxation of the electron energy distribution function in a plasma.
Physical Review E,
Vol. 68,
Issue. 5,
Gericke, D O
2005.
Kinetic approach to temperature relaxation in dense plasmas.
Journal of Physics: Conference Series,
Vol. 11,
Issue. ,
p.
111.
Gericke, D O
Bornath, Th
and
Schlanges, M
2006.
Energy transfer and potential energy contributions in dense two-temperature plasmas.
Journal of Physics A: Mathematical and General,
Vol. 39,
Issue. 17,
p.
4739.
Jeon, B.
Foster, M.
Colgan, J.
Csanak, G.
Kress, J. D.
Collins, L. A.
and
Grønbech-Jensen, N.
2008.
Energy relaxation rates in dense hydrogen plasmas.
Physical Review E,
Vol. 78,
Issue. 3,
Murillo, Michael S.
and
Dharma-wardana, M. W. C.
2008.
Temperature Relaxation in Hot Dense Hydrogen.
Physical Review Letters,
Vol. 100,
Issue. 20,
Rose, D. V.
Genoni, T. C.
Welch, D. R.
Clark, R. E.
Campbell, R. B.
Mehlhorn, T. A.
and
Flicker, D. G.
2009.
Particle-in-cell and hypernetted chain models of two-component, two-temperature coupled classical plasmas.
Physics of Plasmas,
Vol. 16,
Issue. 10,
Vorberger, J.
Gericke, D. O.
Bornath, Th.
and
Schlanges, M.
2010.
Energy relaxation in dense, strongly coupled two-temperature plasmas.
Physical Review E,
Vol. 81,
Issue. 4,
Cho, B. I.
Ogitsu, T.
Engelhorn, K.
Correa, A. A.
Ping, Y.
Lee, J. W.
Bae, L. J.
Prendergast, D.
Falcone, R. W.
and
Heimann, P. A.
2016.
Measurement of Electron-Ion Relaxation in Warm Dense Copper.
Scientific Reports,
Vol. 6,
Issue. 1,
Fletcher, L. B.
Vorberger, J.
Schumaker, W.
Ruyer, C.
Goede, S.
Galtier, E.
Zastrau, U.
Alves, E. P.
Baalrud, S. D.
Baggott, R. A.
Barbrel, B.
Chen, Z.
Döppner, T.
Gauthier, M.
Granados, E.
Kim, J. B.
Kraus, D.
Lee, H. J.
MacDonald, M. J.
Mishra, R.
Pelka, A.
Ravasio, A.
Roedel, C.
Fry, A. R.
Redmer, R.
Fiuza, F.
Gericke, D. O.
and
Glenzer, S. H.
2022.
Electron-Ion Temperature Relaxation in Warm Dense Hydrogen Observed With Picosecond Resolved X-Ray Scattering.
Frontiers in Physics,
Vol. 10,
Issue. ,
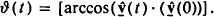 . Extrapolating the short-time behaviour ϑshort(t), one obtains the collision time tc by setting ϑshort(tc) = π/2. We have shown with the help of computer simulations that this procedure is ambiguous, as we can clearly distinguish three regimes for ϑ(t). There is always an initial ballistic regime with ϑ(t) ∝ t with dominant pairwise interactions. This lasts up to times α/υth where α is the mean distance between the particles and υth their mean velocity. This is followed by a diffusive regime with ϑ(t) ∝ t½, which is characterized by many small-angle scattering events. Eventually, this diffusion will lead to a uniform distribution of the directions of the velocity. So ϑ(t) will saturate towards π/2 in a third asymptotic regime. For large plasma parameters Γ ≫ 1, this asymptotic behaviour will be modulated by a damped oscillation of ϑ(t) with the plasma frequency. For such strongly coupled plasmas the diffusive regime is suppressed and one observes a direct transition from the initial ballistic to the asymptotic collective regime characterized by the plasma oscillation. Parameters such as the diffusion constant and the transition times are estimated with the help of analytical models.
. Extrapolating the short-time behaviour ϑshort(t), one obtains the collision time tc by setting ϑshort(tc) = π/2. We have shown with the help of computer simulations that this procedure is ambiguous, as we can clearly distinguish three regimes for ϑ(t). There is always an initial ballistic regime with ϑ(t) ∝ t with dominant pairwise interactions. This lasts up to times α/υth where α is the mean distance between the particles and υth their mean velocity. This is followed by a diffusive regime with ϑ(t) ∝ t½, which is characterized by many small-angle scattering events. Eventually, this diffusion will lead to a uniform distribution of the directions of the velocity. So ϑ(t) will saturate towards π/2 in a third asymptotic regime. For large plasma parameters Γ ≫ 1, this asymptotic behaviour will be modulated by a damped oscillation of ϑ(t) with the plasma frequency. For such strongly coupled plasmas the diffusive regime is suppressed and one observes a direct transition from the initial ballistic to the asymptotic collective regime characterized by the plasma oscillation. Parameters such as the diffusion constant and the transition times are estimated with the help of analytical models.