Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T01:23:21.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Relativistic and ponderomotive self-focusing of a laser pulse in magnetized plasma

Published online by Cambridge University Press:  22 October 2012

Anamika Sharma  and
V.K. Tripathi
Anamika Sharma*
Affiliation:
Department of Physics, Indian Institute of Technology Delhi, New Delhi, India
V.K. Tripathi
Affiliation:
Department of Physics, Indian Institute of Technology Delhi, New Delhi, India
*
Address correspondence and reprint requests to: Anamika Sharma, Department of Physics, Indian Institute of Technology Delhi, New Delhi-110016, India. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The self-focusing of an intense right circularly polarized Gaussian laser pulse in magnetized plasma is studied. The ions are taken to be immobile and relativistic mass effect is incorporated in both the plasma frequency (ωp) and the electron cyclotron frequency (ωc) while determining the ponderomotive force on electrons. The ponderomotive force causes electron expulsion when the effective electron cyclotron frequency is below twice the laser frequency. The nonlinear plasma dielectric function due to ponderomotive and relativistic effects is derived, which is then employed in beam-width parameter equation to study the self-focusing of the laser beam. From this, we estimate the importance of relativistic self-focusing in comparison with ponderomotive self-focusing at moderate laser intensities. The beam width parameter decreases with magnetic field indicating better self-focusing. 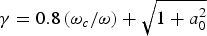When the laser intensity is very high, the relativistic gamma factor can be modeled as ${\rm \gamma} = 0.8\left({{{{\rm \omega} _c } / {\rm \omega} }} \right)+ \sqrt {1 + a_0^2 }$γ=0.8(ωc/ω)+1+a02 where ω and a0 are the laser frequency and the normalized laser field strength, respectively. The cyclotron effects on the self-focusing of laser pulse are reduced at high field strengths.

Keywords

Laser pulseMagnetized plasmaPonderomotive effectsRelativistic effectsSelf-focusing
Type
Research Article
Information
Laser and Particle Beams , Volume 30 , Issue 4 , December 2012 , pp. 659 - 664
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Brandi, H.S., Manus, C., Mainfray, G. & Lehner, T. (1993). Relativistic self-focusing of ultraintense laser pulses in inhomogeneous underdense plasmas. Phys. Rev. E 47, 3780–3783.CrossRefGoogle ScholarPubMed
Chen, X.L. & Sudan, R.N. (1993). Necessary and sufficient conditions for self-focusing of short ultraintense laser pulse in underdense plasma. Phys. Rev. Lett. 70, 2082–2085.CrossRefGoogle ScholarPubMed
Chessa, P., Wispelaere, E. De., Dorchies, F., Malka, V.J., Marques, R., Hamoniaux, G., Mora, P. & Amiranoff, F. (1999). Temporal and angular resolution of the ionization-induced refraction of a short laser pulse in a helium plasma. Phys. Rev. Lett. 82, 552–555.CrossRefGoogle Scholar
Durfee, C.G. & Milchberg, H.M. (1993). Light pipe for high intensity laser pulses. Phys. Rev. Lett. 71, 2409–2412.CrossRefGoogle ScholarPubMed
Esarey, E., Sprangle, P., Krall, J. & Ting, A. (1996). Overview of plasma-based accelerator concept. IEEE Trans. Plasma Sci. PS-24, 252–288.CrossRefGoogle Scholar
Esarey, E., Sprangle, P., Krall, J. & Ting, A. (1997). Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE J. Quan. Electron. 33(11), 1879–1914.CrossRefGoogle Scholar
Feit, M.D., Komashko, A.M., Musher, S.L., Rubenchik, A.M. & Turitsyn, S.K. (1998). Electron cavitation and relativistic self-focusing in underdense plasma. Phys. Rev. E 57, 7122–7125.CrossRefGoogle Scholar
Ghorbanalilu, M. (2010). Focusing of intense laser beam by a thin axially magnetized lens. Phys. Plasmas 17, 023111–023111-5.CrossRefGoogle Scholar
Hafizi, B., Ting, A., Sprangle, P. & Hubbard, R.F. (2000). Relativistic focusing and ponderomotive channeling of intense laser beam. Phys. Rev. E 62, 4120–4125.CrossRefGoogle Scholar
Jha, P., Mishra, R.K., Upadhyaya, A.K. & Raj, G. (2007). Spot-size evolution of laser beam propagating in plasma embedded in axial magnetic field. Phys. Plasmas 14, 114504–114504-3.CrossRefGoogle Scholar
Kaur, S. & Sharma, A.K. (2009). Self-focusing of a laser pulse in plasma with periodic density ripple. Laser Part. Beams 27,193–199.CrossRefGoogle Scholar
Liu, C.S. & Tripathi, V.K. (2000). Laser frequency upshift, self-defocusing and ring formation in tunnel ionizing gases and plasmas. Phys. Plasmas 7, 4360–4363.CrossRefGoogle Scholar
Najmudin, Z., Tatarakis, M., Pukhov, A., Clark, E.L., Clarke, R.J., Dangor, A.E., Faure, J., Malka, V., Neely, D., Santala, M.I.K. & Krushelnick, K. (2001). Phys. Rev. Lett. 87, 215004–215008.CrossRefGoogle Scholar
Osman, F., Castillo, R. & Hora, H. (1999). Relativistic and ponderomotive self-focusing at laser-plasma interaction. J. Plasma Phys. 61, 263–273.CrossRefGoogle Scholar
Pukhov, A. & Myer-Ter-Vehn, J. (1996). Relativistic magnetic self-channeling of light in near-critical plasma: Three-dimensional particle-in cell simulation. Phys. Rev. Lett. 76, 3975–3978.CrossRefGoogle ScholarPubMed
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1976). Progress in Optics; Amsterdam: North Holland, Vol. 13, p. 169.Google Scholar
Sodha, M.S. & Tripathi, V.K. (1977). Steady-state self-focusing and filamentation of whistlers in a plasma. J. Appl. Phys. 45(3), 1078–1084.CrossRefGoogle Scholar
Stenzel, R.L. (1975). Self-ducting of large-amplitude whistler waves. Phys. Rev. Lett. 35, 574–577.CrossRefGoogle Scholar
Sun, G-Z., Ott, E.Y., Lee, C. & Guzdar, P. (1987). Self-focusing of short intense pulses in plasmas. Phys. Fluids 30, 526–532.CrossRefGoogle Scholar
Tripathi, V.K., Taguchi, T. & Liu, C.S. (2005). Plasma channel charging by an intense short pulse laser and ion Coulomb explosion. Phys. Plasmas 12, 043106–043106-7.CrossRefGoogle Scholar