Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T01:19:31.132Z Has data issue: false hasContentIssue false
  • English
  • Français

The Distribution of Quasi-Ranges in Samples from Rectangular and Exponential Distributions

Published online by Cambridge University Press:  11 August 2014

A. Ghosal
Get access

Extract

For the past few years, stimulating research has been carried out on ordered statistics. Linear combinations of the sample ordered values are used to provide estimates of parameters of the population from which the sample is drawn. Such statistics are termed systematic by Mosteller. They are in common use, because they provide simple solutions of parametric problems of statistical estimation. Often they are inefficient, but this drawback is sometimes more than offset by the ease with which the calculations are performed.

Mosteller drew attention to the possible use of the statistics Wr , which he called quasi-range of rth order and defined as

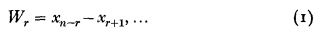
where x 1, x 2,…, x n are ordered observations in a sample of n from a population f(x) (x 1 < x 2 < … < xn ). The distributions of quasiranges in samples drawn from a normal population have been studied by Godwin and Cadwell.

Type
Research Article
Information
Journal of the Staple Inn Actuarial Society , Volume 14 , Issue 1 , January 1956 , pp. 94 - 101
Copyright
Copyright © Institute of Actuaries Students' Society 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cadwell, J. H. (1953). The distribution of quasi-ranges in samples from normal population. Ann. Math. Statist. 24, 603.Google Scholar
Godwin, H. J. (1949). Some low moments of statistics. Ann. Math. Statist. 20, 279.Google Scholar
Godwin, H. J. (1949). On the estimation of dispersion by linear systematic statistics. Biometrika, 36, 92.Google Scholar
Lloyd, E. H. (1952). Least squares estimation of location and scale parameters using order statistics. Biometrika, 39, 88.Google Scholar
Mood, A. M. (1950). Introduction to the Theory of Statistics. New York: McGraw Hill Book Co. Google Scholar
Mosteller, F. (1946). On some useful inefficient statistics. Ann. Math. Statist. 17, 377.Google Scholar
Sarhan, A. E. (1954). Estimation of the mean and standard deviation by order statistics. Ann. Math. Statist. 25, 317.Google Scholar