Claim Frequency analysis in Motor Insurance

Extract

It is a characteristic of motor insurance data that policies can be classified by many different factors, for example age of policyholder, No Claims Discount (N.C.D.), status, amount of voluntary excess and so on. The most ‘complete’ data on the experience of a portfolio would be a classification of each policy by the various rating factors, and by the number of claims which occur on that policy in the period of exposure. It will be shown that provided certain conditions are fulfilled, useful results can be obtained with far less information.

The model selected assumes that the claim frequency of a policy (that is, the average number of claims per year) is of the form

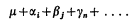
where α, β, γ,.. are rating factors (age of policyholder, N.C.D., status, etc.) and the subscripts range over the different values of the factor (e.g. if N.C.D. has five levels, the subscript of that factor can take five levels). The μ in the formula is a parameter whose use will be explained later.