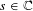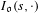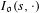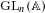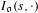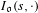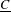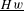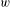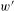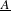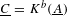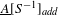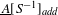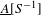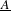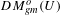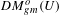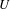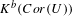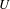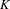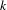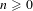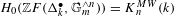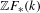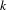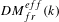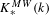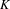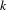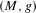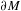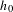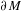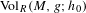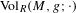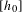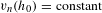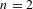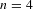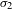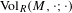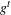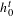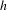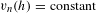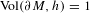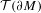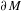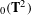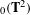We establish an infinitesimal version of the Jacquet-Rallis trace formula for general linear groups. Our formula is obtained by integrating a kernel truncated à la Arthur multiplied by the absolute value of the determinant to the power s\in \mathbb{C}$s\in \mathbb{C}$. It has a geometric side which is a sum of distributions I_{\mathfrak{o}}(s,\cdot )$I_{\mathfrak{o}}(s,\cdot )$ indexed by the invariants of the adjoint action of \text{GL}_{n}(\text{F})$\text{GL}_{n}(\text{F})$ on \mathfrak{gl}_{n+1}(\text{F})$\mathfrak{gl}_{n+1}(\text{F})$ as well as a «spectral side» consisting of the Fourier transforms of the aforementioned distributions. We prove that the distributions I_{\mathfrak{o}}(s,\cdot )$I_{\mathfrak{o}}(s,\cdot )$ are invariant and depend only on the choice of the Haar measure on \text{GL}_{n}(\mathbb{A})$\text{GL}_{n}(\mathbb{A})$. For regular semi-simple classes \mathfrak{o}$\mathfrak{o}$, I_{\mathfrak{o}}(s,\cdot )$I_{\mathfrak{o}}(s,\cdot )$ is a relative orbital integral of Jacquet-Rallis. For classes \mathfrak{o}$\mathfrak{o}$ called relatively regular semi-simple, we express I_{\mathfrak{o}}(s,\cdot )$I_{\mathfrak{o}}(s,\cdot )$ in terms of relative orbital integrals regularised by means of zeta functions.

In this paper we demonstrate that non-commutative localizations of arbitrary additive categories (generalizing those defined by Cohn in the setting of rings) are closely (and naturally) related to weight structures. Localizing an arbitrary triangulated category \text{}\underline{C}$\text{}\underline{C}$ by a set S$S$ of morphisms in the heart \text{}\underline{Hw}$\text{}\underline{Hw}$ of a weight structure w$w$ on it one obtains a triangulated category endowed with a weight structure w^{\prime }$w^{\prime }$. The heart of w^{\prime }$w^{\prime }$ is a certain version of the Karoubi envelope of the non-commutative localization \text{}\underline{Hw}[S^{-1}]_{\mathit{add}}$\text{}\underline{Hw}[S^{-1}]_{\mathit{add}}$ (of \text{}\underline{Hw}$\text{}\underline{Hw}$ by S$S$). The functor \text{}\underline{Hw}\rightarrow \text{}\underline{Hw}[S^{-1}]_{\mathit{add}}$\text{}\underline{Hw}\rightarrow \text{}\underline{Hw}[S^{-1}]_{\mathit{add}}$ is the natural categorical version of Cohn’s localization of a ring, i.e., it is universal among additive functors that make all elements of S$S$ invertible. For any additive category \text{}\underline{A}$\text{}\underline{A}$, taking \text{}\underline{C}=K^{b}(\text{}\underline{A})$\text{}\underline{C}=K^{b}(\text{}\underline{A})$ we obtain a very efficient tool for computing \text{}\underline{A}[S^{-1}]_{\mathit{add}}$\text{}\underline{A}[S^{-1}]_{\mathit{add}}$; using it, we generalize the calculations of Gerasimov and Malcolmson (made for rings only). We also prove that \text{}\underline{A}[S^{-1}]_{\mathit{add}}$\text{}\underline{A}[S^{-1}]_{\mathit{add}}$ coincides with the ‘abstract’ localization \text{}\underline{A}[S^{-1}]$\text{}\underline{A}[S^{-1}]$ (as constructed by Gabriel and Zisman) if S$S$ contains all identity morphisms of \text{}\underline{A}$\text{}\underline{A}$ and is closed with respect to direct sums. We apply our results to certain categories of birational motives DM_{gm}^{o}(U)$DM_{gm}^{o}(U)$ (generalizing those defined by Kahn and Sujatha). We define DM_{gm}^{o}(U)$DM_{gm}^{o}(U)$ for an arbitrary U$U$ as a certain localization of K^{b}(Cor(U))$K^{b}(Cor(U))$ and obtain a weight structure for it. When U$U$ is the spectrum of a perfect field, the weight structure obtained this way is compatible with the corresponding Chow and Gersten weight structures defined by the first author in previous papers. For a general U$U$ the result is completely new. The existence of the corresponding adjacentt$t$-structure is also a new result over a general base scheme; its heart is a certain category of birational sheaves with transfers over U$U$.

Given a field k$k$ of characteristic zero and n\geqslant 0$n\geqslant 0$, we prove that H_{0}(\mathbb{Z}F(\unicode[STIX]{x1D6E5}_{k}^{\bullet },\mathbb{G}_{m}^{\wedge n}))=K_{n}^{MW}(k)$H_{0}(\mathbb{Z}F(\unicode[STIX]{x1D6E5}_{k}^{\bullet },\mathbb{G}_{m}^{\wedge n}))=K_{n}^{MW}(k)$, where \mathbb{Z}F_{\ast }(k)$\mathbb{Z}F_{\ast }(k)$ is the category of linear framed correspondences of algebraic k$k$-varieties, introduced by Garkusha and Panin [The triangulated category of linear framed motives DM_{fr}^{eff}(k)$DM_{fr}^{eff}(k)$, in preparation] (see [Garkusha and Panin, Framed motives of algebraic varieties (after V. Voevodsky), Preprint, 2014, arXiv:1409.4372], § 7 as well), and K_{\ast }^{MW}(k)$K_{\ast }^{MW}(k)$ is the Milnor–Witt K$K$-theory of the base field k$k$.

We study the renormalized volume of asymptotically hyperbolic Einstein (AHE in short) manifolds 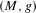(M,g)$(M,g)$ when the conformal boundary 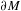\unicode[STIX]{x2202}M$\unicode[STIX]{x2202}M$ has dimension n$n$ even. Its definition depends on the choice of metric 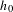h_{0}$h_{0}$ on 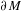\unicode[STIX]{x2202}M$\unicode[STIX]{x2202}M$ in the conformal class at infinity determined by g$g$, we denote it by 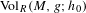\text{Vol}_{R}(M,g;h_{0})$\text{Vol}_{R}(M,g;h_{0})$. We show that 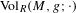\text{Vol}_{R}(M,g;\cdot )$\text{Vol}_{R}(M,g;\cdot )$ is a functional admitting a ‘Polyakov type’ formula in the conformal class 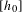[h_{0}]$[h_{0}]$ and we describe the critical points as solutions of some non-linear equation 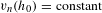v_{n}(h_{0})=\text{constant}$v_{n}(h_{0})=\text{constant}$, satisfied in particular by Einstein metrics. When 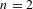n=2$n=2$, choosing extremizers in the conformal class amounts to uniformizing the surface, while if 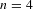n=4$n=4$ this amounts to solving the 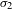\unicode[STIX]{x1D70E}_{2}$\unicode[STIX]{x1D70E}_{2}$-Yamabe problem. Next, we consider the variation of 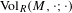\text{Vol}_{R}(M,\cdot ;\cdot )$\text{Vol}_{R}(M,\cdot ;\cdot )$ along a curve of AHE metrics 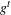g^{t}$g^{t}$ with boundary metric 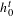h_{0}^{t}$h_{0}^{t}$ and we use this to show that, provided conformal classes can be (locally) parametrized by metrics 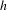h$h$ solving 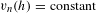v_{n}(h)=\text{constant}$v_{n}(h)=\text{constant}$ and 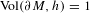\text{Vol}(\unicode[STIX]{x2202}M,h)=1$\text{Vol}(\unicode[STIX]{x2202}M,h)=1$, the set of ends of AHE manifolds (up to diffeomorphisms isotopic to the identity) can be viewed as a Lagrangian submanifold in the cotangent space to the space 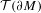{\mathcal{T}}(\unicode[STIX]{x2202}M)${\mathcal{T}}(\unicode[STIX]{x2202}M)$ of conformal structures on 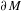\unicode[STIX]{x2202}M$\unicode[STIX]{x2202}M$. We obtain, as a consequence, a higher-dimensional version of McMullen’s quasi-Fuchsian reciprocity. We finally show that conformal classes admitting negatively curved Einstein metrics are local minima for the renormalized volume for a warped product type filling.

A classical article by Misiurewicz and Ziemian (J. Lond. Math. Soc.40(2) (1989), 490–506) classifies the elements in Homeo_{0}(\mathbf{T}^{2})$_{0}(\mathbf{T}^{2})$ by their rotation set \unicode[STIX]{x1D70C}$\unicode[STIX]{x1D70C}$, according to wether \unicode[STIX]{x1D70C}$\unicode[STIX]{x1D70C}$ is a point, a segment or a set with nonempty interior. A recent classification of nonwandering elements in Homeo_{0}(\mathbf{T}^{2})$_{0}(\mathbf{T}^{2})$ by Koropecki and Tal was given in (Invent. Math.196 (2014), 339–381), according to the intrinsic underlying ambient space where the dynamics takes place: planar, annular and strictly toral maps. We study the link between these two classifications, showing that, even abroad the nonwandering setting, annular maps are characterized by rotation sets which are rational segments. Also, we obtain information on the sublinear diffusion of orbits in the—not very well understood—case that \unicode[STIX]{x1D70C}$\unicode[STIX]{x1D70C}$ has nonempty interior.