Article contents
WKB EXPANSIONS FOR HYPERBOLIC BOUNDARY VALUE PROBLEMS IN A STRIP: SELFINTERACTION MEETS STRONG WELL-POSEDNESS
Published online by Cambridge University Press: 29 November 2018
Abstract
In this article we are interested in the rigorous construction of WKB expansions for hyperbolic boundary value problems in the strip 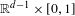 $\mathbb{R}^{d-1}\times [0,1]$. In this geometry, a new inversibility condition has to be imposed to construct the WKB expansion. This new condition is due to selfinteraction phenomenon which naturally appear when several boundary conditions are imposed. More precisely, by selfinteraction we mean that some rays can regenerated themselves after some rebounds against the sides of the strip. This phenomenon is not new and has already been studied in Benoit (Geometric optics expansions for hyperbolic corner problems, I: self-interaction phenomenon, Anal. PDE9(6) (2016), 1359–1418), Sarason and Smoller (Geometrical optics and the corner problem, Arch. Rat. Mech. Anal.56 (1974/75), 34–69) in the corner geometry. In this framework the existence of such selfinteracting rays is linked to specific geometries of the characteristic variety and may seem to be somewhat anecdotal. However for the strip geometry such rays become generic. The new inversibility condition, used to construct the WKB expansion, is a microlocalized version of the one characterizing the uniform in time strong well-posedness (Benoit, Lower exponential strong well-posedness of hyperbolic boundary value problems in a strip (preprint)). It is interesting to point here that such a situation already occurs in the half space geometry (Kreiss, Initial boundary value problems for hyperbolic systems, Comm. Pure Appl. Math.23 (1970), 277–298).
$\mathbb{R}^{d-1}\times [0,1]$. In this geometry, a new inversibility condition has to be imposed to construct the WKB expansion. This new condition is due to selfinteraction phenomenon which naturally appear when several boundary conditions are imposed. More precisely, by selfinteraction we mean that some rays can regenerated themselves after some rebounds against the sides of the strip. This phenomenon is not new and has already been studied in Benoit (Geometric optics expansions for hyperbolic corner problems, I: self-interaction phenomenon, Anal. PDE9(6) (2016), 1359–1418), Sarason and Smoller (Geometrical optics and the corner problem, Arch. Rat. Mech. Anal.56 (1974/75), 34–69) in the corner geometry. In this framework the existence of such selfinteracting rays is linked to specific geometries of the characteristic variety and may seem to be somewhat anecdotal. However for the strip geometry such rays become generic. The new inversibility condition, used to construct the WKB expansion, is a microlocalized version of the one characterizing the uniform in time strong well-posedness (Benoit, Lower exponential strong well-posedness of hyperbolic boundary value problems in a strip (preprint)). It is interesting to point here that such a situation already occurs in the half space geometry (Kreiss, Initial boundary value problems for hyperbolic systems, Comm. Pure Appl. Math.23 (1970), 277–298).
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1629 - 1675
- Copyright
- © Cambridge University Press 2018
References
- 3
- Cited by



