Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-18T10:17:24.032Z Has data issue: false hasContentIssue false
  • English
  • Français

WHITTAKER PERIODS, MOTIVIC PERIODS, AND SPECIAL VALUES OF TENSOR PRODUCT $L$-FUNCTIONS

Part of: Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  31 March 2015

Harald Grobner  and
Michael Harris
Harald Grobner
Affiliation:
Fakultät für Mathematik, Universität Wien, Oskar–Morgenstern–Platz 1, A-1090 Wien, Austria ([email protected])
Michael Harris
Affiliation:
Univ Paris Diderot, Sorbonne Paris Cité, UMR 7586, Institut de Mathématiques de Jussieu-Paris Rive Gauche, Case 247, 4 place Jussieu F-75005, Paris, France Sorbonne Universités, UPMC Univ Paris 06, UMR 7586, IMJ-PRG, F-75005 Paris, France CNRS, UMR7586, IMJ-PRG, F-75013 Paris, France Department of Mathematics, Columbia University, New York, NY 10027, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 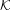${\mathcal{K}}$ be an imaginary quadratic field. Let 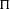${\rm\Pi}$ and 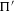${\rm\Pi}^{\prime }$ be irreducible generic cohomological automorphic representation of 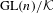$\text{GL}(n)/{\mathcal{K}}$ and 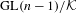$\text{GL}(n-1)/{\mathcal{K}}$, respectively. Each of them can be given two natural rational structures over number fields. One is defined by the rational structure on topological cohomology, and the other is given in terms of the Whittaker model. The ratio between these rational structures is called a Whittaker period. An argument presented by Mahnkopf and Raghuram shows that, at least if 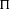${\rm\Pi}$ is cuspidal and the weights of 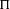${\rm\Pi}$ and 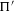${\rm\Pi}^{\prime }$ are in a standard relative position, the critical values of the Rankin–Selberg product 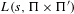$L(s,{\rm\Pi}\times {\rm\Pi}^{\prime })$ are essentially algebraic multiples of the product of the Whittaker periods of 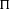${\rm\Pi}$ and 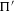${\rm\Pi}^{\prime }$. We show that, under certain regularity and polarization hypotheses, the Whittaker period of a cuspidal 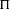${\rm\Pi}$ can be given a motivic interpretation, and can also be related to a critical value of the adjoint $L$-function of related automorphic representations of unitary groups. The resulting expressions for critical values of the Rankin–Selberg and adjoint $L$-functions are compatible with Deligne’s conjecture.

Keywords

cuspidal automorphic representationDeligne’s conjecturespecial valuesL-functionperiodsrationality

MSC classification

Primary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Secondary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F75: Cohomology of arithmetic groups 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 4 , October 2016 , pp. 711 - 769
Copyright
© Cambridge University Press 2015 

References

Ash, A., Non-square-integrable cohomology classes of arithmetic groups, Duke J. Math. 47 (1980), 435–449.Google Scholar
Beuzart-Plessis, R., La conjecture locale de Gross–Prasad pour les représentations tempérées des groupes unitaires, Preprint, 2012, arXiv:1205.2987v2.Google Scholar
Borel, A. and Serre, J.-P., Corners and arithmetic groups, Comm. Math. Helvet. 48 (1973), 436–491.CrossRefGoogle Scholar
Caraiani, A., Local-global compatibility and the action of monodromy on nearby cycles, Duke Math. J. 161 (2012), 2311–2413.CrossRefGoogle Scholar
Clozel, L., Motifs et Formes Automorphes: Applications du Principe de Fonctorialité, in Automorphic Forms, Shimura Varieties, and L-Functions, Vol. I, Ann Arbor, MI, 1988 (ed. Clozel, L. and Milne, J. S.), Perspectives in Mathematics, Volume 10, pp. 77–159 (Academic Press, Boston, MA, 1990).Google Scholar
Clozel, L., Harris, M. and Labesse, J.-P., Construction of automorphic Galois representations, I, in The Stable Trace Formula, Shimura Varieties, and Arithmetic Applications. Volume I: Stabilization of the Trace Formula (ed. Clozel, L. et al. ), pp. 497–527 (International Press, Boston, 2011).Google Scholar
Cogdell, J. W. and Piatetski-Shapiro, I. I. , Remarks on Rankin–Selberg convolutions, in Contributions to Automorphic Forms, Geometry, and Number Theory (ed. Hida, H., Ramakrishnan, D. and Shahidi, F. ), pp. 255–278 (Johns Hopkins University Press, Baltimore, 2004).Google Scholar
Deligne, P., Valeurs de fonctions L et périodes d’intégrales, with an appendix by N. Koblitz and A. Ogus, in Proc. Sympos. Pure Math., Volume XXXIII, part II, pp. 313–346 (American Mathematical Society, Providence, RI, 1979).Google Scholar
Franke, J., Harmonic analysis in weighted L 2 -spaces, Ann. Sci. Éc. Norm. Supér. (4) 31 2 (1998), 181–279.CrossRefGoogle Scholar
Franke, J. and Schwermer, J., A decomposition of spaces of automorphic forms, and the Eisenstein cohomology of arithmetic groups, Math. Ann. 311 (1998), 765–790.CrossRefGoogle Scholar
Goodman, R. and Wallach, N., Symmetry, Representations, and Invariants, Graduate Texts in Mathematics, volume 255 (Springer, Dordrecht, 2009).CrossRefGoogle Scholar
Gordon, J., Transfer to characteristic zero: Appendix to [ 49 ], Duke Math. J. 156 (2011), 220–227.Google Scholar
Grobner, H., Residues of Eisenstein series and the automorphic cohomology of reductive groups, Compos. Math. 149 (2013), 1061–1090.CrossRefGoogle Scholar
Grobner, H., Harris, M. and Lapid, E., Whittaker rational structures and special values of the Asai $L$ -function, Contemp. Math. to appear.Google Scholar
Grobner, H. and Raghuram, A., On some arithmetic properties of automorphic forms of GL m over a division algebra, Int. J. Number Theory 10 (2014), 963–1013.CrossRefGoogle Scholar
Grobner, H. and Raghuram, A., On the arithmetic of Shalika models and the critical values of L-functions for GL2n , with an appendix by Wee Teck Gan, Amer. J. Math. 136 (2014), 675–728.CrossRefGoogle Scholar
Harder, G., Some results on the Eisenstein cohomology of arithmetic subgroups of GL n , in Cohomology of Arithmetic Groups and Automorphic Forms (ed. Labesse, J.-P. and Schwermer, J.), Lecture Notes in Mathematics, Volume 1447, pp. 85–153 (Springer, 1990).CrossRefGoogle Scholar
Harder, G. and Raghuram, A., Eisenstein cohomology for $\text{GL}_{N}$ and ratios of critical values of Rankin–Selberg $L$ -functions - I, manuscript (2014).Google Scholar
Harris, R. N., The refined Gross–Prasad conjecture for unitary groups, Compos. Math. (to appear).Google Scholar
Harris, M., L-functions and periods of polarized regular motives, J. Reine Angew. Math. 483 (1997), 75–161.Google Scholar
Harris, M., A simple proof of rationality of Siegel–Weil Eisenstein series, in Eisenstein Series and Applications (ed. Gan, W. T., Kudla, S. S. and Tschinkel, Y.), Progress in Mathematics, Volume 258, pp. 149–186 (Birkhäuser Boston, Boston, 2008).CrossRefGoogle Scholar
Harris, M., Cohomological automorphic forms on unitary groups, II: period relations and values of L-functions, in Harmonic Analysis, Group Representations, Automorphic Forms and Invariant Theory, Vol. 12 (ed. Li, J.-S. et al. ), Lecture Notes Series, pp. 89–150 (Institute of Mathematical Sciences, National University of Singapore, 2007).CrossRefGoogle Scholar
Harris, M., L-functions and periods of adjoint motives, Algebra Number Theory 7 (2013), 117–155.CrossRefGoogle Scholar
Harris, M. and Labesse, J.-P. , Conditional base change for unitary groups, Asian J. Math. 8 (2004), 653–683.CrossRefGoogle Scholar
Ichino, A. and Yamana, S. , Periods of automorphic forms: the case of (GL n+1 × GL n , GL n ), Compos. Math. (in press).Google Scholar
Ichino, A. and Zhang, W. , Spherical characters for a strongly tempered pair, appendix to [ 50 ].Google Scholar
Jacquet, H., Piatetski-Shapiro, I. I. and Shalika, J., Conducteur des représentations du groupe linéaire, Math. Ann. 256 (1981), 199–214.CrossRefGoogle Scholar
Jacquet, H., Piatetski-Shapiro, I. I. and Shalika, J., Rankin–Selberg convolutions, Amer. J. Math. 105 (1983), 367–464.CrossRefGoogle Scholar
Jacquet, H. and Shalika, J., The Whittaker models of induced representations, Pacific J. Math. 109 (1983), 107–120.CrossRefGoogle Scholar
Kaletha, T., Minguez, A., Shin, S. W. and White, P.-J., Endoscopic classification of representations: inner forms of unitary groups, Preprint, 2014, arXiv:1409.3731.Google Scholar
Labesse, J.-P., Changement de base CM et séries discrètes, in On the Stabilization of the Trace Formula, Vol. I (ed. Clozel, L., Harris, M., Labesse, J.-P. and Ngô, B.-C.), pp. 429–470 (International Press, Boston, MA, 2011).Google Scholar
Li, J.-S. and Schwermer, J., On the Eisenstein cohomology of arithmetic groups, Duke Math. J. 123 (2004), 141–169.CrossRefGoogle Scholar
Jie, L., Period relations for automorphic induction and applications, I, manuscript, Comptes Rendus Math. 353 (2015), 95–100.Google Scholar
Mahnkopf, J., Cohomology of arithmetic groups, parabolic subgroups and the special values of automorphic L-Functions on GL(n), J. Inst. Math. Jussieu 4 (2005), 553–637.CrossRefGoogle Scholar
Mahnkopf, J., Modular symbols and values of L-functions on GL3 , J. Reine Angew. Math. 497 (1998), 91–112.CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L., Spectral Decomposition and Eisenstein Series (Cambridge University Press, 1995).CrossRefGoogle Scholar
Mok, Ch. P., Endoscopic classification of representations of quasi-split unitary groups, Mem. Amer. Math. Soc. 235(1108) (in press).Google Scholar
Raghuram, A., Critical values of Rankin–Selberg $L$ -functions for $\text{GL}_{n}\times \text{GL}_{n-1}$ and the symmetric cube $L$ -functions for $\text{GL}_{2}$ . With an appendix by Chandrasheel Bhagwat, Preprint, 2014.Google Scholar
Raghuram, A., On the special values of certain Rankin–Selberg L-functions and applications to odd symmetric power L-functions of modular forms, Int. Math. Res. Not. IMRN 2010(2) (2009), 334–372.CrossRefGoogle Scholar
Raghuram, A. and Shahidi, F., On certain period relations for cusp forms on $\text{GL}_{n}$ , Int. Math. Res. Not. IMRN (2008), doi:10.1093/imrn/rnn077.CrossRefGoogle Scholar
Rohlfs, J., Projective limits of locally symmetric spaces and cohomology, J. Reine Angew. Math. 479 (1996), 149–182.CrossRefGoogle Scholar
Shahidi, F., Eisenstein Series and Automorphic L-Functions, Colloquium Publications, Volume 58 (American Mathematical Society, 2010).CrossRefGoogle Scholar
Schwermer, J., Kohomologie arithmetisch definierter Gruppen und Eisensteinreihen, Lecture Notes in Mathematics, Volume 988 (Springer-Verlag, 1983).CrossRefGoogle Scholar
Sun, B., The nonvanishing hypothesis at infinity for Rankin–Selberg convolutions, Preprint, 2013, arXiv:1307.5357.Google Scholar
Urban, E., Formes automorphes cuspidales pour GL(2) sur un corps quadratique imaginaire. Valeurs spéciales de fonction L et congruences, Compos. Math. 99 (1995), 283–324.Google Scholar
Waldspurger, J.-L., Quelques propriétés arithmétiques de certaines formes automorphes sur GL(2), Compos. Math. 54 (1985), 121–171.Google Scholar
Yoshida, H., On a conjecture of Shimura concerning periods of Hilbert modular forms, Amer. J. Math. 117 (1995), 1019–1038.CrossRefGoogle Scholar
Yoshida, H., Motives and Siegel modular forms, Amer. J. Math. 123 (2001), 1171–1197.CrossRefGoogle Scholar
Yun, Z., Duke Math. J. 156 (2011), 167–228.Google Scholar
Zhang, W., Fourier transform and the global Gan–Gross–Prasad conjecture for unitary groups, Ann. of Math. 180 (2014), 971–1049.CrossRefGoogle Scholar
Zhang, W., Automorphic period and the central value of Rankin–Selberg L-function, J. Amer. Math. Soc. 27 (2014), 541–612.CrossRefGoogle Scholar