Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T19:00:30.249Z Has data issue: false hasContentIssue false
  • English
  • Français

WHITTAKER FUNCTIONS AND DEMAZURE CHARACTERS

Part of: Special aspects of infinite or finite groups Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  22 June 2017

Kyu-Hwan Lee ,
Cristian Lenart  and
Dongwen Liu
Kyu-Hwan Lee
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06269, USA ([email protected])
Cristian Lenart
Affiliation:
Department of Mathematics and Statistics, State University of New York at Albany, Albany, NY 12222, USA ([email protected])
Dongwen Liu
Affiliation:
School of Mathematical Science, Zhejiang University, Hangzhou 310027, Zhejiang, PR China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider how to express an Iwahori–Whittaker function through Demazure characters. Under some interesting combinatorial conditions, we obtain an explicit formula and thereby a generalization of the Casselman–Shalika formula. Under the same conditions, we compute the transition matrix between two natural bases for the space of Iwahori fixed vectors of an induced representation of a 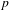$p$-adic group; this corrects a result of Bump–Nakasuji.

Keywords

Iwahori–Whittaker functionsCasselman–Shalika formulaDemazure charactersDemazure–Lusztig operatorsshellability

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields 20F55: Reflection and Coxeter groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 4 , July 2019 , pp. 759 - 781
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

K.-H.L. was partially supported by a grant from the Simons Foundation (#318706). C.L. was partially supported by the NSF grant DMS–1362627. D.L. was partially supported by the Fundamental Research Funds for the Central Universities 2016QNA3002.

References

Billey, S. and Lakshmibai, V., Singular Loci of Schubert Varieties, Progress in Mathematics, 182, (Birkhäuser Boston Inc., Boston, MA, 2000).Google Scholar
Björner, A. and Wachs, M., Bruhat order of Coxeter groups and shellability, Adv. Math. 43 (1982), 87–100.Google Scholar
Brubaker, B., Bump, D. and Licata, A., Whittaker functions and Demazure operators, J. Number Theory 146 (2015), 41–68.Google Scholar
Bump, D. and Nakasuji, M., Casselman’s basis of Iwahori vectors and the Bruhat order, Canad. J. Math. 63 (2011), 1238–1253.Google Scholar
Casselman, W., The unramified principal series of p-adic groups I. The spherical function, Compos. Math. 40 (1980), 387–406.Google Scholar
Casselman, W. and Shalika, J., The unramified principal series of p-adic groups II. The Whittaker function, Compos. Math. 41 (1980), 207–231.Google Scholar
Deodhar, V. V., Some characterizations of Bruhat ordering on a Coxeter group and determination of the relative Möbius function, Invent. Math. 39 (1977), 187–198.Google Scholar
Deodhar, V. V., A combinatorial setting for questions in Kazhdan–Lusztig theory, Geom. Dedicata 36 (1990), 95–119.Google Scholar
Lenart, C. and Zainoulline, K., Towards generalized cohomology Schubert calculus via formal root polynomials, Math. Res. Lett. (2014), Preprint, arXiv:1408.5952 (to appear).Google Scholar
Nakasuji, M. and Naruse, H., Yang-Baxter basis of Hecke algebra and Casselman’s problem (extended abstract), in Proceedings of FPSAC 2016, Discrete Math. Theor, Comput. Sci. Proc., pp. 935–946 (Assoc. Discrete Math. Theor. Comput. Sci., Nancy, 2016).Google Scholar