Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T17:51:43.315Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIÉTÉS DE KISIN STRATIFIÉES ET DÉFORMATIONS POTENTIELLEMENT BARSOTTI-TATE

Published online by Cambridge University Press:  08 September 2016

Xavier Caruso ,
Agnès David  and
Ariane Mézard
Xavier Caruso
Affiliation:
IRMAR, Université de Rennes 1, UMR 6625, Campus de Beaulieu, 35042 Rennes Cedex, France ([email protected])
Agnès David
Affiliation:
Laboratoire de Mathématiques de Besançon, UMR 6623, Université de Franche-Comté, 16 route de Gray, 25030 Besançon Cedex, France ([email protected])
Ariane Mézard
Affiliation:
Institut de Mathématiques de Jussieu Paris Rive-Gauche, UMR 7586, LabEx SMP Université Pierre et Marie Curie, 75005 Paris, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $F$ be a unramified finite extension of 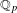$\mathbb{Q}_{p}$ and 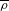$\overline{\unicode[STIX]{x1D70C}}$ be an irreducible mod $p$ two-dimensional representation of the absolute Galois group of $F$. The aim of this article is the explicit computation of the Kisin variety parameterizing the Breuil–Kisin modules associated to certain families of potentially Barsotti–Tate deformations of 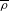$\overline{\unicode[STIX]{x1D70C}}$. We prove that this variety is a finite union of products of 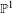$\mathbb{P}^{1}$. Moreover, it appears as an explicit closed connected subvariety of 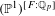$(\mathbb{P}^{1})^{[F:\mathbb{Q}_{p}]}$. We define a stratification of the Kisin variety by locally closed subschemes and explain how the Kisin variety equipped with its stratification may help in determining the ring of Barsotti–Tate deformations of 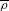$\overline{\unicode[STIX]{x1D70C}}$.

Soient $F$ une extension finie non ramifiée de 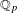$\mathbb{Q}_{p}$ et $\overline{\unicode[STIX]{x1D70C}}$ une représentation modulo 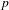$p$ irréductible de dimension 2 du groupe de Galois absolu de $F$. L’objet de ce travail est la détermination de la variété de Kisin qui paramètre les modules de Breuil-Kisin associés à certaines familles de déformations potentiellement Barsotti-Tate de 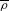$\overline{\unicode[STIX]{x1D70C}}$. Nous démontrons que cette variété est une réunion finie de produits de 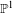$\mathbb{P}^{1}$ qui s’identifie à une sous-variété explicite connexe de 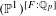$(\mathbb{P}^{1})^{[F:\mathbb{Q}_{p}]}$. Nous définissons une stratification de la variété de Kisin en sous-schémas localement fermés et expliquons enfin comment la variété de Kisin ainsi stratifiée peut aider à déterminer l’anneau des déformations potentiellement Barsotti-Tate de 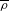$\overline{\unicode[STIX]{x1D70C}}$.

Keywords

p-adic Hodge theoryGalois representationsdeformationsBreuil–Kisin modulesKisin variety
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 5 , November 2018 , pp. 1019 - 1064
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

Breuil, C., Sur un problème de compatibilité local-global modulo p pour GL2 (avec un appendice de L. Dembélé), J. Reine Angew. Math. 692 (2014), 1–76.Google Scholar
Breuil, C. et Mézard, A., Multiplicités modulaires raffinées, Bull. Soc. Math. France 142 (2014), 127–175.Google Scholar
Caruso, X., Représentations galoisiennes p-adiques et (𝜑, 𝜏)-modules, Duke Math. J. 162(13) (2013), 2525–2607.Google Scholar
Caruso, X., Estimation des dimensions de certaines variétés de Kisin, J. Reine Angew. Math. (2015), doi:10.1515/crelle-2014-0066.Google Scholar
Caruso, X., David, A. et Mézard, A., Calculs d’anneaux de déformations potentiellement Barsotti-Tate, À paraître aux Trans. Amer. Math. Soc.Google Scholar
Caruso, X. et Liu, T., Quasi semistable representations, Bull. Soc. Math. France 137 (2009), 185–223.Google Scholar
De Jong, A. J., Crystalline Dieudonné module theory via formal and rigid geometry, Publ. Math. Inst. Hautes Études Sci. 82 (1995), 5–96.Google Scholar
Emerton, M. et Gee, T., A geometric perspective on the Breuil–Mézard conjecture, J. Math. Jussieu 13 (2014), 183–223.Google Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux I, in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87, pp. 249–309 (Birkhäuser Boston, Boston, MA, 1990).Google Scholar
Fontaine, J.-M., Représentations ℓ-adiques potentiellement semi-stables, Astérisque 223 (1994), 321–347.Google Scholar
Hellmann, E., On the structure of some moduli spaces of finite flat group schemes, Mosc. Math. J. 9 (2009), 531–561.Google Scholar
Hellmann, E., Connectedness of Kisin’s varieties for GL2 , Adv. Math. 228 (2011), 219–240.Google Scholar
Imai, N., Finite flat models of constant group schemes of rank two, Proc. Amer. Math. Soc. 138 (2010), 3827–3833.Google Scholar
Imai, N., Ramification and moduli spaces of finite flat models, Ann. Inst. Fourier 61 (2011), 1943–1975.Google Scholar
Kisin, M., Crystalline representations and F-crystals, Progr. Math. 253 (2006), 459–496.Google Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21(2) (2008), 513–546.Google Scholar
Kisin, M., Moduli of finite flat group schemes and modularity, Ann. of Math. (2) 107 (2009), 1085–1180.Google Scholar
Kisin, M., The structure of potentially semi-stable deformation rings, in Actes du Congrès International des Mathématiciens, Vol. II, pp. 294–311. (2010).Google Scholar
Mazur, B., Deforming Galois representations, in Galois Groups Over ℚ (Berkeley CA, 1987), Volume 16, pp. 395–437 (Math. Sci. Res. Inst. Publ., 1989).Google Scholar
Pappas, G. et Rapoport, M., 𝛷-modules and coefficient spaces, Mosc. Math. J. 9 (2009), 625–663.Google Scholar
Wintenberger, J.-P., Le corps des normes de certaines extensions infinies de corps locaux; applications, Ann. Sci. Éc. Norm. Supér. (4) 16 (1983), 59–89.Google Scholar