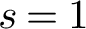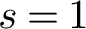1 Introduction and statement of results
Let V be a connected regular scheme with
![]() $V \to \mathrm {Spec}~\mathbb Z$
flat projective and consider its scheme zeta function
$V \to \mathrm {Spec}~\mathbb Z$
flat projective and consider its scheme zeta function
 $$ \begin{align*}\zeta(V,s) = \prod_{x \in V} \frac{1}{(1-N(x)^{-s})};\end{align*} $$
$$ \begin{align*}\zeta(V,s) = \prod_{x \in V} \frac{1}{(1-N(x)^{-s})};\end{align*} $$
the product is over all closed points x of V and
![]() $N(x)$
is the size of the finite residue field of x. The first author [Reference Lichtenbaum27, Conjecture 3.1] has recently conjectured a formula for the special value
$N(x)$
is the size of the finite residue field of x. The first author [Reference Lichtenbaum27, Conjecture 3.1] has recently conjectured a formula for the special value
![]() $\zeta ^{*}(V,r)$
as a generalised Euler characteristic (up to powers of 2):
$\zeta ^{*}(V,r)$
as a generalised Euler characteristic (up to powers of 2):
The basic example is the case when
![]() $V = \mathrm {Spec}~\mathcal O_{F}$
where
$V = \mathrm {Spec}~\mathcal O_{F}$
where
![]() $\mathcal O_{F}$
is the ring of integers of a number field F; then (1) recovers [Reference Lichtenbaum27, §7] the well-known class number formula (15) for
$\mathcal O_{F}$
is the ring of integers of a number field F; then (1) recovers [Reference Lichtenbaum27, §7] the well-known class number formula (15) for
![]() $r=0$
and
$r=0$
and
![]() $r=1$
(see Subsection 2.7) and, for
$r=1$
(see Subsection 2.7) and, for
![]() $r\neq 0,1$
, the formula (1) recovers the conjecture [Reference Lichtenbaum25] of the first-named author relating
$r\neq 0,1$
, the formula (1) recovers the conjecture [Reference Lichtenbaum25] of the first-named author relating
![]() $\zeta ^{*}(V,r)$
and algebraic K-theory. The next case of interest would be that of arithmetic surfaces and
$\zeta ^{*}(V,r)$
and algebraic K-theory. The next case of interest would be that of arithmetic surfaces and
![]() $r=1$
(considered in this article). The compatibility of (1) with the functional equation, proved in [Reference Lichtenbaum27, §6] using the deep results of Bloch–Kato–Saito [Reference Kato and Saito22], is a strong point in support of the conjecture. Our results for arithmetic surfaces provide additional evidence for (1).
$r=1$
(considered in this article). The compatibility of (1) with the functional equation, proved in [Reference Lichtenbaum27, §6] using the deep results of Bloch–Kato–Saito [Reference Kato and Saito22], is a strong point in support of the conjecture. Our results for arithmetic surfaces provide additional evidence for (1).
1.1 History
It is a fascinating and important problem to give a description of these special values in terms of cohomological invariants of V. The first conjectural attempt at such a description was given in 1991 by Fontaine and Perrin-Riou [Reference Fontaine and Perrin-Riou16, Reference Fontaine15], building on previous work by Deligne, Beilinson, Bloch and Kato. Roughly speaking, Bloch and Kato [Reference Bloch and Kato2] considered values at positive integers, while Deligne and Beilinson considered values at negative integers. Fontaine and Perrin-Riou were the first to give a uniform approach valid for all integers.
The reader should be warned that the conjectures of Fontaine and Perrin-Riou [Reference Fontaine and Perrin-Riou16, Reference Fontaine15] do not in fact concern the scheme zeta function
![]() $\zeta (V,s)$
above but rather the Hasse–Weil zeta function
$\zeta (V,s)$
above but rather the Hasse–Weil zeta function
![]() $\zeta _{HW}(V_{0},s)$
, which is the alternating product of Hasse–Weil L-functions
$\zeta _{HW}(V_{0},s)$
, which is the alternating product of Hasse–Weil L-functions
![]() $L_{HW}(h^{j}(V_{0}), s)$
[Reference Serre35]. These L-functions
$L_{HW}(h^{j}(V_{0}), s)$
[Reference Serre35]. These L-functions
![]() $L_{HW}(h^{j}(V_{0}), s)$
only depend on the generic fibre
$L_{HW}(h^{j}(V_{0}), s)$
only depend on the generic fibre
![]() $V_{0}$
of
$V_{0}$
of
![]() $V \to \mathrm {Spec}~ \mathbb Z$
, while
$V \to \mathrm {Spec}~ \mathbb Z$
, while
![]() $\zeta (V,s)$
depends on the special fibres as well. In fact, Fontaine and Perrin-Riou gave conjectures for the special values of the L-functions
$\zeta (V,s)$
depends on the special fibres as well. In fact, Fontaine and Perrin-Riou gave conjectures for the special values of the L-functions
![]() $L_{HW}(h^{j}(V_{0}), s)$
, whose alternating product yields conjectures for the Hasse–Weil zeta function
$L_{HW}(h^{j}(V_{0}), s)$
, whose alternating product yields conjectures for the Hasse–Weil zeta function
 $\zeta _{HW}(V_{0}, s)= \prod _{j} (L_{HW}(h^{j}(V_{0}), s))^{(-1)^{j+1}}$
. These two zeta functions agree if V is smooth over Spec
$\zeta _{HW}(V_{0}, s)= \prod _{j} (L_{HW}(h^{j}(V_{0}), s))^{(-1)^{j+1}}$
. These two zeta functions agree if V is smooth over Spec
![]() $\Bbb Z$
but not in general.
$\Bbb Z$
but not in general.
Fontaine and Perrin-Riou first introduced various (conjecturally) finite-dimensional vector spaces and made a conjecture (which we will call Conjecture FPR) giving the special value of the (Hasse–Weil) zeta function
![]() $\zeta _{HW}(V_{0}, s)$
up to a rational number in terms of determinants of maps between these vector spaces tensored with
$\zeta _{HW}(V_{0}, s)$
up to a rational number in terms of determinants of maps between these vector spaces tensored with
![]() $\Bbb R$
. They then used spaces taken from p-adic Hodge theory to refine these conjectures to obtain a conjecture for the special value of
$\Bbb R$
. They then used spaces taken from p-adic Hodge theory to refine these conjectures to obtain a conjecture for the special value of
![]() $\zeta _{HW}(V_{0}, s)$
up to sign.
$\zeta _{HW}(V_{0}, s)$
up to sign.
A crude description of the main conjecture made in 2017 by the first author [Reference Lichtenbaum27] (which we will call Conjecture L) would be to say that it refines Conjecture FPR by using canonical integral models for the vector spaces used in that conjecture, avoiding the necessity for p-adic Hodge theory. In fact, the difference between the scheme zeta function and the Hasse–Weil zeta function forces minor changes in the vector spaces to be considered. These changes are similar to those made in [Reference Flach and Morin12] for the same reason. In 2016, Flach and Morin [Reference Flach and Morin12] also made a general special values conjecture, which we will refer to as Conjecture FM1. Conjecture FM1 does make use of p-adic Hodge theory and is more closely related to Conjecture FPR than is Conjecture L. In fact, Conjecture FM1 can be shown to be equivalent to Conjecture FPR if V is smooth over Spec
![]() $\Bbb Z$
; see [Reference Flach and Morin12].
$\Bbb Z$
; see [Reference Flach and Morin12].
In 2019, Flach and Morin [Reference Flach and Morin13] made a new conjecture (referred to here as Conjecture FM2) which avoids p-adic Hodge theory and so is more closely modeled on Conjecture L and less related to Conjecture FPR. In fact, it seems plausible that it is not too difficult to show that Conjecture L is equivalent to Conjecture FM2, except that Conjecture FM2 eliminates the 2-power indeterminacy. Both Conjecture L and Conjecture FM2 have been shown to be compatible [Reference Lichtenbaum27, Reference Flach and Morin13] with a form of the functional equation for the scheme zeta function. This has not been shown for either Conjecture FM1 or Conjecture FPR.
Conjecture L is a bit more ad hoc than Conjecture FM2 but has the advantage that it involves much less elaborate machinery. Of course, as previously mentioned, Conjecture FM2 is more precise, but we hope that is possible to remedy this by modifying Conjecture L using the Artin–Verdier topology.
Conjecture FPR is local: for each prime p, a conjecture is formulated involving sophisticated p-adic Hodge theory and the corresponding local variety
![]() $V \times \mathrm {Spec}~\mathbb Q_{p}$
, and it is their combination (for all primes p) that determines the special value up to sign. In contrast, Conjecture L (and FM2) is truly global as it produces a description of
$V \times \mathrm {Spec}~\mathbb Q_{p}$
, and it is their combination (for all primes p) that determines the special value up to sign. In contrast, Conjecture L (and FM2) is truly global as it produces a description of
![]() $\zeta ^{*}(V,r)$
intrinsically in terms of invariants of V. For instance, in the case of an arithmetic surface X, where Conjecture FPR calculates the order of the Tate–Shafarevich group
$\zeta ^{*}(V,r)$
intrinsically in terms of invariants of V. For instance, in the case of an arithmetic surface X, where Conjecture FPR calculates the order of the Tate–Shafarevich group
![]() of the Jacobian J of the generic fibre
of the Jacobian J of the generic fibre
![]() $X_{0}$
of X, Conjecture L for
$X_{0}$
of X, Conjecture L for
![]() $\zeta ^{*}(X,1)$
concerns its intrinsic counterpart: the Brauer group
$\zeta ^{*}(X,1)$
concerns its intrinsic counterpart: the Brauer group
![]() $\textrm {Br}(X)$
.
$\textrm {Br}(X)$
.
1.2 The conjecture for arithmetic surfaces
Let
![]() $S =\text {Spec}~\mathcal O_{F}$
be the spectrum of the ring of integers
$S =\text {Spec}~\mathcal O_{F}$
be the spectrum of the ring of integers
![]() $\mathcal O_{F}$
in a number field F. In this article, an arithmetic surface X over S will mean
$\mathcal O_{F}$
in a number field F. In this article, an arithmetic surface X over S will mean
-
• a regular scheme X (of dimension 2) together with a projective flat morphism
 $\pi : X \to S$
;
$\pi : X \to S$
; -
• the generic fibre
 $X_{0} \to \text {Spec}~F$
is a geometrically connected smooth projective curve of genus g.
$X_{0} \to \text {Spec}~F$
is a geometrically connected smooth projective curve of genus g.
We recall the conjecture of [Reference Lichtenbaum27, Conjecture 3.1] for the case at hand:
![]() $V=X$
and
$V=X$
and
![]() $r=1$
.
$r=1$
.
Conjecture 1. For an arithmetic surface X as above, the special value of
![]() $\zeta ^{*}(X,1)$
at
$\zeta ^{*}(X,1)$
at
![]() $s=1$
is a generalised Euler characteristic
$s=1$
is a generalised Euler characteristic
![]() $\chi (X,1)$
(up to powers of 2),
$\chi (X,1)$
(up to powers of 2),
 $$ \begin{align*}\zeta^{*}(X,1) = \pm \chi(X,1) = \pm \frac{\chi_{A,C}(X,1)}{\chi_{B}(X,1)} .\end{align*} $$
$$ \begin{align*}\zeta^{*}(X,1) = \pm \chi(X,1) = \pm \frac{\chi_{A,C}(X,1)}{\chi_{B}(X,1)} .\end{align*} $$
As we shall see in Subsection 7.5, this provides a description of
![]() $\zeta ^{*}(X,1)$
in terms of (periods computed using) the finitely generated
$\zeta ^{*}(X,1)$
in terms of (periods computed using) the finitely generated
![]() $\mathcal O_{F}$
-modules
$\mathcal O_{F}$
-modules
![]() $H^{*}(X, \mathcal O)$
, the Betti cohomology
$H^{*}(X, \mathcal O)$
, the Betti cohomology
![]() $H^{*}_{B}(X_{\mathbb C}, \mathbb Z(1))$
, the conjecturally finite group
$H^{*}_{B}(X_{\mathbb C}, \mathbb Z(1))$
, the conjecturally finite group
![]() $\textrm {Br}(X)$
, the finitely generated abelian group
$\textrm {Br}(X)$
, the finitely generated abelian group
![]() $\textrm {Pic}(X)$
and the Arakelov intersection pairing on
$\textrm {Pic}(X)$
and the Arakelov intersection pairing on
![]() $\textrm {Pic}^{0}(X)$
.
$\textrm {Pic}^{0}(X)$
.
Our main result is the following theorem.
Theorem 2. Conjecture 1 is equivalent to the Birch–Swinnerton–Dyer conjecture (Conjecture 20) for the Jacobian J of
![]() $X_{0}$
over F.
$X_{0}$
over F.
Remark 3.
-
(i) This theorem is the analogue (Subsection 7.5) for arithmetic surfaces of Conjecture (d) [Reference Tate36, p. 427]; see [Reference Lichtenbaum26, Reference Gordon18, Reference Liu, Lorenzini and Raynaud30, Reference Liu, Lorenzini and Raynaud32]. Such an arithmetic analogue had long been expected. Flach–Siebel [Reference Flach and Siebel14] proved a similar relation between the conjectures of Flach–Morin [Reference Flach and Morin12] for X and Conjecture 20.
-
(ii) In a certain sense, Conjecture 1 is dual to Conjecture 20. When
 $X_{0}$
is an elliptic curve, the former uses the proper map
$X_{0}$
is an elliptic curve, the former uses the proper map
 $\pi :X\to S$
that may not be smooth, whereas the latter uses the Néron model
$\pi :X\to S$
that may not be smooth, whereas the latter uses the Néron model
 $\mathcal N$
of
$\mathcal N$
of
 $X_{0}$
(and the smooth map
$X_{0}$
(and the smooth map
 $\mathcal N \to S$
may not be proper). This suggests that one should start with the case when
$\mathcal N \to S$
may not be proper). This suggests that one should start with the case when
 $\pi $
is smooth and admits a section; this case is considered in Section 5.
$\pi $
is smooth and admits a section; this case is considered in Section 5. -
(iii) If
 $g=0$
, then J is trivial. Since Conjecture 20 is obviously true in this case, Theorem 2 gives a proof of Conjecture 1 for
$g=0$
, then J is trivial. Since Conjecture 20 is obviously true in this case, Theorem 2 gives a proof of Conjecture 1 for
 $g=0$
. See Remark 43 for details.
$g=0$
. See Remark 43 for details.
Since Tate [Reference Tate36] has proved that Conjecture 20 is invariant under isogeny, one obtains the following.
Corollary 4. Suppose X and
![]() $X^{\prime }$
are arithmetic surfaces over S such that the Jacobians of
$X^{\prime }$
are arithmetic surfaces over S such that the Jacobians of
![]() $X^{\prime }_{0}$
and
$X^{\prime }_{0}$
and
![]() $X_{0}$
are isogenous over F. Then Conjecture 1 for X is equivalent to Conjecture 1 for
$X_{0}$
are isogenous over F. Then Conjecture 1 for X is equivalent to Conjecture 1 for
![]() $X^{\prime }$
.
$X^{\prime }$
.
In particular, Conjecture 1 for (the regular integral models of) an elliptic curve E and a torsor T over E are equivalent.
1.3 Plan of the article
We start in Section 2 with a presentation of the main conjecture from [Reference Lichtenbaum27] and provide a detailed description of the basic examples (
![]() $V=S$
); in particular, we show that the conjecture recovers the analytic class number formula (15). This is followed in Section 3 by the conjecture (Conjecture 20) of Birch–Swinnerton–Dyer (and Tate) for the global L-function of an abelian variety over a number field. Here we rely on [Reference Gross19] because it contains the formulation of Conjecture 20 in terms of Néron models and provides the definition of a period even when the (projective) module of invariant differentials on the Néron model is not free as a
$V=S$
); in particular, we show that the conjecture recovers the analytic class number formula (15). This is followed in Section 3 by the conjecture (Conjecture 20) of Birch–Swinnerton–Dyer (and Tate) for the global L-function of an abelian variety over a number field. Here we rely on [Reference Gross19] because it contains the formulation of Conjecture 20 in terms of Néron models and provides the definition of a period even when the (projective) module of invariant differentials on the Néron model is not free as a
![]() $\mathcal O_{F}$
-module.
$\mathcal O_{F}$
-module.
In Section 4, we prove the key relation (Theorem 23) between the period in Conjecture 20 and the period in Conjecture 1.
Section 5 contains the proof of Theorem 2 in the special but illustrative and important case where
![]() $\pi :X \to S$
is smooth and
$\pi :X \to S$
is smooth and
![]() $X_{0}(F)$
is nonempty. The rich intersection theory on a regular surface figures prominently in Section 6. The beautiful results of Raynaud–Liu–Lorenzini [Reference Liu, Lorenzini and Raynaud30, Reference Bosch and Liu3, Reference Bosch, Lütkebohmert and Raynaud4] on the Néron model, the connected components of the special fibre and the relation to intersection theory play a key role in our article. Though the analysis of the role of torsion in derived de Rham cohomology could complicate the study of
$X_{0}(F)$
is nonempty. The rich intersection theory on a regular surface figures prominently in Section 6. The beautiful results of Raynaud–Liu–Lorenzini [Reference Liu, Lorenzini and Raynaud30, Reference Bosch and Liu3, Reference Bosch, Lütkebohmert and Raynaud4] on the Néron model, the connected components of the special fibre and the relation to intersection theory play a key role in our article. Though the analysis of the role of torsion in derived de Rham cohomology could complicate the study of
![]() $\zeta ^{*}(V,r)$
in general, these results help us bypass the torsion in
$\zeta ^{*}(V,r)$
in general, these results help us bypass the torsion in
![]() $H^{1}(X, \mathcal O_{X})$
. An equally important role is played by the result of Geisser [Reference Geisser17]. Finally, the proof of Theorem 2 is completed in Section 7.
$H^{1}(X, \mathcal O_{X})$
. An equally important role is played by the result of Geisser [Reference Geisser17]. Finally, the proof of Theorem 2 is completed in Section 7.
The concept of integral structures and derived differentials is resonant with the methods used in the study of
![]() $\epsilon $
-constants, Arakelov theory [Reference Chinburg, Erez, Pappas and Taylor5, Reference Chinburg, Pappas and Taylor6] and Bloch’s conjectural formula for the conductor [Reference Kato and Saito22].
$\epsilon $
-constants, Arakelov theory [Reference Chinburg, Erez, Pappas and Taylor5, Reference Chinburg, Pappas and Taylor6] and Bloch’s conjectural formula for the conductor [Reference Kato and Saito22].
Notations
As usual, we write
![]() $d_{F}$
for the discriminant of F over
$d_{F}$
for the discriminant of F over
![]() $\mathbb Q$
, h for the class number of F and w the number of roots of unity in F. Using the notation
$\mathbb Q$
, h for the class number of F and w the number of roots of unity in F. Using the notation
![]() $A_{tor}$
for the torsion subgroup of an abelian group A and
$A_{tor}$
for the torsion subgroup of an abelian group A and
![]() $[B]$
for the cardinality of a finite group B, one has
$[B]$
for the cardinality of a finite group B, one has
![]() $w= [F^{*}_{tor}]$
.
$w= [F^{*}_{tor}]$
.
We shall use S to indicate both Spec
![]() $\mathcal O_{F}$
and the set of nonzero prime ideals of
$\mathcal O_{F}$
and the set of nonzero prime ideals of
![]() $\mathcal O_{F}$
. Thus,
$\mathcal O_{F}$
. Thus,
![]() $v\in S$
means a closed point of S or a nonzero prime ideal in
$v\in S$
means a closed point of S or a nonzero prime ideal in
![]() $\mathcal O_{F}$
. We write
$\mathcal O_{F}$
. We write
![]() $q_{v}$
for the size of the finite residue field
$q_{v}$
for the size of the finite residue field
![]() $k(v)$
.
$k(v)$
.
Let
![]() $\tilde {S}$
denote the set of embeddings of F into
$\tilde {S}$
denote the set of embeddings of F into
![]() $\mathbb C$
; complex conjugation c on
$\mathbb C$
; complex conjugation c on
![]() $\mathbb C$
induces an involution
$\mathbb C$
induces an involution
![]() $\sigma \mapsto c\sigma = \bar {\sigma }$
on
$\sigma \mapsto c\sigma = \bar {\sigma }$
on
![]() $\tilde {S}$
via
$\tilde {S}$
via
The set
![]() $S_{\infty }$
of infinite places of S is the set of orbits of the involution; the set of fixed points of the involution is exactly the subset
$S_{\infty }$
of infinite places of S is the set of orbits of the involution; the set of fixed points of the involution is exactly the subset
![]() $S_{\mathbb R}$
of embeddings of F into
$S_{\mathbb R}$
of embeddings of F into
![]() $\mathbb R$
. As usual,
$\mathbb R$
. As usual,
![]() $r_{1}$
is the size of
$r_{1}$
is the size of
![]() $S_{\mathbb R}$
and
$S_{\mathbb R}$
and
![]() $r {}_{1}+ r_{2}$
is the size of
$r {}_{1}+ r_{2}$
is the size of
![]() $S_{\infty }$
.
$S_{\infty }$
.
For any scheme Y over S, we put
![]() $Y_{\mathbb C} = Y \times _{\mathrm {Spec}~\mathbb Z} \mathrm {Spec}~\mathbb C$
and
$Y_{\mathbb C} = Y \times _{\mathrm {Spec}~\mathbb Z} \mathrm {Spec}~\mathbb C$
and
![]() $Y_{\sigma }$
for the base change along
$Y_{\sigma }$
for the base change along
![]() $\sigma :F \to \mathbb C$
:
$\sigma :F \to \mathbb C$
:

We write
![]() $H^{*}_{et}(Y, \mathbb Z(r))$
for the étale motivic cohomology groups of Y; these are the hypercohomology groups of Bloch’s higher Chow group complex in the étale topology of Y.
$H^{*}_{et}(Y, \mathbb Z(r))$
for the étale motivic cohomology groups of Y; these are the hypercohomology groups of Bloch’s higher Chow group complex in the étale topology of Y.
2 Statement of the main conjecture from [Reference Lichtenbaum27]
Fix a connected regular scheme V of dimension d together with a projective flat morphism
![]() $V \to S$
; we assume that the generic fibre
$V \to S$
; we assume that the generic fibre
![]() $V_{0} \to \mathrm {Spec}~F$
is a geometrically connected smooth variety of dimension
$V_{0} \to \mathrm {Spec}~F$
is a geometrically connected smooth variety of dimension
![]() $d-1$
over Spec F. The aim of this section is to present the conjectural formula from [Reference Lichtenbaum27] for the special value
$d-1$
over Spec F. The aim of this section is to present the conjectural formula from [Reference Lichtenbaum27] for the special value
![]() $\zeta ^{*}(V,r)$
.
$\zeta ^{*}(V,r)$
.
2.1 The Bloch–Kato–Fontaine–Perrin-Riou conjecture [Reference Fontaine15, Reference Fontaine and Perrin-Riou16]
The motive
![]() $M= h^{j}(V_{0})(r)$
has a Betti realisation
$M= h^{j}(V_{0})(r)$
has a Betti realisation
 $H^{j}_{B}(V {}_{\mathbb C}, \mathbb Z(r))$
, a de Rham realisation
$H^{j}_{B}(V {}_{\mathbb C}, \mathbb Z(r))$
, a de Rham realisation
 $H^{j}_{dR} (V_{\mathbb C}, \mathbb C(r))$
, an action of complex conjugation c on
$H^{j}_{dR} (V_{\mathbb C}, \mathbb C(r))$
, an action of complex conjugation c on
 $H^{j}_{B}(V {}_{\mathbb C}, \mathbb Z(0)) = H^{j}_{B}(V_{\mathbb C}, \mathbb Z)$
, a Hodge filtration F on
$H^{j}_{B}(V {}_{\mathbb C}, \mathbb Z(0)) = H^{j}_{B}(V_{\mathbb C}, \mathbb Z)$
, a Hodge filtration F on
 $H^{j}_{dR} (V_{\mathbb C}, \mathbb C(r))$
and a period map
$H^{j}_{dR} (V_{\mathbb C}, \mathbb C(r))$
and a period map
 $$ \begin{align*} \theta_{j,r}: H^{j}(V_{\mathbb C}, \mathbb C(r)) \xrightarrow{\sim} H^{j}_{dR}(V_{\mathbb C}, \mathbb C(r)).\end{align*} $$
$$ \begin{align*} \theta_{j,r}: H^{j}(V_{\mathbb C}, \mathbb C(r)) \xrightarrow{\sim} H^{j}_{dR}(V_{\mathbb C}, \mathbb C(r)).\end{align*} $$
As abelian groups,
 $H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r)) = H^{j}_{B}(V_{\mathbb C}, \mathbb Z)$
and
$H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r)) = H^{j}_{B}(V_{\mathbb C}, \mathbb Z)$
and
 $H^{j}_{B}(V_{\mathbb C}, \mathbb C(r)) = H^{j}_{B}(V_{\mathbb C}, \mathbb C)$
; also,
$H^{j}_{B}(V_{\mathbb C}, \mathbb C(r)) = H^{j}_{B}(V_{\mathbb C}, \mathbb C)$
; also,
 $H^{j}_{B}(V_{\mathbb C}, \mathbb C(r)) =H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))\otimes _{\mathbb Z}\mathbb C$
. The map
$H^{j}_{B}(V_{\mathbb C}, \mathbb C(r)) =H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))\otimes _{\mathbb Z}\mathbb C$
. The map
![]() $\theta _{j,0}$
is the classical period map from
$\theta _{j,0}$
is the classical period map from
 $H^{j}_{B}(V_{\mathbb C}, \mathbb C)$
to
$H^{j}_{B}(V_{\mathbb C}, \mathbb C)$
to
 $H^{j}_{dR} (V_{\mathbb C}, \mathbb C)$
. We define
$H^{j}_{dR} (V_{\mathbb C}, \mathbb C)$
. We define
 $$ \begin{align*}H^{j}(V_{\mathbb C}, \mathbb Z(r))^{+} &= \{x \in H^{j}(V_{\mathbb C}, \mathbb Z)~|~ c(x) =~(-1)^{r}\cdot x\}, \\ H^{j}(V_{\mathbb C}, \mathbb C(r))^{+} &= \{x \in H^{j}(V_{\mathbb C}, \mathbb C)~|~ c(x) =~(-1)^{r}\cdot x\}.\end{align*} $$
$$ \begin{align*}H^{j}(V_{\mathbb C}, \mathbb Z(r))^{+} &= \{x \in H^{j}(V_{\mathbb C}, \mathbb Z)~|~ c(x) =~(-1)^{r}\cdot x\}, \\ H^{j}(V_{\mathbb C}, \mathbb C(r))^{+} &= \{x \in H^{j}(V_{\mathbb C}, \mathbb C)~|~ c(x) =~(-1)^{r}\cdot x\}.\end{align*} $$
Finally, the map
![]() $\theta _{j,r}$
defined as
$\theta _{j,r}$
defined as
![]() $(2\pi i)^{r}\cdot \theta _{j,0}$
induces a map
$(2\pi i)^{r}\cdot \theta _{j,0}$
induces a map
 $$ \begin{align} \alpha_{M}: H^{j}(V_{\mathbb C}, \mathbb C(r))^{+} \to M_{B} \xrightarrow{\sim} M_{dR} \to t_{M}= \frac{M_{dR}}{F^{0}}.\end{align} $$
$$ \begin{align} \alpha_{M}: H^{j}(V_{\mathbb C}, \mathbb C(r))^{+} \to M_{B} \xrightarrow{\sim} M_{dR} \to t_{M}= \frac{M_{dR}}{F^{0}}.\end{align} $$
Fontaine–Perrin-Riou [Reference Fontaine and Perrin-Riou16, Reference Fontaine15] introduced certain vector spaces
 $H^{0}_{f}(M)$
and
$H^{0}_{f}(M)$
and
 $H^{1}_{f}(M)$
that are conjecturally finite-dimensional
$H^{1}_{f}(M)$
that are conjecturally finite-dimensional
![]() $\mathbb Q$
-vector spaces. Further, they conjectured the existence of the fundamental exact sequence
$\mathbb Q$
-vector spaces. Further, they conjectured the existence of the fundamental exact sequence
 $$ \begin{align} 0 &\to H^{0}_{f}(M)\otimes{\mathbb R} \xrightarrow{c} \textrm{Ker}(\alpha_{M}) \to H^{1}_{f}(M^{*}(1))^{*}\otimes{\mathbb R} \xrightarrow{h} H^{1}_{f}(M)\otimes{\mathbb R} \xrightarrow{r} \textrm{Coker}(\alpha_{M}) \nonumber \\[3pt] & \to H^{0}_{f}(M^{*}(1))^{*}\otimes{\mathbb R} \to 0, \end{align} $$
$$ \begin{align} 0 &\to H^{0}_{f}(M)\otimes{\mathbb R} \xrightarrow{c} \textrm{Ker}(\alpha_{M}) \to H^{1}_{f}(M^{*}(1))^{*}\otimes{\mathbb R} \xrightarrow{h} H^{1}_{f}(M)\otimes{\mathbb R} \xrightarrow{r} \textrm{Coker}(\alpha_{M}) \nonumber \\[3pt] & \to H^{0}_{f}(M^{*}(1))^{*}\otimes{\mathbb R} \to 0, \end{align} $$
where c is a cycle class map, h is a (Arakelov) height pairing and r is the Beilinson regulator. They used it to reformulate the Deligne–Beilinson conjecture
![]() $C_{DB}(M)$
[Reference Fontaine15] which predicts the special value
$C_{DB}(M)$
[Reference Fontaine15] which predicts the special value
![]() $L^{*}(M,0) \in {\mathbb R^{\times }}/{\mathbb Q^{\times }}$
at
$L^{*}(M,0) \in {\mathbb R^{\times }}/{\mathbb Q^{\times }}$
at
![]() $s=0$
of the L-function
$s=0$
of the L-function
![]() $L(M,s)$
.
$L(M,s)$
.
To predict
![]() $L^{*}(M,0) \in \mathbb R^{\times }$
, they introduced similar exact sequences for each prime p; this is the conjecture
$L^{*}(M,0) \in \mathbb R^{\times }$
, they introduced similar exact sequences for each prime p; this is the conjecture
![]() $C_{BK}(M)$
[Reference Fontaine15] for p. One obtains a prediction for the special value of
$C_{BK}(M)$
[Reference Fontaine15] for p. One obtains a prediction for the special value of
![]() $\zeta _{HW}(V_{0},s)$
at
$\zeta _{HW}(V_{0},s)$
at
![]() $s=r$
by combining
$s=r$
by combining
![]() $C_{BK}(M)$
for the motives
$C_{BK}(M)$
for the motives
![]() $h^{j}(V_{0})(r)$
for all j. For more details, see [Reference Bloch and Kato2, Reference Fontaine and Perrin-Riou16, Reference Kings23, Reference Kings24, Reference Fontaine15, Reference Flach10, Reference Flach11, Reference Flach and Morin12].
$h^{j}(V_{0})(r)$
for all j. For more details, see [Reference Bloch and Kato2, Reference Fontaine and Perrin-Riou16, Reference Kings23, Reference Kings24, Reference Fontaine15, Reference Flach10, Reference Flach11, Reference Flach and Morin12].
But our approach, following [Reference Lichtenbaum27], to
![]() $\zeta ^{*}(V,r)$
is different: we endow the vector spaces in (4) with integral structures using Weil-étale motivic cohomology groups and the de Rham cohomology groups of V. The determinants of the maps in (4) with respect to these integral structures will be used for a description of
$\zeta ^{*}(V,r)$
is different: we endow the vector spaces in (4) with integral structures using Weil-étale motivic cohomology groups and the de Rham cohomology groups of V. The determinants of the maps in (4) with respect to these integral structures will be used for a description of
![]() $\zeta ^{*}(V,r)$
.
$\zeta ^{*}(V,r)$
.
2.2 Weil-étale motivic cohomology groups
These groups
![]() $H^{i}_{W}(V, \mathbb Z(r))$
[Reference Lichtenbaum27, §2.1] are defined as étale motivic cohomology
$H^{i}_{W}(V, \mathbb Z(r))$
[Reference Lichtenbaum27, §2.1] are defined as étale motivic cohomology
![]() $H^{i}_{et}(V, \mathbb Z(r))$
for
$H^{i}_{et}(V, \mathbb Z(r))$
for
![]() $i \le 2r$
and
$i \le 2r$
and
![]() $r \ge 0$
and then, for
$r \ge 0$
and then, for
![]() $i>2r$
, as the dual of étale motivic cohomology
$i>2r$
, as the dual of étale motivic cohomology
thereby, for
![]() $i>2r$
, they sit in an exact sequence
$i>2r$
, they sit in an exact sequence
 $$ \begin{align*}0 \to \textrm{Ext}^{1}(H^{2d+2-i}_{et}(V, \mathbb Z(d-r)), \mathbb Z) \to H^{i}_{W}(V, \mathbb Z(r)) \to \textrm{Hom}(H^{2d+1-i}_{et}(V, \mathbb Z(d-r)), \mathbb Z) \to 0.\end{align*} $$
$$ \begin{align*}0 \to \textrm{Ext}^{1}(H^{2d+2-i}_{et}(V, \mathbb Z(d-r)), \mathbb Z) \to H^{i}_{W}(V, \mathbb Z(r)) \to \textrm{Hom}(H^{2d+1-i}_{et}(V, \mathbb Z(d-r)), \mathbb Z) \to 0.\end{align*} $$
We define
![]() $H^{i}_{W}(X, \mathbb Z(r))$
to be zero when
$H^{i}_{W}(X, \mathbb Z(r))$
to be zero when
![]() $r<0$
and
$r<0$
and
![]() $i\le 2r$
.
$i\le 2r$
.
The groups
![]() $H^{i}_{W}(V, \mathbb Z(r))$
are conjectured to be finitely generated.
$H^{i}_{W}(V, \mathbb Z(r))$
are conjectured to be finitely generated.
2.3 Integral structures and complexes
We recall the well-known theory of determinants [Reference Kings24, Lecture 1, §5].
A lattice L in a finite-dimensional vector space C is the
![]() $\mathbb Z$
-submodule generated by a basis of C. Write
$\mathbb Z$
-submodule generated by a basis of C. Write
![]() $\Lambda L \cong \mathbb Z$
(noncanonically) for the highest exterior power of L and
$\Lambda L \cong \mathbb Z$
(noncanonically) for the highest exterior power of L and
![]() $\Lambda C \cong \mathbb C$
(noncanonically) for the highest exterior power of C and
$\Lambda C \cong \mathbb C$
(noncanonically) for the highest exterior power of C and
![]() $(\Lambda C)^{-1}$
for its dual. Given a finite complex of finite-dimensional complex vector spaces
$(\Lambda C)^{-1}$
for its dual. Given a finite complex of finite-dimensional complex vector spaces
![]() $C_{i}$
and lattices
$C_{i}$
and lattices
![]() $L_{i} \subset C_{i}$
$L_{i} \subset C_{i}$
 $$ \begin{align*}C_{\bullet} :\qquad 0 \to \cdots C_{i} \xrightarrow{f_{i}} C_{i+1} \xrightarrow{f_{i+1}} C_{i+2} \to \cdots, \end{align*} $$
$$ \begin{align*}C_{\bullet} :\qquad 0 \to \cdots C_{i} \xrightarrow{f_{i}} C_{i+1} \xrightarrow{f_{i+1}} C_{i+2} \to \cdots, \end{align*} $$
one has a canonical map
![]() $g: \Lambda (L_{\bullet }) \to \Lambda (C_{\bullet })$
where
$g: \Lambda (L_{\bullet }) \to \Lambda (C_{\bullet })$
where
 $$ \begin{align*} \Lambda (L_{\bullet}) = \otimes_{j}(\Lambda L_{j})^{(-1)^{j}} \cong \mathbb Z, \qquad \Lambda(C_{\bullet}) = \otimes_{i} (\Lambda C_{i})^{(-1)^{i}}.\end{align*} $$
$$ \begin{align*} \Lambda (L_{\bullet}) = \otimes_{j}(\Lambda L_{j})^{(-1)^{j}} \cong \mathbb Z, \qquad \Lambda(C_{\bullet}) = \otimes_{i} (\Lambda C_{i})^{(-1)^{i}}.\end{align*} $$
If
![]() $C_{\bullet }$
is exact, then one has a canonical isomorphism
$C_{\bullet }$
is exact, then one has a canonical isomorphism
We define
as the image of a generator e of
![]() $\Lambda (L_{\bullet }) \cong \mathbb Z$
under the composite map
$\Lambda (L_{\bullet }) \cong \mathbb Z$
under the composite map
 $$ \begin{align*}\Lambda (L_{\bullet}) \xrightarrow{g} \Lambda (C_{\bullet}) \xrightarrow{h} \mathbb C;\end{align*} $$
$$ \begin{align*}\Lambda (L_{\bullet}) \xrightarrow{g} \Lambda (C_{\bullet}) \xrightarrow{h} \mathbb C;\end{align*} $$
![]() $det(C_{\bullet },L_{\bullet })$
is well-defined as an element of
$det(C_{\bullet },L_{\bullet })$
is well-defined as an element of
2.3.1 Integral structures
Definition 5. (i) An integral structure on a complex vector space V is a pair
![]() $(M,m)$
consisting of a lattice
$(M,m)$
consisting of a lattice
![]() $M\subset V$
and a positive rational number
$M\subset V$
and a positive rational number
![]() $m\in \mathbb Q_{>0}$
.
$m\in \mathbb Q_{>0}$
.
(ii) The Euler characteristic of a map from
![]() $(M,m)$
on V to
$(M,m)$
on V to
![]() $(N,n)$
on W is the determinant of the map
$(N,n)$
on W is the determinant of the map
![]() $f: V \to W$
(with respect to the lattices M and N) multiplied by
$f: V \to W$
(with respect to the lattices M and N) multiplied by
![]() $n/m$
.
$n/m$
.
(iii) Two integral structures
![]() $(M,m)$
and
$(M,m)$
and
![]() $(M^{\prime },m^{\prime })$
on V are Euler-equivalent if the Euler characteristic (relative to M and
$(M^{\prime },m^{\prime })$
on V are Euler-equivalent if the Euler characteristic (relative to M and
![]() $M^{\prime }$
) of the identity map on V is one.
$M^{\prime }$
) of the identity map on V is one.
(iv) The
![]() $\mathbb Z$
-dual of
$\mathbb Z$
-dual of
![]() $(M,m)$
is the integral structure
$(M,m)$
is the integral structure
 $(\textrm {Hom}_{\mathbb Z}(M,\mathbb Z), \frac {1}{m})$
on
$(\textrm {Hom}_{\mathbb Z}(M,\mathbb Z), \frac {1}{m})$
on
![]() $\textrm {Hom}_{\mathbb C}(V, \mathbb C)$
.
$\textrm {Hom}_{\mathbb C}(V, \mathbb C)$
.
The Euler characteristic of f in (ii) does not change if
![]() $(M,m)$
is replaced with a Euler-equivalent integral structure
$(M,m)$
is replaced with a Euler-equivalent integral structure
![]() $(M^{\prime },m^{\prime })$
on V. If
$(M^{\prime },m^{\prime })$
on V. If
![]() $M^{\prime }$
is a sublattice of M with index e, then
$M^{\prime }$
is a sublattice of M with index e, then
![]() $(M^{\prime }, em)$
and
$(M^{\prime }, em)$
and
![]() $(M,m)$
are Euler-equivalent, as are
$(M,m)$
are Euler-equivalent, as are
![]() $(\textrm {Hom}_{\mathbb Z}(M,\mathbb Z), 1)$
and
$(\textrm {Hom}_{\mathbb Z}(M,\mathbb Z), 1)$
and
![]() $(\textrm {Hom}_{\mathbb Z}(M^{\prime },\mathbb Z), 1/e)$
: Euler equivalence is compatible with duality.
$(\textrm {Hom}_{\mathbb Z}(M^{\prime },\mathbb Z), 1/e)$
: Euler equivalence is compatible with duality.
If
![]() $\phi :A \to V$
is a homomorphism, A is a finitely generated abelian group,
$\phi :A \to V$
is a homomorphism, A is a finitely generated abelian group,
![]() $\textrm {Ker}(\phi )$
is finite and
$\textrm {Ker}(\phi )$
is finite and
![]() $\phi (A)$
is a lattice in V, then
$\phi (A)$
is a lattice in V, then
![]() $(\phi (A), [\textrm {Ker}(\phi )])$
is an integral structure. If A is torsion-free,
$(\phi (A), [\textrm {Ker}(\phi )])$
is an integral structure. If A is torsion-free,
![]() $(\phi (A), 1)$
essentially determines
$(\phi (A), 1)$
essentially determines
![]() $\phi $
.
$\phi $
.
2.3.2 Integral structures on complexes
Given a finite complex
![]() $C_{\bullet }$
of finite-dimensional complex vector spaces, an integral structure L on
$C_{\bullet }$
of finite-dimensional complex vector spaces, an integral structure L on
![]() $C_{\bullet }$
is a collection
$C_{\bullet }$
is a collection
![]() $L_{\bullet } = (L_{i}, t_{i})$
where
$L_{\bullet } = (L_{i}, t_{i})$
where
![]() $L_{i}$
is a lattice in
$L_{i}$
is a lattice in
![]() $C_{i}$
and
$C_{i}$
and
![]() $t_{i}$
is a positive rational number. If
$t_{i}$
is a positive rational number. If
![]() $C_{\bullet }$
is exact, we define
$C_{\bullet }$
is exact, we define
 $$ \begin{align*}\chi (C_{\bullet}, L_{\bullet}) = \frac{det (C_{\bullet}, L_{\bullet} )}{T} \in {\mathbb C^{\times}}/{\{\pm 1\}}, \qquad T = \frac{t_{0}\cdot ~\cdot~t_{2}~.\cdots}{t_{1}~\cdot~t_{3}~\cdot~\cdots} \in \mathbb Q_{>0}.\end{align*} $$
$$ \begin{align*}\chi (C_{\bullet}, L_{\bullet}) = \frac{det (C_{\bullet}, L_{\bullet} )}{T} \in {\mathbb C^{\times}}/{\{\pm 1\}}, \qquad T = \frac{t_{0}\cdot ~\cdot~t_{2}~.\cdots}{t_{1}~\cdot~t_{3}~\cdot~\cdots} \in \mathbb Q_{>0}.\end{align*} $$
Here, T is a multiplicative Euler characteristic.
Example 6. A collection
![]() $\phi $
of homomorphisms
$\phi $
of homomorphisms
![]() $\phi _{i}: A_{i} \to C_{i}$
where, for all i,
$\phi _{i}: A_{i} \to C_{i}$
where, for all i,
![]() $A_{i}$
is a finitely generated abelian group,
$A_{i}$
is a finitely generated abelian group,
![]() $\textrm {Ker}(\phi _{i})$
is finite and
$\textrm {Ker}(\phi _{i})$
is finite and
![]() $\textrm {Im}(\phi _{i})$
is a lattice in
$\textrm {Im}(\phi _{i})$
is a lattice in
![]() $C_{i}$
gives an integral structure
$C_{i}$
gives an integral structure
![]() $L_{\bullet }= (L_{i}, t_{i}) $
where
$L_{\bullet }= (L_{i}, t_{i}) $
where
![]() $L_{i}= \phi _{i}(A_{i})$
and
$L_{i}= \phi _{i}(A_{i})$
and
![]() $t_{i} =[\textrm {Ker}(\phi _{i})]$
; in this case, we write
$t_{i} =[\textrm {Ker}(\phi _{i})]$
; in this case, we write
![]() $T= \chi (A_{tor})$
. If
$T= \chi (A_{tor})$
. If
![]() $C_{\bullet }$
is exact, then we have
$C_{\bullet }$
is exact, then we have
 $$ \begin{align*}\chi (C_{\bullet}, A_{\bullet}) = \frac{det (C_{\bullet}, L_{\bullet} )}{ \chi (A_{tor})} \in {\mathbb C^{\times}}/{\{\pm 1\}}.\end{align*} $$
$$ \begin{align*}\chi (C_{\bullet}, A_{\bullet}) = \frac{det (C_{\bullet}, L_{\bullet} )}{ \chi (A_{tor})} \in {\mathbb C^{\times}}/{\{\pm 1\}}.\end{align*} $$
We often refer to
![]() $A_{\bullet }$
as an integral structure on
$A_{\bullet }$
as an integral structure on
![]() $C_{\bullet }$
.
$C_{\bullet }$
.
If there is a canonical integral structure
![]() $L_{\bullet }$
on
$L_{\bullet }$
on
![]() $C_{\bullet }$
, then we write
$C_{\bullet }$
, then we write
![]() $det(C_{\bullet })$
and
$det(C_{\bullet })$
and
![]() $\chi (C_{\bullet })$
for
$\chi (C_{\bullet })$
for
![]() $det(C_{\bullet },L_{\bullet })$
and
$det(C_{\bullet },L_{\bullet })$
and
![]() $\chi (C_{\bullet },L_{\bullet })$
.
$\chi (C_{\bullet },L_{\bullet })$
.
2.3.3 Integral structures on
 $\mathcal O_{F}$
-modules
$\mathcal O_{F}$
-modules
Let M be a finitely generated
![]() $\mathcal O_{F}$
-module of rank d; there are two natural integral structures
$\mathcal O_{F}$
-module of rank d; there are two natural integral structures
![]() $i_{M}$
and
$i_{M}$
and
![]() $j_{M}$
on
$j_{M}$
on
![]() $V= M\otimes _{\mathbb Z}\mathbb C $
. Let
$V= M\otimes _{\mathbb Z}\mathbb C $
. Let
![]() $\phi : M \to V$
be the canonical map. The integral structure
$\phi : M \to V$
be the canonical map. The integral structure
![]() $i_{M}$
is obtained by entirely forgetting the
$i_{M}$
is obtained by entirely forgetting the
![]() $\mathcal O_{F}$
-structure:
$\mathcal O_{F}$
-structure:
While
![]() $i_{M}$
appears in the conjectural formula (1), anotherFootnote
1
integral structure
$i_{M}$
appears in the conjectural formula (1), anotherFootnote
1
integral structure
![]() $j_{M}$
appears in Conjecture 20;
$j_{M}$
appears in Conjecture 20;
![]() $j_{M}$
uses the
$j_{M}$
uses the
![]() $\mathcal O_{F}$
-structure on M. Recall the standard isomorphism
$\mathcal O_{F}$
-structure on M. Recall the standard isomorphism
that sends
![]() $x\otimes 1\in \mathcal O_{F}\otimes \mathbb C$
to the element of
$x\otimes 1\in \mathcal O_{F}\otimes \mathbb C$
to the element of
![]() $\mathbb C^{r_{1}+2r_{2}}$
given by the collection of
$\mathbb C^{r_{1}+2r_{2}}$
given by the collection of
![]() $\sigma (x)$
as
$\sigma (x)$
as
![]() $\sigma \in \tilde {S}$
runs through the embeddings of F in
$\sigma \in \tilde {S}$
runs through the embeddings of F in
![]() $\mathbb C$
. Define
$\mathbb C$
. Define
![]() $M_{\sigma } = M\otimes _{\mathcal O_{F}} \mathbb C$
using
$M_{\sigma } = M\otimes _{\mathcal O_{F}} \mathbb C$
using
![]() $\sigma : F\to \mathbb C$
.
$\sigma : F\to \mathbb C$
.
The isomorphism (6) shows
 $$ \begin{align*}V= M\otimes_{\mathbb Z}\mathbb C \cong M \otimes_{\mathcal O_{F}} (\mathcal O_{F}\otimes_{\mathbb Z} \mathbb C) \cong M\otimes_{\mathcal O_{F}}\mathbb C^{r_{1}+2r_{2}} \cong \prod_{\sigma \in \tilde{S}} M_{\sigma}.\end{align*} $$
$$ \begin{align*}V= M\otimes_{\mathbb Z}\mathbb C \cong M \otimes_{\mathcal O_{F}} (\mathcal O_{F}\otimes_{\mathbb Z} \mathbb C) \cong M\otimes_{\mathcal O_{F}}\mathbb C^{r_{1}+2r_{2}} \cong \prod_{\sigma \in \tilde{S}} M_{\sigma}.\end{align*} $$
Suppose
![]() $B=\{x_{1}, \cdots , x_{d}\} \subset M$
is linearly independent over
$B=\{x_{1}, \cdots , x_{d}\} \subset M$
is linearly independent over
![]() $\mathcal O_{F}$
. Let
$\mathcal O_{F}$
. Let
![]() $\{\epsilon _{j}\}$
be the standard basis of
$\{\epsilon _{j}\}$
be the standard basis of
![]() $ \mathbb C^{r_{1}+2r_{2}}$
. Define
$ \mathbb C^{r_{1}+2r_{2}}$
. Define
 $\tilde {B} = <x_{i}\otimes \epsilon _{j}>$
to be the
$\tilde {B} = <x_{i}\otimes \epsilon _{j}>$
to be the
![]() $\mathbb Z$
-span of
$\mathbb Z$
-span of
![]() $x_{i}\otimes \epsilon _{j}$
inside V. Consider the integral structure
$x_{i}\otimes \epsilon _{j}$
inside V. Consider the integral structure
![]() $i(B)= (\tilde {B}, b)$
where b is the order of the quotient of M by the
$i(B)= (\tilde {B}, b)$
where b is the order of the quotient of M by the
![]() $\mathcal O_{F}$
-submodule
$\mathcal O_{F}$
-submodule
![]() $<x_{1}, \cdots , x_{d}>$
generated by B.
$<x_{1}, \cdots , x_{d}>$
generated by B.
Proposition 7. For any two such subsets B and
![]() $B^{\prime }$
of M,
$B^{\prime }$
of M,
![]() $i(B)$
and
$i(B)$
and
![]() $i(B^{\prime })$
are Euler-equivalent.
$i(B^{\prime })$
are Euler-equivalent.
Proof. Let
![]() $B^{\prime } =\{c_{1}x_{1}, c_{2}x_{2}, \cdots , c_{d}x_{d}\}$
and
$B^{\prime } =\{c_{1}x_{1}, c_{2}x_{2}, \cdots , c_{d}x_{d}\}$
and
![]() $C = c_{1}.c_{2}\cdots c_{d}$
and consider
$C = c_{1}.c_{2}\cdots c_{d}$
and consider
![]() $i(B^{\prime })$
. As b and
$i(B^{\prime })$
. As b and
![]() $b^{\prime }$
are related by
$b^{\prime }$
are related by
![]() $b^{\prime } = C.b$
and the determinant of the identity map of V with respect to
$b^{\prime } = C.b$
and the determinant of the identity map of V with respect to
![]() $i(B)$
and
$i(B)$
and
![]() $i(B^{\prime })$
is C,
$i(B^{\prime })$
is C,
![]() $i(B)$
and
$i(B)$
and
![]() $i(B^{\prime })$
are Euler-equivalent. Given B and
$i(B^{\prime })$
are Euler-equivalent. Given B and
![]() $B^{\prime }$
, one can find
$B^{\prime }$
, one can find
![]() $B^{\prime \prime }$
such that the previous argument applies to the pairs
$B^{\prime \prime }$
such that the previous argument applies to the pairs
![]() $B, B^{\prime \prime }$
and
$B, B^{\prime \prime }$
and
![]() $B^{\prime }, B^{\prime \prime }$
.
$B^{\prime }, B^{\prime \prime }$
.
Definition 8. For any finitely generated
![]() $\mathcal O_{F}$
-module M, the
$\mathcal O_{F}$
-module M, the
![]() $\mathcal O_{F}$
-integral structure
$\mathcal O_{F}$
-integral structure
![]() $j_{M}$
on
$j_{M}$
on
![]() $V =M\otimes _{\mathbb Z}\mathbb C$
is the Euler equivalence class in Proposition 7.
$V =M\otimes _{\mathbb Z}\mathbb C$
is the Euler equivalence class in Proposition 7.
2.3.4 Results on integral structures
Let M be a finitely generated
![]() $\mathcal O_{F}$
-module of rank d.
$\mathcal O_{F}$
-module of rank d.
Proposition 9. (i) The Euler characteristic of the identity map on V from
![]() $i_{M}$
to
$i_{M}$
to
![]() $j_{M}$
is
$j_{M}$
is
![]() $(\sqrt {d_{F}})^{d}$
.
$(\sqrt {d_{F}})^{d}$
.
(ii) Let M be torsion-free and
![]() $M^{\vee }= \textrm {Hom}_{\mathcal O_{F}}(M, \mathcal O_{F})$
. The
$M^{\vee }= \textrm {Hom}_{\mathcal O_{F}}(M, \mathcal O_{F})$
. The
![]() $\mathbb Z$
-dual of
$\mathbb Z$
-dual of
![]() $j_{M}$
is the
$j_{M}$
is the
![]() $\mathcal O_{F}$
-integral structure
$\mathcal O_{F}$
-integral structure
![]() $j_{M^{\vee }}$
.
$j_{M^{\vee }}$
.
Proof. (i) Write
![]() $\kappa _{M}$
for the Euler characteristic. For
$\kappa _{M}$
for the Euler characteristic. For
![]() $M =\mathcal O_{F}$
, this says
$M =\mathcal O_{F}$
, this says
![]() $\sqrt {d_{F}}$
is the determinant of the standard map
$\sqrt {d_{F}}$
is the determinant of the standard map
![]() $\psi : \mathcal O_{F}\otimes _{\mathbb Z} \mathbb C \to \mathbb Z^{r_{1}+2r_{2}}\otimes \mathbb C$
in (6). So
$\psi : \mathcal O_{F}\otimes _{\mathbb Z} \mathbb C \to \mathbb Z^{r_{1}+2r_{2}}\otimes \mathbb C$
in (6). So
 $\kappa _{M}= \sqrt {d_{F}}^{d}$
if M is free of finite rank
$\kappa _{M}= \sqrt {d_{F}}^{d}$
if M is free of finite rank
![]() $d>0$
. Even if M is not free, it contains a free submodule
$d>0$
. Even if M is not free, it contains a free submodule
![]() $M^{\prime }$
of finite index. As
$M^{\prime }$
of finite index. As
![]() $\kappa _{M} = \kappa _{M^{\prime }}$
, the claim for
$\kappa _{M} = \kappa _{M^{\prime }}$
, the claim for
![]() $M^{\prime }$
implies the one for M.
$M^{\prime }$
implies the one for M.
(ii) Define the index
![]() $(M:N)$
of any two torsion-free
$(M:N)$
of any two torsion-free
![]() $\mathcal O_{F}$
-modules M and N of rank d inside V by
$\mathcal O_{F}$
-modules M and N of rank d inside V by
![]() $(M:N) = (M:P)/(N:P)$
for any submodule P of finite index contained in M and N. Let
$(M:N) = (M:P)/(N:P)$
for any submodule P of finite index contained in M and N. Let
![]() $\{x_{1}, \cdots , x_{d}\}$
be a basis of
$\{x_{1}, \cdots , x_{d}\}$
be a basis of
![]() $V= M\otimes _{\mathcal O_{F}}F$
. Let
$V= M\otimes _{\mathcal O_{F}}F$
. Let
![]() $\{\epsilon _{j}\}$
be the standard basis of
$\{\epsilon _{j}\}$
be the standard basis of
![]() $ \mathbb C^{r_{1}+2r_{2}}$
. Let
$ \mathbb C^{r_{1}+2r_{2}}$
. Let
![]() $\{y_{1}, \cdots , y_{d}\}$
be an F-basis of
$\{y_{1}, \cdots , y_{d}\}$
be an F-basis of
![]() $M^{\vee }\otimes _{\mathcal O_{F}}F$
dual to
$M^{\vee }\otimes _{\mathcal O_{F}}F$
dual to
![]() $\{x_{1}, \cdots , x_{d}\}$
. Then
$\{x_{1}, \cdots , x_{d}\}$
. Then
![]() $(<x_{i}\otimes \epsilon _{j}>, (M: <x_{1}, \cdots , x_{d}>))$
is a representative for the
$(<x_{i}\otimes \epsilon _{j}>, (M: <x_{1}, \cdots , x_{d}>))$
is a representative for the
![]() $\mathcal O_{F}$
-integral structure
$\mathcal O_{F}$
-integral structure
![]() $j_{M}$
. Its
$j_{M}$
. Its
![]() $\mathbb Z$
-dual is
$\mathbb Z$
-dual is
![]() $(<y\otimes \epsilon _{j}>, (<x_{1}, \cdots , x_{d}>: M))$
. But
$(<y\otimes \epsilon _{j}>, (<x_{1}, \cdots , x_{d}>: M))$
. But
![]() $(<y\otimes \epsilon _{j}>, (M^{\vee }: <y\otimes \epsilon _{j}>))$
is a representative for
$(<y\otimes \epsilon _{j}>, (M^{\vee }: <y\otimes \epsilon _{j}>))$
is a representative for
![]() $j_{M^{\vee }}$
, and since
$j_{M^{\vee }}$
, and since
![]() $(M:N)^{-1} = (M^{\vee }, N^{\vee })$
, we are done.
$(M:N)^{-1} = (M^{\vee }, N^{\vee })$
, we are done.
2.3.5 Pairings and determinants
Let N be a finitely generated abelian group and
![]() $\psi : N/{N_{tor}} \times N/{N_{tor}} \to \mathbb R$
be a nondegenerate symmetric bilinear form on N. One defines
$\psi : N/{N_{tor}} \times N/{N_{tor}} \to \mathbb R$
be a nondegenerate symmetric bilinear form on N. One defines
![]() $\Delta (N) \in \mathbb C^{\times }/{\{\pm 1\}}$
as the determinant of the matrix
$\Delta (N) \in \mathbb C^{\times }/{\{\pm 1\}}$
as the determinant of the matrix
![]() $\psi (b_{i}, b_{j})$
divided by
$\psi (b_{i}, b_{j})$
divided by
![]() $(N: N_{0})^{2}$
where
$(N: N_{0})^{2}$
where
![]() $N_{0}$
is the subgroup of finite index generated by a maximal linearly independent subset
$N_{0}$
is the subgroup of finite index generated by a maximal linearly independent subset
![]() $b_{i}$
of N; therefore,
$b_{i}$
of N; therefore,
![]() $\Delta (N)$
is independent of the choice of
$\Delta (N)$
is independent of the choice of
![]() $b_{i}$
s and incorporates the order of the torsion subgroup of N. We can rewrite
$b_{i}$
s and incorporates the order of the torsion subgroup of N. We can rewrite
![]() $\psi $
as the integral structure
$\psi $
as the integral structure
![]() $(C_{\bullet }, L_{\bullet })$
with
$(C_{\bullet }, L_{\bullet })$
with
![]() $L_{0}=N, L_{1}= \textrm {Hom}(N, \mathbb Z)$
:
$L_{0}=N, L_{1}= \textrm {Hom}(N, \mathbb Z)$
:
 $$ \begin{align*}C_{0}= N\otimes\mathbb C \xrightarrow{\psi_{*}} \textrm{Hom}(N, \mathbb Z)\otimes\mathbb C= C_{1}, \qquad \Delta(N) = \frac{det(\psi_{*}) }{[N_{tor}]^{2}}; \end{align*} $$
$$ \begin{align*}C_{0}= N\otimes\mathbb C \xrightarrow{\psi_{*}} \textrm{Hom}(N, \mathbb Z)\otimes\mathbb C= C_{1}, \qquad \Delta(N) = \frac{det(\psi_{*}) }{[N_{tor}]^{2}}; \end{align*} $$
here
![]() $det(C_{\bullet }, L_{\bullet })$
is the determinant
$det(C_{\bullet }, L_{\bullet })$
is the determinant
![]() $\det (\psi _{*})$
of
$\det (\psi _{*})$
of
![]() $\psi $
computed with the bases
$\psi $
computed with the bases
![]() $L_{0}$
and
$L_{0}$
and
![]() $L_{1}$
. Given a short exact sequence of finitely generated groups
$L_{1}$
. Given a short exact sequence of finitely generated groups
![]() $ 0 \to N^{\prime } \to N \to N^{\prime \prime } \to 0$
which splits over
$ 0 \to N^{\prime } \to N \to N^{\prime \prime } \to 0$
which splits over
![]() $\mathbb Q$
as an orthogonal direct sum
$\mathbb Q$
as an orthogonal direct sum
 $$ \begin{align*}N_{\mathbb Q} \cong N^{\prime}_{\mathbb Q} \oplus N^{\prime\prime}_{\mathbb Q}\end{align*} $$
$$ \begin{align*}N_{\mathbb Q} \cong N^{\prime}_{\mathbb Q} \oplus N^{\prime\prime}_{\mathbb Q}\end{align*} $$
with respect to a definite pairing
![]() $\psi $
on N, one has the following standard relation:
$\psi $
on N, one has the following standard relation:
2.4 Motives
We start with the integral structures underlying the Betti and de Rham realisations of the motives
![]() $M= h^{j}(V_{0})(r)$
for
$M= h^{j}(V_{0})(r)$
for
![]() $0\le j \le 2(d-1)$
.
$0\le j \le 2(d-1)$
.
Definition 10. The integral structure
 $H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))^{+}$
is defined as the complex vector space
$H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))^{+}$
is defined as the complex vector space
 $H^{j}_{B}(V_{\mathbb C}, \mathbb C(r))^{+}$
together with the homomorphism
$H^{j}_{B}(V_{\mathbb C}, \mathbb C(r))^{+}$
together with the homomorphism
 $$ \begin{align*}H^{j}_{B}(V_{\mathbb C}, \mathbb Z)^{+} \to H^{j}_{B}(V_{\mathbb C}, \mathbb C)^{+}\xrightarrow{\times (2\pi i)^{r}} H^{j}_{B}(V_{\mathbb C}, \mathbb C(r))^{+} ;\end{align*} $$
$$ \begin{align*}H^{j}_{B}(V_{\mathbb C}, \mathbb Z)^{+} \to H^{j}_{B}(V_{\mathbb C}, \mathbb C)^{+}\xrightarrow{\times (2\pi i)^{r}} H^{j}_{B}(V_{\mathbb C}, \mathbb C(r))^{+} ;\end{align*} $$
the first map is the natural map and the second map is multiplication by
![]() $(2\pi i)^{r}$
.
$(2\pi i)^{r}$
.
Example 11. When
![]() $V=S$
, one has
$V=S$
, one has
![]() $H^{0}(S_{\mathbb C}, \mathbb Z(r))^{+}$
is isomorphic to
$H^{0}(S_{\mathbb C}, \mathbb Z(r))^{+}$
is isomorphic to
![]() $\mathbb Z^{r_{2}}$
when r is odd and
$\mathbb Z^{r_{2}}$
when r is odd and
![]() $\mathbb Z^{r_{1}+r_{2}}$
when r is even.
$\mathbb Z^{r_{1}+r_{2}}$
when r is even.
2.5 de Rham realisation of
 $M= h^{j}(V_{0})(r)$
$M= h^{j}(V_{0})(r)$
The de Rham realisation
 $M_{dR} = H^{j}_{dR}(V_{\mathbb C}, \mathbb C(r))$
is
$M_{dR} = H^{j}_{dR}(V_{\mathbb C}, \mathbb C(r))$
is
 $H^{j}_{dR}(V_{\mathbb C}, \mathbb C)$
with the Hodge filtration shifted by r; that is, the Tate twist in de Rham realisation shifts the Hodge filtration but does not change the vector space. The tangent space
$H^{j}_{dR}(V_{\mathbb C}, \mathbb C)$
with the Hodge filtration shifted by r; that is, the Tate twist in de Rham realisation shifts the Hodge filtration but does not change the vector space. The tangent space
![]() $(t_{M})_{\mathbb C}$
of M is defined as follows:
$(t_{M})_{\mathbb C}$
of M is defined as follows:
 $$ \begin{align*}(t_{M})_{\mathbb C} = \frac{H^{j}_{dR}(V_{\mathbb C}, \mathbb C(r))}{F^{0}} = \prod_{k<r} H^{j-k}(V_{\mathbb C}, \Omega^{k}_{V_{\mathbb C}}) = \prod_{\sigma \in \tilde{S} }~ \prod_{k<r} H^{j-k}(V_{\sigma}, \Omega^{k}_{V_{\sigma}}).\end{align*} $$
$$ \begin{align*}(t_{M})_{\mathbb C} = \frac{H^{j}_{dR}(V_{\mathbb C}, \mathbb C(r))}{F^{0}} = \prod_{k<r} H^{j-k}(V_{\mathbb C}, \Omega^{k}_{V_{\mathbb C}}) = \prod_{\sigma \in \tilde{S} }~ \prod_{k<r} H^{j-k}(V_{\sigma}, \Omega^{k}_{V_{\sigma}}).\end{align*} $$
Let
 $\lambda ^{k}\Omega _{V/S}$
denote the kth derived exterior power of the sheaf
$\lambda ^{k}\Omega _{V/S}$
denote the kth derived exterior power of the sheaf
![]() $\Omega _{V/S}$
on V; see the appendix of [Reference Lichtenbaum27].
$\Omega _{V/S}$
on V; see the appendix of [Reference Lichtenbaum27].
Definition 12. The integral structure on the complex vector space
![]() $(t_{M})_{\mathbb C}$
is given by the map
$(t_{M})_{\mathbb C}$
is given by the map
 $$ \begin{align*}t_{M}:= \prod_{k<r} H^{j-k}(V, \lambda^{k} \Omega_{V/S}) \to \prod_{\sigma \in \tilde{S}}~ \prod_{k<r} H^{j-k}(V_{\sigma}, \Omega^{k}_{V_{\sigma}}) = (t_{M})_{\mathbb C}.\end{align*} $$
$$ \begin{align*}t_{M}:= \prod_{k<r} H^{j-k}(V, \lambda^{k} \Omega_{V/S}) \to \prod_{\sigma \in \tilde{S}}~ \prod_{k<r} H^{j-k}(V_{\sigma}, \Omega^{k}_{V_{\sigma}}) = (t_{M})_{\mathbb C}.\end{align*} $$
As in (5), one views
 $H^{j-k}(V, \lambda ^{k} \Omega _{V/S}) $
as an abelian group; its structure as a module over
$H^{j-k}(V, \lambda ^{k} \Omega _{V/S}) $
as an abelian group; its structure as a module over
![]() $\mathcal O_{F}$
is not used.
$\mathcal O_{F}$
is not used.
Remark 13. We can use the Hodge decomposition of
![]() $(t_{M})_{\mathbb C}$
to decompose the period map
$(t_{M})_{\mathbb C}$
to decompose the period map
![]() $\alpha _{M}$
of (3) as a sum of
$\alpha _{M}$
of (3) as a sum of
![]() $\alpha _{k}$
where
$\alpha _{k}$
where
![]() $\alpha _{k}$
is the composite map
$\alpha _{k}$
is the composite map
 $$ \begin{align*}H^{j}(V_{\mathbb C}, \mathbb C(r))^{+} \xrightarrow{\alpha} (t_{M})_{\mathbb C} = \prod_{k<r} H^{j-k}(V_{\mathbb C}, \Omega^{k}_{V_{\mathbb C}}) \to H^{j-k}(V_{\mathbb C}, \Omega^{k}_{V_{\mathbb C}}).\end{align*} $$
$$ \begin{align*}H^{j}(V_{\mathbb C}, \mathbb C(r))^{+} \xrightarrow{\alpha} (t_{M})_{\mathbb C} = \prod_{k<r} H^{j-k}(V_{\mathbb C}, \Omega^{k}_{V_{\mathbb C}}) \to H^{j-k}(V_{\mathbb C}, \Omega^{k}_{V_{\mathbb C}}).\end{align*} $$
The enhanced period map
![]() $\gamma _{M}$
of [Reference Lichtenbaum27, §2.3],
$\gamma _{M}$
of [Reference Lichtenbaum27, §2.3],
likewise decomposes as a sum of
![]() $\gamma _{k}:= \Gamma ^{*}(r-k)~\cdot ~\alpha _{k}$
. Here
$\gamma _{k}:= \Gamma ^{*}(r-k)~\cdot ~\alpha _{k}$
. Here
![]() $\Gamma $
is the classical gamma function and
$\Gamma $
is the classical gamma function and
![]() $\Gamma ^{*}(m)$
denotes the special value at
$\Gamma ^{*}(m)$
denotes the special value at
![]() $s=m$
.
$s=m$
.
2.6 Integral structures on certain motivic exact sequences
The conjectural formula (1) from [Reference Lichtenbaum27, Conjecture 3.1] predicts that the special value
![]() $\zeta ^{*}(V,r)$
of
$\zeta ^{*}(V,r)$
of
![]() $\zeta (V,s)$
at
$\zeta (V,s)$
at
![]() $s=r$
is equal to
$s=r$
is equal to
![]() $ \pm \chi (V,r)$
(up to powers of 2) defined as follows:
$ \pm \chi (V,r)$
(up to powers of 2) defined as follows:
 $$ \begin{align*} \chi(V,r)= \frac{\chi_{A,C}(V,r)}{\chi_{B}(V,r)} = \frac{\chi(C(r))~\cdot~\chi_{A}(V,r)~\cdot~\chi_{A^{\prime}}(V,r)}{\chi_{B}(V,r)}.\end{align*} $$
$$ \begin{align*} \chi(V,r)= \frac{\chi_{A,C}(V,r)}{\chi_{B}(V,r)} = \frac{\chi(C(r))~\cdot~\chi_{A}(V,r)~\cdot~\chi_{A^{\prime}}(V,r)}{\chi_{B}(V,r)}.\end{align*} $$
In more detail,
-
•
 $M_{j}$
is the motive
$M_{j}$
is the motive
 $h^{j}(V_{0}, \mathbb Z(r))$
with
$h^{j}(V_{0}, \mathbb Z(r))$
with
 $0\le j \le 2d-2$
with the enhanced period map
$0\le j \le 2d-2$
with the enhanced period map  $$ \begin{align*}\gamma_{M_{j}} : H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))^{+}_{\mathbb C} \to t_{M_{j}}.\end{align*} $$
$$ \begin{align*}\gamma_{M_{j}} : H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))^{+}_{\mathbb C} \to t_{M_{j}}.\end{align*} $$
-
• We fix an integral structure on
 $ \textrm {Ker}(\gamma _{M_{j}})$
and
$ \textrm {Ker}(\gamma _{M_{j}})$
and
 $ \textrm {Coker}(\gamma _{M_{j}})$
for all j and use them implicitly in all that follows. Under this condition, the final conjecture is actually independent of the choice of these integral structures.
$ \textrm {Coker}(\gamma _{M_{j}})$
for all j and use them implicitly in all that follows. Under this condition, the final conjecture is actually independent of the choice of these integral structures. -
• The exact sequences
 $B(j,r)$
with integral structures (8)We write
$B(j,r)$
with integral structures (8)We write $$ \begin{align} 0 \to \textrm{Ker}(\gamma_{M_{j}}) \to H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))^{+}_{\mathbb C} \to t_{M_{j}} \to \textrm{Coker}(\gamma_{M_{j}}) \to 0. \end{align} $$
$$ \begin{align} 0 \to \textrm{Ker}(\gamma_{M_{j}}) \to H^{j}_{B}(V_{\mathbb C}, \mathbb Z(r))^{+}_{\mathbb C} \to t_{M_{j}} \to \textrm{Coker}(\gamma_{M_{j}}) \to 0. \end{align} $$
 $$ \begin{align*}\chi_{B}(V,r) =\prod_{j} (\chi(B(j,r)))^{(-1)^{j}} = \frac{\chi(B(0,r))~\cdot~\chi(B(2,r))~\cdots}{\chi(B(1,r))~\cdot~\chi(B(3,r)) \cdots}.\end{align*} $$
$$ \begin{align*}\chi_{B}(V,r) =\prod_{j} (\chi(B(j,r)))^{(-1)^{j}} = \frac{\chi(B(0,r))~\cdot~\chi(B(2,r))~\cdots}{\chi(B(1,r))~\cdot~\chi(B(3,r)) \cdots}.\end{align*} $$
-
• The integral structures
 $A(j,r)$
for
$A(j,r)$
for
 $0\le j\le \textrm {min}(2d-1, 2r-3)$
and
$0\le j\le \textrm {min}(2d-1, 2r-3)$
and
 $A^{\prime }(j,r)$
for
$A^{\prime }(j,r)$
for
 $2d+1\ge j\ge \textrm {max}(0, 2r+1)$
are defined as (9)We write
$2d+1\ge j\ge \textrm {max}(0, 2r+1)$
are defined as (9)We write $$ \begin{align} A(j,r): H^{j+1}_{W}(V, \mathbb Z(r))_{\mathbb C} \to \textrm{Coker}(\gamma_{M_{j}}), \qquad A^{\prime}(j,r): \textrm{Ker}(\gamma_{M_{j}}) \to H^{j+2}_{W}(V,\mathbb Z(r))_{\mathbb C}. \end{align} $$
(10)The map in
$$ \begin{align} A(j,r): H^{j+1}_{W}(V, \mathbb Z(r))_{\mathbb C} \to \textrm{Coker}(\gamma_{M_{j}}), \qquad A^{\prime}(j,r): \textrm{Ker}(\gamma_{M_{j}}) \to H^{j+2}_{W}(V,\mathbb Z(r))_{\mathbb C}. \end{align} $$
(10)The map in $$ \begin{align} \chi_{A}(V,r) &= \prod_{j=0}^{\textrm{min}(2d-1, 2r-3)} (\chi(A(j,r)))^{(-1)^{j}}, \nonumber\\ \chi_{A^{\prime}}(V,r) &= \prod_{j=\textrm{max}(0, 2r+1) }^{j=2d-1} (\chi(A^{\prime}(j,r)))^{(-1)^{j}}. \end{align} $$
$$ \begin{align} \chi_{A}(V,r) &= \prod_{j=0}^{\textrm{min}(2d-1, 2r-3)} (\chi(A(j,r)))^{(-1)^{j}}, \nonumber\\ \chi_{A^{\prime}}(V,r) &= \prod_{j=\textrm{max}(0, 2r+1) }^{j=2d-1} (\chi(A^{\prime}(j,r)))^{(-1)^{j}}. \end{align} $$
 $A(j,r)$
is Beilinson’s regulator from (4), usually stated as a map from algebraic K-theory of
$A(j,r)$
is Beilinson’s regulator from (4), usually stated as a map from algebraic K-theory of
 $V_{0}$
to the Deligne cohomology of
$V_{0}$
to the Deligne cohomology of
 $V_{0}$
; it is conjectured to be an isomorphism. The group
$V_{0}$
; it is conjectured to be an isomorphism. The group
 $\textrm {Ker}(M_{2d-2-j, d-r})$
can be identified with the dual of
$\textrm {Ker}(M_{2d-2-j, d-r})$
can be identified with the dual of
 $\textrm {Coker}(M_{j,r})$
- see [Reference Lichtenbaum27, §2] or [Reference Fontaine15, §6.9]. The integral structures
$\textrm {Coker}(M_{j,r})$
- see [Reference Lichtenbaum27, §2] or [Reference Fontaine15, §6.9]. The integral structures
 $A^{\prime }(j,r)$
are defined as the dual of
$A^{\prime }(j,r)$
are defined as the dual of
 $A(2d-2-j,d-r)$
in [Reference Lichtenbaum27].
$A(2d-2-j,d-r)$
in [Reference Lichtenbaum27].
-
• The exact sequence
 $C(r)_{\mathbb C}$
with integral structure (for
$C(r)_{\mathbb C}$
with integral structure (for
 $0 \le r\le d$
) (11)The maps here are integral versions of the maps from (4): the first is Beilinson’s regulator, the second is the dual of the cycle map, the third is the Arakelov intersection/height pairing map, the fourth map is the cycle class map and the fifth is the dual of Beilinson’s regulator. Beilinson’s conjectures [Reference Lichtenbaum27, Conjectures 2.3.4-2.3.7] imply that
$0 \le r\le d$
) (11)The maps here are integral versions of the maps from (4): the first is Beilinson’s regulator, the second is the dual of the cycle map, the third is the Arakelov intersection/height pairing map, the fourth map is the cycle class map and the fifth is the dual of Beilinson’s regulator. Beilinson’s conjectures [Reference Lichtenbaum27, Conjectures 2.3.4-2.3.7] imply that $$ \begin{align} 0 &\to H^{2r-1}_{W}(V, \mathbb Z(r))_{\mathbb C} \to \textrm{Coker}(\gamma_{M_{2r-2}}) \to H^{2r+1}_{W}(V, \mathbb Z(r))_{\mathbb C} \xrightarrow{h}\nonumber\\[3pt] &\to H^{2r}_{W}(V, \mathbb Z(r))_{\mathbb C} \to \textrm{Ker}(\gamma_{M_{2r}}) \to H^{2r+2}_{W}(V, \mathbb Z(r))_{\mathbb C} \to 0.\end{align} $$
$$ \begin{align} 0 &\to H^{2r-1}_{W}(V, \mathbb Z(r))_{\mathbb C} \to \textrm{Coker}(\gamma_{M_{2r-2}}) \to H^{2r+1}_{W}(V, \mathbb Z(r))_{\mathbb C} \xrightarrow{h}\nonumber\\[3pt] &\to H^{2r}_{W}(V, \mathbb Z(r))_{\mathbb C} \to \textrm{Ker}(\gamma_{M_{2r}}) \to H^{2r+2}_{W}(V, \mathbb Z(r))_{\mathbb C} \to 0.\end{align} $$
 $C(r)_{\mathbb C}$
is exact; we refer to [Reference Lichtenbaum27, §2] for more details. Integral versions of (4) have also been introduced by Flach–Morin [Reference Flach and Morin12, Conjecture 2.9 and (28), (29)].
$C(r)_{\mathbb C}$
is exact; we refer to [Reference Lichtenbaum27, §2] for more details. Integral versions of (4) have also been introduced by Flach–Morin [Reference Flach and Morin12, Conjecture 2.9 and (28), (29)].
Remark 14. (see Table 1) (i) By [Reference Fontaine15, §7.1] or [Reference Nekovář34, §2.1 and (2.2.1)], if the weight of M is positive (so
![]() $j>2r$
), then one has
$j>2r$
), then one has
![]() $\textrm {Coker}(\gamma _{M}) =0$
. Dually, if
$\textrm {Coker}(\gamma _{M}) =0$
. Dually, if
![]() $j-2r <0$
, then one has
$j-2r <0$
, then one has
![]() $\textrm {Ker}(\gamma _{M}) =0$
. It remains to consider the case
$\textrm {Ker}(\gamma _{M}) =0$
. It remains to consider the case
![]() $M= h^{2r}(V_{0}, \mathbb Z(r))$
. Since
$M= h^{2r}(V_{0}, \mathbb Z(r))$
. Since
![]() $N = h^{2r}(V_{0}, \mathbb Z(r+1))$
has negative weight, it follows that
$N = h^{2r}(V_{0}, \mathbb Z(r+1))$
has negative weight, it follows that
![]() $\textrm {Ker}( \gamma _{N})=0$
. Hence,
$\textrm {Ker}( \gamma _{N})=0$
. Hence,
![]() $\textrm {Coker}(\gamma _{M_{2r}}) =0$
as it is dual to
$\textrm {Coker}(\gamma _{M_{2r}}) =0$
as it is dual to
![]() $\textrm {Ker}( \gamma _{N})$
.
$\textrm {Ker}( \gamma _{N})$
.
(ii) Note that each group
![]() $H^{i}_{W}(V,\mathbb Z(r))$
appears exactly once.
$H^{i}_{W}(V,\mathbb Z(r))$
appears exactly once.
All of the exact sequences above are variants of motivic exact sequences (4) but equipped with an integral structure. Our convention is that the terms
![]() $ \textrm {Ker}(\gamma _{M})$
have even degree and
$ \textrm {Ker}(\gamma _{M})$
have even degree and
![]() $\textrm {Coker}(\gamma _{M})$
have odd degree. If
$\textrm {Coker}(\gamma _{M})$
have odd degree. If
![]() $j=2r-1$
, then
$j=2r-1$
, then
![]() $\textrm {Ker}(\gamma _{M_{j}})=0 = \textrm {Coker}(\gamma _{M_{j}})$
; if
$\textrm {Ker}(\gamma _{M_{j}})=0 = \textrm {Coker}(\gamma _{M_{j}})$
; if
![]() $j \neq 2r-1$
, these terms occur exactly twice in the conjecture, once in the B-complexes and once in A,
$j \neq 2r-1$
, these terms occur exactly twice in the conjecture, once in the B-complexes and once in A,
![]() $A^{\prime }$
and C-complexes. Since
$A^{\prime }$
and C-complexes. Since
![]() $\chi _{B}$
is the denominator and the others (
$\chi _{B}$
is the denominator and the others (
![]() $\chi _{A}$
,
$\chi _{A}$
,
![]() $\chi _{A^{\prime }}$
and
$\chi _{A^{\prime }}$
and
![]() $\chi (C)$
) are in the numerator of
$\chi (C)$
) are in the numerator of
![]() $\chi (V,r)$
, the conjecture is independent of the choice of integral structures on the terms
$\chi (V,r)$
, the conjecture is independent of the choice of integral structures on the terms
![]() $ \textrm {Ker}(\gamma _{M})$
and
$ \textrm {Ker}(\gamma _{M})$
and
![]() $\textrm {Coker}(\gamma _{M})$
.
$\textrm {Coker}(\gamma _{M})$
.
(iii) The conjectural formula (1) from [Reference Lichtenbaum27, Conjecture 3.1] tacitly assumes the generalised Beilinson–Soulé conjecture from [Reference Lichtenbaum27] which predicts
If this is not assumed, then (10) has to be replaced with
 $$ \begin{align*}\chi_{A}(V,r) = \prod_{j=0}^{2r-3} (\chi(A(j,r)))^{(-1)^{j}}, \qquad \chi_{A^{\prime}}(V,r) = \prod_{j=2r+1}^{j=2d-1} (\chi(A^{\prime}(j,r)))^{(-1)^{j}}\end{align*} $$
$$ \begin{align*}\chi_{A}(V,r) = \prod_{j=0}^{2r-3} (\chi(A(j,r)))^{(-1)^{j}}, \qquad \chi_{A^{\prime}}(V,r) = \prod_{j=2r+1}^{j=2d-1} (\chi(A^{\prime}(j,r)))^{(-1)^{j}}\end{align*} $$
and the limits on j in the first two lines of Table 1 have to be replaced with
![]() $2d+2> j>2r+2$
(in the first line) and
$2d+2> j>2r+2$
(in the first line) and
![]() $0< j< 2r-1$
(in the second line). We refer to [Reference Lichtenbaum27] for more details.
$0< j< 2r-1$
(in the second line). We refer to [Reference Lichtenbaum27] for more details.
Table 1 Tabulation of invariants in the various integral structures for the motives
![]() $M_{j} =h^{j}(V_{0})(r)$
$M_{j} =h^{j}(V_{0})(r)$

(iv) We refer to [Reference Lichtenbaum27] for the conjectures such as the finite generation of
![]() $H^{*}_{W}(V, \mathbb Z(r))$
which are implicit in the formulation of (1).
$H^{*}_{W}(V, \mathbb Z(r))$
which are implicit in the formulation of (1).
It is instructive to consider the conjecture [Reference Lichtenbaum27, Conjecture 3.1] in the case of number fields before delving into the case of arithmetic surfaces.
2.7 The case of number fields:
 $V=S$
,
$V=S$
,
 $d=1$
and
$d=1$
and
 $r=0$
and
$r=0$
and
 $r=1$
$r=1$
This example is worked out in [Reference Lichtenbaum27, §7].
2.7.1 The case
 $r=0$
$r=0$
The motives are
![]() $M_{j} =h^{j}(S)(0)$
.
$M_{j} =h^{j}(S)(0)$
.
We know
 $H^{j}_{et}(S, \mathbb Z(1)) =0$
if
$H^{j}_{et}(S, \mathbb Z(1)) =0$
if
![]() $j <1$
and that
$j <1$
and that
![]() $H^{1}_{et}(S, \mathbb Z(1)) = \mathcal O_{F}^{\times }$
,
$H^{1}_{et}(S, \mathbb Z(1)) = \mathcal O_{F}^{\times }$
,
![]() $H^{2}_{et}(S, \mathbb Z(1)) = \textrm {Pic}(S)$
,
$H^{2}_{et}(S, \mathbb Z(1)) = \textrm {Pic}(S)$
,
![]() $H^{3}_{et}(S, \mathbb Z(1)) =0$
(up to a finite 2-group) and
$H^{3}_{et}(S, \mathbb Z(1)) =0$
(up to a finite 2-group) and
![]() $H^{0}_{et}(S, \mathbb Z(0)) = \mathbb Z$
.
$H^{0}_{et}(S, \mathbb Z(0)) = \mathbb Z$
.
It immediately follows from the definitions that
![]() $H^{0}_{W}(S, \mathbb Z(0)) =\mathbb Z$
,
$H^{0}_{W}(S, \mathbb Z(0)) =\mathbb Z$
,
![]() $H^{1}_{W}(S, \mathbb Z(0)) =0$
(up to a finite
$H^{1}_{W}(S, \mathbb Z(0)) =0$
(up to a finite
![]() $2$
-group) and
$2$
-group) and
![]() $H^{3}_{W}(S, \mathbb Z(0)) = \mu _{F}^{\vee }$
, the dual of the roots of unity in F.
$H^{3}_{W}(S, \mathbb Z(0)) = \mu _{F}^{\vee }$
, the dual of the roots of unity in F.
There is also an exact sequence
Note that
![]() $t_{M_{j}}=0$
for all j.
$t_{M_{j}}=0$
for all j.
![]() $\chi _{B}(S,0)=1$
: The sequence
$\chi _{B}(S,0)=1$
: The sequence
![]() $B(j,0)$
is zero for all
$B(j,0)$
is zero for all
![]() $j \neq 0$
and we can arrange
$j \neq 0$
and we can arrange
![]() $\chi (B(0,0)) =1$
by using the isomorphism
$\chi (B(0,0)) =1$
by using the isomorphism
 $$ \begin{align*} B(0,0):\qquad \textrm{Ker} (\gamma_{M_{0}}) \xrightarrow{\sim} H^{0}_{B}(S_{\mathbb C}, \mathbb Z(0))_{\mathbb C}^{+}\end{align*} $$
$$ \begin{align*} B(0,0):\qquad \textrm{Ker} (\gamma_{M_{0}}) \xrightarrow{\sim} H^{0}_{B}(S_{\mathbb C}, \mathbb Z(0))_{\mathbb C}^{+}\end{align*} $$
to transfer the integral structure
![]() $H^{0}_{B}(S_{\mathbb C}, \mathbb Z(0))^{+}$
to
$H^{0}_{B}(S_{\mathbb C}, \mathbb Z(0))^{+}$
to
![]() $\textrm {Ker}(\gamma _{M_{0}})$
.
$\textrm {Ker}(\gamma _{M_{0}})$
.
Since
![]() $A(j,r)$
contributes only for
$A(j,r)$
contributes only for
![]() $j \le 2r-3 =-3$
, it follows that there is no contribution from any of the
$j \le 2r-3 =-3$
, it follows that there is no contribution from any of the
![]() $A(j,0)$
-terms. We see that
$A(j,0)$
-terms. We see that
![]() $A^{\prime }(j,0) =0$
unless
$A^{\prime }(j,0) =0$
unless
![]() $j=1$
, in which case
$j=1$
, in which case
![]() $A^{\prime }(1,0) = \mu _{F}^{\vee }$
in degree 2. Thus, we obtain
$A^{\prime }(1,0) = \mu _{F}^{\vee }$
in degree 2. Thus, we obtain
![]() $\chi (A^{\prime }(1,0)) = w$
and
$\chi (A^{\prime }(1,0)) = w$
and
 $$ \begin{align*}\chi_{A^{\prime}}(S,0) = \frac{1}{w}.\end{align*} $$
$$ \begin{align*}\chi_{A^{\prime}}(S,0) = \frac{1}{w}.\end{align*} $$
The sequence
![]() $C(0)_{\mathbb C}$
for
$C(0)_{\mathbb C}$
for
![]() $V=S$
$V=S$
becomes the sequence (our convention is that
![]() $\textrm {Ker}(\gamma )$
has even degree, say, degree 2)
$\textrm {Ker}(\gamma )$
has even degree, say, degree 2)
 $$ \begin{align} 0 \to \underset{\textrm{degree 1}}{\mathbb C} \to \underset{\textrm{degree 2}}{\mathbb C^{r_{1}+r_{2}}} \to \underset{\textrm{degree 3}}{\textrm{Hom}(\mathcal O_{F}^{\times}, \mathbb C)} \to 0, \end{align} $$
$$ \begin{align} 0 \to \underset{\textrm{degree 1}}{\mathbb C} \to \underset{\textrm{degree 2}}{\mathbb C^{r_{1}+r_{2}}} \to \underset{\textrm{degree 3}}{\textrm{Hom}(\mathcal O_{F}^{\times}, \mathbb C)} \to 0, \end{align} $$
with
![]() $H^{2}_{W}(S, \mathbb Z(0))$
providing the standard integral structure
$H^{2}_{W}(S, \mathbb Z(0))$
providing the standard integral structure
![]() $\textrm {Hom}(\mathcal O_{F}^{\times }, \mathbb Z)$
on the last term and the second map being the dual of the classical regulator. So
$\textrm {Hom}(\mathcal O_{F}^{\times }, \mathbb Z)$
on the last term and the second map being the dual of the classical regulator. So
![]() $\chi (C(0)) = hR$
and so
$\chi (C(0)) = hR$
and so
 $$ \begin{align*} \chi(S,0) = \frac{\chi_{A,C}(S,0)}{\chi_{B}(S,0)} = \frac{\chi(C(0))~\cdot~\chi_{A^{\prime}}(S,0)}{1} = \frac{hR}{w}.\end{align*} $$
$$ \begin{align*} \chi(S,0) = \frac{\chi_{A,C}(S,0)}{\chi_{B}(S,0)} = \frac{\chi(C(0))~\cdot~\chi_{A^{\prime}}(S,0)}{1} = \frac{hR}{w}.\end{align*} $$
As is well-known,
So the conjectural formula (1) from [Reference Lichtenbaum27, Conjecture 3.1] is valid in this case.
2.7.2 The case
 $r=1$
$r=1$
The motives are
![]() $M_{j}=h^{j}(S)(1)$
.
$M_{j}=h^{j}(S)(1)$
.
As
![]() $A(j,1)$
contribute only for
$A(j,1)$
contribute only for
![]() $j <-1$
, we have
$j <-1$
, we have
![]() $\chi _{A}(S,1) =1$
. The complex
$\chi _{A}(S,1) =1$
. The complex
![]() $C(1)_{\mathbb C}$
(our convention is that
$C(1)_{\mathbb C}$
(our convention is that
![]() $\textrm {Coker}(\gamma )$
has odd degree, say 1)
$\textrm {Coker}(\gamma )$
has odd degree, say 1)
becomes
 $$ \begin{align}0 \to \underset{\textrm{degree 0 }}{\mathcal O_{F}^{\times}\otimes\mathbb C} \to \underset{\textrm{degree 1}}{\mathbb C^{r_{1}+r_{2}}} \to \underset{\textrm{degree 2 }}{\mathbb C} \to 0,\end{align} $$
$$ \begin{align}0 \to \underset{\textrm{degree 0 }}{\mathcal O_{F}^{\times}\otimes\mathbb C} \to \underset{\textrm{degree 1}}{\mathbb C^{r_{1}+r_{2}}} \to \underset{\textrm{degree 2 }}{\mathbb C} \to 0,\end{align} $$
with the last two terms getting the standard basis and the first term a basis from
![]() $\mathcal O_{F}^{\times }$
. This is exactly as in [Reference Lichtenbaum27, §7]. Thus,
$\mathcal O_{F}^{\times }$
. This is exactly as in [Reference Lichtenbaum27, §7]. Thus,
![]() $det(C(1))$
is the classical regulator R. One checks that
$det(C(1))$
is the classical regulator R. One checks that
![]() $H^{i}_{W}(S, \mathbb Z(1)) =0$
for
$H^{i}_{W}(S, \mathbb Z(1)) =0$
for
![]() $i> 3$
and that
$i> 3$
and that
![]() $H^{3}_{W}(S, \mathbb Z(1)) = \textrm {Hom}(H^{0}_{et}(S, \mathbb Z(0)), \mathbb Z)$
. As
$H^{3}_{W}(S, \mathbb Z(1)) = \textrm {Hom}(H^{0}_{et}(S, \mathbb Z(0)), \mathbb Z)$
. As
![]() $H^{i}_{W}(S,\mathbb Z(1)) = H^{i}_{et}(S, \mathbb Z(1))$
for
$H^{i}_{W}(S,\mathbb Z(1)) = H^{i}_{et}(S, \mathbb Z(1))$
for
![]() $i \le 2$
, this completes the computation of
$i \le 2$
, this completes the computation of
![]() $H^{*}_{W}(S, \mathbb Z(1))$
. From this, we see that
$H^{*}_{W}(S, \mathbb Z(1))$
. From this, we see that
 $$ \begin{align*}\chi (C(1)) = \frac{hR}{w}.\end{align*} $$
$$ \begin{align*}\chi (C(1)) = \frac{hR}{w}.\end{align*} $$
We need to consider
![]() $A^{\prime }(j,1)$
only when
$A^{\prime }(j,1)$
only when
![]() $j \ge 3$
. Since
$j \ge 3$
. Since
![]() $t_{M_{j}} =0$
for
$t_{M_{j}} =0$
for
![]() $j>0$
and
$j>0$
and
 $H^{j+2}_{W}(S, \mathbb Z(1)) =0$
for
$H^{j+2}_{W}(S, \mathbb Z(1)) =0$
for
![]() $j\ge 3$
, we see
$j\ge 3$
, we see
![]() $A^{\prime }(j,1) =0$
for
$A^{\prime }(j,1) =0$
for
![]() $j\ge 3$
. As a result,
$j\ge 3$
. As a result,
![]() $\chi _{A^{\prime }}(S,1)=1$
.
$\chi _{A^{\prime }}(S,1)=1$
.
Finally,
![]() $B(j,1) =0$
if
$B(j,1) =0$
if
![]() $j \neq 0$
and
$j \neq 0$
and
![]() $B(0,1)$
given by
$B(0,1)$
given by
 $$ \begin{align*}0\to H^0_B(S_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \to t_{M_0} \to \textrm{Coker}(\gamma_{M_0}) \to 0\end{align*} $$
$$ \begin{align*}0\to H^0_B(S_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \to t_{M_0} \to \textrm{Coker}(\gamma_{M_0}) \to 0\end{align*} $$
becomes (our convention is that
![]() $\textrm {Coker}(\gamma )$
has odd degree)
$\textrm {Coker}(\gamma )$
has odd degree)
 $$ \begin{align*}0 \to \underset{\textrm{degree 1 }}{\mathbb C^{r_{2}}} \to \underset{\textrm{degree 2 }}{\mathcal O_{F}\otimes_{\mathbb Z}\mathbb C} \to \underset{\textrm{degree 3 }}{\mathbb C^{r_{1}+r_{2}}} \to 0.\end{align*} $$
$$ \begin{align*}0 \to \underset{\textrm{degree 1 }}{\mathbb C^{r_{2}}} \to \underset{\textrm{degree 2 }}{\mathcal O_{F}\otimes_{\mathbb Z}\mathbb C} \to \underset{\textrm{degree 3 }}{\mathbb C^{r_{1}+r_{2}}} \to 0.\end{align*} $$
The first map is the composition of the natural inclusion of
![]() $\mathbb C^{r_{2}}$
in
$\mathbb C^{r_{2}}$
in
![]() $\mathbb C^{r_{1}+2r_{2}}$
(multiplied by
$\mathbb C^{r_{1}+2r_{2}}$
(multiplied by
![]() $2\pi i$
) with the inverse of
$2\pi i$
) with the inverse of
![]() $\psi $
of (6). The integral structure on
$\psi $
of (6). The integral structure on
![]() $\textrm {Coker}(\gamma _{M_{0}}) \cong \mathbb C^{r_{1}+r_{2}}$
is defined by
$\textrm {Coker}(\gamma _{M_{0}}) \cong \mathbb C^{r_{1}+r_{2}}$
is defined by
![]() $H^{0}_{B}(S, \mathbb Z(1))^{-} \cong \mathbb Z^{r_{1}+r_{2}}$
. Since the determinant of
$H^{0}_{B}(S, \mathbb Z(1))^{-} \cong \mathbb Z^{r_{1}+r_{2}}$
. Since the determinant of
![]() $\psi $
with respect to the usual bases is
$\psi $
with respect to the usual bases is
![]() $\sqrt {d}_{F}$
and the integral structures are torsion-free, we obtain
$\sqrt {d}_{F}$
and the integral structures are torsion-free, we obtain
 $$ \begin{align*} det (B(0,1)) = \frac{\sqrt{d_{F}}}{(2\pi i)^{r_{2}}} = \chi(B(0,1)).\end{align*} $$
$$ \begin{align*} det (B(0,1)) = \frac{\sqrt{d_{F}}}{(2\pi i)^{r_{2}}} = \chi(B(0,1)).\end{align*} $$
Hence, we obtain
 $$ \begin{align*}\chi(S,1) =\frac{\chi(C(1))}{\chi(B(0,1))} = \frac{hR(2\pi i)^{r_{2}}}{w\sqrt{d_{F}}};\end{align*} $$
$$ \begin{align*}\chi(S,1) =\frac{\chi(C(1))}{\chi(B(0,1))} = \frac{hR(2\pi i)^{r_{2}}}{w\sqrt{d_{F}}};\end{align*} $$
as the sign of
![]() $d_{F}$
is
$d_{F}$
is
![]() $(-1)^{r_{2}}$
, this is equal to the usual formula (up to a power of 2)
$(-1)^{r_{2}}$
, this is equal to the usual formula (up to a power of 2)
 $$ \begin{align} \zeta^{*}(S,1) = \frac{2^{r_{1}}h R(2\pi)^{r_{2}}}{w\sqrt{|d_{F}|}}.\end{align} $$
$$ \begin{align} \zeta^{*}(S,1) = \frac{2^{r_{1}}h R(2\pi)^{r_{2}}}{w\sqrt{|d_{F}|}}.\end{align} $$
So the conjectural formula (1) from [Reference Lichtenbaum27, Conjecture 3.1] is valid in this case, too.
2.8 The case of arithmetic surfaces:
 $V=X$
and
$V=X$
and
 $r=1$
$r=1$
We now turn to an explicit description of the terms that enter into the description of
![]() $\zeta ^{*}(X,1)$
; this uses the motives
$\zeta ^{*}(X,1)$
; this uses the motives
![]() $M_{j} = h^{j}(X_{0})(1)$
for
$M_{j} = h^{j}(X_{0})(1)$
for
![]() $j=0,1,2$
of the algebraic curve
$j=0,1,2$
of the algebraic curve
![]() $X_{0}$
over F and
$X_{0}$
over F and
 $t_{M_{j}} = H^{j}(X_{0}, \mathcal O_{X})$
. We begin with the Weil-étale motivic cohomology groups of X.
$t_{M_{j}} = H^{j}(X_{0}, \mathcal O_{X})$
. We begin with the Weil-étale motivic cohomology groups of X.
2.8.1 The groups
 $H^{*}_{W}(X,\mathbb Z(1))$
$H^{*}_{W}(X,\mathbb Z(1))$
Fix an arithmetic surface
![]() $\pi :X\to S$
.
$\pi :X\to S$
.
Since the motivic complex
![]() $\mathbb Z(1)$
is
$\mathbb Z(1)$
is
![]() $ \mathbb G_{m}[-1]$
, one has the identifications
$ \mathbb G_{m}[-1]$
, one has the identifications
 $$ \begin{align*}H^{j}_{et}(X, \mathbb Z(1)) = H^{j-1}_{et}(X, \mathbb G_{m}),\end{align*} $$
$$ \begin{align*}H^{j}_{et}(X, \mathbb Z(1)) = H^{j-1}_{et}(X, \mathbb G_{m}),\end{align*} $$
the Picard group
![]() $\textrm {Pic}(X) = H^{2}_{et}(X, \mathbb Z(1))$
and the Brauer group
$\textrm {Pic}(X) = H^{2}_{et}(X, \mathbb Z(1))$
and the Brauer group
![]() $\textrm {Br}(X) = H^{3}_{et}(X, \mathbb Z(1))$
.
$\textrm {Br}(X) = H^{3}_{et}(X, \mathbb Z(1))$
.
Recall that
![]() $H^{i}_{W}(X, \mathbb Z(1))$
[Reference Lichtenbaum27, §2.1] are defined as étale motivic cohomology
$H^{i}_{W}(X, \mathbb Z(1))$
[Reference Lichtenbaum27, §2.1] are defined as étale motivic cohomology
![]() $H^{i}_{et}(X, \mathbb Z(1))$
for
$H^{i}_{et}(X, \mathbb Z(1))$
for
![]() $i \le 2$
and, for
$i \le 2$
and, for
![]() $i>2$
, as the dual of étale motivic cohomology
$i>2$
, as the dual of étale motivic cohomology
thereby sitting in an exact sequence (for
![]() $i>2$
)
$i>2$
)
 $$ \begin{align*}0 \to \textrm{Ext}^{1}(H^{6-i}_{et}(X, \mathbb Z(1)), \mathbb Z) \to H^{i}_{W}(X, \mathbb Z(1)) \to \textrm{Hom}(H^{5-i}_{et}(X, \mathbb Z(1)), \mathbb Z) \to 0.\end{align*} $$
$$ \begin{align*}0 \to \textrm{Ext}^{1}(H^{6-i}_{et}(X, \mathbb Z(1)), \mathbb Z) \to H^{i}_{W}(X, \mathbb Z(1)) \to \textrm{Hom}(H^{5-i}_{et}(X, \mathbb Z(1)), \mathbb Z) \to 0.\end{align*} $$
As
![]() $H^{i}_{W}(X, \mathbb Z(1)) =0$
for
$H^{i}_{W}(X, \mathbb Z(1)) =0$
for
![]() $i=0$
and
$i=0$
and
![]() $i \ge 6$
, the following is a complete description of
$i \ge 6$
, the following is a complete description of
![]() $H^{*}_{W}(X, \mathbb Z(1))$
:
$H^{*}_{W}(X, \mathbb Z(1))$
:
 $$ \begin{align} H^{1}_{W}(X, \mathbb Z(1)) = {{\mathcal O}_{F}}^{\times}, \quad H^{2}_{W}(X, \mathbb Z(1)) = \textrm{Pic}(X), \quad H^{5}_{W}(X, \mathbb Z(1)) = \textrm{Ext}^{1}({\mathcal O_{F}}^{\times}, {\mathbb Z}), \end{align} $$
$$ \begin{align} H^{1}_{W}(X, \mathbb Z(1)) = {{\mathcal O}_{F}}^{\times}, \quad H^{2}_{W}(X, \mathbb Z(1)) = \textrm{Pic}(X), \quad H^{5}_{W}(X, \mathbb Z(1)) = \textrm{Ext}^{1}({\mathcal O_{F}}^{\times}, {\mathbb Z}), \end{align} $$
 $$ \begin{align} 0 \to \textrm{Ext}^{1}(\textrm{Br}(X), {\mathbb Z}) \to H^{3}_{W}(X, \mathbb Z(1)) \to \textrm{Hom}(\textrm{Pic}(X), \mathbb Z) \to 0, \end{align} $$
$$ \begin{align} 0 \to \textrm{Ext}^{1}(\textrm{Br}(X), {\mathbb Z}) \to H^{3}_{W}(X, \mathbb Z(1)) \to \textrm{Hom}(\textrm{Pic}(X), \mathbb Z) \to 0, \end{align} $$
 $$ \begin{align} 0 \to \textrm{Ext}^{1}(\textrm{Pic}(X), {\mathbb Z}) \to H^{4}_{W}(X, \mathbb Z(1)) \to \textrm{Hom}(\mathcal O_{F}^{\times}, \mathbb Z) \to 0.\end{align} $$
$$ \begin{align} 0 \to \textrm{Ext}^{1}(\textrm{Pic}(X), {\mathbb Z}) \to H^{4}_{W}(X, \mathbb Z(1)) \to \textrm{Hom}(\mathcal O_{F}^{\times}, \mathbb Z) \to 0.\end{align} $$
Remark. As the finite generation of
![]() $\textrm {Pic}(X)$
is well-known (theorem of Mordell–Weil–Roquette), the finite generation of
$\textrm {Pic}(X)$
is well-known (theorem of Mordell–Weil–Roquette), the finite generation of
![]() $H^{*}_{W}(X,\mathbb Z(1))$
reduces to the finiteness of
$H^{*}_{W}(X,\mathbb Z(1))$
reduces to the finiteness of
![]() $\textrm {Br}(X)$
.
$\textrm {Br}(X)$
.
2.8.2 The complexes
 $A(j,1)$
and
$A(j,1)$
and
 $A^{\prime }(j,1)$
$A^{\prime }(j,1)$
In our case, only
![]() $A^{\prime }(3,1)$
could be nonzero.
$A^{\prime }(3,1)$
could be nonzero.
In our case,
![]() $r=1$
. For
$r=1$
. For
![]() $A(j,1)$
to intervene, one needs
$A(j,1)$
to intervene, one needs
![]() $j\le 2r-3 =-1$
as
$j\le 2r-3 =-1$
as
![]() $2d-1=3$
. Since
$2d-1=3$
. Since
![]() $H^{0}_{W}(X,\mathbb Z(1)) =0$
, we obtain
$H^{0}_{W}(X,\mathbb Z(1)) =0$
, we obtain
![]() $\chi (A(j,1)=1)$
for all j.
$\chi (A(j,1)=1)$
for all j.
For
![]() $A^{\prime }(j,1)$
to intervene, one needs
$A^{\prime }(j,1)$
to intervene, one needs
![]() $j \ge 3$
. For
$j \ge 3$
. For
![]() $j=3$
, since
$j=3$
, since
![]() $H^{5}_{W}(X,\mathbb Z(1))$
is a finite group of order w, we have
$H^{5}_{W}(X,\mathbb Z(1))$
is a finite group of order w, we have
![]() $det(A^{\prime }(3,1)) =1$
and
$det(A^{\prime }(3,1)) =1$
and
![]() $\chi (A^{\prime }(3,1)) =w$
. If
$\chi (A^{\prime }(3,1)) =w$
. If
![]() $j>3$
, then
$j>3$
, then
 $H^{j+2}_{W}(X, \mathbb Z(1)) =0$
and
$H^{j+2}_{W}(X, \mathbb Z(1)) =0$
and
![]() $M_{j} =0$
; so
$M_{j} =0$
; so
![]() $\chi (A^{\prime }(j,1)) =1$
for
$\chi (A^{\prime }(j,1)) =1$
for
![]() $j>3$
. Thus,
$j>3$
. Thus,
 $$ \begin{align} \chi_{A}(X,1) =1, \qquad \chi_{A^{\prime}}(X,1) = \frac{1}{w}.\end{align} $$
$$ \begin{align} \chi_{A}(X,1) =1, \qquad \chi_{A^{\prime}}(X,1) = \frac{1}{w}.\end{align} $$
2.8.3 The groups
 $H^{i}(X, \mathcal O_{X})$
$H^{i}(X, \mathcal O_{X})$
Since
![]() $\pi :X \to S$
is proper,
$\pi :X \to S$
is proper,
![]() $H^{i}(X, \mathcal O_{X})$
are finitely generated
$H^{i}(X, \mathcal O_{X})$
are finitely generated
![]() $\mathcal O_{F}$
-modules.
$\mathcal O_{F}$
-modules.
Lemma 15.
![]() $H^{i}(X, \mathcal O_{X})$
is zero for
$H^{i}(X, \mathcal O_{X})$
is zero for
![]() $i\ge 2$
.
$i\ge 2$
.
Proof. Since
![]() $X\to S$
is a relative curve,
$X\to S$
is a relative curve,
![]() $H^{i}(X_{s}, \mathcal O_{X_{s}}) =0$
(for
$H^{i}(X_{s}, \mathcal O_{X_{s}}) =0$
(for
![]() $i>1$
) at all points
$i>1$
) at all points
![]() $s\in S$
. Since S is a reduced noetherian scheme and
$s\in S$
. Since S is a reduced noetherian scheme and
![]() $\pi : X\to S$
is proper and
$\pi : X\to S$
is proper and
![]() $\mathcal O_{X}$
is a coherent sheaf on X flat over S, by Grothendieck’s theorem on formal functions (see L. Illusie’s article [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli9, Corollary 8.3.4]),
$\mathcal O_{X}$
is a coherent sheaf on X flat over S, by Grothendieck’s theorem on formal functions (see L. Illusie’s article [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli9, Corollary 8.3.4]),
![]() $R^{i}\pi _{*}\mathcal O_{X} =0$
for
$R^{i}\pi _{*}\mathcal O_{X} =0$
for
![]() $i>1$
.
$i>1$
.
Using Subsection 2.8.2 and Lemma 15, we find that
 $$ \begin{align} \chi(X,1) = \frac{{\chi (C(1))}}{\chi(A^{\prime}(3,1))}~\cdot~\frac{\chi(B(1,1))}{\chi(B(0,1))} =\frac{{\chi (C(1))}}{w}~\cdot~\frac{\chi(B(1,1))}{\chi(B(0,1))},\end{align} $$
$$ \begin{align} \chi(X,1) = \frac{{\chi (C(1))}}{\chi(A^{\prime}(3,1))}~\cdot~\frac{\chi(B(1,1))}{\chi(B(0,1))} =\frac{{\chi (C(1))}}{w}~\cdot~\frac{\chi(B(1,1))}{\chi(B(0,1))},\end{align} $$
where the exact sequence
![]() $B(j,1)$
is
$B(j,1)$
is
 $$ \begin{align} 0 \to \textrm{Ker}(\gamma_{M_{j}}) \to H^{j}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \to t_{M_{j}} \to \textrm{Coker}(\gamma_{M_{j}}) \to 0 \end{align} $$
$$ \begin{align} 0 \to \textrm{Ker}(\gamma_{M_{j}}) \to H^{j}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \to t_{M_{j}} \to \textrm{Coker}(\gamma_{M_{j}}) \to 0 \end{align} $$
and
![]() $C(1)_{\mathbb C}$
is
$C(1)_{\mathbb C}$
is
 $$ \begin{align} 0 &\to H^{1}_{W}(X, \mathbb Z(1))_{\mathbb C} \to \textrm{Coker}(\gamma_{M_{0}}) \to H^{3}_{W}(X, \mathbb Z(1))_{\mathbb C} \to H^{2}_{W}(X, \mathbb Z(1))_{\mathbb C} \to \textrm{Ker}(\gamma_{M_{2}}) \nonumber\\[3pt] &\to H^{4}_{W}(X, \mathbb Z(1))_{\mathbb C} \to 0.\end{align} $$
$$ \begin{align} 0 &\to H^{1}_{W}(X, \mathbb Z(1))_{\mathbb C} \to \textrm{Coker}(\gamma_{M_{0}}) \to H^{3}_{W}(X, \mathbb Z(1))_{\mathbb C} \to H^{2}_{W}(X, \mathbb Z(1))_{\mathbb C} \to \textrm{Ker}(\gamma_{M_{2}}) \nonumber\\[3pt] &\to H^{4}_{W}(X, \mathbb Z(1))_{\mathbb C} \to 0.\end{align} $$
So Conjecture 1 provides an intrinsic formula for
![]() $\zeta ^{*}(X,1)$
using only
$\zeta ^{*}(X,1)$
using only
![]() $B(0,1)$
,
$B(0,1)$
,
![]() $B(1,1)$
,
$B(1,1)$
,
![]() $C(1)$
and
$C(1)$
and
![]() $H^{*}_{W}(X, \mathbb Z(1))$
. We compute
$H^{*}_{W}(X, \mathbb Z(1))$
. We compute
![]() $\chi (B(0,1))$
and explain how
$\chi (B(0,1))$
and explain how
![]() $\chi (B(2,1))$
can be assumed to be one.
$\chi (B(2,1))$
can be assumed to be one.
2.8.4
 $\chi (B(0,1))$
$\chi (B(0,1))$
This has been computed ([Reference Lichtenbaum27, §7]) in Subsection 2.7. Here
Our convention for
![]() $B(0,1)$
is that
$B(0,1)$
is that
![]() $\textrm {Coker}(\gamma _{M})$
is in odd degree, say, degree 3. As the integral structure
$\textrm {Coker}(\gamma _{M})$
is in odd degree, say, degree 3. As the integral structure
 $$ \begin{align*}B(0,1):\qquad 0 \to \underset{\textrm{degree 1 }}{H^{0}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}} \to \underset{\textrm{degree 2}}{(\mathcal O_{F})_{\mathbb C}} \to \underset{\textrm{degree 3}}{\textrm{Coker}(\gamma_{M_{0}})} \to 0\end{align*} $$
$$ \begin{align*}B(0,1):\qquad 0 \to \underset{\textrm{degree 1 }}{H^{0}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}} \to \underset{\textrm{degree 2}}{(\mathcal O_{F})_{\mathbb C}} \to \underset{\textrm{degree 3}}{\textrm{Coker}(\gamma_{M_{0}})} \to 0\end{align*} $$
is torsion-free, we have (again using that the sign of
![]() $d_{F}$
is
$d_{F}$
is
![]() $(-1)^{r_{2}}$
)
$(-1)^{r_{2}}$
)
 $$ \begin{align} \chi (B(0,1)) = det (B(0,1)) = \frac{\sqrt{d_{F}}}{(2\pi i)^{r_{2}}} = \frac{\sqrt{|d_{F}|}}{(2\pi)^{r_{2}}}.\end{align} $$
$$ \begin{align} \chi (B(0,1)) = det (B(0,1)) = \frac{\sqrt{d_{F}}}{(2\pi i)^{r_{2}}} = \frac{\sqrt{|d_{F}|}}{(2\pi)^{r_{2}}}.\end{align} $$
2.8.5 The sequence
 $B(2,1)$
$B(2,1)$
By Lemma 15,
![]() $t_{M_{2}} = H^{2}(X_{0}, \mathcal O) =0$
; so, in
$t_{M_{2}} = H^{2}(X_{0}, \mathcal O) =0$
; so, in
![]() $B(2,1)$
,
$B(2,1)$
,
 $$ \begin{align*} \textrm{Ker}(\gamma_{M_{2}}) \xrightarrow{\sim} H^{2}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C},\end{align*} $$
$$ \begin{align*} \textrm{Ker}(\gamma_{M_{2}}) \xrightarrow{\sim} H^{2}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C},\end{align*} $$
we use the isomorphism to transfer the integral structure from
![]() $H^{2}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}$
to
$H^{2}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}$
to
![]() $\textrm {Ker}(\gamma _{M_{2}})$
, thereby obtaining
$\textrm {Ker}(\gamma _{M_{2}})$
, thereby obtaining
3 The conjecture of Birch–Swinnerton–Dyer–Tate
3.1 Statement of the conjecture [Reference Tate36, Reference Gross19]
Our presentation of this conjecture follows (almost verbatim) [Reference Gross19, § 2] where it is formulated in terms of Néron models.
Let A be an abelian variety of dimension g over
![]() $\text {Spec}~F$
. Let
$\text {Spec}~F$
. Let
![]() $L(A,s)$
be its L-series over F, which is defined – see (28) by a Euler product convergent in the half-plane Re
$L(A,s)$
be its L-series over F, which is defined – see (28) by a Euler product convergent in the half-plane Re
 $(s)> \frac {3}{2}$
. We assume that
$(s)> \frac {3}{2}$
. We assume that
![]() $L(A,s)$
has an analytic continuation to the entire complex plane. We write
$L(A,s)$
has an analytic continuation to the entire complex plane. We write
![]() $L^{*}(A,1)$
for its special value at
$L^{*}(A,1)$
for its special value at
![]() $s=1$
. Write
$s=1$
. Write
 $$ \begin{align*} L(A,s)~\sim~~c~\cdot~(s-1)^{r(A)} \qquad s\to 1,\end{align*} $$
$$ \begin{align*} L(A,s)~\sim~~c~\cdot~(s-1)^{r(A)} \qquad s\to 1,\end{align*} $$
where
![]() $r(A)$
is a nonnegative integer and c is nonzero (the special value
$r(A)$
is a nonnegative integer and c is nonzero (the special value
![]() $L^{*}(A,1)$
). Birch and Swinnerton–Dyer and Tate have conjectured that
$L^{*}(A,1)$
). Birch and Swinnerton–Dyer and Tate have conjectured that
![]() $r(A)$
is equal to the rank of the finitely generated group
$r(A)$
is equal to the rank of the finitely generated group
![]() $A(F)$
of points of A over F; they have also given a conjectural formula for
$A(F)$
of points of A over F; they have also given a conjectural formula for
![]() $L^{*}(A,1)$
in terms of certain arithmetic invariants of A which we now recall.
$L^{*}(A,1)$
in terms of certain arithmetic invariants of A which we now recall.
Let
![]() $\mathcal N$
be the Néron model of A over S. Let
$\mathcal N$
be the Néron model of A over S. Let
![]() $\mathcal N^{0}$
be the largest open subgroup scheme of
$\mathcal N^{0}$
be the largest open subgroup scheme of
![]() $\mathcal N$
in which all fibres are connected. For any nonzero prime v of
$\mathcal N$
in which all fibres are connected. For any nonzero prime v of
![]() $\mathcal O_{F}$
(i.e.,
$\mathcal O_{F}$
(i.e.,
![]() $v \in S$
), we write
$v \in S$
), we write
for the fibres over v. Thus,
![]() $\mathcal N_{v}$
is a commutative group scheme over
$\mathcal N_{v}$
is a commutative group scheme over
![]() $k(v)$
and
$k(v)$
and
![]() $\mathcal N^{0}_{v}$
is the connected component of the identity of
$\mathcal N^{0}_{v}$
is the connected component of the identity of
![]() $\mathcal N_{v}$
. We have an exact sequence of group schemes over
$\mathcal N_{v}$
. We have an exact sequence of group schemes over
![]() $k(v)$
:
$k(v)$
:
where
![]() $H_{v}$
is a commutative linear group scheme and
$H_{v}$
is a commutative linear group scheme and
![]() $B_{v}$
is an abelian variety. For almost all v, we have
$B_{v}$
is an abelian variety. For almost all v, we have
these are the primes where A has good reduction. Let
![]() $Y_{v} = \textrm {Hom}(H_{v}, \mathbb G_{m})$
be the character group of
$Y_{v} = \textrm {Hom}(H_{v}, \mathbb G_{m})$
be the character group of
![]() $H_{v}$
and
$H_{v}$
and
![]() $\pi _{v}$
be the Frobenius endomorphism of
$\pi _{v}$
be the Frobenius endomorphism of
![]() $B_{v}$
.
$B_{v}$
.
We write
![]() $\Phi _{v}=\pi _{0}(\mathcal N_{v})$
for the finite group scheme of connected components of the fibre
$\Phi _{v}=\pi _{0}(\mathcal N_{v})$
for the finite group scheme of connected components of the fibre
![]() $\mathcal N_{v}$
over v. The Tamagawa number of A at v, denoted
$\mathcal N_{v}$
over v. The Tamagawa number of A at v, denoted
![]() $c_{v}$
, is the size of the group
$c_{v}$
, is the size of the group
![]() $\Phi _{v}(k(v))$
of the group of rational points of
$\Phi _{v}(k(v))$
of the group of rational points of
![]() $\Phi _{v}$
. The Tamagawa number
$\Phi _{v}$
. The Tamagawa number
![]() $c_{v}$
is one for almost all
$c_{v}$
is one for almost all
![]() $v \in S$
; we may define the product
$v \in S$
; we may define the product
 $$ \begin{align} P_{A, fin} = \prod_{v\in S} c_{v}.\end{align} $$
$$ \begin{align} P_{A, fin} = \prod_{v\in S} c_{v}.\end{align} $$
Let
![]() $\Gamma _{v}$
be a decomposition group for v in
$\Gamma _{v}$
be a decomposition group for v in
![]() $\Gamma _{F} = \textrm {Gal}(\bar {F}/F)$
and let
$\Gamma _{F} = \textrm {Gal}(\bar {F}/F)$
and let
![]() $I_{v}$
be the inertia subgroup of
$I_{v}$
be the inertia subgroup of
![]() $\Gamma _{v}$
and
$\Gamma _{v}$
and
![]() $\sigma _{v}$
be an arithmetic Frobenius, a topological generator of the quotient
$\sigma _{v}$
be an arithmetic Frobenius, a topological generator of the quotient
![]() $\Gamma _{v}/{I_{v}}$
. For any prime
$\Gamma _{v}/{I_{v}}$
. For any prime
![]() $\ell $
distinct from the characteristic of
$\ell $
distinct from the characteristic of
![]() $k(v)$
, consider the
$k(v)$
, consider the
![]() $\ell $
-adic Tate module
$\ell $
-adic Tate module
![]() $T_{\ell }A$
of A; this is a free
$T_{\ell }A$
of A; this is a free
![]() $\mathbb Z_{\ell }$
-module of rank
$\mathbb Z_{\ell }$
-module of rank
![]() $2g$
which admits a continuous
$2g$
which admits a continuous
![]() $\mathbb Z_{\ell }$
-linear action of
$\mathbb Z_{\ell }$
-linear action of
![]() $\Gamma _{F}$
. We define the local L-factor of A at v by the formula
$\Gamma _{F}$
. We define the local L-factor of A at v by the formula
The characteristic polynomial
![]() $L_{v}(A,t)$
has integral coefficients which are independent of
$L_{v}(A,t)$
has integral coefficients which are independent of
![]() $\ell $
: this is evident from the formula
$\ell $
: this is evident from the formula
where the first determinant is clearly independent of
![]() $\ell $
and the second is the characteristic polynomial of an endomorphism of the abelian variety
$\ell $
and the second is the characteristic polynomial of an endomorphism of the abelian variety
![]() $B_{v}$
which has integral coefficients independent of
$B_{v}$
which has integral coefficients independent of
![]() $\ell $
by a theorem of A. Weil.
$\ell $
by a theorem of A. Weil.
The roots of the first factor have complex absolute value 1, whereas those of the second factor have complex absolute value
 $q_{v}^{-1/2}$
. Therefore, the global L-series
$q_{v}^{-1/2}$
. Therefore, the global L-series
![]() $L(A,s)$
defined by
$L(A,s)$
defined by
 $$ \begin{align} L(A,s) = L(A/F,s) = \prod_{v\in S} \frac{1}{L_{v}(A, q_{v}^{-s})}\end{align} $$
$$ \begin{align} L(A,s) = L(A/F,s) = \prod_{v\in S} \frac{1}{L_{v}(A, q_{v}^{-s})}\end{align} $$
converges for Re
 $(s)>\frac {3}{2}$
. We shall assume that it has an analytic continuation to the entire complex plane.
$(s)>\frac {3}{2}$
. We shall assume that it has an analytic continuation to the entire complex plane.
3.2 The archimedean period of A
Let
![]() $\omega _{\mathcal N}$
denote the projective
$\omega _{\mathcal N}$
denote the projective
![]() $\mathcal O_{F}$
-module of invariant differentials of the Néron model
$\mathcal O_{F}$
-module of invariant differentials of the Néron model
![]() $\mathcal N$
. Since g is the rank of
$\mathcal N$
. Since g is the rank of
![]() $\omega _{\mathcal N}$
, the module
$\omega _{\mathcal N}$
, the module
![]() $\Lambda ^{g}\omega _{\mathcal N}$
is a rank 1
$\Lambda ^{g}\omega _{\mathcal N}$
is a rank 1
![]() $\mathcal O_{F}$
-submodule of
$\mathcal O_{F}$
-submodule of
![]() $H^{0}(A, \Omega ^{g})$
, a vector space over F of dimension 1. Let
$H^{0}(A, \Omega ^{g})$
, a vector space over F of dimension 1. Let
![]() $\{w_{1}, \cdots , w_{g}\}$
be an F-basis of
$\{w_{1}, \cdots , w_{g}\}$
be an F-basis of
![]() $H^{0}(A, \Omega ^{1})$
and put
$H^{0}(A, \Omega ^{1})$
and put
![]() $\eta = w_{1}\wedge \cdots \wedge w_{g}$
. We have
$\eta = w_{1}\wedge \cdots \wedge w_{g}$
. We have
 $$ \begin{align} \Lambda^{g}\omega_{\mathcal N} = \eta~\cdot~\mathfrak a_{\eta} \quad \subset H^{0}(A, \Omega^{g}) \end{align} $$
$$ \begin{align} \Lambda^{g}\omega_{\mathcal N} = \eta~\cdot~\mathfrak a_{\eta} \quad \subset H^{0}(A, \Omega^{g}) \end{align} $$
where
![]() $\mathfrak a_{\eta }$
is a fractional ideal of F and
$\mathfrak a_{\eta }$
is a fractional ideal of F and
For any
![]() $\sigma \in S_{\mathbb R}$
(corresponds to a real embedding
$\sigma \in S_{\mathbb R}$
(corresponds to a real embedding
![]() $\sigma : F \to \mathbb R$
), let
$\sigma : F \to \mathbb R$
), let
![]() $H^{+}$
denote the submodule of
$H^{+}$
denote the submodule of
![]() $H_{1}(A_{\sigma }(\mathbb C), \mathbb Z)$
which is fixed by complex conjugation; it is a free
$H_{1}(A_{\sigma }(\mathbb C), \mathbb Z)$
which is fixed by complex conjugation; it is a free
![]() $\mathbb Z$
-module of rank g and if
$\mathbb Z$
-module of rank g and if
![]() $\{ \gamma _{1}, \cdots , \gamma _{g}\}$
denotes a basis, we put
$\{ \gamma _{1}, \cdots , \gamma _{g}\}$
denotes a basis, we put
 $$ \begin{align} p_{\sigma} (A, \eta) = [(\pi_{0}(A_{\sigma}(\mathbb R)))]~\cdot~\Bigg|~\textrm{det} \bigg( \bigg(\int_{\gamma_{i}}\omega_{j} \bigg)\bigg)~\Bigg|.\end{align} $$
$$ \begin{align} p_{\sigma} (A, \eta) = [(\pi_{0}(A_{\sigma}(\mathbb R)))]~\cdot~\Bigg|~\textrm{det} \bigg( \bigg(\int_{\gamma_{i}}\omega_{j} \bigg)\bigg)~\Bigg|.\end{align} $$
For any complex place v of S (corresponding to
![]() $\sigma : F \to \mathbb C$
and its conjugate), let
$\sigma : F \to \mathbb C$
and its conjugate), let
![]() $\{\gamma _{1}, \cdots , \gamma _{2g}\}$
be a basis of the free module
$\{\gamma _{1}, \cdots , \gamma _{2g}\}$
be a basis of the free module
![]() $H_{1}(A_{\sigma }(\mathbb C), \mathbb Z)$
of rank
$H_{1}(A_{\sigma }(\mathbb C), \mathbb Z)$
of rank
![]() $2g$
and define the period
$2g$
and define the period
 $$ \begin{align} p_{\sigma} (A, \eta) = \big | \textrm{det}( M_{v}(A, \eta)) \big |, \qquad M_{v}(A, \eta) = \bigg(\bigg(\int_{\gamma_{i}}\omega_{j}, {\overline{{\int_{\gamma_{i}}{{\omega}_{j}}}}}~\bigg) \bigg)~;\end{align} $$
$$ \begin{align} p_{\sigma} (A, \eta) = \big | \textrm{det}( M_{v}(A, \eta)) \big |, \qquad M_{v}(A, \eta) = \bigg(\bigg(\int_{\gamma_{i}}\omega_{j}, {\overline{{\int_{\gamma_{i}}{{\omega}_{j}}}}}~\bigg) \bigg)~;\end{align} $$
this period is nonzero and depends only on the differential form
![]() $\eta $
and the place v. The period of A (relative to
$\eta $
and the place v. The period of A (relative to
![]() $\eta $
) is the real number
$\eta $
) is the real number
 $$ \begin{align} P_{A, \infty}(\eta) = \prod_{\sigma \in S_{\infty}} p_{\sigma}(A, \eta). \end{align} $$
$$ \begin{align} P_{A, \infty}(\eta) = \prod_{\sigma \in S_{\infty}} p_{\sigma}(A, \eta). \end{align} $$
Remark 16. We recall the well-known fact that the determinant of
![]() $M_{v}(A, \eta )$
is
$M_{v}(A, \eta )$
is
![]() $(\sqrt {-1})^{g}$
times a real number. In the basis
$(\sqrt {-1})^{g}$
times a real number. In the basis
![]() $\{\kappa _{1}, \cdots , \kappa _{g}\}$
of
$\{\kappa _{1}, \cdots , \kappa _{g}\}$
of
![]() $H^{0}(A_{\sigma }(\mathbb C), \Omega ^{1})$
defined by
$H^{0}(A_{\sigma }(\mathbb C), \Omega ^{1})$
defined by
 $\int _{\gamma _{j}}\kappa _{i} = \delta _{ij}$
for
$\int _{\gamma _{j}}\kappa _{i} = \delta _{ij}$
for
![]() $1\le i,j\le g$
, the
$1\le i,j\le g$
, the
![]() $2g\times 2g$
-period matrix
$2g\times 2g$
-period matrix
 $(\int _{\gamma _{i}}\kappa _{j}, {\overline {{\int _{\gamma _{i}} \kappa _{j}}}})$
is a block matrix of the form
$(\int _{\gamma _{i}}\kappa _{j}, {\overline {{\int _{\gamma _{i}} \kappa _{j}}}})$
is a block matrix of the form
 $$ \begin{align*}M^{\prime}= \begin{bmatrix} I_{g} & I_{g}\\ \Omega & {\overline{\Omega}} \end{bmatrix}, \qquad \Omega = \bigg(\int_{\gamma_{g+i}}\kappa_{j}\bigg)_{1\le i,j \le g} \end{align*} $$
$$ \begin{align*}M^{\prime}= \begin{bmatrix} I_{g} & I_{g}\\ \Omega & {\overline{\Omega}} \end{bmatrix}, \qquad \Omega = \bigg(\int_{\gamma_{g+i}}\kappa_{j}\bigg)_{1\le i,j \le g} \end{align*} $$
whose determinant is equal to the determinant of the
![]() $g \times g$
-matrix
$g \times g$
-matrix
![]() ${\overline {\Omega }} - \Omega $
(all of its entries have zero real part) and hence
${\overline {\Omega }} - \Omega $
(all of its entries have zero real part) and hence
![]() $\textrm {det}(M^{\prime })$
is the product of a real number with
$\textrm {det}(M^{\prime })$
is the product of a real number with
![]() $\sqrt {-1}^{g}$
. If K is the change of basis matrix from the basis
$\sqrt {-1}^{g}$
. If K is the change of basis matrix from the basis
![]() $\{w_{1}, \cdots , w_{g}\}$
to the basis
$\{w_{1}, \cdots , w_{g}\}$
to the basis
![]() $\{\kappa _{1}, \cdots , \kappa _{g}\}$
, then
$\{\kappa _{1}, \cdots , \kappa _{g}\}$
, then
 $$ \begin{align*} M_{v}(A, \eta) = M^{\prime}~\cdot~ \begin{bmatrix} K & 0\\ 0 & {\overline{K}} \end{bmatrix} \implies \textrm{det} (M_{v}(A, \eta)) = \textrm{det}(M^{\prime})~\cdot~\textrm{det}(K)~\cdot~{\overline{\textrm{det}(K)}}. \end{align*} $$
$$ \begin{align*} M_{v}(A, \eta) = M^{\prime}~\cdot~ \begin{bmatrix} K & 0\\ 0 & {\overline{K}} \end{bmatrix} \implies \textrm{det} (M_{v}(A, \eta)) = \textrm{det}(M^{\prime})~\cdot~\textrm{det}(K)~\cdot~{\overline{\textrm{det}(K)}}. \end{align*} $$
Lemma 17. The number
 $$ \begin{align*}P_{A, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) = \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})~\cdot~\prod_{v \in S_{\infty}} p_{v}(A,\eta)\end{align*} $$
$$ \begin{align*}P_{A, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) = \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})~\cdot~\prod_{v \in S_{\infty}} p_{v}(A,\eta)\end{align*} $$
is independent of
![]() $\eta $
. It will be denoted
$\eta $
. It will be denoted
![]() $P_{A, \infty }$
.
$P_{A, \infty }$
.
Proof. For any
![]() $0 \neq k \in F$
and any
$0 \neq k \in F$
and any
![]() $v \in S_{\infty }$
, one has
$v \in S_{\infty }$
, one has
 $$ \begin{align*} p_{v}(A, k\eta)= \begin{cases} p_{v}(A, \eta)~\cdot~\sigma(k)& \mbox{if}~v\in S_{\mathbb R}\\ p_{v}(A, \eta)~\cdot~\overline{\sigma(k)}~\cdot~\sigma(k)&\mbox{if}~v\in S_{\mathbb C} \end{cases}.\end{align*} $$
$$ \begin{align*} p_{v}(A, k\eta)= \begin{cases} p_{v}(A, \eta)~\cdot~\sigma(k)& \mbox{if}~v\in S_{\mathbb R}\\ p_{v}(A, \eta)~\cdot~\overline{\sigma(k)}~\cdot~\sigma(k)&\mbox{if}~v\in S_{\mathbb C} \end{cases}.\end{align*} $$
On the other hand, we see from (30) that
![]() $\mathfrak a_{k\eta } = (k)^{-1} \mathfrak a_{\eta }$
. Since
$\mathfrak a_{k\eta } = (k)^{-1} \mathfrak a_{\eta }$
. Since
 $$ \begin{align} \prod_{\sigma \in \tilde{S}} \sigma(k) = \mathbb N_{F/{\mathbb Q}}(k),\end{align} $$
$$ \begin{align} \prod_{\sigma \in \tilde{S}} \sigma(k) = \mathbb N_{F/{\mathbb Q}}(k),\end{align} $$
one has
 $$ \begin{align*} \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{k\eta}) & \cdot~\prod_{\sigma \in S_{\infty}} p_{\sigma}(A,k\eta) = \mathbb N_{F/{\mathbb Q}}(k)^{-1}~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) ~\cdot~\prod_{\sigma \in S_{\infty}} p_{\sigma}(A,\eta) \nonumber \\[3pt] &\cdot~(\prod_{\sigma \in \tilde{S}} \sigma(k)) = \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) ~\cdot~\prod_{\sigma \in {S}_{\infty} } p_{\sigma}(A,\eta). \\[-40pt] \end{align*} $$
$$ \begin{align*} \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{k\eta}) & \cdot~\prod_{\sigma \in S_{\infty}} p_{\sigma}(A,k\eta) = \mathbb N_{F/{\mathbb Q}}(k)^{-1}~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) ~\cdot~\prod_{\sigma \in S_{\infty}} p_{\sigma}(A,\eta) \nonumber \\[3pt] &\cdot~(\prod_{\sigma \in \tilde{S}} \sigma(k)) = \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) ~\cdot~\prod_{\sigma \in {S}_{\infty} } p_{\sigma}(A,\eta). \\[-40pt] \end{align*} $$
Definition 18. The global volume
![]() $P_{A}$
of A is defined by
$P_{A}$
of A is defined by
 $$ \begin{align*} P_{A} = \frac{P_{A, fin}~\cdot~P_{A, \infty}}{|d_{F}|^{g/2}} = \frac{P_{A, fin}~\cdot~P_{A, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) }{|d_{F}|^{g/2}}.\end{align*} $$
$$ \begin{align*} P_{A} = \frac{P_{A, fin}~\cdot~P_{A, \infty}}{|d_{F}|^{g/2}} = \frac{P_{A, fin}~\cdot~P_{A, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) }{|d_{F}|^{g/2}}.\end{align*} $$
Remark 19. It is known that
![]() $P_{A}$
is the volume
$P_{A}$
is the volume
![]() $m_{A}(A(\mathbb A_{F}))$
of the adelic points
$m_{A}(A(\mathbb A_{F}))$
of the adelic points
![]() $A(\mathbb A_{F})$
with respect to the (canonical) Tamagawa measure
$A(\mathbb A_{F})$
with respect to the (canonical) Tamagawa measure
![]() $m_{A}$
. If
$m_{A}$
. If
![]() $A^{\prime }$
is the Weil restriction of A to
$A^{\prime }$
is the Weil restriction of A to
![]() $F^{\prime }\subset F$
, then
$F^{\prime }\subset F$
, then
![]() $L(A,s) = L(A^{\prime },s)$
. One can compare the terms in Conjecture 20 for A and
$L(A,s) = L(A^{\prime },s)$
. One can compare the terms in Conjecture 20 for A and
![]() $A^{\prime }$
:
$A^{\prime }$
:
see Remark 23 for the the comparison of
![]() $P_{A}$
and
$P_{A}$
and
![]() $P_{A^{\prime }}$
. Conjecture 20 is compatible with restriction of scalars [Reference Milne33] [Reference Conrad7, §6]: Conjecture 20 for A over F is equivalent to
$P_{A^{\prime }}$
. Conjecture 20 is compatible with restriction of scalars [Reference Milne33] [Reference Conrad7, §6]: Conjecture 20 for A over F is equivalent to
![]() $A^{\prime }$
over
$A^{\prime }$
over
![]() $F^{\prime }$
; see [Reference Conrad7, §6] for a beautiful exposition.
$F^{\prime }$
; see [Reference Conrad7, §6] for a beautiful exposition.
Let
![]() $A^{t}$
be the dual abelian variety. We write
$A^{t}$
be the dual abelian variety. We write
![]() $\Theta _{NT}(A)$
for the determinant of the Néron–Tate height pairing
$\Theta _{NT}(A)$
for the determinant of the Néron–Tate height pairing
 $$ \begin{align} \frac{A(F)}{A(F)_{tor}} \times \frac{A^{t}(F)}{A^{t}(F)_{tor}} \to \mathbb R. \end{align} $$
$$ \begin{align} \frac{A(F)}{A(F)_{tor}} \times \frac{A^{t}(F)}{A^{t}(F)_{tor}} \to \mathbb R. \end{align} $$
Since this height pairing corresponds to the Poincaré divisor on
![]() $A \times A^{t}$
which is symmetric, it follows that
$A \times A^{t}$
which is symmetric, it follows that
![]() $\Theta _{NT}(A) = \Theta _{NT}(A^{t})$
. Following Subsection 2.3.5, one has
$\Theta _{NT}(A) = \Theta _{NT}(A^{t})$
. Following Subsection 2.3.5, one has
 $$ \begin{align*} \Delta_{NT}(A) = \frac{\Theta_{NT}(A)}{([A(F)_{tor}]~\cdot~[A^{t}(F)_{tor}])}.\end{align*} $$
$$ \begin{align*} \Delta_{NT}(A) = \frac{\Theta_{NT}(A)}{([A(F)_{tor}]~\cdot~[A^{t}(F)_{tor}])}.\end{align*} $$
Finally, let
![]() denote the Tate–Shafarevich group of A over F.
denote the Tate–Shafarevich group of A over F.
The BSD conjecture states that the order of vanishing of
![]() $L(A,s)$
at
$L(A,s)$
at
![]() $s=1$
is equal to the rank of the Mordell–Weil group
$s=1$
is equal to the rank of the Mordell–Weil group
![]() $A(F)$
of A. The strong BSD conjecture [Reference Tate36] (we follow Gross’s formulation [Reference Gross19, Conjecture 2.10] which is shown by him to be equivalent to the one in [Reference Tate36]) concerns the special value
$A(F)$
of A. The strong BSD conjecture [Reference Tate36] (we follow Gross’s formulation [Reference Gross19, Conjecture 2.10] which is shown by him to be equivalent to the one in [Reference Tate36]) concerns the special value
![]() $L^{*}(A,1)$
of
$L^{*}(A,1)$
of
![]() $L(A,s)$
at
$L(A,s)$
at
![]() $s=1$
.
$s=1$
.
Conjecture 20.
![]() is finite and
is finite and
![]() $L^{*}(A,1)$
satisfies
$L^{*}(A,1)$
satisfies

3.3 The case of everywhere good reduction
If A has good reduction everywhere, then
![]() $c_{v}=1$
for all
$c_{v}=1$
for all
![]() $v \in S$
and
$v \in S$
and
![]() $P_{A,fin} =1$
; also,
$P_{A,fin} =1$
; also,
![]() $A_{v} = \mathcal N_{v} = \mathcal N^{0}_{v} = B_{v}.$
Conjecture 20 simplifies to the following.
$A_{v} = \mathcal N_{v} = \mathcal N^{0}_{v} = B_{v}.$
Conjecture 20 simplifies to the following.
Conjecture 21. If A has good reduction everywhere, then

4 Comparison of periods
In order to relate Conjectures 1 and 20, it is necessary to compare the period
![]() $P_{J, \infty }$
of Lemma 17 with the determinant of
$P_{J, \infty }$
of Lemma 17 with the determinant of
![]() $B(1,1)$
in (21). Let
$B(1,1)$
in (21). Let
![]() $\omega _{\mathcal J}$
denote the projective
$\omega _{\mathcal J}$
denote the projective
![]() $\mathcal O_{F}$
-module of invariant differentials on the Néron model
$\mathcal O_{F}$
-module of invariant differentials on the Néron model
![]() $\mathcal J$
of the Jacobian J of
$\mathcal J$
of the Jacobian J of
![]() $X_{0}$
. Recall that the integral structure
$X_{0}$
. Recall that the integral structure
![]() $i_{\omega _{\mathcal J}}$
(Definition 5) uses the abelian group underlying
$i_{\omega _{\mathcal J}}$
(Definition 5) uses the abelian group underlying
![]() $\omega _{\mathcal J}$
and forgets the
$\omega _{\mathcal J}$
and forgets the
![]() $\mathcal O_{F}$
-structure.
$\mathcal O_{F}$
-structure.
Definition 22. (i)
![]() $det(\gamma _{\mathcal J}^{*})$
is the determinant of the period isomorphism
$det(\gamma _{\mathcal J}^{*})$
is the determinant of the period isomorphism
 $$ \begin{align} \gamma^{*}_{\mathcal J}:~H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} \omega_{\mathcal J} \otimes_{\mathbb Z} \mathbb C\end{align} $$
$$ \begin{align} \gamma^{*}_{\mathcal J}:~H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} \omega_{\mathcal J} \otimes_{\mathbb Z} \mathbb C\end{align} $$
calculated with respect to
![]() $H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
and the integral structure
$H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
and the integral structure
![]() $i_{\omega _{\mathcal J}}$
.
$i_{\omega _{\mathcal J}}$
.
(ii)
![]() $det_{\mathcal O_{F}}(\gamma _{\mathcal J}^{*})$
is the determinant of (37) with respect to
$det_{\mathcal O_{F}}(\gamma _{\mathcal J}^{*})$
is the determinant of (37) with respect to
![]() $H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
and the
$H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
and the
![]() $\mathcal O_{F}$
-integral structure
$\mathcal O_{F}$
-integral structure
![]() $j_{ \omega _{\mathcal J} }$
(Definition 8).
$j_{ \omega _{\mathcal J} }$
(Definition 8).
The main result of this section is the following.
Theorem 23. One has (up to a power of 2)
 $$ \begin{align*}det(\gamma_{\mathcal J}^{*})= \pm \frac{P_{J,\infty}}{|d_{F}|^{g/2}} = \pm ({\sqrt{-1}})^{g~\cdot~r_{2}}~\cdot~\frac{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) }{\sqrt{d_{F}}^{g}}.\end{align*} $$
$$ \begin{align*}det(\gamma_{\mathcal J}^{*})= \pm \frac{P_{J,\infty}}{|d_{F}|^{g/2}} = \pm ({\sqrt{-1}})^{g~\cdot~r_{2}}~\cdot~\frac{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) }{\sqrt{d_{F}}^{g}}.\end{align*} $$
Remark 24. (i) As we shall see below, the factor
![]() $\sqrt {d_{F}}^{g}$
arises from the change of integral structures and the factor
$\sqrt {d_{F}}^{g}$
arises from the change of integral structures and the factor
![]() $\mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta }) $
appears if
$\mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta }) $
appears if
![]() $\omega _{\mathcal J}$
is not free and if F is totally real; then
$\omega _{\mathcal J}$
is not free and if F is totally real; then
![]() $P_{J, \infty } = det_{\mathcal O_{F}}(\gamma ^{*}_{\mathcal J})$
up to a power of 2 (because (31) – but not (37) – uses
$P_{J, \infty } = det_{\mathcal O_{F}}(\gamma ^{*}_{\mathcal J})$
up to a power of 2 (because (31) – but not (37) – uses
![]() $\pi _{0}(A_{\sigma }(\mathbb R))$
, a finite 2-group). Finally, there is a factor of
$\pi _{0}(A_{\sigma }(\mathbb R))$
, a finite 2-group). Finally, there is a factor of
![]() $\sqrt {-1}^{r_{2}~\cdot ~g}$
because the definition of
$\sqrt {-1}^{r_{2}~\cdot ~g}$
because the definition of
![]() $P_{J,\infty }$
uses a different Betti lattice at complex places.
$P_{J,\infty }$
uses a different Betti lattice at complex places.
(ii) As
![]() $det(\gamma _{\mathcal J}^{*})$
uses only the underlying abelian group of
$det(\gamma _{\mathcal J}^{*})$
uses only the underlying abelian group of
![]() $\omega _{\mathcal J}$
, one observes that the actual
$\omega _{\mathcal J}$
, one observes that the actual
![]() $\mathcal O_{F}$
-structure on
$\mathcal O_{F}$
-structure on
![]() $\omega _{\mathcal J}$
is irrelevant for Conjecture 20. This observation has the following implication. As in Remark 19, let A be an abelian variety over F and let
$\omega _{\mathcal J}$
is irrelevant for Conjecture 20. This observation has the following implication. As in Remark 19, let A be an abelian variety over F and let
![]() $A^{\prime }$
be its restriction to
$A^{\prime }$
be its restriction to
![]() $F^{\prime }\subset F$
; let
$F^{\prime }\subset F$
; let
![]() $\mathcal N$
and
$\mathcal N$
and
![]() $\mathcal N^{\prime }$
be their Néron models. Conjecture 20 for an abelian variety A over F is equivalent to Conjecture 20 for
$\mathcal N^{\prime }$
be their Néron models. Conjecture 20 for an abelian variety A over F is equivalent to Conjecture 20 for
![]() $A^{\prime }$
over
$A^{\prime }$
over
![]() $F^{\prime }$
. A key step in the proof of the equivalence is showing that [Reference Conrad7, §6]
$F^{\prime }$
. A key step in the proof of the equivalence is showing that [Reference Conrad7, §6]
 $$ \begin{align*} \frac{P_{A,\infty}}{(|d_{F}|)^{g/2}} = \frac{P_{A^{\prime},\infty}}{(|d_{F^{\prime}} |)^{\frac{g[F:F^{\prime}]}{2}}}.\end{align*} $$
$$ \begin{align*} \frac{P_{A,\infty}}{(|d_{F}|)^{g/2}} = \frac{P_{A^{\prime},\infty}}{(|d_{F^{\prime}} |)^{\frac{g[F:F^{\prime}]}{2}}}.\end{align*} $$
This is clear from Theorem 23 as
![]() $\omega _{\mathcal N}$
is isomorphic to
$\omega _{\mathcal N}$
is isomorphic to
![]() $\omega _{\mathcal N^{\prime }}$
as abelian groups and the period isomorphism
$\omega _{\mathcal N^{\prime }}$
as abelian groups and the period isomorphism
![]() $\gamma _{\mathcal N}$
is the same as
$\gamma _{\mathcal N}$
is the same as
![]() $\gamma _{\mathcal N^{\prime }}$
.
$\gamma _{\mathcal N^{\prime }}$
.
Proof. (of Theorem 23) It is difficult to calculate or write down a formula directly for
![]() $det(\gamma _{\mathcal J}^{*})$
as the integral structure
$det(\gamma _{\mathcal J}^{*})$
as the integral structure
![]() $i_{\omega _{\mathcal J}}$
is not easy to describe explicitly. So one has to use
$i_{\omega _{\mathcal J}}$
is not easy to describe explicitly. So one has to use
![]() $j_{\omega _{\mathcal J}}$
. By Proposition 9, one has
$j_{\omega _{\mathcal J}}$
. By Proposition 9, one has
 $$ \begin{align*} det_{\mathcal O_{F}}(\gamma^{*}_{\mathcal J}) = det(\gamma^{*}_{\mathcal J})~\cdot~\sqrt{d_{F}}^{g}.\end{align*} $$
$$ \begin{align*} det_{\mathcal O_{F}}(\gamma^{*}_{\mathcal J}) = det(\gamma^{*}_{\mathcal J})~\cdot~\sqrt{d_{F}}^{g}.\end{align*} $$
We shall now see how to compute
![]() $det_{{\mathcal O}_{F}}(\gamma _{\mathcal J})$
explicitly in the style of Subsection 3.2.
$det_{{\mathcal O}_{F}}(\gamma _{\mathcal J})$
explicitly in the style of Subsection 3.2.
4.0.1 The case that
 $N= {\omega }_{ \mathcal J}$
is free
$N= {\omega }_{ \mathcal J}$
is free
If N is free as an
![]() ${\mathcal O}_{F}$
-module (its rank is g), then pick an
${\mathcal O}_{F}$
-module (its rank is g), then pick an
![]() ${\mathcal O}_{F}$
-basis
${\mathcal O}_{F}$
-basis
![]() $\mathcal B = \{v_{1}, \cdots , v_{g}\}$
for it. If
$\mathcal B = \{v_{1}, \cdots , v_{g}\}$
for it. If
![]() ${\mathcal B}^{\prime }$
is a different basis for N, then the determinant
${\mathcal B}^{\prime }$
is a different basis for N, then the determinant
![]() $d(\mathcal B, {\mathcal B}^{\prime })$
of the change of basis matrix is a unit in
$d(\mathcal B, {\mathcal B}^{\prime })$
of the change of basis matrix is a unit in
![]() ${\mathcal O}_{F}$
. Note that
${\mathcal O}_{F}$
. Note that
![]() $\mathcal B$
is also a basis for the F-vector space
$\mathcal B$
is also a basis for the F-vector space
![]() $\omega _{\mathcal J}\otimes _{{\mathcal O}_{F}}F = H^{0}(J, \Omega ^{1})$
. For any embedding
$\omega _{\mathcal J}\otimes _{{\mathcal O}_{F}}F = H^{0}(J, \Omega ^{1})$
. For any embedding
![]() $\sigma : F \to \mathbb C$
, let
$\sigma : F \to \mathbb C$
, let
be the image of
![]() $\mathcal B$
under the isomorphism (via
$\mathcal B$
under the isomorphism (via
![]() $\sigma $
)
$\sigma $
)
So
![]() $\sigma (\mathcal B)$
is a basis for the complex vector space
$\sigma (\mathcal B)$
is a basis for the complex vector space
![]() $H^{0}(J_{\sigma }(\mathbb C), \Omega ^{1})$
. Just as a basis for V and W produces a basis for
$H^{0}(J_{\sigma }(\mathbb C), \Omega ^{1})$
. Just as a basis for V and W produces a basis for
![]() $V \times W$
, we can combine the bases
$V \times W$
, we can combine the bases
![]() $\sigma (\mathcal B)$
for
$\sigma (\mathcal B)$
for
![]() $\sigma \in \tilde {S}$
to get a basis
$\sigma \in \tilde {S}$
to get a basis
![]() $\tilde {\mathcal B}$
for the complex vector space
$\tilde {\mathcal B}$
for the complex vector space
 $$ \begin{align*}H^{0}(J_{\mathbb C}, \Omega^{1}) = H^{0}(J, \Omega^{1})\otimes_{\mathbb Z} \mathbb C= \prod_{\sigma \in \tilde{S}} H^{0}(J_{\sigma}(\mathbb C), \Omega^{1}).\end{align*} $$
$$ \begin{align*}H^{0}(J_{\mathbb C}, \Omega^{1}) = H^{0}(J, \Omega^{1})\otimes_{\mathbb Z} \mathbb C= \prod_{\sigma \in \tilde{S}} H^{0}(J_{\sigma}(\mathbb C), \Omega^{1}).\end{align*} $$
The lattice (
![]() $\mathbb Z$
-module) spanned by
$\mathbb Z$
-module) spanned by
![]() $\tilde {\mathcal B}$
represents the
$\tilde {\mathcal B}$
represents the
![]() ${\mathcal O}_{F}$
-integral structure
${\mathcal O}_{F}$
-integral structure
![]() $j_{N}$
on
$j_{N}$
on
![]() $V =N\otimes _{\mathbb Z}\mathbb C$
(see Definition 8). The determinant
$V =N\otimes _{\mathbb Z}\mathbb C$
(see Definition 8). The determinant
![]() $D(\mathcal B)$
of (37) computed with respect to the integral structure provided by
$D(\mathcal B)$
of (37) computed with respect to the integral structure provided by
![]() $\tilde {\mathcal B}$
is equal to
$\tilde {\mathcal B}$
is equal to
![]() $det_{{\mathcal O}_{F}}(\gamma ^{*}_{\mathcal J})$
. Let us show that
$det_{{\mathcal O}_{F}}(\gamma ^{*}_{\mathcal J})$
. Let us show that
![]() $D(\mathcal B)$
is independent of the basis
$D(\mathcal B)$
is independent of the basis
![]() $\tilde {\mathcal B}$
.
$\tilde {\mathcal B}$
.
Given another basis
![]() ${\mathcal B}^{\prime }$
for N, we have
${\mathcal B}^{\prime }$
for N, we have
 $$ \begin{align*}D({\mathcal B}^{\prime}) = D(\mathcal B) \prod_{\sigma\in \tilde{S} }\sigma(d_{\mathcal B, {\mathcal B}^{\prime}}).\end{align*} $$
$$ \begin{align*}D({\mathcal B}^{\prime}) = D(\mathcal B) \prod_{\sigma\in \tilde{S} }\sigma(d_{\mathcal B, {\mathcal B}^{\prime}}).\end{align*} $$
The determinant of the change of basis matrix from
![]() $\tilde {\mathcal B}$
to
$\tilde {\mathcal B}$
to
![]() $\tilde {{\mathcal B}^{\prime }}$
is
$\tilde {{\mathcal B}^{\prime }}$
is
 $$ \begin{align*}\prod_{\sigma\in \tilde{S}}\sigma(d_{\mathcal B, {\mathcal B}^{\prime}}) = \mathbb N_{F/{\mathbb Q}}d_{\mathcal B, {\mathcal B}^{\prime}} =\pm 1\end{align*} $$
$$ \begin{align*}\prod_{\sigma\in \tilde{S}}\sigma(d_{\mathcal B, {\mathcal B}^{\prime}}) = \mathbb N_{F/{\mathbb Q}}d_{\mathcal B, {\mathcal B}^{\prime}} =\pm 1\end{align*} $$
as
![]() $d_{\mathcal B, {\mathcal B}^{\prime }}$
is a unit in
$d_{\mathcal B, {\mathcal B}^{\prime }}$
is a unit in
![]() ${\mathcal O}_{F}$
. Though the integral structure on
${\mathcal O}_{F}$
. Though the integral structure on
![]() $N\otimes _{\mathbb Z} \mathbb C$
provided by
$N\otimes _{\mathbb Z} \mathbb C$
provided by
![]() $\tilde {\mathcal B}$
depends on the choice of
$\tilde {\mathcal B}$
depends on the choice of
![]() $\mathcal B$
, the number
$\mathcal B$
, the number
![]() $D(\mathcal B)$
is independent of the basis
$D(\mathcal B)$
is independent of the basis
![]() $\mathcal {B}$
: Any two
$\mathcal {B}$
: Any two
![]() ${\mathcal O}_{F}$
-bases of N provide Euler-equivalent integral structures representing
${\mathcal O}_{F}$
-bases of N provide Euler-equivalent integral structures representing
![]() $j_{N}$
on
$j_{N}$
on
![]() $V=N\otimes _{\mathbb Z} \mathbb C$
. Thus, in this case, for any basis
$V=N\otimes _{\mathbb Z} \mathbb C$
. Thus, in this case, for any basis
![]() $\mathcal B$
, one has
$\mathcal B$
, one has
 $$ \begin{align*} det(\gamma^{*}_{\mathcal J}) = \frac{D(\mathcal B)}{{\sqrt{d_{F}}^{g}}}.\end{align*} $$
$$ \begin{align*} det(\gamma^{*}_{\mathcal J}) = \frac{D(\mathcal B)}{{\sqrt{d_{F}}^{g}}}.\end{align*} $$
4.0.2 The case that
 $N= \omega _{\mathcal J}$
is not free as a
$N= \omega _{\mathcal J}$
is not free as a
 ${\mathcal O}_{F}$
-module
${\mathcal O}_{F}$
-module
In this case, we proceed as in Subsection 3.2 using the top exterior power
![]() $\Lambda ^{g} N$
of the projective
$\Lambda ^{g} N$
of the projective
![]() ${\mathcal O}_{F}$
-module N. Let
${\mathcal O}_{F}$
-module N. Let
![]() $\mathcal B = \{v_{1}, \cdots , v_{g}\}$
be a F-basis of
$\mathcal B = \{v_{1}, \cdots , v_{g}\}$
be a F-basis of
![]() $H^{0}(J, \Omega ^{1})$
and put
$H^{0}(J, \Omega ^{1})$
and put
![]() $\rho = v_{1} \wedge \cdots \wedge v_{g}$
. We have
$\rho = v_{1} \wedge \cdots \wedge v_{g}$
. We have
 $$ \begin{align} \Lambda^{g} N = \mathfrak b_{\rho}~\cdot~ \rho \subset \Lambda^{g} H^{0}(J, \Omega^{1}) \end{align} $$
$$ \begin{align} \Lambda^{g} N = \mathfrak b_{\rho}~\cdot~ \rho \subset \Lambda^{g} H^{0}(J, \Omega^{1}) \end{align} $$
where
![]() $\mathfrak b_{\rho }$
is a fractional ideal of
$\mathfrak b_{\rho }$
is a fractional ideal of
![]() ${\mathcal O}_{F}$
. For any
${\mathcal O}_{F}$
. For any
![]() $k \neq 0 \in F$
, one has an equality of fractional ideals
$k \neq 0 \in F$
, one has an equality of fractional ideals
As before, let
![]() $\tilde {\mathcal B}$
denote the basis of
$\tilde {\mathcal B}$
denote the basis of
![]() $V=N\otimes _{\mathbb Z} \mathbb C$
obtained from
$V=N\otimes _{\mathbb Z} \mathbb C$
obtained from
![]() $\mathcal B$
. Let
$\mathcal B$
. Let
![]() $D(\mathcal B)$
denote the determinant of (37) with respect to the basis
$D(\mathcal B)$
denote the determinant of (37) with respect to the basis
![]() $\tilde {\mathcal B}$
and
$\tilde {\mathcal B}$
and
![]() $H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
. Using (38), one has
$H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
. Using (38), one has
Let us directly show that the right-hand side is independent of the basis. Given any basis
![]() ${\mathcal B}^{\prime }=\{v_{1}^{\prime },\cdots , v_{g}^{\prime }\}$
,
${\mathcal B}^{\prime }=\{v_{1}^{\prime },\cdots , v_{g}^{\prime }\}$
,
 $$ \begin{align*} D({\mathcal B}^{\prime}) = D(\mathcal B) \prod_{\sigma \in \tilde{S} } \sigma(k) \qquad k:= d(\mathcal B, {\mathcal B}^{\prime}).\end{align*} $$
$$ \begin{align*} D({\mathcal B}^{\prime}) = D(\mathcal B) \prod_{\sigma \in \tilde{S} } \sigma(k) \qquad k:= d(\mathcal B, {\mathcal B}^{\prime}).\end{align*} $$
Note that
![]() $k= d(\mathcal B, {\mathcal B}^{\prime })\in F^{\times }$
need not be a unit.
$k= d(\mathcal B, {\mathcal B}^{\prime })\in F^{\times }$
need not be a unit.
If
![]() $\rho ^{\prime }= v_{1}^{\prime }\wedge \cdots \wedge v_{g}^{\prime }$
, then
$\rho ^{\prime }= v_{1}^{\prime }\wedge \cdots \wedge v_{g}^{\prime }$
, then
which gives
 $$ \begin{align*}b_{\rho^{\prime}} = b_{\rho}~\cdot~(k)^{-1}.\end{align*} $$
$$ \begin{align*}b_{\rho^{\prime}} = b_{\rho}~\cdot~(k)^{-1}.\end{align*} $$
Thus, using (34) as in Lemma 17, we find
 $$ \begin{align*}D({\mathcal B}^{\prime}) &\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho^{\prime}} = D(\mathcal B)~\cdot~( \prod_{\sigma \in \tilde{S} } \sigma(k))~\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho^{\prime}} = D(\mathcal B) \nonumber \\ & \cdot~(\prod_{\sigma \in \tilde{S}} \sigma(k))~\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho}~\cdot~(\mathbb N_{F/{\mathbb Q}}(k))^{-1} = D(\mathcal B)~\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho}.\end{align*} $$
$$ \begin{align*}D({\mathcal B}^{\prime}) &\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho^{\prime}} = D(\mathcal B)~\cdot~( \prod_{\sigma \in \tilde{S} } \sigma(k))~\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho^{\prime}} = D(\mathcal B) \nonumber \\ & \cdot~(\prod_{\sigma \in \tilde{S}} \sigma(k))~\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho}~\cdot~(\mathbb N_{F/{\mathbb Q}}(k))^{-1} = D(\mathcal B)~\cdot~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho}.\end{align*} $$
Thus,
![]() $D(\mathcal B)~\cdot ~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho }$
is independent of
$D(\mathcal B)~\cdot ~\mathbb N_{F/{\mathbb Q}} \mathfrak b_{\rho }$
is independent of
![]() $\mathcal B$
.
$\mathcal B$
.
4.0.3 Betti lattices
It should be clear that the above computation of
![]() $det_{{\mathcal O}_{F}}(\gamma ^{*}_{\mathcal J})$
is exactly the computation of
$det_{{\mathcal O}_{F}}(\gamma ^{*}_{\mathcal J})$
is exactly the computation of
![]() $P_{J,\infty }$
in Subsection 3.2. In fact, for any g-dimensional abelian variety A over F, one has (up to a power of 2)
$P_{J,\infty }$
in Subsection 3.2. In fact, for any g-dimensional abelian variety A over F, one has (up to a power of 2)
Here, as in Subsection 3.2,
![]() $\mathcal N$
is the Néron model of A and
$\mathcal N$
is the Néron model of A and
![]() $\gamma ^{*}_{\mathcal N}$
is the period isomorphism
$\gamma ^{*}_{\mathcal N}$
is the period isomorphism
 $$ \begin{align*}\gamma^{*}_{\mathcal N}:~H^{1}_{B}(A_{\mathbb C}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} \omega_{\mathcal N} \otimes_{\mathbb Z} \mathbb C.\end{align*} $$
$$ \begin{align*}\gamma^{*}_{\mathcal N}:~H^{1}_{B}(A_{\mathbb C}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} \omega_{\mathcal N} \otimes_{\mathbb Z} \mathbb C.\end{align*} $$
Let
![]() $B= \{w_{1}, \cdots , w_{g}\}$
be an F-basis of
$B= \{w_{1}, \cdots , w_{g}\}$
be an F-basis of
![]() $H^{0}(A, \Omega ^{1})$
and put
$H^{0}(A, \Omega ^{1})$
and put
![]() $\eta = w_{1}\wedge \cdots \wedge w_{g}$
. The discrepancy in (40) arises from the fact that the Betti lattices are different.
$\eta = w_{1}\wedge \cdots \wedge w_{g}$
. The discrepancy in (40) arises from the fact that the Betti lattices are different.
For a real place of S corresponding to
![]() $\sigma : F \to \mathbb R$
, consider the period isomorphism
$\sigma : F \to \mathbb R$
, consider the period isomorphism
 $$ \begin{align*} \gamma_{\sigma}= H^{1}_{B}(A_{\sigma}(\mathbb C) , \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} H^{0}(A_{\sigma}, \Omega^{1}).\end{align*} $$
$$ \begin{align*} \gamma_{\sigma}= H^{1}_{B}(A_{\sigma}(\mathbb C) , \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} H^{0}(A_{\sigma}, \Omega^{1}).\end{align*} $$
For a complex place v of S (corresponding to
![]() $\sigma : F \to \mathbb C$
and its conjugate
$\sigma : F \to \mathbb C$
and its conjugate
![]() $c\sigma $
), consider the complex abelian variety
$c\sigma $
), consider the complex abelian variety
and the period isomorphism
 $$ \begin{align*}\gamma_{v}: H^{1}_{B}(A_{v}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} H^{0}(A_{v}, \Omega^{1}).\end{align*} $$
$$ \begin{align*}\gamma_{v}: H^{1}_{B}(A_{v}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} H^{0}(A_{v}, \Omega^{1}).\end{align*} $$
For real places, the groups in
![]() $\gamma _{\sigma }$
are the same as the one used in (31); in this case,
$\gamma _{\sigma }$
are the same as the one used in (31); in this case,
![]() $p_{\sigma }(A, \eta )$
is the determinantFootnote
2
of
$p_{\sigma }(A, \eta )$
is the determinantFootnote
2
of
![]() $\gamma _{\sigma }$
relative to the basis
$\gamma _{\sigma }$
relative to the basis
![]() $H^{1}_{B}(A_{\sigma }(\mathbb C) , \mathbb Z)^{+}$
and
$H^{1}_{B}(A_{\sigma }(\mathbb C) , \mathbb Z)^{+}$
and
![]() $B= \{w_{1}, \cdots , w_{g}\}$
.
$B= \{w_{1}, \cdots , w_{g}\}$
.
For complex places v, (32) uses
![]() $H^{1}(A_{\sigma }, \mathbb Z)$
instead of
$H^{1}(A_{\sigma }, \mathbb Z)$
instead of
![]() $H^{1}_{B}(A_{v}, \mathbb Z)^{+}$
. In this case,
$H^{1}_{B}(A_{v}, \mathbb Z)^{+}$
. In this case,
![]() $(\sqrt {-1})^{g}~\cdot ~p_{v}(A, \eta )$
is the determinant of
$(\sqrt {-1})^{g}~\cdot ~p_{v}(A, \eta )$
is the determinant of
![]() $\gamma _{v}$
relative to the basis
$\gamma _{v}$
relative to the basis
![]() $H^{1}_{B}(A_{v}, \mathbb Z)^{+}$
and B. This is what leads to the discrepancy between the two invariants. What follows is presumably well-known, but we include it for sake of completeness.
$H^{1}_{B}(A_{v}, \mathbb Z)^{+}$
and B. This is what leads to the discrepancy between the two invariants. What follows is presumably well-known, but we include it for sake of completeness.
Complex conjugation
simply permutes the factors of
![]() ${A}_{v}$
. One has the decomposition
${A}_{v}$
. One has the decomposition
 $$ \begin{align*}H_{1}({A_{v}}(\mathbb C), \mathbb Z) &= H_{1}(A_{\sigma}(\mathbb C), \mathbb Z) \oplus H_{1}(A_{c\sigma} (\mathbb C), \mathbb Z), \nonumber \\ H^{0}({A_{v}}, \Omega^{1}) &= H^{0}(A_{\sigma}, \Omega^{1}) \oplus H^{0}(A_{c\sigma}, \Omega^{1}).\end{align*} $$
$$ \begin{align*}H_{1}({A_{v}}(\mathbb C), \mathbb Z) &= H_{1}(A_{\sigma}(\mathbb C), \mathbb Z) \oplus H_{1}(A_{c\sigma} (\mathbb C), \mathbb Z), \nonumber \\ H^{0}({A_{v}}, \Omega^{1}) &= H^{0}(A_{\sigma}, \Omega^{1}) \oplus H^{0}(A_{c\sigma}, \Omega^{1}).\end{align*} $$
Concretely, a basis for
![]() $H_{1}({A_{v}}, \mathbb Z)$
is given by
$H_{1}({A_{v}}, \mathbb Z)$
is given by
a basis for
![]() $H^{0}(A_{v}, \Omega ^{1})$
is given by (here the image of
$H^{0}(A_{v}, \Omega ^{1})$
is given by (here the image of
![]() $w_{j}$
is denoted as
$w_{j}$
is denoted as
![]() $w_{j}$
on
$w_{j}$
on
![]() $A_{\sigma }$
and as
$A_{\sigma }$
and as
![]() $cw_{j}$
on
$cw_{j}$
on
![]() $A_{c\sigma }$
)
$A_{c\sigma }$
)
So a basis for
![]() $H_{1}(A_{v}, \mathbb Z)^{+}$
is given by
$H_{1}(A_{v}, \mathbb Z)^{+}$
is given by
For the complex place v and
![]() $\eta $
, the determinant of
$\eta $
, the determinant of
![]() $\gamma _{v}$
relative to the basis
$\gamma _{v}$
relative to the basis
![]() $H^{1}_{B}(A_{v}, \mathbb Z)^{+}$
and B is the determinant of the
$H^{1}_{B}(A_{v}, \mathbb Z)^{+}$
and B is the determinant of the
![]() $2g \times 2g$
-matrix M
$2g \times 2g$
-matrix M

Observe that (in a product
![]() $V \times W$
of manifolds, a differential form from W does not pair with a cycle from V)
$V \times W$
of manifolds, a differential form from W does not pair with a cycle from V)
 $$ \begin{align*}\int_{(\gamma_{i}, c\gamma_{i})} (w_{j}, 0) = \int_{\gamma_{i}} w_{j}, \qquad \int_{(\gamma_{i}, c\gamma_{i})} (0, cw_{j}) = \int_{c\gamma_{i}} c w_{j}.\end{align*} $$
$$ \begin{align*}\int_{(\gamma_{i}, c\gamma_{i})} (w_{j}, 0) = \int_{\gamma_{i}} w_{j}, \qquad \int_{(\gamma_{i}, c\gamma_{i})} (0, cw_{j}) = \int_{c\gamma_{i}} c w_{j}.\end{align*} $$
So the matrix M can be rewritten as
 $$ \begin{align*} M=\begin{bmatrix} \int_{\gamma_{1}} w_{1} & \int_{\gamma_{1}} w_{2} & \cdots & \int_{\gamma_{1}} w_{g} & \int_{c\gamma_{1}} cw_{1} & \cdots & \int_{ c\gamma_{1}} cw_{g}\\ \int_{\gamma_{2}} w_{1} & \int_{\gamma_{2}} w_{2} & \cdots & \int_{\gamma_{2}} w_{g} &\int_{c\gamma_{2}} cw_{1} & \cdots & \int_{c\gamma_{2}} cw_{g}\\ \cdots &\cdots & \cdots &\cdots &\cdots &\cdots & \cdots\\ \cdots &\cdots & \cdots &\cdots &\cdots &\cdots & \cdots\\ \cdots &\cdots & \cdots &\cdots &\cdots &\cdots & \cdots\\ \int_{\gamma_{2g}} w_{1} & \int_{\gamma_{2g}} w_{2} & \cdots & \int_{\gamma_{2g}} w_{g} & \int_{ c\gamma_{2g} } cw_{1} & \cdots & \int_{ c\gamma_{2g}} cw_{g} \end{bmatrix}. \end{align*} $$
$$ \begin{align*} M=\begin{bmatrix} \int_{\gamma_{1}} w_{1} & \int_{\gamma_{1}} w_{2} & \cdots & \int_{\gamma_{1}} w_{g} & \int_{c\gamma_{1}} cw_{1} & \cdots & \int_{ c\gamma_{1}} cw_{g}\\ \int_{\gamma_{2}} w_{1} & \int_{\gamma_{2}} w_{2} & \cdots & \int_{\gamma_{2}} w_{g} &\int_{c\gamma_{2}} cw_{1} & \cdots & \int_{c\gamma_{2}} cw_{g}\\ \cdots &\cdots & \cdots &\cdots &\cdots &\cdots & \cdots\\ \cdots &\cdots & \cdots &\cdots &\cdots &\cdots & \cdots\\ \cdots &\cdots & \cdots &\cdots &\cdots &\cdots & \cdots\\ \int_{\gamma_{2g}} w_{1} & \int_{\gamma_{2g}} w_{2} & \cdots & \int_{\gamma_{2g}} w_{g} & \int_{ c\gamma_{2g} } cw_{1} & \cdots & \int_{ c\gamma_{2g}} cw_{g} \end{bmatrix}. \end{align*} $$
As
![]() $A_{\sigma }$
and
$A_{\sigma }$
and
![]() $A_{c\sigma }$
are complex conjugate abelian varieties, one has
$A_{c\sigma }$
are complex conjugate abelian varieties, one has
 $$ \begin{align*}\int_{ c\gamma_{i} } cw_{j} = \overline{\int_{\gamma_{i} } w_{j}};\end{align*} $$
$$ \begin{align*}\int_{ c\gamma_{i} } cw_{j} = \overline{\int_{\gamma_{i} } w_{j}};\end{align*} $$
it follows that M and
![]() $M_{v}(A, \eta )$
of (32) satisfy
$M_{v}(A, \eta )$
of (32) satisfy
Remark 16 shows that
 $$ \begin{align*}\prod_{v\in S_{\infty}} \textrm{det}(M_{v} (A, \eta))\end{align*} $$
$$ \begin{align*}\prod_{v\in S_{\infty}} \textrm{det}(M_{v} (A, \eta))\end{align*} $$
is a real number multiplied by
![]() $({\sqrt {-1}})^{g~\cdot ~r_{2}}$
. This proves the identity (40); combining it with Proposition 9 provides (up to a power of 2)
$({\sqrt {-1}})^{g~\cdot ~r_{2}}$
. This proves the identity (40); combining it with Proposition 9 provides (up to a power of 2)
 $$ \begin{align*} det(\gamma^{*}_{\mathcal J}) = \frac{ det_{{\mathcal O}_{F}}(\gamma^{*}_{\mathcal J})}{\sqrt{d_{F}}^{g}} = \pm ({\sqrt{-1}})^{g~\cdot~r_{2}} \frac{P_{J,\infty}}{\sqrt{d_{F}}^{g}}.\end{align*} $$
$$ \begin{align*} det(\gamma^{*}_{\mathcal J}) = \frac{ det_{{\mathcal O}_{F}}(\gamma^{*}_{\mathcal J})}{\sqrt{d_{F}}^{g}} = \pm ({\sqrt{-1}})^{g~\cdot~r_{2}} \frac{P_{J,\infty}}{\sqrt{d_{F}}^{g}}.\end{align*} $$
Theorem 23 follows using the well-known result that the sign of
![]() $d_{F}$
is
$d_{F}$
is
![]() $(-1)^{r_{2}}$
.
$(-1)^{r_{2}}$
.
Proposition 25. (i)
![]() $det_{{\mathcal O}_{F}}(\gamma _{\mathcal J}^{*}) $
is equal to the determinant
$det_{{\mathcal O}_{F}}(\gamma _{\mathcal J}^{*}) $
is equal to the determinant
![]() $det_{{\mathcal O}_{F}}(\gamma _{\mathcal J})$
of
$det_{{\mathcal O}_{F}}(\gamma _{\mathcal J})$
of
 $$ \begin{align*}\gamma_{\mathcal J}:~H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} \textrm{Lie}~(\mathcal J) \otimes_{\mathbb Z} \mathbb C\end{align*} $$
$$ \begin{align*}\gamma_{\mathcal J}:~H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} \textrm{Lie}~(\mathcal J) \otimes_{\mathbb Z} \mathbb C\end{align*} $$
calculated using the
![]() ${\mathcal O}_{F}$
-integral structure
${\mathcal O}_{F}$
-integral structure
![]() $j_{\textrm {Lie}~(\mathcal J)}$
(Definition 8) and the lattice
$j_{\textrm {Lie}~(\mathcal J)}$
(Definition 8) and the lattice
![]() $H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}$
.
$H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}$
.
(ii)
![]() $det(\gamma _{\mathcal J}^{*})= det(\gamma _{\mathcal J})$
.
$det(\gamma _{\mathcal J}^{*})= det(\gamma _{\mathcal J})$
.
Proof. (i) For any complex abelian variety A, the dual abelian variety
![]() $A^{t}$
satisfies
$A^{t}$
satisfies
 $$ \begin{align*} H_{1}(A^{t}, \mathbb Z) = H^{1}_{B}(A, \mathbb Z(1))& & \textrm{Lie}~A = H^{1}(A^{t}, \mathcal O) \\ \textrm{Hom}(H^{1}_{B}(A^{t}, \mathbb Z), \mathbb Z) = H^{1}_{B}(A, \mathbb Z(1)) && \textrm{Hom}_{\mathbb C}(H^{1}(A, \mathcal O), \mathbb C) = H^{0}(A^{t}, \Omega^{1}). \end{align*} $$
$$ \begin{align*} H_{1}(A^{t}, \mathbb Z) = H^{1}_{B}(A, \mathbb Z(1))& & \textrm{Lie}~A = H^{1}(A^{t}, \mathcal O) \\ \textrm{Hom}(H^{1}_{B}(A^{t}, \mathbb Z), \mathbb Z) = H^{1}_{B}(A, \mathbb Z(1)) && \textrm{Hom}_{\mathbb C}(H^{1}(A, \mathcal O), \mathbb C) = H^{0}(A^{t}, \Omega^{1}). \end{align*} $$
This shows that the period isomorphism
 $$ \begin{align*}\gamma_{A}: H^{1}_{B}(A, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}(A, \mathcal O)\end{align*} $$
$$ \begin{align*}\gamma_{A}: H^{1}_{B}(A, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}(A, \mathcal O)\end{align*} $$
is dual to the map
 $$ \begin{align*}\gamma^{*}_{A^{t}}: H^{1}_{B}(A^{t}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} H^{0}(A^{t}, \Omega^{1}).\end{align*} $$
$$ \begin{align*}\gamma^{*}_{A^{t}}: H^{1}_{B}(A^{t}, \mathbb Z)^{+}_{\mathbb C} \xleftarrow{\sim} H^{0}(A^{t}, \Omega^{1}).\end{align*} $$
Applying these to the self-dual Jacobian
![]() $J_{\mathbb C}$
gives that the lattice
$J_{\mathbb C}$
gives that the lattice
![]() $H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}$
is dual to the lattice
$H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}$
is dual to the lattice
![]() $H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
. The natural duality of the projective
$H^{1}_{B}(J_{\mathbb C}, \mathbb Z)^{+}$
. The natural duality of the projective
![]() ${\mathcal O}_{F}$
-modules
${\mathcal O}_{F}$
-modules
![]() $\textrm {Lie}~(\mathcal J)$
and
$\textrm {Lie}~(\mathcal J)$
and
![]() $\omega _{\mathcal J}$
shows, using Proposition 9, that the
$\omega _{\mathcal J}$
shows, using Proposition 9, that the
![]() ${\mathcal O}_{F}$
-integral structures
${\mathcal O}_{F}$
-integral structures
![]() $j_{\textrm {Lie}~(\mathcal J)}$
and
$j_{\textrm {Lie}~(\mathcal J)}$
and
![]() $j_{ \omega _{\mathcal J} }$
are dual. As the determinants of dual maps computed with respect to dual lattices are equal, the result follows.
$j_{ \omega _{\mathcal J} }$
are dual. As the determinants of dual maps computed with respect to dual lattices are equal, the result follows.
(ii) Proposition 9 and (i) imply
 $det(\gamma _{\mathcal J}^{*})~\cdot ~(\sqrt {d_{F}})^{g} = det_{{\mathcal O}_{F}}(\gamma _{\mathcal J}^{*}) =det_{{\mathcal O}_{F}}(\gamma _{\mathcal J}) =det(\gamma _{\mathcal J}) ~\cdot ~(\sqrt {d_{F}})^{g}$
.
$det(\gamma _{\mathcal J}^{*})~\cdot ~(\sqrt {d_{F}})^{g} = det_{{\mathcal O}_{F}}(\gamma _{\mathcal J}^{*}) =det_{{\mathcal O}_{F}}(\gamma _{\mathcal J}) =det(\gamma _{\mathcal J}) ~\cdot ~(\sqrt {d_{F}})^{g}$
.
5 Proof of Theorem 2 in a special case
Throughout this section, we assume that
![]() $\pi :X \to S$
is smooth and
$\pi :X \to S$
is smooth and
![]() $X_{0}(F)$
is nonempty. We prove Theorem 2 in this case by computing
$X_{0}(F)$
is nonempty. We prove Theorem 2 in this case by computing
![]() $H^{*}_{W}(X, \mathbb Z(1))$
and then use it to compare
$H^{*}_{W}(X, \mathbb Z(1))$
and then use it to compare
![]() $\chi (X,1)$
with Conjecture 21 for the Jacobian J of
$\chi (X,1)$
with Conjecture 21 for the Jacobian J of
![]() $X_{0}$
.
$X_{0}$
.
5.1 The groups
 $H^{*}_{W}(X, \mathbb Z(1))$
$H^{*}_{W}(X, \mathbb Z(1))$
By Subsection 2.8.1, we need to understand
![]() $\textrm {Pic}(X)$
and
$\textrm {Pic}(X)$
and
![]() $\textrm {Br}(X)$
.
$\textrm {Br}(X)$
.
Any
![]() $x\in X_{0}(F)$
provides
$x\in X_{0}(F)$
provides
![]() $ \text {Pic}(X_{0}) = J(F) \times \mathbb Z$
.
$ \text {Pic}(X_{0}) = J(F) \times \mathbb Z$
.
Proposition 26. One has (neglecting 2-torsion)

Proof. As
![]() $\pi :X\to S$
is smooth proper, any
$\pi :X\to S$
is smooth proper, any
![]() $x\in X_{0}(F)$
provides a splitting of the map
$x\in X_{0}(F)$
provides a splitting of the map
![]() $\textrm {Pic}(S) \to \textrm {Pic}(X)$
. The identity component
$\textrm {Pic}(S) \to \textrm {Pic}(X)$
. The identity component
 $\textrm {Pic}^{0}_{X/S}$
of the relative Picard scheme
$\textrm {Pic}^{0}_{X/S}$
of the relative Picard scheme
![]() $\textrm {Pic}_{X/S}$
is the Néron model
$\textrm {Pic}_{X/S}$
is the Néron model
![]() $\mathcal J$
of J by [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 1, page 264] and
$\mathcal J$
of J by [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 1, page 264] and
 $\textrm {Pic}_{X/S}(S) = \textrm {Pic}^{0}_{X/S}(S) \times \mathbb Z$
by [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 1, page 252]. As
$\textrm {Pic}_{X/S}(S) = \textrm {Pic}^{0}_{X/S}(S) \times \mathbb Z$
by [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 1, page 252]. As
![]() $\pi _{*}{\mathcal O}_{X} ={\mathcal O}_{S}$
, [Reference Bosch, Lütkebohmert and Raynaud4, Proposition 4, page 204] says
$\pi _{*}{\mathcal O}_{X} ={\mathcal O}_{S}$
, [Reference Bosch, Lütkebohmert and Raynaud4, Proposition 4, page 204] says
![]() $\textrm {Pic}_{X/S}(S) = \text {Pic}(X)/{\text {Pic}(S)}$
and
$\textrm {Pic}_{X/S}(S) = \text {Pic}(X)/{\text {Pic}(S)}$
and
![]() $\textrm {Pic}_{X/S}(F) = \text {Pic}(X_{0})$
. This proves (i). For (ii), we note that [Reference Tate36, Theorem 3.1] provides an exact (modulo 2-torsion) sequence
$\textrm {Pic}_{X/S}(F) = \text {Pic}(X_{0})$
. This proves (i). For (ii), we note that [Reference Tate36, Theorem 3.1] provides an exact (modulo 2-torsion) sequence
by class field theory,
![]() $\textrm {Br}(S)$
is a finite
$\textrm {Br}(S)$
is a finite
![]() $2$
-group.
$2$
-group.
5.2 The Euler characteristic
 $\chi _{B}(X,1)$
$\chi _{B}(X,1)$
We now compute the Euler characteristic of (21),
 $$ \begin{align*}\chi_{B}(X,1) = \frac{\chi(B(0,1)) \chi(B(2,1))}{\chi(B(1,1))}.\end{align*} $$
$$ \begin{align*}\chi_{B}(X,1) = \frac{\chi(B(0,1)) \chi(B(2,1))}{\chi(B(1,1))}.\end{align*} $$
Remark 27. As
![]() $\pi :X\to S$
is smooth,
$\pi :X\to S$
is smooth,
![]() $H^{1}(X_{s}, {\mathcal O}_{X_{s}})$
has dimension g over the residue field
$H^{1}(X_{s}, {\mathcal O}_{X_{s}})$
has dimension g over the residue field
![]() $k(s)$
for all points
$k(s)$
for all points
![]() $s\in S$
. Since S is a reduced noetherian scheme,
$s\in S$
. Since S is a reduced noetherian scheme,
![]() $\pi : X\to S$
is proper and
$\pi : X\to S$
is proper and
![]() ${\mathcal O}_{X}$
is a coherent sheaf on X flat over S, a result of Grothendieck (see L. Illusie’s article [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli9, Corollary 8.3.4]) states that
${\mathcal O}_{X}$
is a coherent sheaf on X flat over S, a result of Grothendieck (see L. Illusie’s article [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli9, Corollary 8.3.4]) states that
![]() $R^{1}\pi _{*}{\mathcal O}_{X} $
is locally free and that
$R^{1}\pi _{*}{\mathcal O}_{X} $
is locally free and that
![]() $R^{1}\pi _{*}{\mathcal O}_{X}\otimes k(s) \cong H^{1}(X_{s}, {\mathcal O}_{X_{s}})$
. So the
$R^{1}\pi _{*}{\mathcal O}_{X}\otimes k(s) \cong H^{1}(X_{s}, {\mathcal O}_{X_{s}})$
. So the
![]() ${\mathcal O}_{F}$
-module
${\mathcal O}_{F}$
-module
![]() $H^{1}(X, \mathcal O)$
is projective of rank g.
$H^{1}(X, \mathcal O)$
is projective of rank g.
5.2.1 The Euler characteristic of
 $B(1,1)$
$B(1,1)$
We write
![]() $det(\gamma _{X})$
for the determinant of
$det(\gamma _{X})$
for the determinant of
 $$ \begin{align} \gamma_{X}: H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C \end{align} $$
$$ \begin{align} \gamma_{X}: H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C \end{align} $$
with respect to the lattices
![]() $H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}$
and the abelian group underlying
$H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}$
and the abelian group underlying
![]() $H^{1}(X, \mathcal O)$
.
$H^{1}(X, \mathcal O)$
.
Lemma 28. The projective
![]() ${\mathcal O}_{F}$
-modules
${\mathcal O}_{F}$
-modules
![]() $H^{1}(\mathcal J, \mathcal O)$
and
$H^{1}(\mathcal J, \mathcal O)$
and
![]() $\omega _{\mathcal J}$
are dual.
$\omega _{\mathcal J}$
are dual.
Proof. As
![]() $\mathcal J \to S$
is an abelian scheme, its relative Picard scheme
$\mathcal J \to S$
is an abelian scheme, its relative Picard scheme
![]() $\textrm {Pic}_{\mathcal J/S}$
exists [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 5, p. 234] and its identity component
$\textrm {Pic}_{\mathcal J/S}$
exists [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 5, p. 234] and its identity component
 $\textrm {Pic}^{0}_{\mathcal J/S}$
is the dual abelian scheme
$\textrm {Pic}^{0}_{\mathcal J/S}$
is the dual abelian scheme
![]() $\mathcal J^{t} \to S$
. The S-points
$\mathcal J^{t} \to S$
. The S-points
![]() $\textrm {Lie}~\textrm {Pic}_{\mathcal J}$
of its Lie algebraFootnote
3
$\textrm {Lie}~\textrm {Pic}_{\mathcal J}$
of its Lie algebraFootnote
3
![]() ${Lie}~\textrm {Pic}_{\mathcal J}$
satisfy [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 1, p. 231], [Reference Liu, Lorenzini and Raynaud30, Proposition 1.1 (d)]
${Lie}~\textrm {Pic}_{\mathcal J}$
satisfy [Reference Bosch, Lütkebohmert and Raynaud4, Theorem 1, p. 231], [Reference Liu, Lorenzini and Raynaud30, Proposition 1.1 (d)]
 $$ \begin{align} \textrm{Lie}~(\mathcal J^{t})= \textrm{Lie~(Pic}_{\mathcal J/S}) \xrightarrow{\sim} H^{1}(\mathcal J, \mathcal O). \end{align} $$
$$ \begin{align} \textrm{Lie}~(\mathcal J^{t})= \textrm{Lie~(Pic}_{\mathcal J/S}) \xrightarrow{\sim} H^{1}(\mathcal J, \mathcal O). \end{align} $$
Since
![]() $J^{t}$
is the generic fibre of
$J^{t}$
is the generic fibre of
![]() $\mathcal J^{t}$
, the self-duality
$\mathcal J^{t}$
, the self-duality
![]() $J \cong J^{t}$
shows
$J \cong J^{t}$
shows
![]() $\mathcal J \cong \mathcal J^{t}$
and
$\mathcal J \cong \mathcal J^{t}$
and
![]() $\textrm {Lie}~(\mathcal J^{t}) \cong \textrm {Lie}~(\mathcal J)$
. Combining this with the natural duality between
$\textrm {Lie}~(\mathcal J^{t}) \cong \textrm {Lie}~(\mathcal J)$
. Combining this with the natural duality between
![]() $ \textrm {Lie}~(\mathcal J)$
and
$ \textrm {Lie}~(\mathcal J)$
and
![]() $\omega _{\mathcal J}$
[Reference Liu, Lorenzini and Raynaud30, Proposition 1.1 (c)] proves the lemma.
$\omega _{\mathcal J}$
[Reference Liu, Lorenzini and Raynaud30, Proposition 1.1 (c)] proves the lemma.
Proposition 29. One has
 $$ \begin{align*}\chi(B(1,1)) = \frac{P_{J, fin}}{P_{J}}= \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}.\end{align*} $$
$$ \begin{align*}\chi(B(1,1)) = \frac{P_{J, fin}}{P_{J}}= \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}.\end{align*} $$
Proof. Any
![]() $x\in X_{0}(F)$
gives a map
$x\in X_{0}(F)$
gives a map
the induced map
![]() $\beta $
on cohomology is independent of the choice of x; for example, it provides the following isomorphism:
$\beta $
on cohomology is independent of the choice of x; for example, it provides the following isomorphism:
of
![]() ${\mathcal O}_{F}$
-modules, which fits into a commutative diagram (using Lemma 28)
${\mathcal O}_{F}$
-modules, which fits into a commutative diagram (using Lemma 28)

as the vertical maps
![]() $\beta $
are isomorphisms, the integral structure corresponding to the map
$\beta $
are isomorphisms, the integral structure corresponding to the map
![]() $\gamma _{\mathcal J}$
(top row) is isomorphic to the one corresponding to
$\gamma _{\mathcal J}$
(top row) is isomorphic to the one corresponding to
![]() $\gamma _{X}$
(bottom row). As they are torsion-free, Theorem 23 and Proposition 25 show that
$\gamma _{X}$
(bottom row). As they are torsion-free, Theorem 23 and Proposition 25 show that
 $$ \begin{align*}\chi(\gamma_{X}) = \chi(\gamma_{\mathcal J}) = det(\gamma_{\mathcal J}) = \frac{P_{J, \infty}}{|d_{F}|^{g/2}}.\end{align*} $$
$$ \begin{align*}\chi(\gamma_{X}) = \chi(\gamma_{\mathcal J}) = det(\gamma_{\mathcal J}) = \frac{P_{J, \infty}}{|d_{F}|^{g/2}}.\end{align*} $$
Our convention for
![]() $B(1,1)$
is that
$B(1,1)$
is that
![]() $\textrm {Ker}(\gamma _{M})$
is in even degree, say, degree 0. We have
$\textrm {Ker}(\gamma _{M})$
is in even degree, say, degree 0. We have
 $$ \begin{align*} &B(1,1):~\underset{\textrm{degree 1}}{H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}} \to \underset{\textrm{degree 2}}{H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C}, \nonumber \\[3pt] & det (B(1,1)) = \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})} = \chi(B(1,1)). \\[-38pt] \end{align*} $$
$$ \begin{align*} &B(1,1):~\underset{\textrm{degree 1}}{H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}} \to \underset{\textrm{degree 2}}{H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C}, \nonumber \\[3pt] & det (B(1,1)) = \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})} = \chi(B(1,1)). \\[-38pt] \end{align*} $$
Combining Proposition 29 with (24) and (25) yields the following.
Proposition 30. We have
 $$ \begin{align*}\frac{1}{\chi_{B}(X,1)} = \frac{\chi(B(1,1))}{\chi(B(0,1)) \chi(B(2,1))} =\frac{(2\pi i)^{r_{2}}}{\sqrt{d_{F}}}~\cdot~ \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})} .\end{align*} $$
$$ \begin{align*}\frac{1}{\chi_{B}(X,1)} = \frac{\chi(B(1,1))}{\chi(B(0,1)) \chi(B(2,1))} =\frac{(2\pi i)^{r_{2}}}{\sqrt{d_{F}}}~\cdot~ \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})} .\end{align*} $$
5.3 The determinant of the sequence
 $C(1)$
$C(1)$
Using (16), (17), (18) and Proposition 26, the torsion in (22) satisfies
 $$ \begin{align*}\chi(C(1)_{tor}) = \frac{w~\cdot~[Br(X)]}{[\textrm{Pic}(X)_{tor}]^{2} } = \frac{w~\cdot~[Br(X)]} {h~\cdot~[J(F)_{tor}]~\cdot~h~\cdot~[J(F)_{tor}]}.\end{align*} $$
$$ \begin{align*}\chi(C(1)_{tor}) = \frac{w~\cdot~[Br(X)]}{[\textrm{Pic}(X)_{tor}]^{2} } = \frac{w~\cdot~[Br(X)]} {h~\cdot~[J(F)_{tor}]~\cdot~h~\cdot~[J(F)_{tor}]}.\end{align*} $$
As
![]() $\textrm {Hom}(\textrm {Pic}(X), \mathbb Z)\otimes \mathbb C \cong \mathbb C \times \textrm {Hom}(J(F), \mathbb Z)\otimes \mathbb C$
by Proposition 26, the sequence
$\textrm {Hom}(\textrm {Pic}(X), \mathbb Z)\otimes \mathbb C \cong \mathbb C \times \textrm {Hom}(J(F), \mathbb Z)\otimes \mathbb C$
by Proposition 26, the sequence
![]() $C(1)_{\mathbb C}$
of (22)
$C(1)_{\mathbb C}$
of (22)
 $$ \begin{align} 0 &\to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \underset{degree~2}{\textrm{Hom}(\textrm{Pic}(X), \mathbb C)} \xrightarrow{h} \underset{degree~3}{{\textrm{Pic}(X)}\otimes\mathbb C} \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \nonumber \\[3pt] &\to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb C)} \to 0. \end{align} $$
$$ \begin{align} 0 &\to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \underset{degree~2}{\textrm{Hom}(\textrm{Pic}(X), \mathbb C)} \xrightarrow{h} \underset{degree~3}{{\textrm{Pic}(X)}\otimes\mathbb C} \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \nonumber \\[3pt] &\to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb C)} \to 0. \end{align} $$
breaks up into exact sequences
 $$ \begin{align*} 0 \to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \mathbb C \to 0,\\ \underset{degree~2}{\textrm{Hom}(\textrm{Pic}^{0}(X), \mathbb C)} \xrightarrow{h} \underset{degree~3}{{\textrm{Pic}^{0}(X)}\otimes\mathbb C},\\ 0 \to \mathbb C \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb Z)\otimes\mathbb C} \to 0. \end{align*} $$
$$ \begin{align*} 0 \to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \mathbb C \to 0,\\ \underset{degree~2}{\textrm{Hom}(\textrm{Pic}^{0}(X), \mathbb C)} \xrightarrow{h} \underset{degree~3}{{\textrm{Pic}^{0}(X)}\otimes\mathbb C},\\ 0 \to \mathbb C \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb Z)\otimes\mathbb C} \to 0. \end{align*} $$
We compute
![]() $det(C(1))$
in three steps:
$det(C(1))$
in three steps:
-
• By (23), the first sequence is (14) and so has determinant R.
-
• By [Reference Lichtenbaum27, Conjecture 2.3.7] or (11), the map h is the Arakelov intersection pairing
By Faltings–Hriljac [Reference Faltings8, Reference Hriljac21], $$ \begin{align*}\textrm{Hom}(J(F), \mathbb Z)\otimes{\mathbb C} \to J(F)\otimes{\mathbb C}. \end{align*} $$
$$ \begin{align*}\textrm{Hom}(J(F), \mathbb Z)\otimes{\mathbb C} \to J(F)\otimes{\mathbb C}. \end{align*} $$
 $-h$
is the Néron–Tate height pairing (35) and so
$-h$
is the Néron–Tate height pairing (35) and so
 $det(h) = \pm \Theta _{NT}(J)$
.
$det(h) = \pm \Theta _{NT}(J)$
.
-
• As
 $t_{M_{2}} = H^{2}(X_{0}, \mathcal O) =0$
, one has
$t_{M_{2}} = H^{2}(X_{0}, \mathcal O) =0$
, one has
 $\textrm {Ker}(\gamma _{M_{2}}) = H^{2}(X_{\mathbb C}, \mathbb C(1))^{+} \cong \mathbb C^{r_{1}+r_{2}}$
. Using (18), the third sequence is (12) and so has determinant R.
$\textrm {Ker}(\gamma _{M_{2}}) = H^{2}(X_{\mathbb C}, \mathbb C(1))^{+} \cong \mathbb C^{r_{1}+r_{2}}$
. Using (18), the third sequence is (12) and so has determinant R.
Proposition 31. We have
 $$ \begin{align*} det(C(1)) = \frac{R \times R}{\Theta_{NT}} \qquad \chi (C(1)) = \frac{det(C(1))}{\chi(C(1)_{tor})}= \frac{h \times h [J(F)_{tor}] [J(F)_{tor}]}{[Br(X)] w } \frac{R \times R}{\Theta_{NT}} .\end{align*} $$
$$ \begin{align*} det(C(1)) = \frac{R \times R}{\Theta_{NT}} \qquad \chi (C(1)) = \frac{det(C(1))}{\chi(C(1)_{tor})}= \frac{h \times h [J(F)_{tor}] [J(F)_{tor}]}{[Br(X)] w } \frac{R \times R}{\Theta_{NT}} .\end{align*} $$
5.4 Completion of the proof of the main theorem in a special case
In this case, J has good reduction everywhere as
 $\textrm {Pic}^{0}_{X/S}$
is the Néron model of J; the group scheme
$\textrm {Pic}^{0}_{X/S}$
is the Néron model of J; the group scheme
![]() $\Phi _{v}$
is trivial and the Tamagawa numbers
$\Phi _{v}$
is trivial and the Tamagawa numbers
![]() $c_{v} =1$
for all v and
$c_{v} =1$
for all v and
![]() $P_{J,fin} =1$
. Conjecture 20 for
$P_{J,fin} =1$
. Conjecture 20 for
![]() $L(J,s)$
becomes Conjecture 21:
$L(J,s)$
becomes Conjecture 21:

We recall that
 $$ \begin{align*} \zeta(X,s) = \prod_{v\in S}\zeta(X_{v}, s), \qquad \zeta(X_{v}, s) = \frac{P_{1}(X_{v},s)}{P_{0}(X_{v}, s) P_{2}(X_{v}, s)}. \end{align*} $$
$$ \begin{align*} \zeta(X,s) = \prod_{v\in S}\zeta(X_{v}, s), \qquad \zeta(X_{v}, s) = \frac{P_{1}(X_{v},s)}{P_{0}(X_{v}, s) P_{2}(X_{v}, s)}. \end{align*} $$
As
![]() $\pi :X \to S$
is smooth and proper, one has
$\pi :X \to S$
is smooth and proper, one has
and
 $$ \begin{align} \prod_{v\in S}\frac{1}{P_{0}(X_{v},s)} = \zeta(S,s), \qquad \prod_{v\in S}\frac{1}{P_{2}(X_{v},s)} = \zeta(S,s-1), \quad L(J, s) = \prod_{v\in S} \frac{1}{P_{1}(X_{v},s)}.\end{align} $$
$$ \begin{align} \prod_{v\in S}\frac{1}{P_{0}(X_{v},s)} = \zeta(S,s), \qquad \prod_{v\in S}\frac{1}{P_{2}(X_{v},s)} = \zeta(S,s-1), \quad L(J, s) = \prod_{v\in S} \frac{1}{P_{1}(X_{v},s)}.\end{align} $$
Using (13), (15), we see that Conjecture 21 for
![]() $J/F$
is equivalent to the equality
$J/F$
is equivalent to the equality

Conjecture 1 for
![]() $\zeta ^{*}(X,1)$
says
$\zeta ^{*}(X,1)$
says
 $$ \begin{align*} \zeta^{*}(X,1) = \chi(X,1) = \frac{\chi_{A,C}(X,1)}{ \chi_{B}(X,1)} = \frac{{\chi(C(1))}}{\chi_{B}(X,1)~\cdot~ \chi(A^{\prime}(3,1))}.\end{align*} $$
$$ \begin{align*} \zeta^{*}(X,1) = \chi(X,1) = \frac{\chi_{A,C}(X,1)}{ \chi_{B}(X,1)} = \frac{{\chi(C(1))}}{\chi_{B}(X,1)~\cdot~ \chi(A^{\prime}(3,1))}.\end{align*} $$
 $$ \begin{align*}\chi(X,1) = {\frac{1}{w}}~\cdot~{\frac{[\textrm{Pic}(X)_{tor}]^{2}}{w ~[\textrm{Br}(X)]}~\frac{R \times R}{\Theta_{NT}}}~\cdot~ {\frac{(2\pi i )^{r_{2}}}{\sqrt{d_{F}}} \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) }}. \end{align*} $$
$$ \begin{align*}\chi(X,1) = {\frac{1}{w}}~\cdot~{\frac{[\textrm{Pic}(X)_{tor}]^{2}}{w ~[\textrm{Br}(X)]}~\frac{R \times R}{\Theta_{NT}}}~\cdot~ {\frac{(2\pi i )^{r_{2}}}{\sqrt{d_{F}}} \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta}) }}. \end{align*} $$
Proposition 26 shows that Conjecture 1 is equivalent to Conjecture 21 for J over F, up to powers of 2. This proves Theorem 2 in the special case
![]() $\pi :X\to S$
is smooth and
$\pi :X\to S$
is smooth and
![]() $X_{0}(F)$
is nonempty.
$X_{0}(F)$
is nonempty.
6 Towards the main theorem in the general case: arbitrary reduction
The assumption
![]() $\pi :X \to S$
is smooth and
$\pi :X \to S$
is smooth and
![]() $X_{0}(F)$
is nonempty leads to several simplifications such as
$X_{0}(F)$
is nonempty leads to several simplifications such as
![]() $H^{1}(X, \mathcal O)$
is torsion-free,
$H^{1}(X, \mathcal O)$
is torsion-free,
![]() , the intersection pairing on
, the intersection pairing on
![]() $\textrm {Pic}^{0}(X)$
is the Néron–Tate pairing on
$\textrm {Pic}^{0}(X)$
is the Néron–Tate pairing on
![]() $J(F)$
and
$J(F)$
and
![]() $\textrm {Pic}^{0}(X_{0}) \cong J(F)$
. The failure of these identities complicates the proof of Theorem 2 in the general case. In order to handle these complications, we now recall certain results from [Reference Gordon18, Reference Liu, Lorenzini and Raynaud30, Reference Liu, Lorenzini and Raynaud31, Reference Liu, Lorenzini and Raynaud32, Reference Geisser17, Reference Ulmer37, Reference Liu and Erné29].
$\textrm {Pic}^{0}(X_{0}) \cong J(F)$
. The failure of these identities complicates the proof of Theorem 2 in the general case. In order to handle these complications, we now recall certain results from [Reference Gordon18, Reference Liu, Lorenzini and Raynaud30, Reference Liu, Lorenzini and Raynaud31, Reference Liu, Lorenzini and Raynaud32, Reference Geisser17, Reference Ulmer37, Reference Liu and Erné29].
6.1 Index and Period
Let C be a smooth proper curve over a field K and
![]() $T=$
Spec K.
$T=$
Spec K.
Definition 32.
-
(i) The index
 $\delta _{K}$
of C over K is the least positive degree of a K-rational divisor on C. If is the degree map, then
$\delta _{K}$
of C over K is the least positive degree of a K-rational divisor on C. If is the degree map, then $$ \begin{align*}d: \textrm{Pic}(C) \to \mathbb Z\end{align*} $$
$$ \begin{align*}d: \textrm{Pic}(C) \to \mathbb Z\end{align*} $$
 $\delta _{K} = [\textrm {Coker}(d)]$
. The kernel of d is
$\delta _{K} = [\textrm {Coker}(d)]$
. The kernel of d is
 $\textrm {Pic}^{0}(C)$
.
$\textrm {Pic}^{0}(C)$
.
-
(ii) The period
 $\delta ^{\prime }_{K}$
of C over K is the least positive degree of a K-rational divisor class on C.
$\delta ^{\prime }_{K}$
of C over K is the least positive degree of a K-rational divisor class on C.
6.2 Curves over local and global fields [Reference Bosch and Liu3, Reference Liu, Lorenzini and Raynaud30]
Let K be a p-adic field with ring of integers
![]() ${\mathcal O}_{K}$
and residue field
${\mathcal O}_{K}$
and residue field
![]() $k(v) = \mathbb F_{q}$
. Write
$k(v) = \mathbb F_{q}$
. Write
![]() $T = \text {Spec}~{\mathcal O}_{K}$
and
$T = \text {Spec}~{\mathcal O}_{K}$
and
![]() $v: \text {Spec}~\mathbb F_{q} \to T$
for the closed point of T. Let
$v: \text {Spec}~\mathbb F_{q} \to T$
for the closed point of T. Let
![]() $f: C \to T$
be a flat projective morphism with C regular,
$f: C \to T$
be a flat projective morphism with C regular,
![]() $f_{*}{\mathcal O}_{C} = {\mathcal O}_{T}$
and
$f_{*}{\mathcal O}_{C} = {\mathcal O}_{T}$
and
![]() $C_{K} \to \text {Spec}~K$
a geometrically connected smooth curve of genus
$C_{K} \to \text {Spec}~K$
a geometrically connected smooth curve of genus
![]() $g>0$
. Let
$g>0$
. Let
![]() $\mathcal N$
be the Néron model of the Jacobian J of
$\mathcal N$
be the Néron model of the Jacobian J of
![]() $C_{K}$
. We write
$C_{K}$
. We write
![]() $\Phi _{v}=\pi _{0}(\mathcal N_{v})$
for the finite group scheme of connected components of the special fibre
$\Phi _{v}=\pi _{0}(\mathcal N_{v})$
for the finite group scheme of connected components of the special fibre
![]() $\mathcal N_{v}$
over v and
$\mathcal N_{v}$
over v and
![]() $c_{v} $
is the order of
$c_{v} $
is the order of
![]() $\Phi _{v}(k(v))$
.
$\Phi _{v}(k(v))$
.
Consider the map
![]() $Lie~(\phi ): R^{1}f_{*} {\mathcal O}_{C} \to Lie~\mathcal N$
of coherent sheaves on T and the induced map on T-points
$Lie~(\phi ): R^{1}f_{*} {\mathcal O}_{C} \to Lie~\mathcal N$
of coherent sheaves on T and the induced map on T-points
We will need the following result in Section 7.
Theorem 33 [Reference Liu, Lorenzini and Raynaud30, Theorem 3.1]
-
(i) The kernel of
 $\text {Lie}~(\phi )$
is the torsion subgroup of
$\text {Lie}~(\phi )$
is the torsion subgroup of
 $H^{1}(C, {\mathcal O}_{C})$
.
$H^{1}(C, {\mathcal O}_{C})$
. -
(ii) The kernel and cokernel of
 $Lie~(\phi )$
are torsion sheaves on T of the same length.
$Lie~(\phi )$
are torsion sheaves on T of the same length.
Let
![]() $\Gamma _{i}$
(
$\Gamma _{i}$
(
![]() $i\in I$
) be the irreducible components of the special fibre
$i\in I$
) be the irreducible components of the special fibre
![]() $C_{v}$
.
$C_{v}$
.
-
•
 $d_{i}$
is the multiplicity of
$d_{i}$
is the multiplicity of
 $\Gamma _{i}$
in
$\Gamma _{i}$
in
 $C_{v}$
.
$C_{v}$
. -
•
 $e_{i}$
is the geometric multiplicity of
$e_{i}$
is the geometric multiplicity of
 $\Gamma _{i}$
in
$\Gamma _{i}$
in
 $C_{v}$
.
$C_{v}$
. -
•
 $r_{i}$
is the number of irreducible components of
$r_{i}$
is the number of irreducible components of
 $\Gamma _{i} \times \mathrm {Spec}~\overline {\mathbb F_{q}}$
.
$\Gamma _{i} \times \mathrm {Spec}~\overline {\mathbb F_{q}}$
.
There are canonical maps [Reference Bosch and Liu3, Proposition 1.9]
![]() $\alpha _{C}: \mathbb Z^{I} \to \mathbb Z^{I}$
(defined using intersection on C) and
$\alpha _{C}: \mathbb Z^{I} \to \mathbb Z^{I}$
(defined using intersection on C) and
![]() $\beta _{C}: \mathbb Z^{I} \to \mathbb Z$
. Let d be the gcd of the set
$\beta _{C}: \mathbb Z^{I} \to \mathbb Z$
. Let d be the gcd of the set
![]() $\{d_{i}, i\in I\}$
and
$\{d_{i}, i\in I\}$
and
![]() $d^{\prime }$
be the gcd of the set
$d^{\prime }$
be the gcd of the set
![]() $\{r_{i}d_{i}, i\in I\}$
.
$\{r_{i}d_{i}, i\in I\}$
.
Theorem 34 [Reference Bosch and Liu3, Theorem 1.7, Corollary 1.12]
-
(i) There is an exact sequence
here $$ \begin{align*} 0 \to \frac{\textrm{Ker}~( \beta_{C})}{\textrm{Im}~(\alpha_{C})} \xrightarrow{h} \Phi_{v}(\mathbb F_{q}) \to \frac{cd\mathbb Z}{d^{\prime}\mathbb Z} \to 0;\end{align*} $$
$$ \begin{align*} 0 \to \frac{\textrm{Ker}~( \beta_{C})}{\textrm{Im}~(\alpha_{C})} \xrightarrow{h} \Phi_{v}(\mathbb F_{q}) \to \frac{cd\mathbb Z}{d^{\prime}\mathbb Z} \to 0;\end{align*} $$
 $c=1$
if
$c=1$
if
 $d^{\prime }$
divides
$d^{\prime }$
divides
 $g-1$
and
$g-1$
and
 $c=2$
otherwise.
$c=2$
otherwise.
-
(ii) If
 $C_{K}(K)$
is not empty, then
$C_{K}(K)$
is not empty, then
 $d^{\prime }=d$
and h is an isomorphism.
$d^{\prime }=d$
and h is an isomorphism.
It is known that [Reference Liu and Erné29, §9.1, Theorem 1.23] that the intersection pairing on
![]() $R_{v}$
$R_{v}$
 $$ \begin{align*}R_{v}:= \frac{\mathbb Z^{I}}{\mathbb Z} = \textrm{Coker}~(\mathbb Z \to \mathbb Z^{I}) \qquad 1\mapsto \sum_{i\in I} d_{i} \Gamma_{i}\end{align*} $$
$$ \begin{align*}R_{v}:= \frac{\mathbb Z^{I}}{\mathbb Z} = \textrm{Coker}~(\mathbb Z \to \mathbb Z^{I}) \qquad 1\mapsto \sum_{i\in I} d_{i} \Gamma_{i}\end{align*} $$
is negative definite. The following corollary of Theorem 34 and [Reference Bosch and Liu3, Theorem 1.11] on
![]() $\Delta (R_{v})$
(defined as in Subsection 2.3.5) is due to Flach–Siebel.
$\Delta (R_{v})$
(defined as in Subsection 2.3.5) is due to Flach–Siebel.
Corollary 35 (Flach–Siebel [Reference Flach and Siebel14, Lemma 17])
If
![]() $\delta _{v}$
is the index of
$\delta _{v}$
is the index of
![]() $C_{K}$
and
$C_{K}$
and
![]() $\delta ^{\prime }_{v}$
is the period of
$\delta ^{\prime }_{v}$
is the period of
![]() $C_{K}$
, then
$C_{K}$
, then
 $$ \begin{align*}\Delta(R_{v}) = \frac{c_{v}}{\delta_{v}~\cdot~\delta^{\prime}_{v}} \prod_{i\in I} r_{i}.\end{align*} $$
$$ \begin{align*}\Delta(R_{v}) = \frac{c_{v}}{\delta_{v}~\cdot~\delta^{\prime}_{v}} \prod_{i\in I} r_{i}.\end{align*} $$
In terms of the Arakelov intersection pairing on
![]() $R_{v}$
(see [Reference Faltings8, p. 390] or [Reference Gross20, (3.7)]), one has
$R_{v}$
(see [Reference Faltings8, p. 390] or [Reference Gross20, (3.7)]), one has
Lemma 36. Let
![]() $L_{v}(J, t)$
be the local L-factor of J as in (27). The zeta function
$L_{v}(J, t)$
be the local L-factor of J as in (27). The zeta function
 $$ \begin{align*}Z(C_{v},t) = \frac{P_{1}(C_{v},t)}{P_{0}(C_{v},t)~\cdot~P_{2}(C_{v},t)}\end{align*} $$
$$ \begin{align*}Z(C_{v},t) = \frac{P_{1}(C_{v},t)}{P_{0}(C_{v},t)~\cdot~P_{2}(C_{v},t)}\end{align*} $$
of
![]() $C_{v}$
satisfies
$C_{v}$
satisfies
 $$ \begin{align*}Z(C_{v},t) = \frac{L_{v}(J,t)}{(1-t)~\cdot~\prod_{i\in I}(1-{(qt)}^{r_{i}})}.\end{align*} $$
$$ \begin{align*}Z(C_{v},t) = \frac{L_{v}(J,t)}{(1-t)~\cdot~\prod_{i\in I}(1-{(qt)}^{r_{i}})}.\end{align*} $$
Proof. As
![]() $C_{K}$
is smooth projective and geometrically connected,
$C_{K}$
is smooth projective and geometrically connected,
![]() $C_{v}$
is geometrically connected. So
$C_{v}$
is geometrically connected. So
![]() $P_{0}(C_{v},t) = (1-t)$
.
$P_{0}(C_{v},t) = (1-t)$
.
We next show that
![]() $P_{1}(C_{v},t)$
equals
$P_{1}(C_{v},t)$
equals
![]() $L_{v}(J,t)$
of (27). For any prime
$L_{v}(J,t)$
of (27). For any prime
![]() $\ell $
coprime to q, the Kummer sequence and the perfect pairing (Poincaré duality)
$\ell $
coprime to q, the Kummer sequence and the perfect pairing (Poincaré duality)
 $$ \begin{align*}H^{1}_{et}(C_{K} \times \bar{K}, \mathbb Q_{\ell}) \times H^{1}_{et}(C_{K} \times \bar{K}, \mathbb Q_{\ell}(1) ) \xrightarrow{\cup} H^{2}_{et}(C_{K} \times \bar{K}, \mathbb Q_{\ell}(1) ) \cong \mathbb Q_{\ell}\end{align*} $$
$$ \begin{align*}H^{1}_{et}(C_{K} \times \bar{K}, \mathbb Q_{\ell}) \times H^{1}_{et}(C_{K} \times \bar{K}, \mathbb Q_{\ell}(1) ) \xrightarrow{\cup} H^{2}_{et}(C_{K} \times \bar{K}, \mathbb Q_{\ell}(1) ) \cong \mathbb Q_{\ell}\end{align*} $$
provide isomorphisms of
![]() $\textrm {Gal}(\bar {K}/K)$
-representations
$\textrm {Gal}(\bar {K}/K)$
-representations
So we obtain an isomorphism
of
![]() $\textrm {Gal}(\bar {K}/K) $
representations. Since
$\textrm {Gal}(\bar {K}/K) $
representations. Since
![]() $H^{1}_{et}(C_{v} \times \bar {\mathbb F}_{q}, \mathbb Q_{\ell })$
isomorphic to the subspace of
$H^{1}_{et}(C_{v} \times \bar {\mathbb F}_{q}, \mathbb Q_{\ell })$
isomorphic to the subspace of
![]() $H^{1}_{et}(C_{K} \times \bar {K}, \mathbb Q_{\ell })$
of invariants under the inertia subgroup [Reference Bloch1, Lemma 1.2], it follows from (46) and (27) that
$H^{1}_{et}(C_{K} \times \bar {K}, \mathbb Q_{\ell })$
of invariants under the inertia subgroup [Reference Bloch1, Lemma 1.2], it follows from (46) and (27) that
![]() $P_{1}(C_{v}, t)$
is
$P_{1}(C_{v}, t)$
is
![]() $L_{v}(J, t)$
.
$L_{v}(J, t)$
.
Finally, one has the elementary identity Footnote 4 [Reference Gordon18, Proposition 3.3]; see also [Reference Liu, Lorenzini and Raynaud30, p.484]
 $$ \begin{align*}P_{2}(C_{v},t) = \prod_{i\in I} (1-{(qt)}^{r_{i}}).\end{align*} $$
$$ \begin{align*}P_{2}(C_{v},t) = \prod_{i\in I} (1-{(qt)}^{r_{i}}).\end{align*} $$
This completes the proof.
6.3 Relating
 and
and
 $\textrm {Br}(X)$
$\textrm {Br}(X)$
For any arithmetic surface
![]() $X \to S$
, let
$X \to S$
, let
![]() $\delta $
be the index of
$\delta $
be the index of
![]() $X_{0}$
over F and
$X_{0}$
over F and
![]() $\alpha $
be the order of the (finite) cokernel of the natural map
$\alpha $
be the order of the (finite) cokernel of the natural map
![]() $\textrm {Pic}^{0}(X_{0}) \hookrightarrow J(F)$
. For any finite place v of S, we put
$\textrm {Pic}^{0}(X_{0}) \hookrightarrow J(F)$
. For any finite place v of S, we put
![]() $\delta _{v}$
and
$\delta _{v}$
and
![]() $\delta ^{\prime }_{v}$
for the (local) index and period of
$\delta ^{\prime }_{v}$
for the (local) index and period of
![]() $X\times F_{v}$
over the local field
$X\times F_{v}$
over the local field
![]() $F_{v}$
. The following result is due to Geisser [Reference Geisser17, Theorem 1.1]; there is also a recent proof by Flach-Siebel [Reference Flach and Siebel14].
$F_{v}$
. The following result is due to Geisser [Reference Geisser17, Theorem 1.1]; there is also a recent proof by Flach-Siebel [Reference Flach and Siebel14].
Theorem 37. Assume that
![]() $\text {Br}(X)$
is finite. The following equality holds (up to powers of
$\text {Br}(X)$
is finite. The following equality holds (up to powers of
![]() $2$
):
$2$
):

7 The proof of the main theorem in the general case
7.1 Preliminary steps
We are in a position to prove Theorem 2 in the general case. Let
![]() $\Sigma =\{v\in S~|~X_{v}~\textrm {is~not~smooth}\}$
; let
$\Sigma =\{v\in S~|~X_{v}~\textrm {is~not~smooth}\}$
; let
![]() $G_{v}$
denote the set of irreducible components of
$G_{v}$
denote the set of irreducible components of
![]() $X_{v}$
.
$X_{v}$
.
Lemma 38. If
 $$ \begin{align*} Q_{2}(s) = \prod_{v \in \Sigma} \frac{(1-q_{v}^{1-s})}{\prod_{i\in G_{v}} (1-q_{v}^{{r_{i}} (1-s)})},\end{align*} $$
$$ \begin{align*} Q_{2}(s) = \prod_{v \in \Sigma} \frac{(1-q_{v}^{1-s})}{\prod_{i\in G_{v}} (1-q_{v}^{{r_{i}} (1-s)})},\end{align*} $$
then
 $$ \begin{align} Q_{2}^{*}(1) &= \frac{1}{\prod_{v\in \Sigma} ( (\log q_{v})^{\#G_{v}-1}~\cdot~\prod_{i\in G_{v}} r_{i})} = \prod_{v\in \Sigma}\frac{c_{v}}{\Delta_{ar}(R_{v})~.\delta_{v}~\cdot~\delta^{\prime}_{v}} = P_{J,fin} \nonumber \\[3pt] & \quad \cdot~\prod_{v\in \Sigma}\frac{1}{\Delta_{ar}(R_{v})~.\delta_{v}~\cdot~\delta^{\prime}_{v}}.\end{align} $$
$$ \begin{align} Q_{2}^{*}(1) &= \frac{1}{\prod_{v\in \Sigma} ( (\log q_{v})^{\#G_{v}-1}~\cdot~\prod_{i\in G_{v}} r_{i})} = \prod_{v\in \Sigma}\frac{c_{v}}{\Delta_{ar}(R_{v})~.\delta_{v}~\cdot~\delta^{\prime}_{v}} = P_{J,fin} \nonumber \\[3pt] & \quad \cdot~\prod_{v\in \Sigma}\frac{1}{\Delta_{ar}(R_{v})~.\delta_{v}~\cdot~\delta^{\prime}_{v}}.\end{align} $$
Proof. The first equality is clear; the second uses Corollary 35; the third follows from (26) using
![]() $c_{v} =1$
for
$c_{v} =1$
for
![]() $v \notin \Sigma $
.
$v \notin \Sigma $
.
Proposition 39. One has
 $$ \begin{align*} \chi(B(1,1)) = \frac{P_{J, fin}}{P_{J}} = \frac{1}{P_{J,\infty}}= \frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}.\end{align*} $$
$$ \begin{align*} \chi(B(1,1)) = \frac{P_{J, fin}}{P_{J}} = \frac{1}{P_{J,\infty}}= \frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}.\end{align*} $$
Proof. One has the isomorphism of integral structures (its Euler characteristic is 1)
 $$ \begin{align*}H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}.\end{align*} $$
$$ \begin{align*}H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}.\end{align*} $$
As the notion of Néron model is local on the base [Reference Bosch, Lütkebohmert and Raynaud4, Proposition 4, page 13], Theorem 33 shows that the kernel and cokernel of
![]() $\text {Lie}(\phi ): H^{1}(X, \mathcal O) \to {\textrm {Lie}}(\mathcal J)$
are torsion
$\text {Lie}(\phi ): H^{1}(X, \mathcal O) \to {\textrm {Lie}}(\mathcal J)$
are torsion
![]() ${\mathcal O}_{F}$
-modules of the same length and the kernel is exactly the torsion of
${\mathcal O}_{F}$
-modules of the same length and the kernel is exactly the torsion of
![]() $H^{1}(X,{\mathcal O}_{X})$
. This implies that the Euler characteristic of
$H^{1}(X,{\mathcal O}_{X})$
. This implies that the Euler characteristic of
 $$ \begin{align*}H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C\xrightarrow{{\textrm{Lie}}{(\phi})} {\textrm{Lie}}(\mathcal J)\otimes_{\mathbb Z}\mathbb C\end{align*} $$
$$ \begin{align*}H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C\xrightarrow{{\textrm{Lie}}{(\phi})} {\textrm{Lie}}(\mathcal J)\otimes_{\mathbb Z}\mathbb C\end{align*} $$
is 1:
![]() $\chi (\text {Lie}(\phi )) =1$
. Here the integral structures are
$\chi (\text {Lie}(\phi )) =1$
. Here the integral structures are
![]() $(H^{1}(X, \mathcal O), [H^{1}(X, \mathcal O)_{tor}])$
and
$(H^{1}(X, \mathcal O), [H^{1}(X, \mathcal O)_{tor}])$
and
![]() $({\textrm {Lie}}(\mathcal J), 1)$
. We obtain that the Euler characteristic of
$({\textrm {Lie}}(\mathcal J), 1)$
. We obtain that the Euler characteristic of
 $$ \begin{align*} H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\gamma_{X}} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C\end{align*} $$
$$ \begin{align*} H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\gamma_{X}} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C\end{align*} $$
is equal to that of
 $$ \begin{align*}\gamma_{\mathcal J}: H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim}H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\gamma_{X}} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C\xrightarrow{{\textrm{Lie}}{(\phi})} {\textrm{Lie}}(\mathcal J)\otimes_{\mathbb Z}\mathbb C.\end{align*} $$
$$ \begin{align*}\gamma_{\mathcal J}: H^{1}_{B}(J_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim}H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\gamma_{X}} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C\xrightarrow{{\textrm{Lie}}{(\phi})} {\textrm{Lie}}(\mathcal J)\otimes_{\mathbb Z}\mathbb C.\end{align*} $$
Proposition 25 and Theorem 23 show
 $$ \begin{align} \chi(\gamma_{X}) = \chi(\gamma_{\mathcal J}) = \frac{P_{J,\infty}(\eta)~\cdot~\mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}{{\sqrt{|d_{F}|}}^{g}}.\end{align} $$
$$ \begin{align} \chi(\gamma_{X}) = \chi(\gamma_{\mathcal J}) = \frac{P_{J,\infty}(\eta)~\cdot~\mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}{{\sqrt{|d_{F}|}}^{g}}.\end{align} $$
Our convention for
![]() $B(1,1)$
is that
$B(1,1)$
is that
![]() $\textrm {Ker}(\gamma _{M})$
is in even degree, say, degree 0. Thus,
$\textrm {Ker}(\gamma _{M})$
is in even degree, say, degree 0. Thus,
 $$ \begin{align*}\underset{\textrm{degree 1}}{H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}} \to \underset{\textrm{degree 2}}{H^{1}(X, \mathcal O)\otimes \mathbb C}, \qquad det (B(1,1)) = \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~\cdot~\mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})} = \chi(B(1,1)). \end{align*} $$
$$ \begin{align*}\underset{\textrm{degree 1}}{H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C}} \to \underset{\textrm{degree 2}}{H^{1}(X, \mathcal O)\otimes \mathbb C}, \qquad det (B(1,1)) = \frac{{\sqrt{|d_{F}|}}^{g}}{P_{J,\infty}(\eta)~\cdot~\mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})} = \chi(B(1,1)). \end{align*} $$
7.2 Global index
Since X is regular, the natural map
![]() $ \textrm {Pic}(X) \to \textrm {Pic}(X_{0})$
is surjective: a natural section (as sets) is provided by sending a divisor on
$ \textrm {Pic}(X) \to \textrm {Pic}(X_{0})$
is surjective: a natural section (as sets) is provided by sending a divisor on
![]() $X_{0}$
to its Zariski closure in X. So the index
$X_{0}$
to its Zariski closure in X. So the index
![]() $\delta $
of
$\delta $
of
![]() $X_{0}$
over F is the order of the cokernel of the composite map
$X_{0}$
over F is the order of the cokernel of the composite map
 $\textrm {Pic}(X) \to \textrm {Pic}(X_{0}) \xrightarrow {d} \mathbb Z$
.
$\textrm {Pic}(X) \to \textrm {Pic}(X_{0}) \xrightarrow {d} \mathbb Z$
.
7.2.1 Calculation of
 $\chi (C(1))$
$\chi (C(1))$
The torsion in
![]() $C(1)$
of (22) satisfies
$C(1)$
of (22) satisfies
 $$ \begin{align} \chi(C(1)_{tor}) = \frac{w~\cdot~[Br(X)]} {[\textrm{Pic}(X)_{tor}]~\cdot~[\textrm{Pic}(X)_{tor}]}.\end{align} $$
$$ \begin{align} \chi(C(1)_{tor}) = \frac{w~\cdot~[Br(X)]} {[\textrm{Pic}(X)_{tor}]~\cdot~[\textrm{Pic}(X)_{tor}]}.\end{align} $$
We can rewrite
![]() $C(1)_{\mathbb C}$
as
$C(1)_{\mathbb C}$
as
 $$ \begin{align} 0 &\to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \underset{degree~2}{\textrm{Hom}(\textrm{Pic}(X), \mathbb C)} \to \underset{degree~3}{{\textrm{Pic}(X)}\otimes\mathbb C} \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \nonumber\\[3pt] &\to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb C)} \to 0. \end{align} $$
$$ \begin{align} 0 &\to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \underset{degree~2}{\textrm{Hom}(\textrm{Pic}(X), \mathbb C)} \to \underset{degree~3}{{\textrm{Pic}(X)}\otimes\mathbb C} \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \nonumber\\[3pt] &\to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb C)} \to 0. \end{align} $$
Using the exact sequence
 $$ \begin{align} 0 \to \textrm{Pic}^{0}(X) \to \textrm{Pic}(X) \xrightarrow{d} \mathbb Z \to \frac{\mathbb Z}{\delta\mathbb Z} \to 0,\end{align} $$
$$ \begin{align} 0 \to \textrm{Pic}^{0}(X) \to \textrm{Pic}(X) \xrightarrow{d} \mathbb Z \to \frac{\mathbb Z}{\delta\mathbb Z} \to 0,\end{align} $$
the sequence
![]() $C(1)$
breaks up into
$C(1)$
breaks up into
-
• the sequence (14) with determinant R
 $$ \begin{align*}0 \to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \underset{degree~2}{\textrm{Hom}(\mathbb Z, \mathbb C)} \to 0;\end{align*} $$
$$ \begin{align*}0 \to \underset{degree~0}{{\mathcal O}_{F}^{\times}\otimes\mathbb C} \to \underset{degree~1}{\textrm{Coker}(\gamma_{M_{0}})} \to \underset{degree~2}{\textrm{Hom}(\mathbb Z, \mathbb C)} \to 0;\end{align*} $$
-
• the sequence with determinant
 $\delta $
$\delta $
 $$ \begin{align*}0 \to \textrm{Hom}(\mathbb Z, \mathbb C) \to \textrm{Hom}(\textrm{Pic}(X), \mathbb C) \to \textrm{Hom}(\textrm{Pic}^{0}(X), \mathbb C) \to 0; \end{align*} $$
$$ \begin{align*}0 \to \textrm{Hom}(\mathbb Z, \mathbb C) \to \textrm{Hom}(\textrm{Pic}(X), \mathbb C) \to \textrm{Hom}(\textrm{Pic}^{0}(X), \mathbb C) \to 0; \end{align*} $$
-
• and the sequence with determinant
 $det(\psi )$
where h is the Arakelov intersection pairing [Reference Lichtenbaum27, Conjecture 2.3.7] as in (11);
$det(\psi )$
where h is the Arakelov intersection pairing [Reference Lichtenbaum27, Conjecture 2.3.7] as in (11); $$ \begin{align*}h: \underset{degree~2}{\textrm{Hom}(\textrm{Pic}^{0}(X), \mathbb C)} \to \underset{degree~3}{{\textrm{Pic}^{0}(X)}\otimes\mathbb C} \end{align*} $$
$$ \begin{align*}h: \underset{degree~2}{\textrm{Hom}(\textrm{Pic}^{0}(X), \mathbb C)} \to \underset{degree~3}{{\textrm{Pic}^{0}(X)}\otimes\mathbb C} \end{align*} $$
-
• the sequence with determinant
 $\delta $
$\delta $
 $$ \begin{align*}0 \to \textrm{Pic}^{0}(X)\otimes \mathbb C \to \textrm{Pic}(X)\otimes \mathbb C \xrightarrow{d} \mathbb C \to 0;\end{align*} $$
$$ \begin{align*}0 \to \textrm{Pic}^{0}(X)\otimes \mathbb C \to \textrm{Pic}(X)\otimes \mathbb C \xrightarrow{d} \mathbb C \to 0;\end{align*} $$
-
• the sequence (12) with determinant R
 $$ \begin{align*} 0 \to \mathbb C \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb Z)\otimes \mathbb C} \to 0.\end{align*} $$
$$ \begin{align*} 0 \to \mathbb C \to \underset{degree~4}{\textrm{Ker}(\gamma_{M_{2}})} \to \underset{degree~5}{\textrm{Hom}({\mathcal O}_{F}^{\times}, \mathbb Z)\otimes \mathbb C} \to 0.\end{align*} $$
It follows from (52) that, in (51), the image of the lattice in degree 3 has index
![]() $\delta $
in the lattice in degree 4; dually, the image of the lattice in degree 1 has index
$\delta $
in the lattice in degree 4; dually, the image of the lattice in degree 1 has index
![]() $\delta $
in the lattice in degree 3. Thus,
$\delta $
in the lattice in degree 3. Thus,
 $$ \begin{align*}det(C(1)) = \frac{R~\cdot~R}{\delta~\cdot~\delta~\cdot~det(h)}.\end{align*} $$
$$ \begin{align*}det(C(1)) = \frac{R~\cdot~R}{\delta~\cdot~\delta~\cdot~det(h)}.\end{align*} $$
So
![]() $ \chi (C(1)) $
is given as
$ \chi (C(1)) $
is given as
 $$ \begin{align} &= \frac{det(C(1))}{\chi(C(1)_{tor})} = \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~[\textrm{Pic}^{0}(X)_{tor}]^{2}}~\cdot~\frac{[\textrm{Pic}^{0}(X)_{tor}]^{2}}{w~\cdot~[\textrm{Br}(X)]} \nonumber \\ &= \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]},\end{align} $$
$$ \begin{align} &= \frac{det(C(1))}{\chi(C(1)_{tor})} = \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~[\textrm{Pic}^{0}(X)_{tor}]^{2}}~\cdot~\frac{[\textrm{Pic}^{0}(X)_{tor}]^{2}}{w~\cdot~[\textrm{Br}(X)]} \nonumber \\ &= \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]},\end{align} $$
where, as in Subsection 2.3.5,
 $$ \begin{align} \Delta_{ar}(\textrm{Pic}^{0}(X)) = \frac{det(h)}{[\textrm{Pic}^{0}(X)_{tor}]^{2}}.\end{align} $$
$$ \begin{align} \Delta_{ar}(\textrm{Pic}^{0}(X)) = \frac{det(h)}{[\textrm{Pic}^{0}(X)_{tor}]^{2}}.\end{align} $$
Our next task is to calculate
![]() $\Delta _{ar}(\textrm {Pic}^{0}(X))$
and relate it to the Néron–Tate pairing (56) on
$\Delta _{ar}(\textrm {Pic}^{0}(X))$
and relate it to the Néron–Tate pairing (56) on
![]() $J(F)$
.
$J(F)$
.
7.2.2 Calculation of
 $\Delta _{ar}(\textrm {Pic}^{0}(X))$
$\Delta _{ar}(\textrm {Pic}^{0}(X))$
This is based on localisation sequences on X and S.
Let
![]() $U = S - \Sigma $
. So the map
$U = S - \Sigma $
. So the map
![]() $X_{U} = \pi ^{-1}(U) \to U$
is smooth. For any finite
$X_{U} = \pi ^{-1}(U) \to U$
is smooth. For any finite
![]() $\Sigma ^{\prime } \subset S$
containing
$\Sigma ^{\prime } \subset S$
containing
![]() $\Sigma $
, we put
$\Sigma $
, we put
![]() $U^{\prime } = S - \Sigma ^{\prime }$
and
$U^{\prime } = S - \Sigma ^{\prime }$
and
![]() $X_{U^{\prime }} = X - \pi ^{-1}(U^{\prime })$
.
$X_{U^{\prime }} = X - \pi ^{-1}(U^{\prime })$
.
Lemma 40.
-
(i) The maps
are injective. $$ \begin{align*}\textrm{Pic}(S) \to \textrm{Pic}(X), \qquad \textrm{Pic}(U^{\prime}) \to \textrm{Pic}(X_{U^{\prime}})\end{align*} $$
$$ \begin{align*}\textrm{Pic}(S) \to \textrm{Pic}(X), \qquad \textrm{Pic}(U^{\prime}) \to \textrm{Pic}(X_{U^{\prime}})\end{align*} $$
-
(ii) There is an exact sequence
(55) $$ \begin{align} 0 \to \oplus_{v\in \Sigma} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}^{0} (X)}{\textrm{Pic}(S)} \to \textrm{Pic}^{0} ( X_{0}) \to 0.\end{align} $$
$$ \begin{align} 0 \to \oplus_{v\in \Sigma} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}^{0} (X)}{\textrm{Pic}(S)} \to \textrm{Pic}^{0} ( X_{0}) \to 0.\end{align} $$
Proof.
-
(i) From the Leray spectral sequence for
 $\pi : X\to S$
and the étale sheaf
$\pi : X\to S$
and the étale sheaf
 $\mathbb G_{m}$
on X, we get the exact sequence Now use that
$\mathbb G_{m}$
on X, we get the exact sequence Now use that $$ \begin{align*} 0 \to H^{1}(S, \pi_{*} \mathbb G_{m}) \to H^{1}(X, \mathbb G_{m}) \to H^{0}(S, R^{1}\pi_{*}\mathbb G {}_{m}) \to \textrm{Br}(S).\end{align*} $$
$$ \begin{align*} 0 \to H^{1}(S, \pi_{*} \mathbb G_{m}) \to H^{1}(X, \mathbb G_{m}) \to H^{0}(S, R^{1}\pi_{*}\mathbb G {}_{m}) \to \textrm{Br}(S).\end{align*} $$
 $\pi _{*}\mathbb G_{m}$
is the sheaf
$\pi _{*}\mathbb G_{m}$
is the sheaf
 $\mathbb G_{m}$
on S. This provides the injectivity of the first map. A similar argument provides the injectivity of the second.
$\mathbb G_{m}$
on S. This provides the injectivity of the first map. A similar argument provides the injectivity of the second.
-
(ii) We can compare the localisation sequences for
 $X_{U^{\prime }} \subset X$
and
$X_{U^{\prime }} \subset X$
and
 $U^{\prime } \subset S$
$U^{\prime } \subset S$

Note that S and X are regular and for any regular scheme Y, one has an isomorphism
![]() $\textrm {Cl}(Y) = \textrm {Pic}(Y)$
between the class group and the Picard group. The natural map between the localisation sequences is injective on all terms and, by assumption, is an isomorphism on the first and second terms. This provides the exact sequence
$\textrm {Cl}(Y) = \textrm {Pic}(Y)$
between the class group and the Picard group. The natural map between the localisation sequences is injective on all terms and, by assumption, is an isomorphism on the first and second terms. This provides the exact sequence
 $$ \begin{align*}0 \to \oplus_{v\in \Sigma^{\prime}} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}(X)}{\textrm{Pic}(S)} \to \frac{\textrm{Pic}(X_{U^{\prime}})}{\textrm{Pic}(U^{\prime})} \to 0.\end{align*} $$
$$ \begin{align*}0 \to \oplus_{v\in \Sigma^{\prime}} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}(X)}{\textrm{Pic}(S)} \to \frac{\textrm{Pic}(X_{U^{\prime}})}{\textrm{Pic}(U^{\prime})} \to 0.\end{align*} $$
In particular, we get this sequence for
![]() $\Sigma $
and U. Using (52), we obtain the exact sequence
$\Sigma $
and U. Using (52), we obtain the exact sequence
 $$ \begin{align*}0 \to \oplus_{v\in \Sigma} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)} \to \frac{\textrm{Pic}^{0}(X_{U})}{\textrm{Pic}(U)} \to 0.\end{align*} $$
$$ \begin{align*}0 \to \oplus_{v\in \Sigma} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)} \to \frac{\textrm{Pic}^{0}(X_{U})}{\textrm{Pic}(U)} \to 0.\end{align*} $$
By assumption,
![]() $X_{v}$
is geometrically irreducible for any
$X_{v}$
is geometrically irreducible for any
![]() $v \notin \Sigma $
. So for any
$v \notin \Sigma $
. So for any
![]() $U^{\prime } = S - \Sigma ^{\prime }$
with
$U^{\prime } = S - \Sigma ^{\prime }$
with
![]() $U^{\prime } \subset U$
, the induced maps
$U^{\prime } \subset U$
, the induced maps
 $$ \begin{align*}\frac{\textrm{Pic}^{0}(X_{U})}{\textrm{Pic}(U)}\to \frac{\textrm{Pic}^{0}(X_{U^{\prime}})}{\textrm{Pic}(U^{\prime})}\end{align*} $$
$$ \begin{align*}\frac{\textrm{Pic}^{0}(X_{U})}{\textrm{Pic}(U)}\to \frac{\textrm{Pic}^{0}(X_{U^{\prime}})}{\textrm{Pic}(U^{\prime})}\end{align*} $$
are isomorphisms. Taking the limit over
![]() $\Sigma ^{\prime }$
gives us an exact sequence
$\Sigma ^{\prime }$
gives us an exact sequence
 $$ \begin{align*}0 \to \oplus_{v\in \Sigma} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}^{0} (X)}{\textrm{Pic}(S)} \to \textrm{Pic}^{0}(X_{0}) \to 0.\end{align*} $$
$$ \begin{align*}0 \to \oplus_{v\in \Sigma} \frac{ \mathbb Z^{G_{v}}}{\mathbb Z} \to \frac{\textrm{Pic}^{0} (X)}{\textrm{Pic}(S)} \to \textrm{Pic}^{0}(X_{0}) \to 0.\end{align*} $$
This proves the lemma.
For any
![]() $v \in S$
, recall
$v \in S$
, recall
![]() $\Delta _{ar}(R_{v})$
from Corollary 35, where
$\Delta _{ar}(R_{v})$
from Corollary 35, where
 $$ \begin{align*}R_{v} =\frac{\mathbb Z^{G_{v}}}{\mathbb Z}\end{align*} $$
$$ \begin{align*}R_{v} =\frac{\mathbb Z^{G_{v}}}{\mathbb Z}\end{align*} $$
and, as before,
![]() $G_{v}$
is the set of irreducible components of
$G_{v}$
is the set of irreducible components of
![]() $X_{v}$
. Let us define (see Subsection 2.3.5)
$X_{v}$
. Let us define (see Subsection 2.3.5)
 $$ \begin{align} \Delta_{NT}(J(F)) = \frac{\Theta_{NT}(J)}{ [ J(F)_{tor}]~\cdot~[J(F)_{tor}]} \end{align} $$
$$ \begin{align} \Delta_{NT}(J(F)) = \frac{\Theta_{NT}(J)}{ [ J(F)_{tor}]~\cdot~[J(F)_{tor}]} \end{align} $$
using the Néron–Tate pairing (35) on
![]() $J(F)$
, analogous to
$J(F)$
, analogous to
![]() $\Delta _{ar}(\textrm {Pic}^{0}(X))$
from (54).
$\Delta _{ar}(\textrm {Pic}^{0}(X))$
from (54).
Proposition 41. If
![]() $\alpha $
is the order of the cokernel of the natural map
$\alpha $
is the order of the cokernel of the natural map
![]() $\textrm {Pic}^{0}(X_{0}) \hookrightarrow J(F)$
, then one has
$\textrm {Pic}^{0}(X_{0}) \hookrightarrow J(F)$
, then one has
 $$ \begin{align} \Delta_{ar}(\textrm{Pic}^{0}(X))= \pm \frac{\alpha^{2}}{h^{2}}~\cdot~\Delta_{NT}(J(F))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v}).\end{align} $$
$$ \begin{align} \Delta_{ar}(\textrm{Pic}^{0}(X))= \pm \frac{\alpha^{2}}{h^{2}}~\cdot~\Delta_{NT}(J(F))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v}).\end{align} $$
Proof. By [Reference Hriljac21, Proposition 3.3], the Arakelov intersection pairing h is negative-definite on
![]() $\textrm {Pic}^{0}(X)\otimes \mathbb Q$
and there exists a map
$\textrm {Pic}^{0}(X)\otimes \mathbb Q$
and there exists a map
![]() $\kappa : \textrm {Pic}^{0}(X_{0}) \to \textrm {Pic}^{0}(X)$
such that
$\kappa : \textrm {Pic}^{0}(X_{0}) \to \textrm {Pic}^{0}(X)$
such that
gives the intersection pairing on
![]() $\textrm {Pic}^{0}(X_{0})$
which, by Faltings–Hriljac [Reference Faltings8], [Reference Hriljac21, Theorem 3.1], is the negative of the Néron–Tate pairing (35) on
$\textrm {Pic}^{0}(X_{0})$
which, by Faltings–Hriljac [Reference Faltings8], [Reference Hriljac21, Theorem 3.1], is the negative of the Néron–Tate pairing (35) on
![]() $J(F)$
. Note that this means
$J(F)$
. Note that this means
So the sequence (55) splits over
![]() $\mathbb Q$
as an orthogonal direct sum with respect to the Arakelov intersection pairing
$\mathbb Q$
as an orthogonal direct sum with respect to the Arakelov intersection pairing
 $$ \begin{align} (\textrm{Pic}^{0} ( X_{0})\otimes\mathbb Q)~\oplus~(\underset{v\in \Sigma}{\oplus} \frac{ \mathbb Q^{G_{v}}}{\mathbb Q}) \cong \textrm{Pic}^{0} (X)\otimes\mathbb Q.\end{align} $$
$$ \begin{align} (\textrm{Pic}^{0} ( X_{0})\otimes\mathbb Q)~\oplus~(\underset{v\in \Sigma}{\oplus} \frac{ \mathbb Q^{G_{v}}}{\mathbb Q}) \cong \textrm{Pic}^{0} (X)\otimes\mathbb Q.\end{align} $$
The map
![]() $\kappa $
is defined as follows: given any element y of
$\kappa $
is defined as follows: given any element y of
![]() $\textrm {Pic}^{0} ( X_{0})$
, consider its Zariski closure
$\textrm {Pic}^{0} ( X_{0})$
, consider its Zariski closure
![]() $\bar {y}$
in X. As the intersection pairing is negative-definite [Reference Liu and Erné29, §9.1, Theorem 1.23] on
$\bar {y}$
in X. As the intersection pairing is negative-definite [Reference Liu and Erné29, §9.1, Theorem 1.23] on
![]() $R_{v}$
, the linear mapping
$R_{v}$
, the linear mapping
![]() $R_{v} \to \mathbb Z$
defined by
$R_{v} \to \mathbb Z$
defined by
![]() $z \mapsto z.\bar {y}$
is represented by a unique element
$z \mapsto z.\bar {y}$
is represented by a unique element
![]() $\kappa _{v}(y) \in R_{v}\otimes \mathbb Q$
. Clearly, the element
$\kappa _{v}(y) \in R_{v}\otimes \mathbb Q$
. Clearly, the element
 $$ \begin{align*}\kappa(y) = \bar{y} - \sum_{v\in \Sigma} \kappa_{v}(y) \end{align*} $$
$$ \begin{align*}\kappa(y) = \bar{y} - \sum_{v\in \Sigma} \kappa_{v}(y) \end{align*} $$
is orthogonal to
![]() $\oplus _{v\in \Sigma }R_{v} \subset \textrm {Pic}^{0}(X)$
; so the assignment
$\oplus _{v\in \Sigma }R_{v} \subset \textrm {Pic}^{0}(X)$
; so the assignment
![]() $y \mapsto \kappa (y)$
provides (59).
$y \mapsto \kappa (y)$
provides (59).
Now (7) shows
 $$ \begin{align*} \Delta_{ar}(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)})= \Delta_{ar}(\textrm{Pic}^{0}(X_{0} ))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v}).\end{align*} $$
$$ \begin{align*} \Delta_{ar}(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)})= \Delta_{ar}(\textrm{Pic}^{0}(X_{0} ))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v}).\end{align*} $$
Using
![]() $h = [\textrm {Pic}(S)]$
, this becomes
$h = [\textrm {Pic}(S)]$
, this becomes
 $$ \begin{align}\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~ {h^{2}} = \Delta_{ar}(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)})= \Delta_{ar}(\textrm{Pic}^{0}(X_{0} ))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v}).\end{align} $$
$$ \begin{align}\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~ {h^{2}} = \Delta_{ar}(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)})= \Delta_{ar}(\textrm{Pic}^{0}(X_{0} ))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v}).\end{align} $$
As
![]() $\textrm {Pic}^{0}(X_{0}) \hookrightarrow J(F)$
is a subgroup of index
$\textrm {Pic}^{0}(X_{0}) \hookrightarrow J(F)$
is a subgroup of index
![]() $\alpha $
, we see
$\alpha $
, we see
![]() $ \Delta _{ar}(\textrm {Pic}^{0}(X_{0} )) = \alpha ^{2} \Delta _{ar}(J(F)) = \pm \alpha ^{2}\cdot \Delta _{NT}(J(F))$
.
$ \Delta _{ar}(\textrm {Pic}^{0}(X_{0} )) = \alpha ^{2} \Delta _{ar}(J(F)) = \pm \alpha ^{2}\cdot \Delta _{NT}(J(F))$
.
7.3 The zeta function of X
Our first step is to rewrite the zeta function
![]() $\zeta (X,s)$
$\zeta (X,s)$
 $$ \begin{align*} \zeta(X,s) = \prod_{v \in S}\zeta(X_{v}, q_{v}^{-s}), \qquad \zeta(X_{v}, t) = \frac{P_{1}(X_{v},t)}{P_{0}(X_{v}, t) P_{2}(X_{v}, t)}.\end{align*} $$
$$ \begin{align*} \zeta(X,s) = \prod_{v \in S}\zeta(X_{v}, q_{v}^{-s}), \qquad \zeta(X_{v}, t) = \frac{P_{1}(X_{v},t)}{P_{0}(X_{v}, t) P_{2}(X_{v}, t)}.\end{align*} $$
Proposition 42. One has
 $$ \begin{align} \zeta(X,s) = \frac{\zeta(S,s)~\cdot~\zeta(S, s-1)}{L(J,s)}~\cdot~Q_{2}(s), \qquad \zeta^{*}(X,1) = \frac{\zeta^{*}(S,1)~\cdot~\zeta^{*}(S, 0)}{L^{*}(J,1)}~\cdot~Q_{2}^{*}(1).\end{align} $$
$$ \begin{align} \zeta(X,s) = \frac{\zeta(S,s)~\cdot~\zeta(S, s-1)}{L(J,s)}~\cdot~Q_{2}(s), \qquad \zeta^{*}(X,1) = \frac{\zeta^{*}(S,1)~\cdot~\zeta^{*}(S, 0)}{L^{*}(J,1)}~\cdot~Q_{2}^{*}(1).\end{align} $$
Proof. By Lemma 36, we see that
-
(i) the factors
 $P_{0}$
combine to give
$P_{0}$
combine to give
 $\zeta (S,s)$
;
$\zeta (S,s)$
; -
(ii) the factors
 $P_{1}$
combine to give
$P_{1}$
combine to give
 $L(J,s)$
;
$L(J,s)$
; -
(iii)
 $P_{2}(X_{v},t)$
is the expected factor
$P_{2}(X_{v},t)$
is the expected factor
 $(1-q_{v}t)$
for
$(1-q_{v}t)$
for
 $v\notin \Sigma $
; for
$v\notin \Sigma $
; for
 $v \in \Sigma $
and is given in Lemma 36. So
$v \in \Sigma $
and is given in Lemma 36. So  $$ \begin{align*}\prod_{v\in S}\frac{1}{P_{2}(X_{v},q_{v}^{-s}) } = Q_{2}(s)~\cdot~\prod_{v\in S} \frac{1}{1-q_{v}^{(1-s)}} = Q_{2}(s)~\cdot~\zeta(S, s-1). \\[-56pt] \end{align*} $$
$$ \begin{align*}\prod_{v\in S}\frac{1}{P_{2}(X_{v},q_{v}^{-s}) } = Q_{2}(s)~\cdot~\prod_{v\in S} \frac{1}{1-q_{v}^{(1-s)}} = Q_{2}(s)~\cdot~\zeta(S, s-1). \\[-56pt] \end{align*} $$
7.4 Completion of the proof of Theorem 2
We prove the main result of this article.
Proof
(of Theorem 2). We can restate Conjecture 20 for
![]() $J/F$
using (56) as
$J/F$
using (56) as

From Proposition 42, we see that Conjecture 20 for
![]() $J/F$
is equivalent to the equality
$J/F$
is equivalent to the equality

Conjecture 1 states that
 $$ \begin{align*} \zeta^{*}(X,1) = \chi(X,1) = \frac{\chi_{A,C}(X,1)}{\chi_{B}(X,1)} = \chi_{A}(X,1)~{\cdot}~\chi_{A^{\prime}}(X,1)~{\cdot}~\chi(C(1))~{\cdot}~\frac{\chi(B(1,1))}{\chi(B(0,1)) \chi(B(2,1))}.\end{align*} $$
$$ \begin{align*} \zeta^{*}(X,1) = \chi(X,1) = \frac{\chi_{A,C}(X,1)}{\chi_{B}(X,1)} = \chi_{A}(X,1)~{\cdot}~\chi_{A^{\prime}}(X,1)~{\cdot}~\chi(C(1))~{\cdot}~\frac{\chi(B(1,1))}{\chi(B(0,1)) \chi(B(2,1))}.\end{align*} $$
Using (24), (25), (19) and Proposition 39,
 $$ \begin{align*} \chi(B(0,1)) &= \frac{\sqrt{|d_{F}|}}{(2\pi )^{r_{2}}},\quad \chi(B(1,1)) = \frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})},\nonumber \\ \chi(B(2,1)) &=1= \chi_{A}(X,1), \quad \chi_{A^{\prime}}(X,1) = \frac{1}{w},\end{align*} $$
$$ \begin{align*} \chi(B(0,1)) &= \frac{\sqrt{|d_{F}|}}{(2\pi )^{r_{2}}},\quad \chi(B(1,1)) = \frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})},\nonumber \\ \chi(B(2,1)) &=1= \chi_{A}(X,1), \quad \chi_{A^{\prime}}(X,1) = \frac{1}{w},\end{align*} $$
we have
 $$ \begin{align} \chi(X,1) &= \frac{\chi_{A,C}(X,1)}{ \chi_{B}(X,1)} \notag\\[3pt] &= \chi_{A}(X,1)~\cdot~\chi_{A^{\prime}}(X,1)~\cdot~\chi(C(1))~\cdot~\frac{\chi(B(1,1))}{\chi(B(0,1)) \chi(B(2,1))} \notag\\[3pt] &= 1.~\frac{1}{w}~\cdot~\chi(C(1))~\cdot~\frac{(2\pi )^{r_{2}}}{\sqrt{|d_{F}|}} ~\cdot~\frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}\notag\\[3pt] &= \chi(C(1))~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}} ~\cdot~\frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}({\mathfrak a}_{\eta})}\notag\\[3pt] & \overset{(53)}{=} \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]}~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}} \cdot \frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ {\mathbb N}_{F/{\mathbb Q}}({\mathfrak a}_{\eta})}. \end{align} $$
$$ \begin{align} \chi(X,1) &= \frac{\chi_{A,C}(X,1)}{ \chi_{B}(X,1)} \notag\\[3pt] &= \chi_{A}(X,1)~\cdot~\chi_{A^{\prime}}(X,1)~\cdot~\chi(C(1))~\cdot~\frac{\chi(B(1,1))}{\chi(B(0,1)) \chi(B(2,1))} \notag\\[3pt] &= 1.~\frac{1}{w}~\cdot~\chi(C(1))~\cdot~\frac{(2\pi )^{r_{2}}}{\sqrt{|d_{F}|}} ~\cdot~\frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}(\mathfrak a_{\eta})}\notag\\[3pt] &= \chi(C(1))~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}} ~\cdot~\frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ \mathbb N_{F/{\mathbb Q}}({\mathfrak a}_{\eta})}\notag\\[3pt] & \overset{(53)}{=} \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]}~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}} \cdot \frac{|d_{F}|^{g/2}}{P_{J, \infty}(\eta)~\cdot~ {\mathbb N}_{F/{\mathbb Q}}({\mathfrak a}_{\eta})}. \end{align} $$
To prove Theorem 2, we need to show that
![]() $\chi (X,1)$
is equal to
$\chi (X,1)$
is equal to

Thus, we see that Theorem 2 follows if we prove that (neglecting powers of 2)

By (53), we have
 $$ \begin{align*}\chi(C(1)) = \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]}.\end{align*} $$
$$ \begin{align*}\chi(C(1)) = \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]}.\end{align*} $$
Thus, to prove Theorem 2, we only need to check if

We can verify this readily using Proposition 41, which says
 $$ \begin{align} \Delta_{ar}(\textrm{Pic}^{0}(X))= \frac{\alpha^{2}~\cdot~\Delta_{ar}(J(F))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v})}{h^{2}},\end{align} $$
$$ \begin{align} \Delta_{ar}(\textrm{Pic}^{0}(X))= \frac{\alpha^{2}~\cdot~\Delta_{ar}(J(F))~\cdot~\prod_{v\in\Sigma} \Delta_{ar}(R_{v})}{h^{2}},\end{align} $$
and Theorem 37, which says (note
![]() $\delta _{v} =1 = \delta ^{\prime }_{v}$
if
$\delta _{v} =1 = \delta ^{\prime }_{v}$
if
![]() $v \notin \Sigma $
)
$v \notin \Sigma $
)

This completes the proof of Theorem 2 in the general case.
Remark 43. Consider the case
![]() $g=0$
. As J is trivial, Theorem 2 says Conjecture 1 is true. Let us see directly that this is true (up to powers of 2): (63) shows that
$g=0$
. As J is trivial, Theorem 2 says Conjecture 1 is true. Let us see directly that this is true (up to powers of 2): (63) shows that
 $$ \begin{align*}\zeta^{*}(X,1) = \frac{2^{r_{1}} (2\pi)^{r_{2}}}{w \sqrt{|d_{F}|}}~\cdot~\frac{h^{2}~\cdot~R^{2}}{w} ~\cdot~\prod_{v\in \Sigma}~\frac{1}{\Delta_{ar}(R_{v})~\cdot~\delta_{v}~\cdot~\delta^{\prime}_{v}},\end{align*} $$
$$ \begin{align*}\zeta^{*}(X,1) = \frac{2^{r_{1}} (2\pi)^{r_{2}}}{w \sqrt{|d_{F}|}}~\cdot~\frac{h^{2}~\cdot~R^{2}}{w} ~\cdot~\prod_{v\in \Sigma}~\frac{1}{\Delta_{ar}(R_{v})~\cdot~\delta_{v}~\cdot~\delta^{\prime}_{v}},\end{align*} $$
 $$ \begin{align*}\chi(X,1) &= \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]}~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}} = \frac{h^{2}}{\alpha^{2}~\cdot~\prod_{v\in \Sigma}~{\Delta_{ar}(R_{v})}} \nonumber \\[3pt] & \quad \cdot~\frac{R^{2}}{\delta^{2}~\cdot~w~\cdot~[\textrm{Br}(X)]}~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}}.\end{align*} $$
$$ \begin{align*}\chi(X,1) &= \frac{R^{2}}{\delta^{2}~\cdot~\Delta_{ar}(\textrm{Pic}^{0}(X))~\cdot~w~\cdot~[\textrm{Br}(X)]}~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}} = \frac{h^{2}}{\alpha^{2}~\cdot~\prod_{v\in \Sigma}~{\Delta_{ar}(R_{v})}} \nonumber \\[3pt] & \quad \cdot~\frac{R^{2}}{\delta^{2}~\cdot~w~\cdot~[\textrm{Br}(X)]}~\cdot~\frac{(2\pi )^{r_{2}}}{w\sqrt{|d_{F}|}}.\end{align*} $$
As
![]() $\alpha $
,
$\alpha $
,
![]() $\delta _{v}$
,
$\delta _{v}$
,
![]() $\delta $
and
$\delta $
and
![]() $\delta ^{\prime }_{v}$
divide 2 and (66) shows that
$\delta ^{\prime }_{v}$
divide 2 and (66) shows that
![]() $[\textrm {Br}(X)]$
is a power of 2, it follows that the equality
$[\textrm {Br}(X)]$
is a power of 2, it follows that the equality
![]() $\zeta ^{*}(X,1) = \chi (X,1)$
is valid up to a finite power of 2.
$\zeta ^{*}(X,1) = \chi (X,1)$
is valid up to a finite power of 2.
7.5 Comparison with the Artin–Tate conjecture
Theorem 2 is the analogue for arithmetic surfaces of Conjecture (d) [Reference Tate36, p. 427] in the spirit of [Reference Lichtenbaum26]. More precisely, one has the following.
Theorem 44. Conjecture 1 for X is equivalent to the following identity (up to a finite power of 2):
 $$ \begin{align} \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1)}{\zeta^{*}(X,1)} = \chi(\gamma_{X})\cdot [\textrm{Br}(X)]\cdot \Delta_{ar}(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)}) \cdot \delta^{2}. \end{align} $$
$$ \begin{align} \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1)}{\zeta^{*}(X,1)} = \chi(\gamma_{X})\cdot [\textrm{Br}(X)]\cdot \Delta_{ar}(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)}) \cdot \delta^{2}. \end{align} $$
Here
![]() $\delta $
is the global index of X as in Subsection 7.2. The term
$\delta $
is the global index of X as in Subsection 7.2. The term
![]() $\chi (\gamma _{X})$
is an Archimedean period: it is the Euler characteristic (as in Subsection 2.3) of
$\chi (\gamma _{X})$
is an Archimedean period: it is the Euler characteristic (as in Subsection 2.3) of
 $$ \begin{align*} \gamma_{X}: H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C \end{align*} $$
$$ \begin{align*} \gamma_{X}: H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}_{\mathbb C} \xrightarrow{\sim} H^{1}(X, \mathcal O)\otimes_{\mathbb Z} \mathbb C \end{align*} $$
with respect to the integral structures provided by
![]() $H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}$
and the abelian group underlying
$H^{1}_{B}(X_{\mathbb C}, \mathbb Z(1))^{+}$
and the abelian group underlying
![]() $H^{1}(X, \mathcal O)$
.
$H^{1}(X, \mathcal O)$
.
Proof. We can start with the left-hand side and rewrite it as follows:
 $$ \begin{align*} \begin{aligned} &\frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1)}{\zeta^{*}(X,1)} \nonumber \\[3pt] &\quad \overset{}{=} \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1)}{\chi(X,1)} = \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1) \cdot\chi_{B}(X,1)}{\chi_{A}(X,1) \cdot \chi_{A^{\prime}}(X,1)\cdot \chi(C(1))}\\[3pt] &\quad = \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1) \cdot\chi(\gamma_{X})}{1\cdot \frac{1}{w}\cdot \chi(C(1)) \cdot \frac{{(2\pi)}^{r_{2}}}{\sqrt{|d_{F}|}}} \quad \textrm{by}~(24), (25), (19) \\[3pt] &\quad {=} \frac{\chi(\gamma_{X}) \cdot \zeta^{*}(S,0)\cdot \zeta^{*}(S,1) \cdot w^{2} \cdot \delta^{2}\cdot \Delta_{ar}(\textrm{Pic}^{0}(X))\cdot [\textrm{Br}(X)] \cdot \sqrt{|d_{F}|}}{R^{2}\cdot (2\pi)^{r_{2}} } \quad \textrm{by}~(53)\\[3pt] &\quad = \chi(\gamma_{X}) \cdot \delta^{2}\cdot h^{2}\cdot \Delta_{ar}(\textrm{Pic}^{0}(X))\cdot [\textrm{Br}(X)] \cdot 2^{r_{1}} \quad \textrm{by}~(15), (13) \\[3pt] &\quad {=} \chi(\gamma_{X}) \cdot \delta^{2}\cdot \Delta_{ar}\left(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)} \right)\cdot [\textrm{Br}(X)] \quad \textrm{by}~(60). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1)}{\zeta^{*}(X,1)} \nonumber \\[3pt] &\quad \overset{}{=} \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1)}{\chi(X,1)} = \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1) \cdot\chi_{B}(X,1)}{\chi_{A}(X,1) \cdot \chi_{A^{\prime}}(X,1)\cdot \chi(C(1))}\\[3pt] &\quad = \frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S,1) \cdot\chi(\gamma_{X})}{1\cdot \frac{1}{w}\cdot \chi(C(1)) \cdot \frac{{(2\pi)}^{r_{2}}}{\sqrt{|d_{F}|}}} \quad \textrm{by}~(24), (25), (19) \\[3pt] &\quad {=} \frac{\chi(\gamma_{X}) \cdot \zeta^{*}(S,0)\cdot \zeta^{*}(S,1) \cdot w^{2} \cdot \delta^{2}\cdot \Delta_{ar}(\textrm{Pic}^{0}(X))\cdot [\textrm{Br}(X)] \cdot \sqrt{|d_{F}|}}{R^{2}\cdot (2\pi)^{r_{2}} } \quad \textrm{by}~(53)\\[3pt] &\quad = \chi(\gamma_{X}) \cdot \delta^{2}\cdot h^{2}\cdot \Delta_{ar}(\textrm{Pic}^{0}(X))\cdot [\textrm{Br}(X)] \cdot 2^{r_{1}} \quad \textrm{by}~(15), (13) \\[3pt] &\quad {=} \chi(\gamma_{X}) \cdot \delta^{2}\cdot \Delta_{ar}\left(\frac{\textrm{Pic}^{0}(X)}{\textrm{Pic}(S)} \right)\cdot [\textrm{Br}(X)] \quad \textrm{by}~(60). \end{aligned} \end{align*} $$
This proves the stated equivalence.
Remark 45 (T. Suzuki)
The identity (67) is an analogue for arithmetic surfaces of the Artin–Tate conjecture [Reference Tate36, Conjecture C]. Let us show this by rewriting the Artin–Tate conjecture for function fields [Reference Lichtenbaum, Ramachandran and Suzuki28, Conjecture 2]; we shall use the notation of [Reference Lichtenbaum, Ramachandran and Suzuki28] from now on.
So now let S be a smooth proper curve over a finite field
![]() $F_{q}$
, and let X be a smooth proper surface with a flat proper morphism
$F_{q}$
, and let X be a smooth proper surface with a flat proper morphism
![]() $\pi :X \to S$
whose generic fibre is a smooth geometrically connected curve
$\pi :X \to S$
whose generic fibre is a smooth geometrically connected curve
![]() $X_{0}$
over Spec
$X_{0}$
over Spec
![]() $\mathbb F_{q}(S)$
. By combining (2), (12) and (13) of [Reference Lichtenbaum, Ramachandran and Suzuki28], we obtain
$\mathbb F_{q}(S)$
. By combining (2), (12) and (13) of [Reference Lichtenbaum, Ramachandran and Suzuki28], we obtain
 $$ \begin{align*}\frac{\zeta(S,1-s) \cdot \zeta(S, s)}{\zeta(X,{s})} = \frac{P_{2}(X, q^{-s})}{P_{1}(B, q^{-s}) P_{1}(B, q^{1-s}) (1 - q^{1-s})^{2}}.\end{align*} $$
$$ \begin{align*}\frac{\zeta(S,1-s) \cdot \zeta(S, s)}{\zeta(X,{s})} = \frac{P_{2}(X, q^{-s})}{P_{1}(B, q^{-s}) P_{1}(B, q^{1-s}) (1 - q^{1-s})^{2}}.\end{align*} $$
Hence, the Artin–Tate conjecture [Reference Lichtenbaum, Ramachandran and Suzuki28, Conjecture 2] is equivalent to the identity
 $$ \begin{align*}\frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S, 1)}{\zeta^{*}(X,1} = \frac{P_{2}^{*}(X, \frac{1}{q}) \cdot q^{\mathrm{dim}~B}}{ [B(\mathbb F_{q})]^{2}\cdot (\log q)^{2}} = \frac{[\textrm{Br}(X)]\cdot \Delta_{ar}(NS(X))\cdot q^{\chi(S, R^{1}\pi_{*}{\mathcal O}_{X})}}{ [B(\mathbb F_{q})]^{2} \cdot (\log q)^{2}} \end{align*} $$
$$ \begin{align*}\frac{\zeta^{*}(S,0)\cdot \zeta^{*}(S, 1)}{\zeta^{*}(X,1} = \frac{P_{2}^{*}(X, \frac{1}{q}) \cdot q^{\mathrm{dim}~B}}{ [B(\mathbb F_{q})]^{2}\cdot (\log q)^{2}} = \frac{[\textrm{Br}(X)]\cdot \Delta_{ar}(NS(X))\cdot q^{\chi(S, R^{1}\pi_{*}{\mathcal O}_{X})}}{ [B(\mathbb F_{q})]^{2} \cdot (\log q)^{2}} \end{align*} $$
by (14), (3) and (4) of [Reference Lichtenbaum, Ramachandran and Suzuki28]. On the other hand, by [Reference Lichtenbaum, Ramachandran and Suzuki28, Proposition 13 and Corollary 5 (ii)], we have
 $$ \begin{align*}\frac{\Delta_{ar}(NS(X))}{(\log q)^{2}} = \Delta_{ar}\left(\frac{NS(X)_{0}}{\pi^{*}NS(S)}\right) \cdot \delta^{2} = [B(\mathbb F_{q})]^{2}\cdot \Delta_{ar} \left(\frac{\textrm{Pic}(X)_{0}}{\pi^{*}\textrm{Pic}(S)}\right) \cdot \delta^{2}.\end{align*} $$
$$ \begin{align*}\frac{\Delta_{ar}(NS(X))}{(\log q)^{2}} = \Delta_{ar}\left(\frac{NS(X)_{0}}{\pi^{*}NS(S)}\right) \cdot \delta^{2} = [B(\mathbb F_{q})]^{2}\cdot \Delta_{ar} \left(\frac{\textrm{Pic}(X)_{0}}{\pi^{*}\textrm{Pic}(S)}\right) \cdot \delta^{2}.\end{align*} $$
Thus, the Artin–Tate conjecture for X is equivalent to the identity
 $$ \begin{align*}\frac{\zeta^{*}(S,0) \cdot \zeta^{*}(S,1)}{\zeta^{*}(X,1)} = q^{\chi(S, R^{1}\pi_{*}{\mathcal O}_{X})}\cdot [\textrm{Br}(X)]\cdot \delta^{2}\cdot \Delta_{ar}\left(\frac{\textrm{Pic}(X)_{0}}{\pi^{*}\textrm{Pic}(S)}\right). \end{align*} $$
$$ \begin{align*}\frac{\zeta^{*}(S,0) \cdot \zeta^{*}(S,1)}{\zeta^{*}(X,1)} = q^{\chi(S, R^{1}\pi_{*}{\mathcal O}_{X})}\cdot [\textrm{Br}(X)]\cdot \delta^{2}\cdot \Delta_{ar}\left(\frac{\textrm{Pic}(X)_{0}}{\pi^{*}\textrm{Pic}(S)}\right). \end{align*} $$
The factor
 $q^{\chi (S, R^{1}\pi _{*}{\mathcal O}_{X})}$
plays the role of
$q^{\chi (S, R^{1}\pi _{*}{\mathcal O}_{X})}$
plays the role of
![]() $\chi (\gamma _{X})$
in (67).
$\chi (\gamma _{X})$
in (67).
Acknowledgements
This work was initiated at the Hausdorff Research Institute during the 2018 Trimester on Periods; we thank the organisers of the Trimester and Hausdorff Research Institute for mathematics for their support. We also thank the organisers of the Motives in Tokyo conference in 2019. The referee deserves special thanks for a detailed report containing many suggestions for improvement. We are grateful to Takashi Suzuki for his comments and suggestions. In particular, the proof in Remark 45 is due to him.
Competing Interests
None.