Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-20T04:19:30.970Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIRATIONALITY AND GEOMETRIC UNIRATIONALITY FOR HYPERSURFACES IN POSITIVE CHARACTERISTICS

Part of: Surfaces and higher-dimensional varieties Special varieties Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  08 March 2021

Keiji Oguiso  and
Stefan Schröer Open the ORCID record for Stefan Schröer [Opens in a new window]
Keiji Oguiso
Affiliation:
Department of Mathematical Sciences, The University of Tokyo, Meguro Komaba 3-8-1, Tokyo, Japan, and National Center for Theoretical Sciences, Mathematics Division, National Taiwan University Taipei, Taiwan ([email protected])
Stefan Schröer
Affiliation:
Mathematisches Institut, Heinrich-Heine-Universität, 40204Düsseldorf, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Building on work of Segre and Kollár on cubic hypersurfaces, we construct over imperfect fields of charact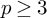eristic $p\geq 3$ particular hypersurfaces of degree p, which show that geometrically rational schemes that are regular and whose rational points are Zariski dense are not necessarily unirational. A likewise behavior holds for certain cubic surfaces in characteristic 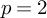$p=2$ .

Keywords

Unirationalhypersurfacesimperfect fields

MSC classification

Primary: 14M20: Rational and unirational varieties
Secondary: 14J70: Hypersurfaces 14G05: Rational points 14J26: Rational and ruled surfaces 14G17: Positive characteristic ground fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1831 - 1847
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benoist, O. and Wittenberg, O., Intermediate Jacobians and rationality over arbitrary fields, Preprint, arXiv:1909.12668.Google Scholar
Bourbaki, N., Algèbre commutative. (Hermann, Paris, 1965).Google Scholar
Colliot-Thélène, J.-L., Sansuc, J.-J. and Swinnerton-Dyer, P., Intersections of two quadrics and Châtelet surfaces, J. Reine Angew. Math. 373 (1987), 37–107.Google Scholar
Dolgachev, I., Classical Algebraic Geometry (Cambridge University Press, Cambridge, 2012).CrossRefGoogle Scholar
Fanelli, A. and Schröer, S., Del Pezzo surfaces and Mori fiber spaces in positive characteristic, Trans. Amer. Math. Soc. 373 (2020), 1775–1843.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique II: Étude globale élémentaire de quelques classes de morphismes, Publ. Math. Inst. Hautes Étud. Sci. 8 (1961), 5–222.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique IV: Étude locale des schémas et des morphismes de schémas, Publ. Math. Inst. Hautes Étud. Sci. 20 (1964), 5–259.CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique IV: Étude locale des schémas et des morphismes de schémas, Publ. Math. Inst. Hautes Étud. Sci. 24 (1965), 5–231.Google Scholar
Jouanolou, J.-P., Théorèmes de Bertini et applications, Prog. Math. Vol. 42 (Birkhäuser, Boston, 1983).Google Scholar
Kollár, J., Rational Curves on Algebraic Varieties (Springer, Berlin, 1995).Google Scholar
Kollár, J., Unirationality of cubic hypersurfaces, J. Inst. Math. Jussieu 1 (2002), 467–476.Google Scholar
Kollár, J., Smith, K. and Corti, A., Rational and Nearly Rational Varieties (Cambridge University Press, Cambridge, 2004).Google Scholar
MacLane, S., Modular fields. I. Separating transcendence bases, Duke Math. J. 5 (1939), 372–393.Google Scholar
Manin, Y., Cubic Forms. Algebra, Geometry, Arithmetic, 2nd ed. (North-Holland Publishing, Amsterdam, 1986).Google Scholar
Matsumura, H., Commutative Algebra, 2nd ed. (Benjamin/Cummings, Reading, MA, 1980).Google Scholar
Matsumura, H., Commutative Ring Theory (Cambridge University Press, Cambridge, 1986).Google Scholar
Schröer, S., On fibrations whose geometric fibers are nonreduced, Nagoya Math. J. 200 (2010), 35–57.Google Scholar
Segre, B., A note on arithmetical properties of cubic surfaces, J. London Math. Soc. 18 (1943), 24–31.CrossRefGoogle Scholar
Teichmüller, O., $p$ -Algebren, Deutsche Math. 1 (1936), 362–388.Google Scholar
van der Waerden, B., Algebra I (Springer, Berlin, 1993).Google Scholar