Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T04:55:38.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological flatness of local models for ramified unitary groups. II. The even dimensional case

Part of: Arithmetic problems. Diophantine geometry Algebraic combinatorics

Published online by Cambridge University Press:  10 July 2013

Brian D. Smithling
Brian D. Smithling*
Affiliation:
Johns Hopkins University, Department of Mathematics, 3400 N. Charles St., Baltimore, MD 21218, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Local models are schemes, defined in terms of linear-algebraic moduli problems, which are used to model the étale-local structure of integral models of certain 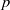$p$-adic PEL Shimura varieties defined by Rapoport and Zink. In the case of a unitary similitude group whose localization at 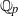${ \mathbb{Q} }_{p} $ is ramified, quasi-split 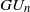$G{U}_{n} $, Pappas has observed that the original local models are typically not flat, and he and Rapoport have introduced new conditions to the original moduli problem which they conjecture to yield a flat scheme. In a previous paper, we proved that their new local models are topologically flat when $n$ is odd. In the present paper, we prove topological flatness when $n$ is even. Along the way, we characterize the 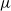$\mu $-admissible set for certain cocharacters 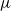$\mu $ in types 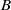$B$ and 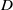$D$, and we show that for these cocharacters admissibility can be characterized in a vertexwise way, confirming a conjecture of Pappas and Rapoport.

Keywords

local modelShimura varietyunitary groupIwahori–Weyl groupadmissible set

MSC classification

Secondary: 14G35: Modular and Shimura varieties 05E15: Combinatorial aspects of groups and algebras
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 2 , April 2014 , pp. 303 - 393
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Borovoi, M., Abelian Galois cohomology of reductive groups, Mem. Amer. Math. Soc. 132 (626) (1998), viii+50 pp.Google Scholar
Bourbaki, N., Lie groups and Lie algebras (transl. from the 1968 French original by Andrew Pressley), Elements of Mathematics (Berlin) (Springer-Verlag, Berlin, 2002), Chapters 4–6.Google Scholar
Görtz, U., On the flatness of models of certain Shimura varieties of PEL-type, Math. Ann. 321 (3) (2001), 689–727.Google Scholar
Görtz, U., On the flatness of local models for the symplectic group, Adv. Math. 176 (1) (2003), 89–115.Google Scholar
Görtz, U., Topological flatness of local models in the ramified case, Math. Z. 250 (4) (2005), 775–790.CrossRefGoogle Scholar
Haines, T. J. and Ngô, B. C., Alcoves associated to special fibers of local models, Amer. J. Math. 124 (6) (2002), 1125–1152.Google Scholar
Haines, T. and Rapoport, M., On parahoric subgroups, appendix to [15].Google Scholar
Kisin, M., Integral models for Shimura varieties of abelian type, J. Amer. Math. Soc. 23 (2010), 967–1012.Google Scholar
Kottwitz, R. E., Points on some Shimura varieties over finite fields, J. Amer. Math. Soc. 5 (2) (1992), 373–444.Google Scholar
Kottwitz, R. E., Isocrystals with additional structure. II, Compos. Math. 109 (3) (1997), 255–339.Google Scholar
Kottwitz, R. and Rapoport, M., Minuscule alcoves for ${\mathrm{GL} }_{n} $ and ${\mathrm{GSp} }_{2n} $ , Manuscripta Math. 102 (4) (2000), 403–428.Google Scholar
Pappas, G., On the arithmetic moduli schemes of PEL Shimura varieties, J. Algebraic Geom. 9 (3) (2000), 577–605.Google Scholar
Pappas, G. and Rapoport, M., Local models in the ramified case. I. The EL-case, J. Algebraic Geom. 12 (1) (2003), 107–145.Google Scholar
Pappas, G. and Rapoport, M., Local models in the ramified case. II. Splitting models, Duke Math. J. 127 (2) (2005), 193–250.Google Scholar
Pappas, G. and Rapoport, M., Twisted loop groups and their affine flag varieties (with an appendix by T. Haines and Rapoport), Adv. Math. 219 (1) (2008), 118–198.Google Scholar
Pappas, G. and Rapoport, M., Local models in the ramified case. III. Unitary groups, J. Inst. Math. Jussieu 8 (3) (2009), 507–564.Google Scholar
Pappas, G., Rapoport, M. and Smithling, B., Local models of Shimura varieties, I. Geometry and combinatorics, in Handbook of Moduli, Volume III (ed. Farkas, G. and Morrison, I.), Advanced Lectures in Mathematics, Volume 26, pp. 135–217 (International Press, Somerville, MA, USA, 2013).Google Scholar
Pappas, G. and Zhu, X., Local models of Shimura varieties and a conjecture of Kottwitz, Invent. Math., in press.Google Scholar
Rapoport, M., A guide to the reduction modulo p of Shimura varieties, Automorphic forms. I (English, with English and French summaries), Astérisque 298 (2005), 271–318.Google Scholar
Rapoport, M. and Zink, Th., Period spaces for p-divisible groups, Annals of Mathematics Studies, Volume 141 (Princeton University Press, Princeton, NJ, USA, 1996).Google Scholar
Richarz, T., Schubert varieties in twisted affine flag varieties and local models, J. Algebra 375 (2013), 121–147.Google Scholar
Smithling, B. D., Topological flatness of orthogonal local models in the split, even case. I, Math. Ann. 350 (2) (2011), 381–416.Google Scholar
Smithling, B. D., Admissibility and permissibility for minuscule cocharacters in orthogonal groups, Manuscripta Math. 136 (3–4) (2011), 295–314.Google Scholar
Smithling, B. D., Topological flatness of local models for ramified unitary groups. I. The odd dimensional case, Adv. Math. 226 (4) (2011), 3160–3190.Google Scholar
Steinberg, R., Endomorphisms of linear algebraic groups, Memoirs of the American Mathematical Society, Volume 80 (American Mathematical Society, Providence, RI, USA, 1968).Google Scholar
Tits, J., Reductive groups over local fields, in Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proc. Sympos. Pure Math., Volume XXXIII, pp. 29–69 (Amer. Math. Soc., Providence, RI, USA, 1979).Google Scholar
Vasiu, A., Geometry of Shimura varieties of Hodge type over finite fields, in Higher-dimensional geometry over finite fields, NATO Sci. Peace Secur. Ser. D Inf. Commun. Secur., Volume 16, pp. 197–243 (IOS, Amsterdam, 2008).Google Scholar
Zhu, X., On the coherence conjecture of Pappas and Rapoport, Ann. of Math., in press.Google Scholar