Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T16:20:08.027Z Has data issue: false hasContentIssue false
  • English
  • Français

SHIFTED COISOTROPIC CORRESPONDENCES

Part of: Categories with structure Algebraic geometry: Foundations Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  03 July 2020

Rune Haugseng ,
Valerio Melani Open the ORCID record for Valerio Melani [Opens in a new window]  and
Pavel Safronov
Rune Haugseng
Affiliation:
Norwegian University of Science and Technology (NTNU), Trondheim, Norway ([email protected]) URL: folk.ntnu.no/runegha
Valerio Melani
Affiliation:
Dipartimento di Matematica, Università di Pisa, Pisa, Italy ([email protected])
Pavel Safronov
Affiliation:
Institut für Mathematik, Universität Zürich, Zurich, Switzerland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We define (iterated) coisotropic correspondences between derived Poisson stacks, and construct symmetric monoidal higher categories of derived Poisson stacks, where the $i$-morphisms are given by $i$-fold coisotropic correspondences. Assuming an expected equivalence of different models of higher Morita categories, we prove that all derived Poisson stacks are fully dualizable and so determine framed extended TQFTs by the Cobordism Hypothesis. Along the way, we also prove that the higher Morita category of 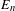$E_{n}$-algebras with respect to coproducts is equivalent to the higher category of iterated cospans.

Keywords

derived algebraic geometryhigher categoriescoisotropic structures

MSC classification

Primary: 14A20: Generalizations (algebraic spaces, stacks)
Secondary: 17B63: Poisson algebras 18D05: Double categories, $2$-categories, bicategories and generalizations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 785 - 849
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work of P.S. was supported by the NCCR SwissMAP grant of the Swiss National Science Foundation. R.H. received funding from grant IBS-R003-D1 of the Institute for Basic Science of the Republic of Korea.

References

Baranovsky, V. and Ginzburg, V., Gerstenhaber–Batalin–Vilkovisky structures on coisotropic intersections, Math. Res. Lett. 17(2) (2010), 211–229.CrossRefGoogle Scholar
Barwick, C., ‘ $(\infty ,n)$ -Cat as a closed model category’, PhD thesis, University of Pennsylvania (2005).Google Scholar
Barwick, C. and Glasman, S., ‘On the fibrewise effective Burnside category’, (2016),arXiv:1607.02786.Google Scholar
Barwick, C. and Schommer-Pries, C., ‘On the unicity of the homotopy theory of higher categories’, (2011), arXiv:1112.0040.Google Scholar
Behrend, K. and Fantechi, B., Gerstenhaber and Batalin–Vilkovisky structures on Lagrangian intersections, in Algebra, Arithmetic, and Geometry: in honor of Yu. I. Manin. Vol. I, Progress in Mathematics, vol. 269, pp. 1–47 (Birkhäuser Boston Inc., Boston, MA, 2009).Google Scholar
Calaque, D., Haugseng, R. and Scheimbauer, C., ‘The AKSZ construction in derived algebraic geometry as an extended topological quantum field theory’, (2020) In preparation.Google Scholar
Calaque, D., Pantev, T., Toën, B., Vaquié, M. and Vezzosi, G., Shifted Poisson structures and deformation quantization, J. Topol. 10(2) (2017), 483–584.CrossRefGoogle Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry. Vol. I. Correspondences and duality, Mathematical Surveys and Monographs, vol. 221 (American Mathematical Society, Providence, RI, 2017). Available from http://www.math.harvard.edu/∼gaitsgde/GL/.Google Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry. Vol. II. Deformations, Lie theory and formal geometry, Mathematical Surveys and Monographs, vol. 221 (American Mathematical Society, Providence, RI, 2017). Available from http://www.math.harvard.edu/∼gaitsgde/GL/.Google Scholar
Gepner, D. and Haugseng, R., Enriched ∞-categories via non-symmetric ∞-operads, Adv. Math. 279 (2015), 575–716.CrossRefGoogle Scholar
Gepner, D., Haugseng, R. and Nikolaus, T., Lax colimits and free fibrations in ∞-categories, Doc. Math. 22 (2017), 1225–1266.Google Scholar
Gwilliam, O. and Haugseng, R., Linear Batalin–Vilkovisky quantization as a functor of ∞-categories, Selecta Math. 24(2) (2018), 1247–1313.CrossRefGoogle Scholar
Gwilliam, O. and Scheimbauer, C., ‘Duals and adjoints in higher Morita categories’, (2018), arXiv:1804.10924.Google Scholar
Haugseng, R., Iterated spans and classical topological field theories, Math. Z. 289(3) (2018), 1427–1488.CrossRefGoogle Scholar
Haugseng, R., The higher Morita category of E n-algebras, Geom. Topol. 21 (2017), 1631–1730.CrossRefGoogle Scholar
Johnson-Freyd, T., Poisson AKSZ theories and their quantizations, in String-Math 2013, Proceedings of Symposia in Pure Mathematics, vol. 88, pp. 291–306 (American Mathematical Society, Providence, RI, 2014).CrossRefGoogle Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009). Available from http://math.harvard.edu/∼lurie/.CrossRefGoogle Scholar
Lurie, J., On the classification of topological field theories, in Current Developments in Mathematics, 2008, pp. 129–280 (Int. Press, Somerville, MA, 2009). Available at http://math.harvard.edu/∼lurie/papers/cobordism.pdf.Google Scholar
Lurie, J., ‘Derived algebraic geometry X: formal moduli problems’, (2011), available at http://math.harvard.edu/∼lurie/papers/DAG-X.pdf.Google Scholar
Lurie, J., ‘Higher Algebra’, (2017), available at http://math.harvard.edu/∼lurie/.Google Scholar
Lurie, J., ‘Spectral algebraic geometry’, (2018), available at http://math.harvard.edu/∼lurie/.Google Scholar
Melani, V., Poisson bivectors and Poisson brackets on affine derived stacks, Adv. Math. 288(4) (2016), 1097–1120.CrossRefGoogle Scholar
Melani, V. and Safronov, P., Derived coisotropic structures I: affine case, Selecta Math. 24(4) (2018), 3061–3118.CrossRefGoogle Scholar
Melani, V. and Safronov, P., Derived coisotropic structures II: stacks and quantization, Selecta Math. 24(4) (2018), 3119–3173.CrossRefGoogle Scholar
Pantev, T., Toën, B., Vaquié, M. and Vezzosi, G., Shifted symplectic structures, Publ. Math. Inst. Hautes Études Sci. 117 (2013), 271–328.CrossRefGoogle Scholar
Pantev, T. and Vezzosi, G., Symplectic and Poisson derived geometry and deformation quantization, in Algebraic Geometry 2015 – Proceedings of the AMS Summer Institute, Proceedings of Symposia in Pure Mathematics, vol. 97, (Amer. Math. Society, Providence, RI, USA, 2018).Google Scholar
Pridham, J. P., Shifted Poisson and symplectic structures on derived N-stacks, J. Topol. 10(1) (2017), 178–210.CrossRefGoogle Scholar
Pridham, J. P., ‘Quantisation of derived Lagrangians’, (2016), available at arXiv:1607.01000.Google Scholar
Rezk, C., A model for the homotopy theory of homotopy theory, Trans. Amer. Math. Soc. 353(3) (2001), 973–1007 (electronic).CrossRefGoogle Scholar
Riehl, E. and Verity, D., Homotopy coherent adjunctions and the formal theory of monads, Adv. Math. 286 (2016), 802–888.Google Scholar
Safronov, P., Poisson reduction as a coisotropic intersection, Higher Struct. 1(1) (2017), 87–121.Google Scholar
Safronov, P., Braces and Poisson additivity, Compos. Math. 154(8) (2018), 1698–1745.CrossRefGoogle Scholar
Scheimbauer, C., ‘Factorization homology as a fully extended topological field theory’, PhD thesis, Eidgenössische Technische Hochschule, Zürich, (2014), available at http://guests.mpim-bonn.mpg.de/scheimbauer/.Google Scholar
Toën, B. and Vezzosi, G., Homotopical algebraic geometry II: geometric stacks and applications, Mem. Amer. Math. Soc. 193(902) (2008), available at arXiv:math/0404373.Google Scholar
Wehrheim, K. and Woodward, C. T., Functoriality for Lagrangian correspondences in Floer theory, Quant. Topol. 1(2) (2010), 129–170.Google Scholar
Weinstein, A., Coisotropic calculus and Poisson groupoids, J. Math. Soc. Japan 40(4) (1988), 705–727.Google Scholar
Weinstein, A., The symplectic ‘category’, in Differential Geometric Methods in Mathematical Physics (Clausthal, 1980), Lecture Notes in Mathematics, vol. 905, pp. 45–51 (Springer, Berlin-New York, 1982).CrossRefGoogle Scholar
Weinstein, A., Symplectic categories, Port. Math. 67(2) (2010), 261–278.CrossRefGoogle Scholar