Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T10:06:04.641Z Has data issue: false hasContentIssue false
  • English
  • Français

SEMIABELIAN VARIETIES OVER SEPARABLY CLOSED FIELDS, MAXIMAL DIVISIBLE SUBGROUPS, AND EXACT SEQUENCES

Published online by Cambridge University Press:  17 July 2014

Franck Benoist ,
Elisabeth Bouscaren  and
Anand Pillay
Franck Benoist
Affiliation:
Department of Mathematics, Univ. Paris-Sud, Bat. 425, F-91405 Orsay Cedex, France ([email protected])
Elisabeth Bouscaren
Affiliation:
Department of Mathematics, CNRS - Univ. Paris-Sud, Bat. 425, F-91405 Orsay Cedex, France ([email protected])
Anand Pillay
Affiliation:
Department of Mathematics, University of Notre Dame, 281 Hurley Hall, Notre Dame, IN 46556, USA ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a separably closed field 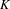$K$ of characteristic 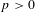$p>0$ and finite degree of imperfection, we study the 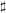$\sharp$ functor which takes a semiabelian variety 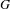$G$ over 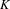$K$ to the maximal divisible subgroup of 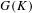$G(K)$. Our main result is an example where 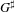$G^{\sharp }$, as a ‘type-definable group’ in 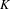$K$, does not have ‘relative Morley rank’, yielding a counterexample to a claim in Hrushovski [J. Amer. Math. Soc. 9 (1996), 667–690]. Our methods involve studying the question of the preservation of exact sequences by the 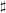$\sharp$ functor, and relating this to issues of descent as well as model-theoretic properties of 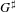$G^{\sharp }$. We mention some characteristic 0 analogues of these ‘exactness-descent’ results, where differential algebraic methods are more prominent. We also develop the notion of an iterative D-structure on a group scheme over an iterative Hasse field, which is interesting in its own right, as well as providing a uniform treatment of the characteristic 0 and characteristic 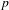$p$ cases of ‘exactness descent’.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 1 , January 2016 , pp. 29 - 69
Copyright
© Cambridge University Press 2014 

References

Benoist, F., Théorie des modèles des corps munis d’une dérivation de Hasse, PhD thesis, Univ. Paris 7 (2005).Google Scholar
Benoist, F., A theorem of the Kernel in characteristic $p$, preprint, 2011.Google Scholar
Benoist, F., Schemes with D-structure, preprint, 2014, http://www.math.u-psud.fr/∼fbenoist/Dstructure.pdf.Google Scholar
Benoist, F. and Delon, F. , Questions de corps de définition pour les variétés abéliennes en caractéristique positive, Journal de l’Institut de Mathématiques de Jussieu 7 (2008), 623–639.Google Scholar
Bertrand, D., Endomorphismes de groupes algébriques, in Diophantine Approximations and Transcendental Numbers (Luminy, 1982).Google Scholar
Bertrand, D. and Pillay, A., A Lindemann–Weierstrass theorem for semiabelian varieties over function fields, J. Amer. Math. Soc. 23 (2010), 491–533.Google Scholar
Bouscaren, E. and Delon, F., Groups definable in separably closed fields, Trans. Amer. Math. Soc. 354 (2002), 945–966.Google Scholar
Bouscaren, E. and Delon, F., Minimal groups in separably closed fields, J. Symbolic Logic 67 (2002), 239–259.CrossRefGoogle Scholar
Borel, A., Linear algebraic groups, 2nd enlarged ed., Graduate Text in Mathematics, (Springer, New York, 1991).Google Scholar
Buium, A., Differential algebraic group of finite dimension, Lecture Notes in Mathematics 1506 (Springer-Verlag, 1992).Google Scholar
Buium, A., Differential Algebra and Diophantine Geometry (Hermann, Paris, 1994).Google Scholar
Conrad, B., Chow’s K∕k-image and K∕k-trace and the Lang–Néron theorem, Enseign. Math. (2) 52 (2006), 37–108.Google Scholar
Demazure, M. and Gabriel, P., Groupes algébriques Tome I (Masson, Paris, 1970).Google Scholar
Erimbetov, M. M., Complete theories with 1-cardinal formulas, Algebra Logika 14 (1975), 245–257.CrossRefGoogle Scholar
Grothendieck, A. and Raynaud, M., Revêtements étales et groupe fondamental, in Séminaire de géométrie algébrique du Bois Marie (SGA1), 1960–61, Lecture Notes in Mathematics, Volume 224 (Springer-Verlag, 1971).Google Scholar
Hrushovski, E., The Mordell–Lang conjecture for function fields, J. Amer. Math. Soc. 9 (1996), 667–690.Google Scholar
Kowalski, P. and Pillay, A. , Quantifier elimination for algebraic D-groups, Trans. Amer. Math. Soc. 358 (2006), 167–181.Google Scholar
Kowalski, P. and Pillay, A. , On the isotriviality of projective iterative ∂-varieties, J. Pure Appl. Algebra 216 (2012), 20–37.Google Scholar
Lang, S., Abelian Varieties (Interscience, London, 1959).Google Scholar
Marker, D., Manin kernels, Quaderni Math., Volume 6, pp. 1–21 (Napoli, 2000).Google Scholar
Marker, D., Model theory of differential fields, in Model Theory of Fields, second edition, Lecture Notes in Logic (ASL, AK Peters, 2006).Google Scholar
Marker, D. and Pillay, A., Differential Galois Theory III: Some inverse problems, Illinois J. Math. 41 (1997), 453–461.Google Scholar
Mazur, B. and Messing, W., Universal extensions and one dimensional crystalline cohomology, Lecture Notes in Mathematics, Volume 370 (Springer, 1974).Google Scholar
Milne, J. S., Etale cohomology (Princeton University Press, 1980).Google Scholar
Moosa, R. and Scanlon, T. , Jet and prolongations spaces, J. Inst. Math. Jussieu 9 (2010), 391–430.Google Scholar
Mumford, D., Abelian varieties (Oxford University Press, 1985). Published for the Tata Institute of Fundamental Research, Bombay.Google Scholar
Mumford, D. and Fogarty, J., Geometric invariant theory, 2nd enlarged edition (Springer, 1982).CrossRefGoogle Scholar
Pillay, A., Differential algebraic groups and the number of countable differentially closed fields, in Model Theory of Fields, cited above.Google Scholar
Poizat, B., Stable groups, Mathematical Surveys and Monographs (American Mathematical Society, 2001).Google Scholar
Rosenlicht, M., Some basic theorems on algebraic groups, Amer. J. Math. 76 (1956), 401–443.Google Scholar
Rosenlicht, M., Extensions of vector groups by abelian varieties, Amer. J. Math. 80 (1958), 685–714.Google Scholar
Rössler, D., Infinitely p-divisible points on abelian varieties defined over function fields of characteristic p > 0, Notre Dame J. Formal Logic 54 (2013), 579–589.CrossRefGoogle Scholar
Serre, J.-P., Quelques propriétes des variétes abéliennes en caractéristique p, Amer. J. Math. 80(3) (1958), 715–739.Google Scholar
Serre, J.-P., Algebraic groups and class fields, Graduate Texts in Mathematics (Springer, 1988).Google Scholar
Shelah, S., Classification Theory, 2nd ed. (North Holland, 1990).Google Scholar
Silverman, J. H., The arithmetic of elliptic curves, Graduate Texts in Mathematics (Springer-Verlag, 1986).Google Scholar
Vojta, P., Jets via Hasse–Schmidt derivations, in Diophantine Geometry, CRM Series, Volume 4, pp. 335–361 (Ed. Norm., Pisa, 2007).Google Scholar
Voloch, F., Diophantine approximation on Abelian varieties in characteristic p, Amer. J. Math. 4 (1995), 1089–1095.Google Scholar
Wagner, F. O., Stable groups, London Mathematical Society Lecture Notes (Cambridge University Press, 1997).CrossRefGoogle Scholar
Ziegler, M., A remark on Morley rank, preprint 1997, http://home.mathematik.uni-freiburg.de/ziegler/Preprints.html.Google Scholar
Ziegler, M., Separably closed fields with Hasse derivations, J. Symbolic Logic 68 (2003), 311–318.CrossRefGoogle Scholar