Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T09:53:05.407Z Has data issue: false hasContentIssue false
  • English
  • Français

RIGIDITY FOR RIGID ANALYTIC MOTIVES

Part of: Arithmetic problems. Diophantine geometry Cycles and subschemes $K$-theory in number theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  27 September 2019

Federico Bambozzi  and
Alberto Vezzani Open the ORCID record for Alberto Vezzani [Opens in a new window]
Federico Bambozzi
Affiliation:
Mathematical Institute - University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK ([email protected])
Alberto Vezzani
Affiliation:
LAGA - Université Paris 13, Sorbonne Paris Cité, 99 av. Jean-Baptiste Clément, 93430Villetaneuse, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove the Rigidity Theorem for motives of rigid analytic varieties over a non-Archimedean valued field 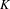$K$. We prove this theorem both for motives with transfers and without transfers in a relative setting. Applications include the construction of étale realization functors, an upgrade of the known comparison between motives with and without transfers and an upgrade of the rigid analytic motivic tilting equivalence, extending them to 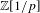$\mathbb{Z}[1/p]$-coefficients.

Keywords

Rigidity Theoremrigid analytic varietiesmotivestilting equivalence

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives 14G22: Rigid analytic geometry
Secondary: 11G25: Varieties over finite and local fields 19F27: Étale cohomology, higher regulators, zeta and $L$-functions
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 4 , July 2021 , pp. 1341 - 1369
Check for updates
Copyright
© The Author(s), 2019. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author acknowledges the University of Regensburg with the support of the DFG funded CRC 1085 ‘Higher Invariants. Interactions between Arithmetic Geometry and Global Analysis’. The second author was partially supported by the ANR Grant PERCOLATOR: ANR-14-CE25-0002-01 and by the ANR JCJC Grant PERGAMO: ANR-18-CE40-0017.

References

Adiprasito, K., Liu, G., Pak, I. and Temkin, M., Log smoothness and polystability over valuation rings, preprint, 2018, arXiv:1806.09168 [math.AG].Google Scholar
Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique, I, Astérisque 314 (2008), x+466 pp, 2007.Google Scholar
Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique, II, Astérisque 315 (2008), vi+364 pp, 2007.Google Scholar
Ayoub, J., La réalisation étale et les opérations de Grothendieck, Ann. Sci. Éc. Norm. Supér. (4) 47(1) (2014), 1–145.CrossRefGoogle Scholar
Ayoub, J., Note sur les opérations de Grothendieck et la réalisation de Betti, J. Inst. Math. Jussieu 9(2) (2010), 225–263.CrossRefGoogle Scholar
Ayoub, J., Motifs des variétés analytiques rigides, Mém. Soc. Math. Fr. (N.S.) 140–141 (2015), vi+386 pp.Google Scholar
Berkovich, V. G., Smooth p-adic analytic spaces are locally contractible, Invent. Math. 137(1) (1999), 1–84.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., The pro-étale topology for schemes, Astérisque 369 (2015), 99–201.Google Scholar
Binda, F. and Krishna, A., Rigidity for relative $0$ -cycles, preprint, 2018, arXiv:1802.00165 [math.AG].Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., A systematic approach to rigid analytic geometry, in Non-Archimedean Analysis, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 261 (Springer-Verlag, Berlin, 1984).CrossRefGoogle Scholar
Choudhury, U. and de Souza, M. G. A., Homotopy theory of dg sheaves, Comm. Algebra 47(8) (2019), 3202–3228.CrossRefGoogle Scholar
Cisinski, D.-C. and Déglise, F., Étale motives, Compos. Math. 152(3) (2016), 556–666.CrossRefGoogle Scholar
Dugger, D., Universal homotopy theories, Adv. Math. 164(1) (2001), 144–176.CrossRefGoogle Scholar
Fresnel, J. and van der Put, M., Rigid Analytic Geometry and its Applications, Progress in Mathematics, Volume 218 (Birkhäuser Boston, Inc., Boston, MA, 2004).CrossRefGoogle Scholar
Gabber, O., K-theory of Henselian local rings and Henselian pairs, in Algebraic K-theory, Commutative Algebra, and Algebraic Geometry (Santa Margherita Ligure, 1989), Contemporary Mathematics, Volume 126, pp. 59–70 (American Mathematical Society, Providence, RI, 1992).Google Scholar
Grothendieck, A., Éléments de géométrie algébrique IV. Étude locale des schémas et des morphismes de schémas, Publ. Math. Inst. Hautes Études Sci. 32 (1967), 361.Google Scholar
Hovey, M., Model Categories, Mathematical Surveys and Monographs, Volume 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Hovey, M., Spectra and symmetric spectra in general model categories, J. Pure Appl. Algebra 165(1) (2001), 63–127.CrossRefGoogle Scholar
Huber, R., Étale Cohomology of Rigid Analytic Varieties and Adic Spaces, Aspects of Mathematics, Volume E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).CrossRefGoogle Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture Notes on Motivic Cohomology, Clay Mathematics Monographs, Volume 2 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.CrossRefGoogle Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties, Forum Math. Pi 1(e1) (2013), 77.CrossRefGoogle Scholar
Scholze, P., Etale cohomology of diamonds, preprint, 2017, arXiv:1709.07343 [math.AG].CrossRefGoogle Scholar
Suslin, A., On the K-theory of algebraically closed fields, Invent. Math. 73(2) (1983), 241–245.CrossRefGoogle Scholar
Suslin, A., On the $K$ -theory of local fields, in Proceedings of the Luminy Conference on Algebraic $K$ -theory (Luminy, 1983), J. Pure Appl. Algebra 34(2–3) (1984), 301–318.CrossRefGoogle Scholar
Vezzani, A., Effective motives with and without transfers in characteristic p , Adv. Math. 306 (2017), 852–879.CrossRefGoogle Scholar
Vezzani, A., The Monsky–Washnitzer and the overconvergent realizations, Int. Math. Res. Not. IMRN 11 (2018), 3443–3489.CrossRefGoogle Scholar
Vezzani, A., Rigid cohomology via the tilting equivalence, J. Pure Appl. Algebra 223(2) (2019), 818–843.CrossRefGoogle Scholar
Vezzani, A., A motivic version of the theorem of Fontaine and Wintenberger, Compos. Math. 155(1) (2019), 38–88.CrossRefGoogle Scholar
Vezzani, A., The Berkovich realization for rigid analytic motives, J. Algebra 527 (2019), 30–54.CrossRefGoogle Scholar
Voevodsky, V., Suslin, A. and Friedlander, E. M., Cycles, Transfers, and Motivic Homology Theories, Annals of Mathematics Studies, Volume 143 (Princeton University Press, Princeton, NJ, 2000).Google Scholar