Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T06:54:32.890Z Has data issue: false hasContentIssue false
  • English
  • Français

RIGID ORBITS AND SHEETS IN REDUCTIVE LIE ALGEBRAS OVER FIELDS OF PRIME CHARACTERISTIC

Part of: Lie algebras and Lie superalgebras Linear algebraic groups and related topics

Published online by Cambridge University Press:  04 April 2016

Alexander Premet  and
David I. Stewart
Alexander Premet
Affiliation:
The University of Manchester, Oxford Road, M13 9PL, UK ([email protected])
David I. Stewart
Affiliation:
University of Newcastle, NE1 7RU, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 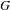$G$ be a simple simply connected algebraic group over an algebraically closed field 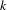$k$ of characteristic 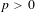$p>0$ with 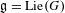$\mathfrak{g}=\text{Lie}(G)$. We discuss various properties of nilpotent orbits in 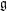$\mathfrak{g}$, which have previously only been considered over 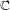$\mathbb{C}$. Using computational methods, we extend to positive characteristic various calculations of de Graaf with nilpotent orbits in exceptional Lie algebras. In particular, we classify those orbits which are reachable as well as those which satisfy a certain related condition due to Panyushev, and determine the codimension of the derived subalgebra 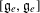$[\mathfrak{g}_{e},\mathfrak{g}_{e}]$ in the centraliser 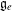$\mathfrak{g}_{e}$ of any nilpotent element 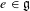$e\in \mathfrak{g}$. Some of these calculations are used to show that the list of rigid nilpotent orbits in 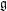$\mathfrak{g}$, the classification of sheets of 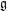$\mathfrak{g}$ and the distribution of the nilpotent orbits amongst them are independent of good characteristic, remaining the same as in the characteristic zero case. We also give a comprehensive account of the theory of sheets in reductive Lie algebras over algebraically closed fields of good characteristic.

Keywords

reductive groupdecomposition classinduced nilpotent orbit

MSC classification

Primary: 17B45: Lie algebras of linear algebraic groups 20G15: Linear algebraic groups over arbitrary fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 3 , June 2018 , pp. 583 - 613
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Borho, W. and Kraft, H., Über Bahnen und deren Deformationen bei linearen Aktionen reduktiver Gruppen, Comment. Math. Helv. 54(1) (1979), 61–104.Google Scholar
Borel, A., Linear Algebraic Groups, second edition, Graduate Texts in Mathematics, Volume 126 (Springer, New York, 1991).CrossRefGoogle Scholar
Borho, W., Über Schichten halbeinfacher Lie-Algebren, Invent. Math. 65(2) (1981/82), 283–317.Google Scholar
Bardsley, P. and Richardson, R. W., Étale slices for algebraic transformation groups in characteristic p , Proc. Lond. Math. Soc. (3) 51(2) (1985), 295–317.Google Scholar
Carter, R. W., Conjugacy classes in the Weyl group, Compos. Math. 25 (1972), 1–59.Google Scholar
Carter, R. W., Finite Groups of Lie Type: Conjugacy Classes and Complex Characters (Wiley Classics Library. John Wiley & Sons Ltd., Chichester, 1993). Reprint of the 1985 Wiley–Interscience Publication.Google Scholar
de Graaf, W. A., Computations with nilpotent orbits in SLA. Preprint, 2013.Google Scholar
de Graaf, W. A. and Elashvili, A., Induced nilpotent orbits of the simple Lie algebras of exceptional type, Georgian Math. J. 16(2) (2009), 257–278.Google Scholar
Eisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry, Graduate Texts in Mathematics, Volume 150 (Springer, New York, 1995).Google Scholar
Elashvili, A., Sheets of the exceptional Lie algebras, Stud. Algebra 171 (1984).Google Scholar
Fossum, R. M., One-dimensional formal group actions, in Invariant Theory (Denton, TX, 1986), Contemporary Mathematics, Volume 88, pp. 227–397 (American Mathematical Society, Providence, RI, 1989).Google Scholar
Hesselink, W. H., Nilpotency in classical groups over a field of characteristic 2, Math. Z. 166(2) (1979), 165–181.Google Scholar
Jantzen, J. C., Nilpotent orbits in representation theory, in Lie Theory, Progressive Mathematics, Volume 228, pp. 1–211 (Birkhäuser Boston, Boston, MA, 2004).Google Scholar
Kempken, G., Induced conjugacy classes in classical Lie algebras, Abh. Math. Sem. Univ. Hamburg 53 (1983), 53–83.Google Scholar
Kraft, H., Parametrisierung von Konjugationsklassen in sl n , Math. Ann. 234(3) (1978), 209–220.Google Scholar
Lawther, R., Jordan block sizes of unipotent elements in exceptional algebraic groups, Comm. Algebra 23(11) (1995), 4125–4156.Google Scholar
Lusztig, G. and Spaltenstein, N., Induced unipotent classes, J. Lond. Math. Soc. (2) 19(1) (1979), 41–52.Google Scholar
Lusztig, G., Character sheaves on disconnected groups, II, Represent. Theory 8 (2004), 72–124.Google Scholar
Liebeck, M. W. and Seitz, G. M., Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras, Mathematical Surveys and Monographs, Volume 180 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Lawther, R. and Testerman, D. M., Centres of centralizers of unipotent elements in simple algebraic groups, Mem. Amer. Math. Soc. 210(988) (2011), vi+188.Google Scholar
McNinch, G. J., Adjoint Jordan blocks. Preprint, 2002.Google Scholar
Mcninch, G. J., Nilpotent orbits over ground fields of good characteristic, Math. Ann. 329(1) (2004), 49–85.Google Scholar
Premet, A., Nilpotent orbits in good characteristic and the Kempf–Rousseau theory, J. Algebra 260(1) (2003), 338–366. Special issue celebrating the 80th birthday of Robert Steinberg.Google Scholar
Premet, A. and Skryabin, S., Representations of restricted Lie algebras and families of associative L-algebras, J. Reine Angew. Math. 507 (1999), 189–218.Google Scholar
Premet, A., Commutative quotients of finite W-algebras, Adv. Math. 225 (2010), 269–306.Google Scholar
Premet, A. and Topley, L., Derived subalgebras of centralisers and finite W-algebras, Compos. Math. 150(9) (2014), 1485–1548.Google Scholar
Rosenlicht, M., On quotient varieties and the affine embedding of certain homogeneous spaces, Trans. Amer. Math. Soc. 101 (1961), 211–223.Google Scholar
Spaltenstein, N., Classes Unipotentes et Sous-groupes de Borel, Lecture Notes in Mathematics, Volume 946 (Springer, Berlin–New York, 1982).CrossRefGoogle Scholar
Spaltenstein, N., Nilpotent classes and sheets of Lie algebras in bad characteristic, Math. Z. 181(1) (1982), 31–48.Google Scholar
Spaltenstein, N., Nilpotent classes in Lie algebras of type F 4 over fields of characteristic 2, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 30(3) (1984), 517–524.Google Scholar
Springer, T. A. and Steinberg, R., Conjugacy classes, in Seminar on Algebraic Groups and Related Finite Groups (The Institute for Advanced Study, Princeton, NJ, 1968/69), Lecture Notes in Mathematics, Volume 131, pp. 167–266 (Springer, Berlin, 1970).Google Scholar
University of Georgia VIGRE Algebra Group, Varieties of nilpotent elements for simple Lie algebras I: good primes, J. Algebra 280 (2004), 719–737. The University of Georgia VIGRE Algebra Group: D. J. Benson, P. Bergonio, B. D. Boe, L. Chastkofsky, D. Cooper, J. Jungster, G. M. Guy, J. J. Hyun, G. Matthews, N. Mazza, D. K. Nakano, K. J. Platt.Google Scholar
University of Georgia VIGRE Algebra Group, Varieties of nilpotent elements for simple Lie algebras: II. Bad primes, J. Algebra 292 (2005), 65–99. The University of Georgia VIGRE Algebra Group: D. J. Benson, P. Bergonio, B. D. Boe, L. Chastkofsky, B. Cooper, G. M. Guy, J. Hower, M. Hunziker, J. J. Hyun, J. Kujawa, G. Matthews, N. Mazza, D. K. Nakano, K. J. Platt and C. Wright.Google Scholar
Yakimova, O., On the derived algebra of a centraliser, Bull. Sci. Math. 134(6) (2010), 579–587.Google Scholar