Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T08:59:14.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Première classe de Stiefel–Whitney des espaces d'applications stables réelles en genre zéro vers une surface convexe

Part of: Projective and enumerative geometry (Co)homology theory Local differential geometry

Published online by Cambridge University Press:  15 December 2008

Nicolas Puignau
Nicolas Puignau
Affiliation:
Universidad Complutense Madrid, Departamento de Álgebra, Facultad de Ciencias Matemáticas, Plaza de Ciencias, 3, 28040 Madrid, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (X, cX) be a convex projective surface equipped with a real structure. The space of stable maps 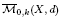carries different real structures induced by cX and any order two element τ of permutation group Sk acting on marked points. Each corresponding real part ℝτ 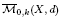is a real normal projective variety. As the singular locus is of codimension bigger than two, these spaces thus carry a first Stiefel–Whitney class for which we determine a representative in the case k = c1(X)d − 1 where c1(X) is the first Chern class of X. Namely, we give a homological description of these classes in term of the real part of boundary divisors of the space of stable maps.

Résumé

Soit (X, cX) une surface projective convexe munie d'une structure réelle. L'espace de module des applications stables 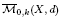peut être équipé de plusieurs structures réelles associées à cX et à un élément d'ordre deux τ du groupe des permutations Sk qui agit sur les points marqués. La partie réelle correspondant à chaque structure ℝτ 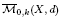est une variété réelle projective et normale. Puisque le lieu singulier est de codimension au moins deux, ces espaces possèdent une première classe de Stiefel–Whitney pour laquelle on détermine un représentant dans le cas k = c1(X)d − 1 où c1(X) désigne la première classe de Chern du fibré tangent de X. Plus précisément, nous donnons une description homologique des classes de Stiefel–Whitney en termes de partie réelle de certains diviseurs de la frontière de l'espace des applications stables.

Keywords

espace de modulescourbes rationnellesgéométrie énumérative réellemoduli spacesrational curvesreal enumerative geometry

MSC classification

Secondary: 14F25: Classical real and complex (co)homology 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 14P25: Topology of real algebraic varieties 53B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 8 , Issue 2 , April 2009 , pp. 383 - 414
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

1.Behrend, K. et Manin, Y., Stacks of stable maps and Gromov–Witten invariants, Duke Math. J. 85 (1996), 1–60.CrossRefGoogle Scholar
2.Fulton, W. et Pandharipande, R., Notes on stable maps and quantum cohomology, Proc. Symp. Pure Math. 62 (1997), 45–96.CrossRefGoogle Scholar
3.Kollár, J., Rational curves on algebraic varieties (Springer, 1996).CrossRefGoogle Scholar
4.Kontsevich, M. et Manin, Y., Gromov–Witten classes, quantum cohomology, and enumerative geometry, Commun. Math. Phys. 164(3) (1994), 525–562.CrossRefGoogle Scholar
5.Puignau, N., Sur la topologie de l'espace des application stables réeles vers l'espace projectif, Annales Inst. Fourier, à paraitre.Google Scholar
6.Steenrod, N. E., Homology with local coefficients, Annals Math. 44(2) (1943), 610–627.CrossRefGoogle Scholar
7.Welschinger, J.-Y., Invariants of real symplectic 4-manifolds and lower bounds in real enumerative geometry, Invent. Math. 162(1) (2005), 195–234.CrossRefGoogle Scholar
8.Welschinger, J.-Y., Enumerative invariants of strongly semipositive real symplectic sixmanifolds, prépublication de l'École Normale Supérieure de Lyon, version 2 (2007).Google Scholar