Article contents
THE p-COHOMOLOGY OF ALGEBRAIC VARIETIES AND SPECIAL VALUES OF ZETA FUNCTIONS
Published online by Cambridge University Press: 02 June 2014
Abstract
The 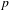 $p$-cohomology of an algebraic variety in characteristic
$p$-cohomology of an algebraic variety in characteristic 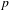 $p$ lies naturally in the category
$p$ lies naturally in the category 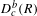 $D_{c}^{b}(R)$ of coherent complexes of graded modules over the Raynaud ring (Ekedahl, Illusie, Raynaud). We study homological algebra in this category. When the base field is finite, our results provide relations between the absolute cohomology groups of algebraic varieties, log varieties, algebraic stacks, etc., and the special values of their zeta functions. These results provide compelling evidence that
$D_{c}^{b}(R)$ of coherent complexes of graded modules over the Raynaud ring (Ekedahl, Illusie, Raynaud). We study homological algebra in this category. When the base field is finite, our results provide relations between the absolute cohomology groups of algebraic varieties, log varieties, algebraic stacks, etc., and the special values of their zeta functions. These results provide compelling evidence that 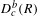 $D_{c}^{b}(R)$ is the correct target for
$D_{c}^{b}(R)$ is the correct target for 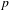 $p$-cohomology in characteristic
$p$-cohomology in characteristic 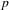 $p$.
$p$.
Keywords
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 4 , October 2015 , pp. 801 - 835
- Copyright
- © Cambridge University Press 2014
References
- 3
- Cited by


