Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
EISCHEN, ELLEN
HARRIS, MICHAEL
LI, JIANSHU
and
SKINNER, CHRISTOPHER
2020.
-ADIC -FUNCTIONS FOR UNITARY GROUPS.
Forum of Mathematics, Pi,
Vol. 8,
Issue. ,
Liu, Zheng
and
Rosso, Giovanni
2020.
Non-cuspidal Hida theory for Siegel modular forms and trivial zeros of p-adic L-functions.
Mathematische Annalen,
Vol. 378,
Issue. 1-2,
p.
153.
Loeffler, David
Pilloni, Vincent
Skinner, Christopher
and
Zerbes, Sarah Livia
2021.
Higher Hida theory and p-adic L-functions for GSp4.
Duke Mathematical Journal,
Vol. 170,
Issue. 18,
Liu, Zheng
2021.
Ordinary families of Klingen Eisenstein series on symplectic groups.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 5,
p.
3331.
Horinaga, Shuji
Pitale, Ameya
Saha, Abhishek
and
Schmidt, Ralf
2022.
The special values of the standard 𝐿-functions for 𝐺𝑆𝑝_{2𝑛}×𝐺𝐿₁.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 10,
p.
6947.
Eischen, Ellen
2022.
An introduction to Eisenstein measures.
Journal de Théorie des Nombres de Bordeaux,
Vol. 33,
Issue. 3.1,
p.
779.
Hsieh, Ming-Lun
and
Yamana, Shunsuke
2024.
Four-variable p-adic triple product L-functions and the trivial zero conjecture.
Mathematische Annalen,
Vol. 390,
Issue. 1,
p.
889.
Eischen, Ellen E.
and
Liu, Zheng
2024.
Archimedean zeta integrals for unitary groups.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Horinaga, Shuji
2024.
On the classification of $$({\mathfrak {g}},K)$$-modules generated by nearly holomorphic Hilbert–Siegel modular forms and projection operators.
Annales mathématiques du Québec,
Vol. 48,
Issue. 2,
p.
309.
Rodrigues Jacinto, Joaquín
and
Williams, Chris
2025.
An introduction to p-adic L-functions.
Essential Number Theory,
Vol. 4,
Issue. 1,
p.
101.
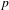 $p$-ADIC
$p$-ADIC  $L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
$L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS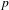 $p$-adic standard
$p$-adic standard  $L$-functions for ordinary families of Hecke eigensystems of the symplectic group
$L$-functions for ordinary families of Hecke eigensystems of the symplectic group 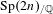 $\operatorname{Sp}(2n)_{/\mathbb{Q}}$ using the doubling method. We explain a clear and simple strategy of choosing the local sections for the Siegel Eisenstein series on the doubling group
$\operatorname{Sp}(2n)_{/\mathbb{Q}}$ using the doubling method. We explain a clear and simple strategy of choosing the local sections for the Siegel Eisenstein series on the doubling group 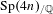 $\operatorname{Sp}(4n)_{/\mathbb{Q}}$, which guarantees the nonvanishing of local zeta integrals and allows us to
$\operatorname{Sp}(4n)_{/\mathbb{Q}}$, which guarantees the nonvanishing of local zeta integrals and allows us to 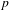 $p$-adically interpolate the restrictions of the Siegel Eisenstein series to
$p$-adically interpolate the restrictions of the Siegel Eisenstein series to 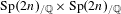 $\operatorname{Sp}(2n)_{/\mathbb{Q}}\times \operatorname{Sp}(2n)_{/\mathbb{Q}}$.
$\operatorname{Sp}(2n)_{/\mathbb{Q}}\times \operatorname{Sp}(2n)_{/\mathbb{Q}}$.