Article contents
ON TYPICALITY OF TRANSLATION FLOWS WHICH ARE DISJOINT WITH THEIR INVERSE
Published online by Cambridge University Press: 11 December 2018
Abstract
In this paper we prove that the set of translation structures for which the corresponding vertical translation flows are disjoint with its inverse contains a 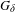 $G_{\unicode[STIX]{x1D6FF}}$-dense subset in every non-hyperelliptic connected component of the moduli space
$G_{\unicode[STIX]{x1D6FF}}$-dense subset in every non-hyperelliptic connected component of the moduli space 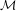 ${\mathcal{M}}$. This is in contrast to hyperelliptic case, where for every translation structure the associated vertical flow is reversible, i.e., it is isomorphic to its inverse by an involution. To prove the main result, we study limits of the off-diagonal 3-joinings of special representations of vertical translation flows. Moreover, we construct a locally defined continuous embedding of the moduli space into the space of measure-preserving flows to obtain the
${\mathcal{M}}$. This is in contrast to hyperelliptic case, where for every translation structure the associated vertical flow is reversible, i.e., it is isomorphic to its inverse by an involution. To prove the main result, we study limits of the off-diagonal 3-joinings of special representations of vertical translation flows. Moreover, we construct a locally defined continuous embedding of the moduli space into the space of measure-preserving flows to obtain the 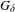 $G_{\unicode[STIX]{x1D6FF}}$-condition. Moreover, as a by-product we get that in every non-hyperelliptic connected component of the moduli space there is a dense subset of translation structures whose vertical flow is reversible.
$G_{\unicode[STIX]{x1D6FF}}$-condition. Moreover, as a by-product we get that in every non-hyperelliptic connected component of the moduli space there is a dense subset of translation structures whose vertical flow is reversible.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1677 - 1737
- Copyright
- © Cambridge University Press 2018
References
- 4
- Cited by



