Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-17T13:20:40.305Z Has data issue: false hasContentIssue false
  • English
  • Français

On the 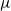$\mu $-invariant of the cyclotomic derivative of a Katz p-adic 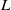$L$-function

Part of: Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  10 January 2014

Ashay A. Burungale
Ashay A. Burungale*
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095-1555, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

When the branch character has root number 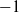$- 1$, the corresponding anticyclotomic Katz 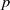$p$-adic 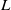$L$-function vanishes identically. For this case, we determine the 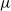$\mu $-invariant of the cyclotomic derivative of the Katz 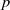$p$-adic 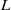$L$-function. The result proves, as an application, the non-vanishing of the anticyclotomic regulator of a self-dual CM modular form with root number 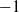$- 1$. The result also plays a crucial role in the recent work of Hsieh on the Eisenstein ideal approach to a one-sided divisibility of the CM main conjecture.

Keywords

Iwasawa invariant; Katz p-adic L-function; Hilbert modular Shimura variety; toric modular forms; anticyclotomic regulator

MSC classification

Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11R23: Iwasawa theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 1 , January 2015 , pp. 131 - 148
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agboola, A. and Howard, B., Anticyclotomic Iwasawa Theory of CM elliptic curves (with an appendix by K. Rubin) Ann. Inst. Fourier (Grenoble) 4 (6) (2006), 1374–1398.Google Scholar
Arnold, T., Anticyclotomic main conjectures for CM modular forms, J. Reine Angew. Math. 606 (2007), 41–78.Google Scholar
Hida, H. and Tilouine, J., Anticyclotomic Katz $p$ -adic $L$ -functions and congruence modules, Ann. Sci. Éc. Norm. Supér. (4) 26 (2) (1993), 189–259.Google Scholar
Hida, H., The Iwasawa $\mu $ -invariant of $p$ -adic Hecke $L$ -functions, Ann. of Math. 172 (1) (2010), 41–137.CrossRefGoogle Scholar
Hida, H., Vanishing of the $\mu $ -invariant of $p$ -adic Hecke $L$ -functions, Compos. Math. 147 (2011), 1151–1178.Google Scholar
Hsieh, M.-L., On the $\mu $ -invariant of anticyclotomic $p$ -adic $L$ -functions for CM fields, J. Reine Angew. Math., in press (available at http://www.math.ntu.edu.tw/~mlhsieh/research.htm) (2012), doi: 10.1515/crelle-2012-0056.Google Scholar
Hsieh, M.-L., On the non-vanishing of Hecke $L$ -values modulo $p$ , Amer. J. Math. 134 (6) (2012), 1503–1539.CrossRefGoogle Scholar
Hsieh, M.-L., Eisenstein congruence on unitary groups and Iwasawa main conjecture for CM fields, J. Amer. Math. Soc., in press (available at “ http://www.math.ntu.edu.tw/~mlhsieh/research.htm”) (2013).Google Scholar
Katz, N. M., $p$ -adic $L$ -functions for CM fields, Invent. Math. 49 (3) (1978), 199–297.Google Scholar
Murase, A. and Sugano, T., Local theory of primitive theta functions, Compos. Math. 123 (3) (2000), 273–302.Google Scholar
Rubin, K., The ‘main conjectures’ of Iwasawa theory for imaginary quadratic fields, Invent. Math. 103 (1) (1991), 25–68.Google Scholar
Tate, J., Number theoretic background, in Automorphic Forms, Representations and L-functions, Proceedings of Symposia in Pure Mathematics XXXIII, Part 2, pp. 3–26 (American Mathematical Society, Providence, RI, 1979).CrossRefGoogle Scholar