Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T07:16:44.846Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE GROWTH OF TORSION IN THE COHOMOLOGY OF ARITHMETIC GROUPS

Part of: Computational number theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  21 March 2018

A. Ash ,
P. E. Gunnells ,
M. McConnell  and
D. Yasaki
A. Ash
Affiliation:
Boston College, Chestnut Hill, MA 02467, USA ([email protected])
P. E. Gunnells
Affiliation:
Department of Mathematics and Statistics, University of Massachusetts, Amherst, MA 01003-9305, USA ([email protected])
M. McConnell
Affiliation:
Princeton University, Princeton, NJ 08540, USA ([email protected])
D. Yasaki
Affiliation:
Department of Mathematics and Statistics, University of North Carolina at Greensboro, Greensboro, NC 27412, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 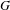$G$ be a semisimple Lie group with associated symmetric space 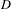$D$, and let 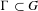$\unicode[STIX]{x1D6E4}\subset G$ be a cocompact arithmetic group. Let 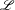$\mathscr{L}$ be a lattice inside a $\mathbb{Z}\unicode[STIX]{x1D6E4}$-module arising from a rational finite-dimensional complex representation of 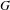$G$. Bergeron and Venkatesh recently gave a precise conjecture about the growth of the order of the torsion subgroup 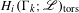$H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}$ as 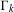$\unicode[STIX]{x1D6E4}_{k}$ ranges over a tower of congruence subgroups of 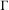$\unicode[STIX]{x1D6E4}$. In particular, they conjectured that the ratio 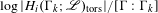$\log |H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}|/[\unicode[STIX]{x1D6E4}:\unicode[STIX]{x1D6E4}_{k}]$ should tend to a nonzero limit if and only if 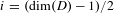$i=(\dim (D)-1)/2$ and 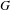$G$ is a group of deficiency $1$. Furthermore, they gave a precise expression for the limit. In this paper, we investigate computationally the cohomology of several (non-cocompact) arithmetic groups, including 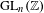$\operatorname{GL}_{n}(\mathbb{Z})$ for 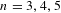$n=3,4,5$ and 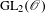$\operatorname{GL}_{2}(\mathscr{O})$ for various rings of integers, and observe its growth as a function of level. In all cases where our dataset is sufficiently large, we observe excellent agreement with the same limit as in the predictions of Bergeron–Venkatesh. Our data also prompts us to make two new conjectures on the growth of torsion not covered by the Bergeron–Venkatesh conjecture.

Keywords

cohomology of arithmetic groupsGalois representationstorsion in cohomology

MSC classification

Primary: 11F75: Cohomology of arithmetic groups
Secondary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols 11F80: Galois representations 11Y99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 537 - 569
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors thank the Banff International Research Station and Wesleyan University, where some work was carried out on this paper. A. A. was partially supported by NSA grant H98230-09-1-0050. P. G. was partially supported by NSF grants DMS 1101640 and 1501832. D. Y. was partially supported by NSA grant H98230-15-1-0228. This manuscript is submitted for publication with the understanding that the United States government is authorized to produce and distribute reprints.

References

Ash, A., Galois representations attached to mod p cohomology of GL(n, Z), Duke Math. J. 65(2) (1992), 235–255.Google Scholar
Ash, A., Parity of mod p Betti numbers, Bol. Soc. Mat. Mexicana (3) 5(1) (1999), 79–85.Google Scholar
Ash, A., Gunnells, P. E. and McConnell, M., Cohomology of congruence subgroups of SL4(ℤ), J. Number Theory 94(1) (2002), 181–212.Google Scholar
Ash, A., Gunnells, P. E. and McConnell, M., Torsion in the cohomology of congruence subgroups of SL(4, ℤ) and Galois representations, J. Algebra 325 (2011), 404–415.Google Scholar
Ash, A., Gunnells, P. E. and McConnell, M., Resolutions of the Steinberg module for GL (n), J. Algebra 349 (2012), 380–390.Google Scholar
Ash, A., Gunnells, P. E. and McConnell, M., Mod 2 homology for GL(4) and Galois representations, J. Number Theory 146 (2015), 4–22.Google Scholar
Ash, A. and McConnell, M., Experimental indications of three-dimensional Galois representations from the cohomology of SL(3, Z), Exp. Math. 1(3) (1992), 209–223.Google Scholar
Bergeron, N. and Venkatesh, A., The asymptotic growth of torsion homology for arithmetic groups, J. Inst. Math. Jussieu 12(2) (2013), 391–447.Google Scholar
Bhargava, M., Mass formulae for extensions of local fields, and conjectures on the density of number field discriminants, Int. Math. Res. Not. IMRN (17) (2007), Art. ID rnm 052, 20.Google Scholar
Borel, A., Commensurability classes and volumes of hyperbolic 3-manifolds, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 8(1) (1981), 1–33.Google Scholar
Borel, A. and Serre, J.-P., Corners and arithmetic groups, Comment. Math. Helv. 48 (1973), 436–491. Avec un appendice: Arrondissement des variétés à coins, par A. Douady et L. Hérault.Google Scholar
Calegari, F. and Venkatesh, A., A torsion Jacquet–Langlands correspondence, (2012), submitted.Google Scholar
Cremona, J. E., Hyperbolic tessellations, modular symbols, and elliptic curves over complex quadratic fields, Compos. Math. 51(3) (1984), 275–324.Google Scholar
Dutour Sikirić, M., Gangl, H., Gunnells, P. E., Hanke, J., Schürmann, A. and Yasaki, D., On the cohomology of linear groups over imaginary quadratic fields, J. Pure Appl. Algebra 220(7) (2016), 2564–2589.Google Scholar
Elbaz-Vincent, P., Gangl, H. and Soulé, C., Quelques calculs de la cohomologie de GLN(ℤ) et de la K-théorie de ℤ, C. R. Math. Acad. Sci. Paris 335(4) (2002), 321–324.Google Scholar
Elbaz-Vincent, P., Gangl, H. and Soulé, C., Perfect forms, K-theory and the cohomology of modular groups, Adv. Math. 245 (2013), 587–624.Google Scholar
Elstrodt, J., Grunewald, F. and Mennicke, J., On the group PSL2(Z[i]), in Number Theory Days, 1980 (Exeter, 1980), London Mathematical Society Lecture Note Series, Volume 56, pp. 255–283 (Cambridge University Press, Cambridge, 1982).Google Scholar
Elstrodt, J., Grunewald, F. and Mennicke, J., Groups acting on hyperbolic space, in Springer Monographs in Mathematics, Harmonic Analysis and Number Theory, (Springer, Berlin, 1998).Google Scholar
Franke, J., Harmonic analysis in weighted L 2 -spaces, Ann. Sci. Éc. Norm. Supér. (4) 31(2) (1998), 181–279.Google Scholar
Gunnells, P. E., Hajir, F. and Yasaki, D., Modular forms and elliptic curves over the field of fifth roots of unity, Exp. Math. 22(2) (2013), 203–216.Google Scholar
Gunnells, P. E. and Yasaki, D., Modular forms and elliptic curves over the cubic field of discriminant - 23, Int. J. Number Theory 9(1) (2013), 53–76.Google Scholar
Harder, G., Eisenstein cohomology of arithmetic groups and its applications to number theory, in Proceedings of the International Congress of Mathematicians, Volumes I, II (Kyoto, 1990), pp. 779–790 (Math. Soc. Japan, Tokyo, 1991).Google Scholar
Hurwitz, A., Ueber die Reduction der binären quadratischen Formen, Math. Ann. 45(1) (1894), 85–117.Google Scholar
Koecher, M., Beiträge zu einer Reduktionstheorie in Positivitätsbereichen. I, Math. Ann. 141 (1960), 384–432.Google Scholar
Li, J.-S. and Schwermer, J., Automorphic representations and cohomology of arithmetic groups, in Challenges for the 21st Century (Singapore, 2000), pp. 102–137 (World Sci. Publ., River Edge, NJ, 2001).Google Scholar
Pfaff, J., Exponential growth of homological torsion for towers of congruence subgroups of Bianchi groups, Ann. Global Anal. Geom. 45(4) (2014), 267–285.Google Scholar
Priplata, C., Cohomology and homology of $PSL_{2}$ over imaginary quadratic integers with general coefficients $M_{n,m}(O_{K})$ and Hecke eigenvalues, Ph.D. thesis, Heinrich Heine Universität, Düsseldorf, 2000.Google Scholar
Scholze, P., On torsion in the cohomology of locally symmetric varieties, Ann. of Math. (2) 182(3) (2015), 945–1066.Google Scholar
Şengün, M. H., On the integral cohomology of Bianchi groups, Exp. Math. 20(4) (2011), 487–505.Google Scholar
Voronoǐ, G., Sur quelques propriétés des formes quadratiques positives parfaites, J. Reine Angew. Math. 133 (1908), 97–178.Google Scholar