Article contents
ON THE GEOMETRY OF THE PAPPAS–RAPOPORT MODELS FOR PEL SHIMURA VARIETIES
Published online by Cambridge University Press: 18 February 2022
Abstract
In this article we study integral models of Shimura varieties, called Pappas–Rapoport splitting model, for ramified P.E.L. Shimira data. We study the special fiber and some stratification of these models, in particular we show that these are smooth and the Rapoport locus and the 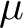 $\mu $-ordinary locus are dense, under some condition on the ramification.
$\mu $-ordinary locus are dense, under some condition on the ramification.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 5 , September 2023 , pp. 2403 - 2445
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 2
- Cited by



