Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-20T18:36:44.398Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DISTRIBUTION OF THE MAXIMUM OF CUBIC EXPONENTIAL SUMS

Part of: Finite fields and commutative rings (number-theoretic aspects) Exponential sums and character sums Limit theorems (Co)homology theory

Published online by Cambridge University Press:  27 September 2018

Youness Lamzouri
Youness Lamzouri*
Affiliation:
Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, ON M3J1P3, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate the distribution of the maximum of partial sums of certain cubic exponential sums, commonly known as ‘Birch sums’. Our main theorem gives upper and lower bounds (of nearly the same order of magnitude) for the distribution of large values of this maximum, that hold in a wide uniform range. This improves a recent result of Kowalski and Sawin. The proofs use a blend of probabilistic methods, harmonic analysis techniques, and deep tools from algebraic geometry. The results can also be generalized to other types of 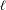$\ell$-adic trace functions. In particular, the lower bound of our result also holds for partial sums of Kloosterman sums. As an application, we show that there exist 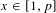$x\in [1,p]$ and 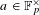$a\in \mathbb{F}_{p}^{\times }$ such that 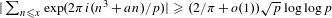$|\sum _{n\leqslant x}\exp (2\unicode[STIX]{x1D70B}i(n^{3}+an)/p)|\geqslant (2/\unicode[STIX]{x1D70B}+o(1))\sqrt{p}\log \log p$. The uniformity of our results suggests that this bound is optimal, up to the value of the constant.

Keywords

Birch sumsExponential sumsSato–Tate distributionl-adic trace functionsRiemann hypothesis over finite fields

MSC classification

Primary: 11L03: Trigonometric and exponential sums, general 11T23: Exponential sums
Secondary: 14F20: Étale and other Grothendieck topologies and (co)homologies 60F10: Large deviations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 4 , July 2020 , pp. 1259 - 1286
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is partially supported by a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada.

References

Birch, B. J., How the number of points of an elliptic curve over a fixed prime field varies, J. Lond. Math. Soc. (2) 43 (1968), 57–60.Google Scholar
Bonolis, D., Applications of the Riemann hypothesis over finite fields in analytic number theory, Ph.D. Thesis, ETH Zurich.Google Scholar
Bober, J. W., Goldmakher, L., Granville, A. and Koukoulopoulos, D., The frequency and the structure of large character sums, J. Eur. Math. Soc. 58, arXiv:1410.8189, to appear.Google Scholar
Fouvry, E., Kowalski, E. and Michel, P., Algebraic trace functions over the primes, Duke Math. J. 163(9) (2014), 1683–1736.Google Scholar
Fouvry, E., Kowalski, E. and Michel, P., Trace functions over finite fields and their applications, in Colloquium De Giorgi 2013 and 2014, Colloquia, Volume 5, pp. 7–35 (Ed. Norm., Pisa, 2014).Google Scholar
Fouvry, E., Kowalski, E. and Michel, P., A study in sums of products, Philos. Trans. R. Soc. A 373(2040) (2015), 20140309.Google Scholar
Fouvry, E., Kowalski, E., Michel, P., Raju, C. S., Rivat, J. and Soundararajan, K., On short sums of trace functions, Ann. Inst. Fourier (Grenoble) 67(1) (2017), 423–449.Google Scholar
Granville, A. and Soundararajan, K., Extreme values of 𝜁(1 + it), in The Riemann Zeta Function and Related Themes: Papers in Honor of Professor K. Ramachandra, Ramanujan Mathematical Society Lecture Notes Series, Volume 2, pp. 65–80 (Ramanujan Mathematical Society, India, 2006).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, Volume 53, p. xii+615 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Katz, N. M., On the monodromy attached to certain families of exponential sums, Duke Math. J. 54 (1987), 41–56.Google Scholar
Kowalski, E. and Sawin, W., Kloosterman paths and the shape of exponential sums, Compos. Math. 152(7) (2016), 1489–1516.Google Scholar
Kowalski, E. and Sawin, W., On the support of the Kloosterman paths, Preprint, arXiv:1709.05192, 26 pages.Google Scholar
Livné, R., The average distribution of cubic exponential sums, J. Reine Angew. Math. 375–376 (1987), 362–379.Google Scholar
Liu, J., Royer, E. and Wu, J., On a conjecture of Montgomery–Vaughan on extreme values of automorphic L-functions at 1, in Anatomy of Integers, CRM Proceedings Lecture Notes, Volume 46, pp. 217–245 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Montgomery, H. L. and Vaughan, R. C., Exponential sums with multiplicative coefficients, Invent. Math. 43(1) (1977), 69–82.Google Scholar
Perret-Gentil, C., Gaussian distribution of short sums of trace functions over finite fields, Math. Proc. Cambridge Philos. Soc. 163(3) (2017), 385–422.Google Scholar
Perret-Gentil, C., Distribution questions for trace functions with values in cyclotomic integers and their reductions, Trans. Amer. Math. Soc. 48, arXiv:1610.05087, to appear.Google Scholar