Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T18:59:01.711Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE COHOMOLOGY OF SOME SIMPLE SHIMURA VARIETIES WITH BAD REDUCTION

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  06 December 2016

Xu Shen Open the ORCID record for Xu Shen [Opens in a new window]
Xu Shen*
Affiliation:
Fakultät für Mathematik, Universität Regensburg, Universitaetsstr. 31, 93040 Regensburg, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the Galois representations inside the 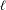$\ell$-adic cohomology of some quaternionic and related unitary Shimura varieties at ramified places. The main results generalize the previous works of Reimann and Kottwitz in this setting to arbitrary levels at 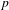$p$, and confirm the expected description of the cohomology due to Langlands and Kottwitz.

Keywords

Shimura varietiesquaternion algebrascohomology

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties
Secondary: 14G35: Modular and Shimura varieties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 1 , January 2019 , pp. 1 - 24
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Current address: Morningside Center of Mathematics, No. 55, Zhongguancun East Road, Beijing 100190, China. E-mail: [email protected]

References

Arthur, J. and Clozel, L., Simple Algebras, Base Change, and the Advanced Theory of the Trace Formula, Annals of Mathematics Studies, 120 (Princeton University Press, Princeton, NJ, 1989).Google Scholar
Aubert, A.-M., Baum, P., Plymen, R. and Solleveld, M., The local Langlands correspondence for inner forms of $\text{SL}_{n}$ , Res. Math. Sci. (to appear) arXiv:1305.2638.Google Scholar
Boutot, J.-F. and Zink, T., The $p$ -adic uniformization of Shimura curves, Preprint 95-107, Universität Bielefeld (1995), available at https://www.math.uni-bielefeld.de/∼zink/p-adicuni.ps.Google Scholar
Deligne, P., Kazhdan, D. and Vign’eras, M.-F., Représentations des algèbres centrales simples p-adiques, in Représentations des groupes réductifs sur un corps local, pp. 33–117 (Hermann, Paris, 1984).Google Scholar
Görtz, U., On the flatness of models of certain Shimura varieties of PEL-type, Math. Ann. 321 (2001), 689–727.Google Scholar
Haines, T. J., The stable Bernstein center and test functions for Shimura varieties, in Automorphic Forms and Galois Representations, London Mathematical Society Lecture Note Series, 415, Volume 2, pp. 118–186 (Cambridge University Press, 2014).Google Scholar
Harris, M. and Taylor, R., The Geometry and Cohomology of some Simple Shimura Varieties, Annals of Mathematics Studies, 151 (Princeton University Press, Princeton, NJ, 2001).Google Scholar
Kottwitz, R. E., Shimura varieties and twisted orbital integrals, Math. Ann. 269 (1984), 287–300.Google Scholar
Kottwitz, R. E., Shimura varieties and 𝜆-adic representations, in Perspect. Math. 10, Volume 1, pp. 161–209 (Academic Press, 1990).Google Scholar
Kottwitz, R. E., Points on some Shimura varieties over finite fields, J. Amer. Math. Soc. 5 (1992), 373–444.Google Scholar
Kottwitz, R. E., Isocrystals with additional structure II, Compositio. Math. 109(3) (1997), 255–339.Google Scholar
Kottwitz, R. E., On the 𝜆-adic representations associated to some simple Shimura varieties, Invent. Math. 108(3) (1992), 653–665.Google Scholar
Langlands, R. P., On the zeta function of some simple Shimura varieties, Canad. J. Math. 31 (1979), 1121–1216.Google Scholar
Milne, J. S., The points on a Shimura variety modulo a prime of good reduction, in The Zeta Functions of Picard Modular Surfaces, (ed. Langlands, R. P. and Ramakrishnan, D.), pp. 151–253 (CRM, 1992).Google Scholar
Rapoport, M., On the local zeta function of quaternionic Shimura varieties with bad reduction, Math. Ann. 279 (1988), 673–697.Google Scholar
Rapoport, M., On the bad reduction of Shimura varieties, in Automorphic Forms, Shimura varieties, and L-Functions, Perspect. Math., 11, Volume 2, pp. 77–160 (Academic Press, 1990).Google Scholar
Rapoport, M., A guide to reduction modulo p of Shimura varieties, Astérisique 298 (2005), 271–318.Google Scholar
Rapoport, M. and Zink, T., Period Spaces for p-divisible Groups, Annals of Mathematics Studies, 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
Reimann, H., The Semi-Simple Zeta Function of Quaternionic Shimura Varieties, Lecture Notes in Mathematics, 1657 (Springer, Berlin, 1997).Google Scholar
Reimann, H., On the zeta function of quaternionic Shimura varieties, Math. Ann. 317 (2000), 41–55.Google Scholar
Reimann, H., Reduction of quaternionic Shimura varieties at parahoric levels, Manuscripta Math. 107(3) (2002), 355–390.Google Scholar
Reimann, H., Cohomology of quaternionic Shimura varieties at parahoric levels, Manuscripta Math. 107(3) (2002), 391–407.Google Scholar
Rogawski, J., Representations of GL(n) and division algebras over a p-adic field, Duke Math. J. 50 (1983), 161–169.Google Scholar
Scholze, P., The Langlands–Kottwitz approach for some simple Shimura varieties, Invent. Math. 192(3) (2013), 627–661.Google Scholar
Scholze, P., The local Langlands correspondence for GL n over p-adic fields, Invent. Math. 192(3) (2013), 663–715.Google Scholar
Scholze, P., The Langlands–Kottwitz method and deformation spaces of p-divisible groups, J. Amer. Math. Soc. 26(1) (2013), 227–259.Google Scholar
Scholze, P. and Shin, S.-W., On the cohomology of compact unitary group Shimura varieties at ramified split places, J. Amer. Math. Soc. 26(1) (2013), 261–294.Google Scholar
Shen, X., On the $\ell$ -adic cohomology of some $p$ -adically uniformized Shimura varieties, J. Inst. Math. Jussieu (to appear) arXiv:1411.0244.Google Scholar
Tian, Y. and Xiao, L., On Goren-Oort stratification for quaternionic Shimura varieties, Compos. Math. (to appear) arXiv:1308.0790.Google Scholar
Varshavsky, Y., Lefschetz–Verdier trace formula and a generalization of a theorem of Fujiwara, Geom. Funct. Anal. 17(1) (2007), 271–319.Google Scholar