Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-21T10:25:33.390Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SOME CONSEQUENCES OF A THEOREM OF J. LUDWIG

Part of: Algebraic number theory: local and $p$-adic fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  27 September 2021

Vytautas Paškūnas Open the ORCID record for Vytautas Paškūnas [Opens in a new window]
Vytautas Paškūnas*
Affiliation:
Universität Duisburg-Essen, Fakultät für Mathematik, 45117Essen, Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove some qualitative results about the p-adic Jacquet–Langlands correspondence defined by Scholze, in the 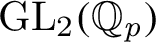$\operatorname {\mathrm {GL}}_2(\mathbb{Q}_p )$ residually reducible case, using a vanishing theorem proved by Judith Ludwig. In particular, we show that in the cases under consideration, the global p-adic Jacquet–Langlands correspondence can also deal with automorphic forms with principal series representations at p in a nontrivial way, unlike its classical counterpart.

Keywords

p-adic Jacquet–Langlands correspondencep-adic automorphic forms

MSC classification

Primary: 11S37: Langlands-Weil conjectures, nonabelian class field theory
Secondary: 11F85: $p$-adic theory, local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 1067 - 1106
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Allen, P. and Calegari, F., Finiteness of unramified deformation rings, Algebra Number Theory 8(9) (2014), 2263–2272.CrossRefGoogle Scholar
Ardakov, K. and Brown, K. A., Ring-theoretic properties of Iwasawa algebras: A survey, Doc. Math. extra vol. (2006), 7–33.Google Scholar
Demazure, M. and Grothendieck, A. (Eds.), Schémas en groupes (SGA 3). Tome I. Propriétés générales des schémas en groupes. (French) [Group schemes (SGA 3), Vol. I. General properties of group schemes] Séminaire de Géométrie Algébrique du Bois Marie 1962–64. [Algebraic Geometry Seminar of Bois Marie 1962–64] (Berlin, Heidelberg, Springer-Verlag, 1970, French edition). Revised and annotated by P. Gille and P. Polo, Documents Mathématiques (Paris) [Mathematical Documents (Paris)], 7 (Paris, Société Mathématique de France, 2011), xxviii+610 pp. ISBN: 978-2-85629-323-2.Google Scholar
Barthel, L. and Livné, R., Irreducible modular representations of $\mathrm{GL}_2$ of a local field, Duke Math. J. 75(2) (1994), 261–292.CrossRefGoogle Scholar
Berger, L. and Breuil, C., Sur quelques représentations potentiellement cristallines de $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ , Astérisque 330 (2010), 155–211.Google Scholar
Breuil, C., Sur quelques représentations modulaires et $p$ -adiques de $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ : I, Compos. Math. 138 (2003), 165–188.CrossRefGoogle Scholar
Breuil, C., Sur quelques représentations modulaires et $p$ -adiques de $\mathrm{GL}_2\left({\mathbb{Q}}p\right)$ : II, J. Inst. Math. Jussieu 2 (2003), 1–36.CrossRefGoogle Scholar
Breuil, C. and Emerton, M., Représentations $p$ -adiques ordinaires de $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ et compatibilité local-global, Astérisque 331 (2010), 255–315.Google Scholar
Breuil, C. and Mézard, A., Multiplicités modulaires et représentations de $\mathrm{GL}_2\left(\mathbb{Z}{p}\right)$ et de $\mathrm{Gal}(\overline{\mathbb{Q}}p/\mathbb{Q}{p})$ en $l=p$ , Duke Math. J. 115 (2002), 205–310.CrossRefGoogle Scholar
Brumer, A., Pseudocompact algebras, profinite groups and class formations, J. Algebra 4 (1966), 442–470.CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the $p$ -adic Langlands program for $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ , Compos. Math. 154(3) (2018), 503–548.CrossRefGoogle Scholar
Chojecki, P. and Knight, E., $p$ -adic Jacquet-Langlands correspondence and patching, Preprint, 2017, https://arxiv.org/abs/1709.10306.Google Scholar
Colmez, P., Représentations de $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ et $\left(\varphi, \varGamma \right)$ -modules, Astérisque 330 (2010), 281–509.Google Scholar
Colmez, P., Représentations triangulines de dimension $2$ , Astérisque 319 (2008), 213–258.Google Scholar
Colmez, P., Dospinescu, G. and Paškūnas, V., The $p$ -adic local Langlands correspondence for $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ , Camb. J. Math. 2(1) (2014), 1–47.CrossRefGoogle Scholar
Deligne, P. and Serre, J.-P., Formes modulaires de poids $1$ , Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 507–530.CrossRefGoogle Scholar
Artin, M., Grothendieck, A. and Verdier, J. L., Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos. (French) Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4). Lecture Notes in Mathematics, Vol. 269 (Berlin-New York, Springer-Verlag, 1972), xix+525 pp.CrossRefGoogle Scholar
Emerton, M., Local-global compatibility in the $p$ -adic Langlands programme for $\mathrm{GL}_2/\mathbb{Q}$ , Preprint, 2011, http://www.math.uchicago.edu/~emerton/pdffiles/lg.pdf.Google Scholar
Emerton, M., On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms, Invent. Math. 164(1) (2006), 1–84.CrossRefGoogle Scholar
Emerton, M., Ordinary parts of admissible representations of $p$ -adic reductive groups I. Definition and first properties, Astérisque 331 (2010), 335–381.Google Scholar
Emerton, M. and Paškūnas, V., On the density of supercuspidal points of fixed regular weight in local deformation rings and global Hecke algebras, J. Éc. polytech. Math. 7 (2020), 337–371.CrossRefGoogle Scholar
Gee, T. and Geraghty, D., The Breuil-Mézard conjecture for quaternion algebras, Ann. Inst. Fourier (Grenoble) 65(4) (2015), 1557–1575.CrossRefGoogle Scholar
Gee, T. and Newton, J., Patching and the completed homology of locally symmetric spaces, J. Inst. Math. Jussieu, (2019) https://arxiv.org/abs/1609.06965.Google Scholar
Henniart, G., Sur l’unicité des types pour $\mathrm{GL}_2$ , appendix to [9].Google Scholar
Howe, S., Overconvergent modular forms and the $p$ -adic Jacquet-Langlands correspondence (PhD thesis), 2017, https://knowledge.uchicago.edu/record/787.Google Scholar
Hu, Y., Multiplicities of cohomological automorphic forms on $\mathrm{GL}_2$ and mod $p$ representations of $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ , J. Eur. Math. Soc., (2020), https://arxiv.org/abs/1801.10074.Google Scholar
Kisin, M., Deformations of ${G}_{\mathbb{Q}{p}}$ and $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ representations, Astérisque 330 (2010), 511–528.Google Scholar
Kisin, M., Moduli of finite flat group schemes and modularity, Ann. of Math. (2), 170 (2009), 1085–1180.CrossRefGoogle Scholar
Kohlhaase, J., Smooth duality in natural characteristic, Adv. Math. 317 (2017), 1–49.CrossRefGoogle Scholar
Levasseur, T., Some properties of non-commutative regular graded rings, Glasg. Math. J. 34(3) (1992), 277–300.CrossRefGoogle Scholar
Ludwig, J., A quotient of the Lubin-Tate tower, Forum Math. Sigma 5 (2017), e17.CrossRefGoogle Scholar
Matsumura, H., Commutative Ring Theory , Second Edition, Cambridge Stud. Adv. Math. 8 (Cambridge, Cambridge University Press, 1989).Google Scholar
Morra, S., Invariant elements for $p$ -modular representations of $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ , Trans. Amer. Math. Soc. 365 (2013), 6625–6667.CrossRefGoogle Scholar
Newton, J., Completed cohomology of Shimura curves and a $p$ -adic Jacquet-Langlands correspondence, Math. Ann. 355(2) (2013), 729–763.CrossRefGoogle Scholar
Paškūnas, V., Admissible unitary completions of locally $\mathbb{Q}{p}$ -rational representations of $\mathrm{GL}_2(F)$ , Represent. Theory 14 (2010), 324–354.CrossRefGoogle Scholar
Paškūnas, V., Extensions for supersingular representations of $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ , Astérisque 331 (2010), 317–353.Google Scholar
Paškūnas, V., The image of Colmez’s Montreal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191.CrossRefGoogle Scholar
Paškūnas, V., Blocks for mod $p$ representations of $\mathrm{GL}_2\left(\mathbb{Q}{p}\right)$ , in Automorphic Forms and Galois Representations, Vol. 2, London Math. Soc. Lecture Note Ser. 415 (Cambridge, Cambridge University Press, 2014), 231–247.Google Scholar
Paškūnas, V., On the Breuil–Mézard Conjecture, Duke Math. J. 164(2) (2015), 297–359.CrossRefGoogle Scholar
Paškūnas, V., On $2$ -dimensional $2$ -adic Galois representations of local and global fields, Algebra Number Theory 10(6) (2016), 1301–1358.CrossRefGoogle Scholar
Paškūnas, V., On $2$ -adic deformations, Math. Z. 286(3-4) (2017), 801–819.CrossRefGoogle Scholar
Persiflage, Finiteness of the global deformation ring over local deformation rings, 2013, https://galoisrepresentations.wordpress.com/2013/05/18/finiteness-of-the-global-deformation-ring-over-local-deformation-rings/ Google Scholar
Schmidt, T. and Strauch, M., Dimensions of some locally analytic representations, Represent. Theory 20 (2016), pp. 14–38.CrossRefGoogle Scholar
Schneider, P., Nonarchimedean Functional Analysis (Berlin, Springer, 2001).Google Scholar
Schneider, P. and Teitelbaum, J., $U(\mathfrak{g})$ -finite locally analytic representations, Represent. Theory 5 (2001), 111–128.CrossRefGoogle Scholar
Schneider, P. and Teitelbaum, J., Banach space representations and Iwasawa theory, Israel J. Math. 127 (2002), 359–380.CrossRefGoogle Scholar
Scholze, P., On the $p$ -adic cohomology of the Lubin-Tate tower, Ann. Sci. Éc. Norm. Supér. (4) 51(4) (2018), 811–863.CrossRefGoogle Scholar
Taylor, R., On the meromorphic continuation of degree two $L$ -functions, Doc. Math. extra vol., ‘John Coates’ Sixtieth Birthday’ (2006), 729–779.Google Scholar
Venjakob, O., On the structure theory of the Iwasawa algebra of a $p$ -adic Lie group, J. Eur. Math. Soc. JEMS 4(3) (2002), 271–311.CrossRefGoogle Scholar
Wilson, J. S., Profinite Groups , London Mathematical Society Monographs New Series 19 (New York, Oxford University Press, 1998) Google Scholar