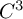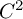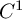Several dynamical properties of maps or flows strongly depend on the behavior at fixed points or singularities of vector fields, respectively. Normal forms then become a crucial tool for their study. There is a huge literature in this regard for complex analytic maps. In particular, a complete classification in the one-dimensional (1-D) case follows from the work of Écalle [Reference Écalle6], Martinet and Ramis [Reference Martinet and Ramis12] and Voronin [Reference Voronin22]. The real 1-D case was treated by Takens [Reference Takens21] in the
![]() $C^{\infty }$
setting and later studied by Yoccoz [Reference Yoccoz23] in finite regularity. It follows from their works that, for a nonflat germ of diffeomorphism, the associated vector field, that is, the unique
$C^{\infty }$
setting and later studied by Yoccoz [Reference Yoccoz23] in finite regularity. It follows from their works that, for a nonflat germ of diffeomorphism, the associated vector field, that is, the unique
![]() $C^1$
vector field whose time-1 map yields the germ, first constructed by Szekeres [Reference Szekeres20], has the expected regularity (
$C^1$
vector field whose time-1 map yields the germ, first constructed by Szekeres [Reference Szekeres20], has the expected regularity (
![]() $C^{\infty }$
in case of a germ of smooth maps,
$C^{\infty }$
in case of a germ of smooth maps,
![]() $C^{k-1}$
for a germ of
$C^{k-1}$
for a germ of
![]() $C^k$
diffeomorphisms). This certainly has direct consequences for the conjugacy classes of the corresponding germs of diffeomorphisms, yet these are explicit only in [Reference Takens21], with no mention in [Reference Yoccoz23]. This work arose from the necessity of clarifying this issue. More interestingly, some of our results go beyond a direct translation of those of Takens and Yoccoz and reveal several unexpected rigidity phenomena for low-regular conjugacies.
$C^k$
diffeomorphisms). This certainly has direct consequences for the conjugacy classes of the corresponding germs of diffeomorphisms, yet these are explicit only in [Reference Takens21], with no mention in [Reference Yoccoz23]. This work arose from the necessity of clarifying this issue. More interestingly, some of our results go beyond a direct translation of those of Takens and Yoccoz and reveal several unexpected rigidity phenomena for low-regular conjugacies.
Most of this work will deal with germs of diffeomorphisms of the real line fixing the origin. To simplify, we will restrict the discussion to orientation-preserving (germs of) maps; extending the results/examples to the orientation-reversing case is straightforward. Moreover, we will slightly modify the notion of germ by considering only right neighborhoods of the origin. In other words, a germ in this setting will be an equivalence class of diffeomorphisms of intervals of the form
![]() $[0,\eta )$
, with
$[0,\eta )$
, with
![]() $\eta> 0$
, where two maps are equivalent if they coincide on some interval
$\eta> 0$
, where two maps are equivalent if they coincide on some interval
![]() $[0,\eta ')$
, with
$[0,\eta ')$
, with
![]() $\eta '> 0$
. Definitively, this definition is more adapted to the 1-D context; moreover, one can easily retrieve analogous results for the original notion starting from those in this setting.
$\eta '> 0$
. Definitively, this definition is more adapted to the 1-D context; moreover, one can easily retrieve analogous results for the original notion starting from those in this setting.
In the framework above, an obvious conjugacy invariant is the value of the derivative at the fixed point. In the hyperbolic case, this value is a complete invariant of
![]() $C^{1+\tau }$
conjugacy. (The
$C^{1+\tau }$
conjugacy. (The
![]() $C^1$
case is different and rather special; see [Reference Eynard-Bontemps and Navas8].) For nonflat parabolic germs, the first invariant is the order of contact to the identity at the origin. Although the sign of the corresponding coefficient in the Taylor series expansion is invariant under conjugacy by germs of orientation-preserving maps, its value is not, as it can be easily modified by conjugacies by homotheties. However, there is a number that yields another obstruction to conjugacy: the residue
$C^1$
case is different and rather special; see [Reference Eynard-Bontemps and Navas8].) For nonflat parabolic germs, the first invariant is the order of contact to the identity at the origin. Although the sign of the corresponding coefficient in the Taylor series expansion is invariant under conjugacy by germs of orientation-preserving maps, its value is not, as it can be easily modified by conjugacies by homotheties. However, there is a number that yields another obstruction to conjugacy: the residue
![]() $\mathrm {Res}$
. Together with its companion, the iterative residue
$\mathrm {Res}$
. Together with its companion, the iterative residue
![]() $\mathrm {Resit}$
, this is a very well-known object in the complex setting and extends to nonflat germs of regular-enough (for instance, real-analytic) diffeomorphisms as follows: Start with a parabolic germ of the form
$\mathrm {Resit}$
, this is a very well-known object in the complex setting and extends to nonflat germs of regular-enough (for instance, real-analytic) diffeomorphisms as follows: Start with a parabolic germ of the form
Such a germ will be said to be exactly
![]() $\ell $
-tangent to the identity. Moreover, f will be said to be (topologically) expanding (resp. contracting) if the value of the coefficient
$\ell $
-tangent to the identity. Moreover, f will be said to be (topologically) expanding (resp. contracting) if the value of the coefficient
![]() $a_{\ell +1}$
above is positive (resp. negative). This is equivalent to that
$a_{\ell +1}$
above is positive (resp. negative). This is equivalent to that
![]() $f(x)> x$
(resp.
$f(x)> x$
(resp.
![]() $f(x) < x$
) for all small-enough
$f(x) < x$
) for all small-enough
![]() $x> 0$
. A very well-known lemma claims that f is conjugate by a germ of diffeomorphism to a germ of the (reduced) form
$x> 0$
. A very well-known lemma claims that f is conjugate by a germ of diffeomorphism to a germ of the (reduced) form
where the sign above is
![]() $+$
(resp.
$+$
(resp.
![]() $-$
) in the expanding (resp. contracting) case. Moreover, the value of
$-$
) in the expanding (resp. contracting) case. Moreover, the value of
![]() $\mu $
is uniquely determined. One then defines
$\mu $
is uniquely determined. One then defines
By definition, these expressions are invariant under conjugacy.
In §1, we put this construction in a more algebraic perspective. In particular, we consider formal germs of diffeomorphisms at the origin (or changes of variables) on arbitrary ground fields. In this general setting, in §1.1, we introduce still another residue, that we call additive residue. For a germ f as above, this is just defined as
This residue fails to be invariant under conjugacy; however, it has the (somewhat surprising and) very nice property of being a group homomorphism when restricted to the subgroup of parabolic germs having order of contact to the identity at least
![]() $\ell $
. Using this, in §1.2, we give a very short and conceptual proof of the important iterative formula for
$\ell $
. Using this, in §1.2, we give a very short and conceptual proof of the important iterative formula for
![]() $\mathrm {Resit}$
first established by Écalle: for
$\mathrm {Resit}$
first established by Écalle: for
![]() $n \neq 0$
,
$n \neq 0$
,
 $$ \begin{align*}\mathrm{Resit}(f^n) = \frac{\mathrm{Resit}(f)}{|n|}.\end{align*} $$
$$ \begin{align*}\mathrm{Resit}(f^n) = \frac{\mathrm{Resit}(f)}{|n|}.\end{align*} $$
An interesting relation with the classical Schwarzian derivative is presented in §1.3.
The definition of residues easily extends to germs of
![]() $C^{2\ell +1}$
diffeomorphisms that are exactly
$C^{2\ell +1}$
diffeomorphisms that are exactly
![]() $\ell $
-tangent to the identity (see §1.2). It is not hard to see that
$\ell $
-tangent to the identity (see §1.2). It is not hard to see that
![]() $\mathrm {Res}$
and
$\mathrm {Res}$
and
![]() $\mathrm {Resit}$
are invariant under conjugacy by
$\mathrm {Resit}$
are invariant under conjugacy by
![]() $C^{2\ell +1}$
diffeomorphisms. The first two main results of this work, stated and discussed in §2, establish that invariance actually holds for conjugacies by germs of
$C^{2\ell +1}$
diffeomorphisms. The first two main results of this work, stated and discussed in §2, establish that invariance actually holds for conjugacies by germs of
![]() $C^{\ell +1}$
diffeomorphisms and that this result is sharp.
$C^{\ell +1}$
diffeomorphisms and that this result is sharp.
Theorem A. Given
![]() $\ell \geq 1$
, let
$\ell \geq 1$
, let
![]() $f,g$
be two parabolic germs in
$f,g$
be two parabolic germs in
![]() $\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
$\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
![]() $\ell $
-tangent to the identity. If f and g are conjugated by a germ in
$\ell $
-tangent to the identity. If f and g are conjugated by a germ in
![]() $\mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
, then they have the same (iterative) residue.
$\mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
, then they have the same (iterative) residue.
Theorem B. Given
![]() $\ell \geq 1$
, let
$\ell \geq 1$
, let
![]() $f,g$
be two parabolic germs in
$f,g$
be two parabolic germs in
![]() $\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
$\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
![]() $\ell $
-tangent to the identity. If they are both expanding or both contracting, then they are conjugated by a germ in
$\ell $
-tangent to the identity. If they are both expanding or both contracting, then they are conjugated by a germ in
![]() $\mathrm {Diff}^{\, \ell }_+ (\mathbb {R},0)$
.
$\mathrm {Diff}^{\, \ell }_+ (\mathbb {R},0)$
.
Roughly, these results summarize (and are nicely complemented) as follows:
-
– Two nonflat parabolic germs of (real 1-D) diffeomorphisms are conjugate by the germ of (orientation-preserving)
 $C^1$
diffeomorphisms if and only if they have the same order of contact to the identity and the first (higher-order) nonzero coefficients of the Taylor series expansions have the same sign (this goes back to Firmo [Reference Firmo10]);
$C^1$
diffeomorphisms if and only if they have the same order of contact to the identity and the first (higher-order) nonzero coefficients of the Taylor series expansions have the same sign (this goes back to Firmo [Reference Firmo10]); -
– Any
 $C^1$
conjugacy is automatically of class
$C^1$
conjugacy is automatically of class
 $C^{\ell }$
if the order of tangency above is
$C^{\ell }$
if the order of tangency above is
 $\ell $
and the germs are of class
$\ell $
and the germs are of class
 $C^{2\ell + 1}$
;
$C^{2\ell + 1}$
; -
– An obstruction to improve the differentiability of the conjugacy above is given by the iterative residue: For
 $C^{2\ell + 1}$
diffeomorphisms that are exactly
$C^{2\ell + 1}$
diffeomorphisms that are exactly
 $\ell $
-tangent to the identity, this value is invariant under
$\ell $
-tangent to the identity, this value is invariant under
 $C^{\ell + 1}$
conjugacy.
$C^{\ell + 1}$
conjugacy.
After discussing some relevant examples and heuristic arguments in §2, a complete proof of Theorem A (resp. Theorem B) is presented in §3 (resp. §4). Actually, Theorem B is proved in the following extended form:
Theorem B’. Let
![]() $1 \leq r \leq \ell $
, and let
$1 \leq r \leq \ell $
, and let
![]() $f,g$
be two parabolic germs in
$f,g$
be two parabolic germs in
![]() $\mathrm {Diff}^{\ell + 1 + r}_+(\mathbb {R},0)$
that are exactly
$\mathrm {Diff}^{\ell + 1 + r}_+(\mathbb {R},0)$
that are exactly
![]() $\ell $
-tangent to the identity. If they are both expanding or both contracting, then they are conjugated by a germ in
$\ell $
-tangent to the identity. If they are both expanding or both contracting, then they are conjugated by a germ in
![]() $\mathrm {Diff}^{\, r}_+ (\mathbb {R},0)$
.
$\mathrm {Diff}^{\, r}_+ (\mathbb {R},0)$
.
To close this work, we study the regularity of the conjugacies in case of coincidence of residues. For germs of
![]() $C^{\infty }$
diffeomorphisms with the same order of tangency to the identity, Takens proved that they are
$C^{\infty }$
diffeomorphisms with the same order of tangency to the identity, Takens proved that they are
![]() $C^{\infty }$
conjugate provided they have the same iterative residue. Our last main result is a version of this phenomenon in finite regularity. Our proof strongly follows his arguments (and allows retrieving his result without using Borel’s lemma; see Remark 5.4).
$C^{\infty }$
conjugate provided they have the same iterative residue. Our last main result is a version of this phenomenon in finite regularity. Our proof strongly follows his arguments (and allows retrieving his result without using Borel’s lemma; see Remark 5.4).
Theorem C. Let
![]() $r \geq \ell + 1$
, and let
$r \geq \ell + 1$
, and let
![]() $f,g$
be germs of
$f,g$
be germs of
![]() $C^{\ell +1+r}$
diffeomorphisms, both expanding or both contracting, that are exactly
$C^{\ell +1+r}$
diffeomorphisms, both expanding or both contracting, that are exactly
![]() $\ell $
-tangent to the identity, with
$\ell $
-tangent to the identity, with
![]() $\ell \geq 1$
. If f and g have the same (iterative) residue, then they are
$\ell \geq 1$
. If f and g have the same (iterative) residue, then they are
![]() $C^{\ell +1}$
conjugate, and such a conjugacy is automatically a (germ of)
$C^{\ell +1}$
conjugate, and such a conjugacy is automatically a (germ of)
![]() $C^r$
diffeomorphism.
$C^r$
diffeomorphism.
In particular (take
![]() $r = \ell + 1$
), two germs of
$r = \ell + 1$
), two germs of
![]() $C^{2\ell + 2}$
diffeomorphisms with the same iterative residue that are both expanding or both contracting are
$C^{2\ell + 2}$
diffeomorphisms with the same iterative residue that are both expanding or both contracting are
![]() $C^{\ell +1}$
conjugate. Notice that this fails to be true for germs of
$C^{\ell +1}$
conjugate. Notice that this fails to be true for germs of
![]() $C^{2\ell +1}$
diffeomorphisms, as is shown by an example in §2.3.
$C^{2\ell +1}$
diffeomorphisms, as is shown by an example in §2.3.
This article is written in a pedagogic style because some of the issues discussed here are folklore. In particular, several sections presenting examples and alternative arguments may be skipped in a first reading by those who want to directly proceed to the core of the proofs. We hope that our presentation will help the readers in getting a panorama on the subject and will perhaps invite them to work on it. A couple of concrete questions on distortion elements of the group of germs of diffeomorphisms is addressed in the last section.
1 Some general (algebraic) facts
1.1 Germs and morphisms
Let
![]() $\mathbb {K}$
be an integral domain. We let
$\mathbb {K}$
be an integral domain. We let
![]() $\widehat {\mathrm {Diff}}(\mathbb {K},0)$
be the group of formal power series of the form
$\widehat {\mathrm {Diff}}(\mathbb {K},0)$
be the group of formal power series of the form
where
![]() $a_n \in \mathbb {K}$
and
$a_n \in \mathbb {K}$
and
![]() $a_1 \in \mathbb {K} \setminus \{0\}$
is invertible. The group operation is that of composition of series, which identifies to that of substitution of variables. In the case where
$a_1 \in \mathbb {K} \setminus \{0\}$
is invertible. The group operation is that of composition of series, which identifies to that of substitution of variables. In the case where
![]() $\mathbb {K}$
is a field, it also identifies to the group of formal germs of diffeomorphisms at the origin.
$\mathbb {K}$
is a field, it also identifies to the group of formal germs of diffeomorphisms at the origin.
For
![]() $\ell \geq 1$
, we consider the subgroup
$\ell \geq 1$
, we consider the subgroup
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
of
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
of
![]() $\widehat {\mathrm {Diff}}(\mathbb {K},0)$
formed by the germs that are
$\widehat {\mathrm {Diff}}(\mathbb {K},0)$
formed by the germs that are
![]() $\ell $
-tangent to the identity, that is, that are of the form
$\ell $
-tangent to the identity, that is, that are of the form
On
![]() $\widehat {\mathrm {Diff}}(\mathbb {K},0)$
, there is an obvious homomorphism
$\widehat {\mathrm {Diff}}(\mathbb {K},0)$
, there is an obvious homomorphism
![]() $\Phi _0$
into the multiplicative subgroup of the invertible elements of
$\Phi _0$
into the multiplicative subgroup of the invertible elements of
![]() $\mathbb {K} \setminus \{0\}$
given by
$\mathbb {K} \setminus \{0\}$
given by
Similarly, on each subgroup
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
, there is an obvious homomorphism
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
, there is an obvious homomorphism
![]() $\Phi _{\ell }$
into the additive group
$\Phi _{\ell }$
into the additive group
![]() $\mathbb {K}$
, namely,
$\mathbb {K}$
, namely,
Actually,
![]() $\Phi _{\ell }$
is the first of
$\Phi _{\ell }$
is the first of
![]() $\ell $
homomorphisms
$\ell $
homomorphisms
![]() $\Phi _{\ell ,1}, \Phi _{\ell ,2} \ldots , \Phi _{\ell ,\ell }$
defined on
$\Phi _{\ell ,1}, \Phi _{\ell ,2} \ldots , \Phi _{\ell ,\ell }$
defined on
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
by
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
by
(checking that these are homomorphisms is straightforward; see also (3) below).
Less trivially, there is another homomorphism from
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
into
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
into
![]() $\mathbb {K}$
, namely
$\mathbb {K}$
, namely
Whenever it makes sense (for instance, when
![]() $\mathbb {K}$
is a zero-characteristic field), we let
$\mathbb {K}$
is a zero-characteristic field), we let
 $$ \begin{align} \mathrm{Resad}_{\ell} \!: x + \sum_{n \geq \ell + 1} a_n x^n \mapsto \frac{\ell + 1}{2} \, a_{\ell + 1}^2 - a_{2\ell + 1}. \end{align} $$
$$ \begin{align} \mathrm{Resad}_{\ell} \!: x + \sum_{n \geq \ell + 1} a_n x^n \mapsto \frac{\ell + 1}{2} \, a_{\ell + 1}^2 - a_{2\ell + 1}. \end{align} $$
We call both
![]() $\overline {\mathrm {Resad}}_{\ell }$
and
$\overline {\mathrm {Resad}}_{\ell }$
and
![]() $\mathrm {Resad}_{\ell }$
the additive residues at order
$\mathrm {Resad}_{\ell }$
the additive residues at order
![]() $\ell + 1$
. Checking that they yield group homomorphisms is straightforward: If
$\ell + 1$
. Checking that they yield group homomorphisms is straightforward: If
then
![]() $fg(x)$
equals
$fg(x)$
equals
 $$ \begin{align*}\left[ x + \sum_{m \geq \ell + 1} a_m' x^m \right] + \sum_{n \geq \ell + 1} a_n \left[ x + \sum_{m \geq \ell + 1} a_m' x^m \right]^n,\end{align*} $$
$$ \begin{align*}\left[ x + \sum_{m \geq \ell + 1} a_m' x^m \right] + \sum_{n \geq \ell + 1} a_n \left[ x + \sum_{m \geq \ell + 1} a_m' x^m \right]^n,\end{align*} $$
that is,
 $$ \begin{align*}x + \sum_{m = \ell + 1}^{2\ell + 1} a_m' x^m + \sum_{n = \ell + 1}^{2\ell + 1} a_n x^n + a_{\ell + 1} (\ell + 1) x^{\ell} a_{\ell + 1}' x^{\ell + 1} + T_{2\ell+2},\end{align*} $$
$$ \begin{align*}x + \sum_{m = \ell + 1}^{2\ell + 1} a_m' x^m + \sum_{n = \ell + 1}^{2\ell + 1} a_n x^n + a_{\ell + 1} (\ell + 1) x^{\ell} a_{\ell + 1}' x^{\ell + 1} + T_{2\ell+2},\end{align*} $$
where
![]() $T_{2\ell +2}$
stands for a formal power series in x all of whose terms have order at least
$T_{2\ell +2}$
stands for a formal power series in x all of whose terms have order at least
![]() $2\ell +2$
. Therefore,
$2\ell +2$
. Therefore,
 $$ \begin{align} fg (x) = x + \sum_{n=\ell + 1}^{2 \ell} [a_n+a_n'] x^n + [a_{2\ell + 1} + a'_{2\ell + 1} + (\ell + 1) a_{\ell + 1} a_{\ell + 1}'] x^{2\ell + 1} + T_{2\ell+2}, \end{align} $$
$$ \begin{align} fg (x) = x + \sum_{n=\ell + 1}^{2 \ell} [a_n+a_n'] x^n + [a_{2\ell + 1} + a'_{2\ell + 1} + (\ell + 1) a_{\ell + 1} a_{\ell + 1}'] x^{2\ell + 1} + T_{2\ell+2}, \end{align} $$
and
 $$ \begin{align*}&\overline{\mathrm{Resad}}_{\ell} (fg) \\&\quad= (\ell + 1) \, [a_{\ell + 1} + a_{\ell + 1}']^2 - 2 \, [a_{2\ell + 1} + a'_{2\ell + 1} + (\ell + 1) a_{\ell + 1} a_{\ell + 1}'] = \overline{\mathrm{Resad}}_{\ell} (f) + \overline{\mathrm{Resad}}_{\ell} (g). \end{align*} $$
$$ \begin{align*}&\overline{\mathrm{Resad}}_{\ell} (fg) \\&\quad= (\ell + 1) \, [a_{\ell + 1} + a_{\ell + 1}']^2 - 2 \, [a_{2\ell + 1} + a'_{2\ell + 1} + (\ell + 1) a_{\ell + 1} a_{\ell + 1}'] = \overline{\mathrm{Resad}}_{\ell} (f) + \overline{\mathrm{Resad}}_{\ell} (g). \end{align*} $$
A basis for the cohomology. In the case where
![]() $\mathbb {K}$
is the field of real numbers, Fukui proved in [Reference Fukui5] that the
$\mathbb {K}$
is the field of real numbers, Fukui proved in [Reference Fukui5] that the
![]() $\Phi _{\ell ,i}$
together with
$\Phi _{\ell ,i}$
together with
![]() $\mathrm {Resad}_{\ell }$
are the generators of the continuous cohomology group of
$\mathrm {Resad}_{\ell }$
are the generators of the continuous cohomology group of
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
. In [Reference Babenko and Bogatyi1], Babenko and Bogatyi treated the case
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
. In [Reference Babenko and Bogatyi1], Babenko and Bogatyi treated the case
![]() $\mathbb {K} = \mathbb {Z}$
. In particular, they computed the continuous cohomology
$\mathbb {K} = \mathbb {Z}$
. In particular, they computed the continuous cohomology
![]() $H^1 (\widehat {\mathrm {Diff}}_1 (\mathbb {Z},0))$
: Besides
$H^1 (\widehat {\mathrm {Diff}}_1 (\mathbb {Z},0))$
: Besides
and
there are two homomorphisms into
![]() $\mathbb {Z}_2$
, namely
$\mathbb {Z}_2$
, namely
 $$ \begin{align*}x + \sum_{n \geq 2} a_n x^n \mapsto \frac{a_2 \, ( 1 + a_2 )}{2} + a_3 + a_4 \quad (\mbox{mod } 2)\end{align*} $$
$$ \begin{align*}x + \sum_{n \geq 2} a_n x^n \mapsto \frac{a_2 \, ( 1 + a_2 )}{2} + a_3 + a_4 \quad (\mbox{mod } 2)\end{align*} $$
and
In [Reference Bogatayaa and Bogatyi2], Bogatayaa and Bogatyi do similar computations for
![]() $\mathbb {K} = \mathbb {Z}_p$
, with p a prime number. They show that, for
$\mathbb {K} = \mathbb {Z}_p$
, with p a prime number. They show that, for
![]() $p \neq 2$
, only
$p \neq 2$
, only
![]() $\Phi _{1}$
and
$\Phi _{1}$
and
![]() $\mathrm {Resad}_1$
survive, but for
$\mathrm {Resad}_1$
survive, but for
![]() $p=2$
, the situation is slightly more complicated. See also [Reference Pavez17], where among other things it is shown that
$p=2$
, the situation is slightly more complicated. See also [Reference Pavez17], where among other things it is shown that
![]() $H^1 ( \widehat {\mathrm {Diff}}_{\ell }(\mathbb {Z},0))$
is finitely generated for all values of
$H^1 ( \widehat {\mathrm {Diff}}_{\ell }(\mathbb {Z},0))$
is finitely generated for all values of
![]() $\ell $
larger than
$\ell $
larger than
![]() $1$
.
$1$
.
Genuine diffeomorphisms. For
![]() $\mathbb {K}$
being the fields of the real, complex or p-adic numbers, we let
$\mathbb {K}$
being the fields of the real, complex or p-adic numbers, we let
![]() $\mathrm {Diff}^{\omega } (\mathbb {K},0)$
be the group of genuine germs of analytic diffeomorphisms fixing the origin, and
$\mathrm {Diff}^{\omega } (\mathbb {K},0)$
be the group of genuine germs of analytic diffeomorphisms fixing the origin, and
![]() $\mathrm {Diff}^{\omega }_{\ell } (\mathbb {K},0)$
the subgroup of those elements that are
$\mathrm {Diff}^{\omega }_{\ell } (\mathbb {K},0)$
the subgroup of those elements that are
![]() $\ell $
-tangent to the identity. These are subgroups of the corresponding groups
$\ell $
-tangent to the identity. These are subgroups of the corresponding groups
![]() $\widehat {\mathrm {Diff}}(\mathbb {K},0)$
and
$\widehat {\mathrm {Diff}}(\mathbb {K},0)$
and
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
, so the homomorphisms
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
, so the homomorphisms
![]() $\Phi _{\ell ,i}$
and
$\Phi _{\ell ,i}$
and
![]() $\mathrm {Resad}_{\ell }$
restrict to them.
$\mathrm {Resad}_{\ell }$
restrict to them.
More interestingly, each of the homomorphisms
![]() $\Phi _{\ell ,i}$
and
$\Phi _{\ell ,i}$
and
![]() $\mathrm {Resad}_{\ell }$
above involve only finitely many derivatives at the origin (namely,
$\mathrm {Resad}_{\ell }$
above involve only finitely many derivatives at the origin (namely,
![]() $\ell + i$
and
$\ell + i$
and
![]() $2\ell + 1$
, respectively). Their definitions hence extend to the subgroup
$2\ell + 1$
, respectively). Their definitions hence extend to the subgroup
![]() $\mathrm {Diff}^{\infty }_{\ell } (\mathbb {K},0)$
of the group
$\mathrm {Diff}^{\infty }_{\ell } (\mathbb {K},0)$
of the group
![]() $\mathrm {Diff}^{\infty } (\mathbb {K},0)$
of germs of
$\mathrm {Diff}^{\infty } (\mathbb {K},0)$
of germs of
![]() $C^{\infty }$
diffeomorphisms fixing the origin made of the elements that are
$C^{\infty }$
diffeomorphisms fixing the origin made of the elements that are
![]() $\ell $
-tangent to the identity. Actually, they even extend to the larger group of germs of
$\ell $
-tangent to the identity. Actually, they even extend to the larger group of germs of
![]() $C^{2\ell + 1}$
diffeomorphisms that are
$C^{2\ell + 1}$
diffeomorphisms that are
![]() $\ell $
-tangent to the identity. In this framework, it is a nice exercise to check the additive property of
$\ell $
-tangent to the identity. In this framework, it is a nice exercise to check the additive property of
![]() $\mathrm {Resad}_{\ell }$
just by using the Faà di Bruno formula. We will come back to this point in §1.3.
$\mathrm {Resad}_{\ell }$
just by using the Faà di Bruno formula. We will come back to this point in §1.3.
Fukui’s theorem stated above still holds in
![]() $\mathrm {Diff}^{\infty }_+ (\mathbb {R},0)$
(where
$\mathrm {Diff}^{\infty }_+ (\mathbb {R},0)$
(where
![]() $+$
stands for orientation-preserving maps). We do not know whether a complex or p-adic version of this is also valid.
$+$
stands for orientation-preserving maps). We do not know whether a complex or p-adic version of this is also valid.
1.2 Res-it-ad
Elements in
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
are those whose order of contact to the identity at the origin equals
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
are those whose order of contact to the identity at the origin equals
![]() $\ell $
. For simplicity, they will be said to be exactly
$\ell $
. For simplicity, they will be said to be exactly
![]() $\ell $
-tangent to the identity. These correspond to series expansions of the form
$\ell $
-tangent to the identity. These correspond to series expansions of the form
A well-known lemma gives a normal form for these elements.
Lemma 1.1. If
![]() $\mathbb {K}$
is a zero-characteristic field having a square root of
$\mathbb {K}$
is a zero-characteristic field having a square root of
![]() $-1$
, then every
$-1$
, then every
![]() $f~\in ~\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
is conjugate in
$f~\in ~\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
is conjugate in
![]() $\widehat {\mathrm {Diff}} (\mathbb {K},0)$
to a (unique) germ of the (normal) form
$\widehat {\mathrm {Diff}} (\mathbb {K},0)$
to a (unique) germ of the (normal) form
An explicit argument showing this in the complex case that applies with no modification to the present case appears in [Reference Voronin22]. The value of
![]() $\mu $
is called the residue of f and denoted
$\mu $
is called the residue of f and denoted
![]() $\mathrm {Res} (f)$
. As it is very well known (and easy to check), this is invariant under conjugacy. Actually, if f with normal form (4) is conjugate in
$\mathrm {Res} (f)$
. As it is very well known (and easy to check), this is invariant under conjugacy. Actually, if f with normal form (4) is conjugate in
![]() $\widehat {\mathrm {Diff}}(\mathbb {K},0)$
to a germ of the (reduced) form
$\widehat {\mathrm {Diff}}(\mathbb {K},0)$
to a germ of the (reduced) form
then necessarily
![]() $a_{2\ell + 1} = \mathrm {Res} (f)$
.
$a_{2\ell + 1} = \mathrm {Res} (f)$
.
The residue was introduced as a conjugacy invariant in the complex setting: For a germ of a holomorphic map fixing the origin, one defines
 $$ \begin{align*}\mathrm{R}(f) := \frac{1}{2 \pi i} \int_{\gamma} \frac{dz}{z - f(z)},\end{align*} $$
$$ \begin{align*}\mathrm{R}(f) := \frac{1}{2 \pi i} \int_{\gamma} \frac{dz}{z - f(z)},\end{align*} $$
where
![]() $\gamma $
is a small, simple and positively oriented loop around the origin. For germs of the form
$\gamma $
is a small, simple and positively oriented loop around the origin. For germs of the form
one easily checks that
![]() $\mathrm {R}(f) = \mathrm {Res} (f) = a_{2\ell +1}$
.
$\mathrm {R}(f) = \mathrm {Res} (f) = a_{2\ell +1}$
.
The iterative residue of
![]() $f \in \widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
, denoted
$f \in \widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
, denoted
![]() $\mathrm {Resit} (f)$
, is simply the value
$\mathrm {Resit} (f)$
, is simply the value
This satisfies the fundamental relation
 $$ \begin{align} \mathrm{Resit} (f^n) = \frac{\mathrm{Resit}(f)}{|n|} \end{align} $$
$$ \begin{align} \mathrm{Resit} (f^n) = \frac{\mathrm{Resit}(f)}{|n|} \end{align} $$
for every integer
![]() $n \neq 0$
. It was introduced by Écalle in the context of germs of holomorphic diffeomorphisms [Reference Écalle6]. A proof of the formula above in this setting (due to Écalle) appears for instance in [Reference Milnor13]. Below, we give an algebraic proof that works in a much broader context (in particular, it covers the case of germs of diffeomorphisms of the real line with finite regularity discussed just after Lemma 1.3). As we will see, it just follows from the additive properties of
$n \neq 0$
. It was introduced by Écalle in the context of germs of holomorphic diffeomorphisms [Reference Écalle6]. A proof of the formula above in this setting (due to Écalle) appears for instance in [Reference Milnor13]. Below, we give an algebraic proof that works in a much broader context (in particular, it covers the case of germs of diffeomorphisms of the real line with finite regularity discussed just after Lemma 1.3). As we will see, it just follows from the additive properties of
![]() $\Phi _{\ell }$
and
$\Phi _{\ell }$
and
![]() $\mathrm {Resad}_{\ell }$
.
$\mathrm {Resad}_{\ell }$
.
Start with a germ of the form
Using the homomorphisms
![]() $\Phi _{\ell }$
and
$\Phi _{\ell }$
and
![]() $\mathrm {Resad}_{\ell }$
, we obtain
$\mathrm {Resad}_{\ell }$
, we obtain
with
 $$ \begin{align*}\frac{(\ell + 1) \, n^2}{2} - \mu_n = \mathrm{Resad}_{\ell} (f^n) = n \, \mathrm{Resad}_{\ell} (f) = n \, \left[ \frac{(\ell + 1)}{2} - \mu \right] = n \, \mathrm{Resit}(f).\end{align*} $$
$$ \begin{align*}\frac{(\ell + 1) \, n^2}{2} - \mu_n = \mathrm{Resad}_{\ell} (f^n) = n \, \mathrm{Resad}_{\ell} (f) = n \, \left[ \frac{(\ell + 1)}{2} - \mu \right] = n \, \mathrm{Resit}(f).\end{align*} $$
Assume
![]() $n> 0$
. If we conjugate by
$n> 0$
. If we conjugate by
![]() $H_{\lambda _n} \! : x \mapsto \lambda x$
with
$H_{\lambda _n} \! : x \mapsto \lambda x$
with
![]() $\lambda _n := \sqrt [\ell ]{n}$
, we obtain
$\lambda _n := \sqrt [\ell ]{n}$
, we obtain
By definition, this implies that
 $$ \begin{align*}\mathrm{Resit} (f^n) = \frac{\ell + 1}{2} - \frac{\mu_n}{n^2} = \frac{1}{n^2} \left[ \frac{(\ell + 1) \, n^2}{2} - \mu_n \right] = \frac{ n \, \mathrm{Resit} (f) }{n^2} = \frac{\mathrm{Resit}(f)}{n}\end{align*} $$
$$ \begin{align*}\mathrm{Resit} (f^n) = \frac{\ell + 1}{2} - \frac{\mu_n}{n^2} = \frac{1}{n^2} \left[ \frac{(\ell + 1) \, n^2}{2} - \mu_n \right] = \frac{ n \, \mathrm{Resit} (f) }{n^2} = \frac{\mathrm{Resit}(f)}{n}\end{align*} $$
as announced. Computations for
![]() $n < 0$
are analogous.
$n < 0$
are analogous.
Example 1.2. It follows from (the proof of) Lemma 1.1 (see also Lemma 1.3 below) that, for
![]() $f \in \widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
of the form
$f \in \widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0) \setminus \widehat {\mathrm {Diff}}_{\ell + 1}(\mathbb {K},0)$
of the form
the value of
![]() $\mathrm {Resit} (f)$
is a polynomial function of
$\mathrm {Resit} (f)$
is a polynomial function of
![]() $a_{\ell + 1},a_{\ell +2}, \ldots , a_{2\ell + 1}$
times some integer power of
$a_{\ell + 1},a_{\ell +2}, \ldots , a_{2\ell + 1}$
times some integer power of
![]() $a_{\ell + 1}$
. For instance, the reader may readily check that, for
$a_{\ell + 1}$
. For instance, the reader may readily check that, for
![]() $a \neq 0$
,
$a \neq 0$
,
See [Reference Nordqvist and Rivera-Letelier16, Theorem 1] for a general result in this direction.
The residues in the real case. Much of the discussion above still makes sense for germs of
![]() $C^{2\ell + 1}$
diffeomorphisms. In particular, the morphisms
$C^{2\ell + 1}$
diffeomorphisms. In particular, the morphisms
![]() $\Phi _{\ell ,i}$
and
$\Phi _{\ell ,i}$
and
![]() $\mathrm {Resad}_{\ell }$
extend to the subgroup
$\mathrm {Resad}_{\ell }$
extend to the subgroup
![]() $\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0)$
made of those germs that are
$\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0)$
made of those germs that are
![]() $\ell $
-tangent to the identity. Moreover, the definition of
$\ell $
-tangent to the identity. Moreover, the definition of
![]() $\mathrm {Resit}$
still extends to the elements of this subgroup that are exactly
$\mathrm {Resit}$
still extends to the elements of this subgroup that are exactly
![]() $\ell $
-tangent to the identity at the origin because of the next very well-known lemma. (Compare Lemma 1.1.) For the statement, recall that a germ f of diffeomorphisms of the real line fixing the origin is (topologically) contracting (resp. expanding) if
$\ell $
-tangent to the identity at the origin because of the next very well-known lemma. (Compare Lemma 1.1.) For the statement, recall that a germ f of diffeomorphisms of the real line fixing the origin is (topologically) contracting (resp. expanding) if
![]() $f(x) < x$
(resp.
$f(x) < x$
(resp.
![]() $f(x)>x$
) holds for all small-enough
$f(x)>x$
) holds for all small-enough
![]() $x>0$
. In all that follows, the little-o-notation
$x>0$
. In all that follows, the little-o-notation
![]() $o (\cdot )$
will refer to values of the involved variable that are positive but very close to zero.
$o (\cdot )$
will refer to values of the involved variable that are positive but very close to zero.
Lemma 1.3. Let f be the germ of a
![]() $C^{2\ell + 1}$
diffeomorphism of the real line that is exactly
$C^{2\ell + 1}$
diffeomorphism of the real line that is exactly
![]() $\ell $
-tangent to the identity at the origin. If f is expanding (resp. contracting), then there exists a germ of polynomial diffeomorphism h such that the conjugate germ
$\ell $
-tangent to the identity at the origin. If f is expanding (resp. contracting), then there exists a germ of polynomial diffeomorphism h such that the conjugate germ
![]() $hfh^{-1}$
has a Taylor series expansion at the origin of the (reduced) form
$hfh^{-1}$
has a Taylor series expansion at the origin of the (reduced) form
where the sign is positive (resp. negative) in the expanding (resp. contracting) case. Moreover,
![]() $\mu $
is uniquely determined up to conjugacy by a germ of
$\mu $
is uniquely determined up to conjugacy by a germ of
![]() $C^{2\ell + 1}$
diffeomorphism.
$C^{2\ell + 1}$
diffeomorphism.
Proof. By assumption, f has a Taylor series expansion at the origin of the form
 $$ \begin{align*}f(x) = x + \sum_{n=\ell + 1}^{2\ell + 1} a_n x^n + o (x^{2\ell + 1}), \quad \mbox{with } a_{\ell + 1} \neq 0.\end{align*} $$
$$ \begin{align*}f(x) = x + \sum_{n=\ell + 1}^{2\ell + 1} a_n x^n + o (x^{2\ell + 1}), \quad \mbox{with } a_{\ell + 1} \neq 0.\end{align*} $$
By conjugating f by a homothety, we can arrange that
![]() $a_{\ell + 1} = 1$
(resp.
$a_{\ell + 1} = 1$
(resp.
![]() $a_{\ell + 1} = -1$
) in the expanding (resp. contracting) case. Now, by conjugating by a germ of the form
$a_{\ell + 1} = -1$
) in the expanding (resp. contracting) case. Now, by conjugating by a germ of the form
![]() $x+\alpha x^2$
, we can make
$x+\alpha x^2$
, we can make
![]() $a_{\ell +2}$
vanish without changing
$a_{\ell +2}$
vanish without changing
![]() $a_{\ell + 1} = \pm 1$
. Next, we conjugate by a germ of the form
$a_{\ell + 1} = \pm 1$
. Next, we conjugate by a germ of the form
![]() $x+\alpha x^3$
to make
$x+\alpha x^3$
to make
![]() $a_{\ell +3}$
vanish without changing
$a_{\ell +3}$
vanish without changing
![]() $a_{\ell + 1} = \pm 1$
and
$a_{\ell + 1} = \pm 1$
and
![]() $a_{\ell +2}=0$
. One continues this way up to conjugating by a germ of the form
$a_{\ell +2}=0$
. One continues this way up to conjugating by a germ of the form
![]() $x+\alpha x^{\ell }$
, which allows killing
$x+\alpha x^{\ell }$
, which allows killing
![]() $a_{2\ell }$
. We leave it to the reader to fill in the details as well as the proof of the uniqueness of
$a_{2\ell }$
. We leave it to the reader to fill in the details as well as the proof of the uniqueness of
![]() $\mu $
(see also [Reference Voronin22]).
$\mu $
(see also [Reference Voronin22]).
In any case above, we let
One readily checks that this definition is coherent with that of the complex analytic case.
Remark 1.4. Strictly speaking, for a germ of diffeomorphism that is
![]() $\ell $
-tangent to the identity, one does not need
$\ell $
-tangent to the identity, one does not need
![]() $C^{2\ell +1}$
regularity to define residues:
$C^{2\ell +1}$
regularity to define residues:
![]() $(2\ell + 1)$
-differentiability at the origin is enough. Indeed, all definitions only use Taylor series expansions at the origin and their algebraic properties under composition.
$(2\ell + 1)$
-differentiability at the origin is enough. Indeed, all definitions only use Taylor series expansions at the origin and their algebraic properties under composition.
1.3 Schwarzian derivatives and
 $\mathbf {Resad}_{\boldsymbol{\ell} }$
$\mathbf {Resad}_{\boldsymbol{\ell} }$
For a germ of a genuine diffeomorphism
![]() $f \in \mathrm {Diff}^{\infty }(\mathbb {K},0)$
(where
$f \in \mathrm {Diff}^{\infty }(\mathbb {K},0)$
(where
![]() $\mathbb {K}$
is, for example, the field of real numbers), one has
$\mathbb {K}$
is, for example, the field of real numbers), one has
Thus, if
![]() $Df (0) = 1$
, then
$Df (0) = 1$
, then
 $$ \begin{align*}\mathrm{Resad}_1 (f) = a_2^2 - a_3 = \frac{(D^2 f (0))^2}{4} - \frac{D^3f(0)}{6} = \frac{1}{6} \left[ \frac{3}{2} \left( \frac{D^2 f(0)}{Df(0)} \right)^2 - \frac{D^3f (0)}{Df(0)} \right] = \frac{Sf (0)}{6},\end{align*} $$
$$ \begin{align*}\mathrm{Resad}_1 (f) = a_2^2 - a_3 = \frac{(D^2 f (0))^2}{4} - \frac{D^3f(0)}{6} = \frac{1}{6} \left[ \frac{3}{2} \left( \frac{D^2 f(0)}{Df(0)} \right)^2 - \frac{D^3f (0)}{Df(0)} \right] = \frac{Sf (0)}{6},\end{align*} $$
where
![]() $Sf$
denotes the Schwarzian derivative. That
$Sf$
denotes the Schwarzian derivative. That
![]() $Sf$
appears as a group homomorphism is not surprising. Indeed, in a general setting, it satisfies the cocycle identity
$Sf$
appears as a group homomorphism is not surprising. Indeed, in a general setting, it satisfies the cocycle identity
and restricted to parabolic germs, this becomes
In this view,
![]() $\mathrm {Resad}_{\ell }$
may be seen as a kind of ‘Schwarzian derivative of higher order’ for parabolic germs. Now, for
$\mathrm {Resad}_{\ell }$
may be seen as a kind of ‘Schwarzian derivative of higher order’ for parabolic germs. Now, for
![]() $f \in \mathrm {Diff}_{\ell }^{\infty } (\mathbb {K},0)$
, we have
$f \in \mathrm {Diff}_{\ell }^{\infty } (\mathbb {K},0)$
, we have
 $$ \begin{align*}&\mathrm{Resad}_{\ell} (f) \\&\quad= \frac{\ell + 1}{2} \left( \frac{D^i f (0)}{(\ell + 1)\,!} \right)^2 - \frac{D^{2\ell + 1}f(0)}{(2\ell + 1)\,!} = \frac{1}{(2\ell + 1)\, !} \left[ {2\ell + 1 \choose \ell} \frac{(D^{\ell + 1} f(0))^2}{2} - D^{2\ell + 1} f (0) \right] \! .\end{align*} $$
$$ \begin{align*}&\mathrm{Resad}_{\ell} (f) \\&\quad= \frac{\ell + 1}{2} \left( \frac{D^i f (0)}{(\ell + 1)\,!} \right)^2 - \frac{D^{2\ell + 1}f(0)}{(2\ell + 1)\,!} = \frac{1}{(2\ell + 1)\, !} \left[ {2\ell + 1 \choose \ell} \frac{(D^{\ell + 1} f(0))^2}{2} - D^{2\ell + 1} f (0) \right] \! .\end{align*} $$
Thus, letting
 $$ \begin{align*}S_{\ell + 1} (f) := {2\ell + 1 \choose \ell} \frac{(D^{\ell + 1} f(0))^2}{2} - D^{2\ell + 1} f (0) = (2\ell+1)! \, \mathrm{Resad}_{\ell}(f),\end{align*} $$
$$ \begin{align*}S_{\ell + 1} (f) := {2\ell + 1 \choose \ell} \frac{(D^{\ell + 1} f(0))^2}{2} - D^{2\ell + 1} f (0) = (2\ell+1)! \, \mathrm{Resad}_{\ell}(f),\end{align*} $$
we have
![]() $S_1 (f) = S(f)$
.
$S_1 (f) = S(f)$
.
In a slightly broader context, if
![]() $f,g$
are two germs of
$f,g$
are two germs of
![]() $C^{2\ell + 1}$
diffeomorphisms with all derivatives
$C^{2\ell + 1}$
diffeomorphisms with all derivatives
![]() $D^2, D^3, \ldots ,D^{\ell }$
vanishing at the origin, then, using the Faà di Bruno formula, it is straightforward to check the cocycle relation below:
$D^2, D^3, \ldots ,D^{\ell }$
vanishing at the origin, then, using the Faà di Bruno formula, it is straightforward to check the cocycle relation below:
This is an extension of the additive property of
![]() $\mathrm {Resad}_{\ell }$
to the framework of nonparabolic germs.
$\mathrm {Resad}_{\ell }$
to the framework of nonparabolic germs.
Remark 1.5. A classical theorem of Szekeres establishes that every expanding or contracting germ of
![]() $C^2$
diffeomorphism of the real line is the time-1 map of a flow of germs of
$C^2$
diffeomorphism of the real line is the time-1 map of a flow of germs of
![]() $C^1$
diffeomorphisms; moreover, a famous lemma of Kopell establishes that its centralizer in the group of germs of
$C^1$
diffeomorphisms; moreover, a famous lemma of Kopell establishes that its centralizer in the group of germs of
![]() $C^1$
diffeomorphisms coincides with this flow (see [Reference Navas15, chapter 4]). Furthermore, it follows from the work of Yoccoz [Reference Yoccoz23] that, for nonflat germs of class
$C^1$
diffeomorphisms coincides with this flow (see [Reference Navas15, chapter 4]). Furthermore, it follows from the work of Yoccoz [Reference Yoccoz23] that, for nonflat germs of class
![]() $C^k$
, the flow is made of
$C^k$
, the flow is made of
![]() $C^{k-1}$
diffeomorphisms. Therefore, to each
$C^{k-1}$
diffeomorphisms. Therefore, to each
![]() $f \in \mathrm {Diff}^{2\ell + 2}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 2}_{\ell +1} (\mathbb {R},0)$
we may associate its flow
$f \in \mathrm {Diff}^{2\ell + 2}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 2}_{\ell +1} (\mathbb {R},0)$
we may associate its flow
![]() $(f^t)$
made of
$(f^t)$
made of
![]() $C^{2\ell +1}$
germs of diffeomorphisms. These are easily seen to be exactly
$C^{2\ell +1}$
germs of diffeomorphisms. These are easily seen to be exactly
![]() $\ell $
-flat. Moreover, equality (5) has a natural extension in this setting, namely, for all
$\ell $
-flat. Moreover, equality (5) has a natural extension in this setting, namely, for all
![]() $t \neq 0$
,
$t \neq 0$
,
 $$ \begin{align} \mathrm{Resit}(f^t) = \frac{\mathrm{Resit}(f)}{|t|}. \end{align} $$
$$ \begin{align} \mathrm{Resit}(f^t) = \frac{\mathrm{Resit}(f)}{|t|}. \end{align} $$
See Remark 3.1 for a proof.
Remark 1.6. In the real or complex setting, if
then, letting
![]() $h (x) = x^{\ell }$
, one readily checks that
$h (x) = x^{\ell }$
, one readily checks that
 $$ \begin{align} h f h^{-1} (x) = x + \ell \, a \, x^2 + \left[ \ell \, b + \frac{ \ell \, (\ell-1)}{2} a^2 \right] x^3 + \ldots. \end{align} $$
$$ \begin{align} h f h^{-1} (x) = x + \ell \, a \, x^2 + \left[ \ell \, b + \frac{ \ell \, (\ell-1)}{2} a^2 \right] x^3 + \ldots. \end{align} $$
Moreover, using Lemmas 4.4 and 4.5 below, one can show that
![]() $hfh^{-1}$
is of class
$hfh^{-1}$
is of class
![]() $C^3$
if f is of class
$C^3$
if f is of class
![]() $C^{2\ell +1}$
(yet this is not crucial to define residues, according to Remark 1.4). Now, Equation (8) easily yields
$C^{2\ell +1}$
(yet this is not crucial to define residues, according to Remark 1.4). Now, Equation (8) easily yields
The value of
![]() $\mathrm {Resad}_{\ell }$
hence equals (up to a constant) that of
$\mathrm {Resad}_{\ell }$
hence equals (up to a constant) that of
![]() $\mathrm {Resad}_1$
of the conjugate, and the same holds for
$\mathrm {Resad}_1$
of the conjugate, and the same holds for
![]() $\mathrm {Resit}$
. Since
$\mathrm {Resit}$
. Since
![]() $\mathrm {Resad}_1$
is nothing but a sixth of the Schwarzian derivative, this gives even more insight on
$\mathrm {Resad}_1$
is nothing but a sixth of the Schwarzian derivative, this gives even more insight on
![]() $\mathrm {Resad}_{\ell }$
as a generalization of the Schwarzian derivative. Compare [Reference Burslem and Wilkinson3], where the Schwarzian derivative naturally arises in the study of conjugacy classes of germs of real-analytic diffeomorphisms.
$\mathrm {Resad}_{\ell }$
as a generalization of the Schwarzian derivative. Compare [Reference Burslem and Wilkinson3], where the Schwarzian derivative naturally arises in the study of conjugacy classes of germs of real-analytic diffeomorphisms.
2 On conjugacies and residues: statements, examples
Let us next recall the first two main results of this work.
Theorem A. Given
![]() $\ell \geq 1$
, let
$\ell \geq 1$
, let
![]() $f,g$
be two parabolic germs in
$f,g$
be two parabolic germs in
![]() $\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
$\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
![]() $\ell $
-tangent to the identity. If f and g are conjugated by a germ in
$\ell $
-tangent to the identity. If f and g are conjugated by a germ in
![]() $\mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
, then they have the same (iterative) residue.
$\mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
, then they have the same (iterative) residue.
Theorem B. Given
![]() $\ell \geq 1$
, let
$\ell \geq 1$
, let
![]() $f,g$
be two parabolic germs in
$f,g$
be two parabolic germs in
![]() $\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
$\mathrm {Diff}^{2\ell + 1}_+(\mathbb {R},0)$
that are exactly
![]() $\ell $
-tangent to the identity. If they are both expanding or both contracting, then they are conjugated by a germ in
$\ell $
-tangent to the identity. If they are both expanding or both contracting, then they are conjugated by a germ in
![]() $\mathrm {Diff}^{\, \ell }_+ (\mathbb {R},0)$
.
$\mathrm {Diff}^{\, \ell }_+ (\mathbb {R},0)$
.
In §3, we will give two complete and somewhat independent proofs of Theorem A. A proof of Theorem B (in the extended form given by Theorem B’ from the Introduction) will be presented in §4. Here, we illustrate both of them with several clarifying examples; in particular, in §2.3, we give an example that shows that the converse of Theorem A does not hold. The reader interested in proofs may skip most of this (somewhat long) section.
2.1 A fundamental example: (non-)invariance of residues
Let us consider the germs of
These have different residues:
Using that
![]() $\Phi _{1}(f) = \Phi _{1} (g)$
, one easily concludes that any
$\Phi _{1}(f) = \Phi _{1} (g)$
, one easily concludes that any
![]() $C^2$
conjugacy between f and g has to be parabolic (see the first proof below). Now, because of the invariance of
$C^2$
conjugacy between f and g has to be parabolic (see the first proof below). Now, because of the invariance of
![]() $\mathrm {Resad}_1$
(equivalently, of the Schwarzian derivative) under conjugacies by parabolic germs of
$\mathrm {Resad}_1$
(equivalently, of the Schwarzian derivative) under conjugacies by parabolic germs of
![]() $C^3$
diffeomorphisms, we conclude that no
$C^3$
diffeomorphisms, we conclude that no
![]() $C^3$
conjugacy between them can exist. However, Theorems A and B above imply that, actually, these germs are not
$C^3$
conjugacy between them can exist. However, Theorems A and B above imply that, actually, these germs are not
![]() $C^2$
conjugate, though they are
$C^2$
conjugate, though they are
![]() $C^1$
conjugate. Below, we elaborate on these two claims. We do this in two different ways: the former by directly looking at the conjugacy relation and the latter by looking at the associated vector fields.
$C^1$
conjugate. Below, we elaborate on these two claims. We do this in two different ways: the former by directly looking at the conjugacy relation and the latter by looking at the associated vector fields.
Proof Sketch of proof that
 $f,\,g$
are not
$f,\,g$
are not
 $C^2$
conjugate.
$C^2$
conjugate.
Assume that h is a germ of
![]() $C^2$
diffeomorphism conjugating f and g, that is,
$C^2$
diffeomorphism conjugating f and g, that is,
![]() $hfh^{-1} = g$
. Writing
$hfh^{-1} = g$
. Writing
![]() $h(x) = \lambda \, x + a x^2 + o(x^2)$
for
$h(x) = \lambda \, x + a x^2 + o(x^2)$
for
![]() $\lambda = Dh (0) \neq 0$
and
$\lambda = Dh (0) \neq 0$
and
![]() $a = D^2h(0)/2$
, equality
$a = D^2h(0)/2$
, equality
![]() $hf = gh$
translates to
$hf = gh$
translates to
Thus,
By identifying the coefficients of
![]() $x^2$
, this yields
$x^2$
, this yields
hence
![]() $\lambda = \lambda ^2$
and, therefore,
$\lambda = \lambda ^2$
and, therefore,
![]() $\lambda = 1$
.
$\lambda = 1$
.
Now, knowing that
![]() $Dh(0)=1$
, we deduce that there exists
$Dh(0)=1$
, we deduce that there exists
![]() $C> 0$
such that
$C> 0$
such that
for small-enough
![]() $x> 0$
. Now, notice that
$x> 0$
. Now, notice that
![]() $g^n (x) = \frac {x}{1+nx}.$
In particular, given any fixed
$g^n (x) = \frac {x}{1+nx}.$
In particular, given any fixed
![]() $x_0'> 0$
,
$x_0'> 0$
,
for a very large
![]() $D> 0$
(namely, for
$D> 0$
(namely, for
![]() $D \geq 1/x_0'$
) and all
$D \geq 1/x_0'$
) and all
![]() $n \geq 1$
. In what concerns f, a straightforward induction argument (that we leave to the reader; see also Proposition 3.2) shows that, for all
$n \geq 1$
. In what concerns f, a straightforward induction argument (that we leave to the reader; see also Proposition 3.2) shows that, for all
![]() $x_0> 0$
, there exists a (very small) constant
$x_0> 0$
, there exists a (very small) constant
![]() $D'> 0$
such that, for all
$D'> 0$
such that, for all
![]() $n \geq 1$
,
$n \geq 1$
,
Now, fix
![]() $x_0> 0$
, and let
$x_0> 0$
, and let
![]() $x_0' := h (x_0)$
. The equality
$x_0' := h (x_0)$
. The equality
![]() $hf^n (x_0) = g^n h(x_0)$
then yields
$hf^n (x_0) = g^n h(x_0)$
then yields
Using (9), (10) and (11), we obtain
 $$ \begin{align*}\frac{C}{(n+D'\log(n))^2} \geq C (f^n(x_0))^2 \geq \frac{1}{n+D} - \frac{1}{n + D' \log (n)} = \frac{D' \log (n) - D}{ (n+D) (n + D' \log (n))},\end{align*} $$
$$ \begin{align*}\frac{C}{(n+D'\log(n))^2} \geq C (f^n(x_0))^2 \geq \frac{1}{n+D} - \frac{1}{n + D' \log (n)} = \frac{D' \log (n) - D}{ (n+D) (n + D' \log (n))},\end{align*} $$
which is impossible for a large-enough n.
Proof Sketch of proof that
 $f,\,g$
are
$f,\,g$
are
 $C^1$
conjugate.
$C^1$
conjugate.
The existence of a
![]() $C^1$
conjugacy between diffeomorphisms as f and g above is folklore (see, for instance, [Reference O’Farrell and Roginskaya9, Reference Firmo10]). An argument that goes back to Szekeres [Reference Szekeres20] and Sergeraert [Reference Sergeraert19] proceeds as follows: The equality
$C^1$
conjugacy between diffeomorphisms as f and g above is folklore (see, for instance, [Reference O’Farrell and Roginskaya9, Reference Firmo10]). An argument that goes back to Szekeres [Reference Szekeres20] and Sergeraert [Reference Sergeraert19] proceeds as follows: The equality
![]() $hfh^{-1} = g$
implies
$hfh^{-1} = g$
implies
![]() $hf^nh^{-1} = g^n$
for all
$hf^nh^{-1} = g^n$
for all
![]() $n \geq 1$
, hence
$n \geq 1$
, hence
![]() $h = g^{-n} h f^n$
. Thus, if h is of class
$h = g^{-n} h f^n$
. Thus, if h is of class
![]() $C^1$
, then
$C^1$
, then
 $$ \begin{align} Dh (x) = \frac{Df^n (x)}{Dg^n (g^{-n} h f^n (x))} Dh (f^n (x)) = \frac{Df^n (x)}{Dg^n (h(x))} Dh (f^n (x)). \end{align} $$
$$ \begin{align} Dh (x) = \frac{Df^n (x)}{Dg^n (g^{-n} h f^n (x))} Dh (f^n (x)) = \frac{Df^n (x)}{Dg^n (h(x))} Dh (f^n (x)). \end{align} $$
It turns out that the sequence of functions
 $$ \begin{align*}(x,y) \to A_n (x,y) := \frac{Df^n (x)}{Dg^n (y)}\end{align*} $$
$$ \begin{align*}(x,y) \to A_n (x,y) := \frac{Df^n (x)}{Dg^n (y)}\end{align*} $$
is somewhat well behaved. In particular, it converges to a continuous function A away from the origin. Since
![]() $Dh(0)=1$
(see the proof above), Equation (12) translates to
$Dh(0)=1$
(see the proof above), Equation (12) translates to
This is an ordinary differential equation in h, a careful analysis of which shows that it has a solution. This allows one to obtain the conjugacy between f and g. See [Reference Firmo10] for the details.
It is worth stressing that both proofs above used not just the conjugacy relation but an iterated version of it:
In this regard, it may be clarifying for the reader to look for direct proofs just using the conjugacy relation in order to detect where things get stuck. The moral is that one really needs to use the underlying dynamics. Now, there are objects that encode such dynamics, namely, the vector fields whose time-1 maps correspond to the given diffeomorphisms. These were proved to exist by Szekeres [Reference Szekeres20] and Sergeraert [Reference Sergeraert19] in a much broader context. Their properties were studied, among others, by Takens in the nonflat
![]() $C^{\infty }$
case [Reference Takens21] and later by Yoccoz in finite regularity [Reference Yoccoz23]. We next illustrate how to use them with the example above.
$C^{\infty }$
case [Reference Takens21] and later by Yoccoz in finite regularity [Reference Yoccoz23]. We next illustrate how to use them with the example above.
Proof Proof that
 $f,\,g$
are not
$f,\,g$
are not
 $C^2$
conjugate using vector fields.
$C^2$
conjugate using vector fields.
One proof for this particular case that is close to the preceding one works as follows: Let
![]() $X,Y$
be, respectively, the (unique)
$X,Y$
be, respectively, the (unique)
![]() $C^1$
vector fields associated to
$C^1$
vector fields associated to
![]() $f,g$
(according to Takens and Yoccoz, these must be of class
$f,g$
(according to Takens and Yoccoz, these must be of class
![]() $C^{\infty }$
; actually, the expression for Y is explicit, as shown below). For x close to 0, one has (see §3.1 for X):
$C^{\infty }$
; actually, the expression for Y is explicit, as shown below). For x close to 0, one has (see §3.1 for X):
Extend
![]() $X,\,Y$
to
$X,\,Y$
to
![]() $\mathbb {R}_+ := [0, \infty )$
so that their corresponding flows
$\mathbb {R}_+ := [0, \infty )$
so that their corresponding flows
![]() $(f^t)$
and
$(f^t)$
and
![]() $(g^t)$
are made of
$(g^t)$
are made of
![]() $C^{\infty }$
diffeomorphisms of
$C^{\infty }$
diffeomorphisms of
![]() $\mathbb {R}_+$
and are globally contracting. Fix
$\mathbb {R}_+$
and are globally contracting. Fix
![]() $x_0> 0$
. The map
$x_0> 0$
. The map
![]() $\tau _X \!: x\mapsto \int _{x_0}^x\frac 1X$
defines a
$\tau _X \!: x\mapsto \int _{x_0}^x\frac 1X$
defines a
![]() $C^{\infty }$
diffeomorphism from
$C^{\infty }$
diffeomorphism from
![]() $\mathbb {R}_+^* := \, (0,\infty )$
to
$\mathbb {R}_+^* := \, (0,\infty )$
to
![]() $\mathbb {R}$
satisfying
$\mathbb {R}$
satisfying
![]() $\tau _X(f^t(x_0))=t$
by definition of the flow so that
$\tau _X(f^t(x_0))=t$
by definition of the flow so that
![]() $\tau _X^{-1}$
is the map
$\tau _X^{-1}$
is the map
![]() $t\mapsto f^t(x_0)$
. Obviously, one has a similar construction for Y and
$t\mapsto f^t(x_0)$
. Obviously, one has a similar construction for Y and
![]() $(g^t)$
. (We refer to [Reference Eynard-Bontemps and Navas8] for further details of this construction.) In particular, using the equalities
$(g^t)$
. (We refer to [Reference Eynard-Bontemps and Navas8] for further details of this construction.) In particular, using the equalities
 $$ \begin{align*}\int_{x_0}^{f^n (x_0)} \frac{dy}{X(y)} \,\, = \tau_X (f^n(x_0)) \,\, = \,\, n \,\, = \,\, \tau_Y (g^n(x_0)) \,\, = \,\, \int_{x_0}^{g^n (x_0)} \frac{dy}{Y(y)},\end{align*} $$
$$ \begin{align*}\int_{x_0}^{f^n (x_0)} \frac{dy}{X(y)} \,\, = \tau_X (f^n(x_0)) \,\, = \,\, n \,\, = \,\, \tau_Y (g^n(x_0)) \,\, = \,\, \int_{x_0}^{g^n (x_0)} \frac{dy}{Y(y)},\end{align*} $$
one gets equations for the values of
![]() $f^n(x_0), g^n(x_0)$
that easily yield the estimates (10) and (11). Then the very same arguments as in the preceding proof allow to conclude.
$f^n(x_0), g^n(x_0)$
that easily yield the estimates (10) and (11). Then the very same arguments as in the preceding proof allow to conclude.
Another (more direct) argument of proof works as follows. If h is a
![]() $C^2$
diffeomorphism that conjugates f and g, then it must conjugate the associated flows (this is a consequence of the famous Kopell lemma; see, for instance, [Reference Eynard-Bontemps and Navas8, Proposition 2.2]). This means that
$C^2$
diffeomorphism that conjugates f and g, then it must conjugate the associated flows (this is a consequence of the famous Kopell lemma; see, for instance, [Reference Eynard-Bontemps and Navas8, Proposition 2.2]). This means that
![]() $X \cdot Dh = Y \circ h.$
Writing
$X \cdot Dh = Y \circ h.$
Writing
![]() $h (x) = \lambda x + a x^2 + o(x^2)$
, with
$h (x) = \lambda x + a x^2 + o(x^2)$
, with
![]() $\lambda \neq 0$
, this gives
$\lambda \neq 0$
, this gives
By identifying the coefficients of
![]() $x^2$
above, we obtain
$x^2$
above, we obtain
![]() $- \lambda = - \lambda ^2$
, hence
$- \lambda = - \lambda ^2$
, hence
![]() $\lambda = 1$
. Next, by identifying the coefficients of
$\lambda = 1$
. Next, by identifying the coefficients of
![]() $x^3$
, we obtain
$x^3$
, we obtain
which is absurd.
Proof Proof that
 $f,\,g$
are
$f,\,g$
are
 $C^1$
conjugate using vector fields.
$C^1$
conjugate using vector fields.
This is a direct consequence of the much more general result below. For the statement, we say that a (germ of) vector field Z at the origin is contracting (resp. expanding) if its flow maps are contracting (resp. expanding) germs of diffeomorphisms for positive times. Equivalently,
![]() $Z(x) < 0$
(resp.
$Z(x) < 0$
(resp.
![]() $Z(x)> 0$
) for all small-enough
$Z(x)> 0$
) for all small-enough
![]() $x> 0$
.
$x> 0$
.
In all what follows, whenever
![]() $u,v$
are functions of a variable x which are nonzero for
$u,v$
are functions of a variable x which are nonzero for
![]() $x> 0$
, we will write
$x> 0$
, we will write
![]() $u \sim v$
if they satisfy
$u \sim v$
if they satisfy
![]() $\lim _{x \to 0} \frac { u(x) }{ v(x) } = 1$
.
$\lim _{x \to 0} \frac { u(x) }{ v(x) } = 1$
.
Proposition 2.1. Let X and Y be two (germs of) continuous vector fields, both contracting or both expanding, that generate flows of (germs of)
![]() $C^1$
diffeomorphisms. Suppose that there exist
$C^1$
diffeomorphisms. Suppose that there exist
![]() $r>1,s>1$
and
$r>1,s>1$
and
![]() $\alpha \neq 0,\beta \neq 0$
of the same sign satisfying
$\alpha \neq 0,\beta \neq 0$
of the same sign satisfying
![]() $X(x)\sim \alpha x^r$
and
$X(x)\sim \alpha x^r$
and
![]() $Y(x)\sim \beta x^s$
at
$Y(x)\sim \beta x^s$
at
![]() $0$
. Then X and Y are conjugate by the germ of a
$0$
. Then X and Y are conjugate by the germ of a
![]() $C^1$
diffeomorphism if and only if
$C^1$
diffeomorphism if and only if
![]() $r=s$
.
$r=s$
.
Remark 2.2. We will see in the proof that the condition remains necessary if one only assumes
![]() $r \geq 1, s \ge 1$
. However, it is not sufficient anymore if
$r \geq 1, s \ge 1$
. However, it is not sufficient anymore if
![]() $r=s=1$
. In this case, one has to add the condition
$r=s=1$
. In this case, one has to add the condition
![]() $\alpha =\beta $
and, even then, one needs an additional regularity assumption on X and Y (for instance,
$\alpha =\beta $
and, even then, one needs an additional regularity assumption on X and Y (for instance,
![]() $C^{1+\tau }$
with
$C^{1+\tau }$
with
![]() $\tau>0$
is enough [Reference Mann and Wolff11], but
$\tau>0$
is enough [Reference Mann and Wolff11], but
![]() $C^{1+bv}$
and even
$C^{1+bv}$
and even
![]() $C^{1+ac}$
are not [Reference Eynard-Bontemps and Navas8]).
$C^{1+ac}$
are not [Reference Eynard-Bontemps and Navas8]).
Remark 2.3. Proposition 2.1 gives a very simple criterion of
![]() $C^1$
conjugacy for contracting smooth vector fields X and Y which are neither hyperbolic nor infinitely flat at
$C^1$
conjugacy for contracting smooth vector fields X and Y which are neither hyperbolic nor infinitely flat at
![]() $0$
(or for
$0$
(or for
![]() $C^k$
vector fields which are not k-flat). This criterion is simply to have the same order of flatness at
$C^k$
vector fields which are not k-flat). This criterion is simply to have the same order of flatness at
![]() $0$
and the same ‘sign’ or equivalently to satisfy that
$0$
and the same ‘sign’ or equivalently to satisfy that
![]() $X/Y$
has a positive limit at
$X/Y$
has a positive limit at
![]() $0$
(though the statement above is much more general since it does not even require the vector fields to be
$0$
(though the statement above is much more general since it does not even require the vector fields to be
![]() $C^1$
!).
$C^1$
!).
We do not know whether this condition remains sufficient if one considers infinitely flat vector fields. Nevertheless, in this context it is not necessary. For example,
![]() $X(x):=e^{-\frac 1{x}}$
and
$X(x):=e^{-\frac 1{x}}$
and
![]() $Y(x):=\frac 12 e^{-\frac 1{2x}}$
are conjugate by a homothety of ratio
$Y(x):=\frac 12 e^{-\frac 1{2x}}$
are conjugate by a homothety of ratio
![]() $2$
, but
$2$
, but
![]() $Y(x) = \frac 12\sqrt {X(x)}$
, so
$Y(x) = \frac 12\sqrt {X(x)}$
, so
![]() $X/Y$
goes to
$X/Y$
goes to
![]() $0$
. It is not necessary even if one restricts to conjugacies by germs of parabolic
$0$
. It is not necessary even if one restricts to conjugacies by germs of parabolic
![]() $C^1$
diffeomorphisms. For example, consider the vector field
$C^1$
diffeomorphisms. For example, consider the vector field
![]() $X(x):= e^{-\frac 1{x^2}}$
and the local (analytical) diffeomorphism
$X(x):= e^{-\frac 1{x^2}}$
and the local (analytical) diffeomorphism
![]() $h(x):=\frac {x}{1+x}$
. Then
$h(x):=\frac {x}{1+x}$
. Then
![]() $Y=h^*X$
satisfies
$Y=h^*X$
satisfies
 $$ \begin{align*}Y(x) = \frac{(X\circ h)(x)}{Dh(x)}\sim e^{-\frac{(1+x)^2}{x^2}} = X(x) \, e^{-\frac2x-1},\end{align*} $$
$$ \begin{align*}Y(x) = \frac{(X\circ h)(x)}{Dh(x)}\sim e^{-\frac{(1+x)^2}{x^2}} = X(x) \, e^{-\frac2x-1},\end{align*} $$
so
![]() $X/Y$
goes to
$X/Y$
goes to
![]() $+\infty $
.
$+\infty $
.
Proof Proof of the ‘necessity’ in Proposition 2.1.
If h is a germ of
![]() $C^1$
diffeomorphisms conjugating X to Y, then, for
$C^1$
diffeomorphisms conjugating X to Y, then, for
![]() $x>0$
close to the origin,
$x>0$
close to the origin,
 $$ \begin{align*}Dh(x) = \frac{(Y\circ h)(x)}{X(x)}\sim \frac{\beta \, (h(x))^s}{\alpha x^r}\sim \frac{\beta \, (Dh(0))^s}{\alpha} x^{s-r}.\end{align*} $$
$$ \begin{align*}Dh(x) = \frac{(Y\circ h)(x)}{X(x)}\sim \frac{\beta \, (h(x))^s}{\alpha x^r}\sim \frac{\beta \, (Dh(0))^s}{\alpha} x^{s-r}.\end{align*} $$
The last expression must have a nonzero limit at
![]() $0$
, which forces
$0$
, which forces
![]() $r = s$
. Observe that this part of the argument works for any values of r and s. Moreover, if
$r = s$
. Observe that this part of the argument works for any values of r and s. Moreover, if
![]() $r=s=1$
, then, since
$r=s=1$
, then, since
![]() $Dh(x)$
must tend to
$Dh(x)$
must tend to
![]() $Dh(0)\neq 0$
, we have in addition
$Dh(0)\neq 0$
, we have in addition
![]() $\alpha = \beta $
.
$\alpha = \beta $
.
Proof Proof of the ‘sufficiency’ in Proposition 2.1.
Again, extend
![]() $X,Y$
to
$X,Y$
to
![]() $\mathbb {R}_+ = [0, \infty )$
so that they do not vanish outside the origin and their corresponding flows
$\mathbb {R}_+ = [0, \infty )$
so that they do not vanish outside the origin and their corresponding flows
![]() $(f^t)$
and
$(f^t)$
and
![]() $(g^t)$
are made of
$(g^t)$
are made of
![]() $C^1$
diffeomorphisms of
$C^1$
diffeomorphisms of
![]() $\mathbb {R}_+$
. Multiply them by
$\mathbb {R}_+$
. Multiply them by
![]() $-1$
in case they are expanding, fix
$-1$
in case they are expanding, fix
![]() $x_0> 0$
and consider the maps
$x_0> 0$
and consider the maps
![]() $\tau _X \!: x \mapsto \int _{x_0}^x\frac 1X$
and
$\tau _X \!: x \mapsto \int _{x_0}^x\frac 1X$
and
![]() $\tau _Y \!: x \mapsto \int _{x_0}^x \frac {1}{Y}$
. The
$\tau _Y \!: x \mapsto \int _{x_0}^x \frac {1}{Y}$
. The
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $h := \tau _Y^{-1}\circ \tau _X$
of
$h := \tau _Y^{-1}\circ \tau _X$
of
![]() $\mathbb {R}_+^* \!= \, (0,\infty )$
conjugates
$\mathbb {R}_+^* \!= \, (0,\infty )$
conjugates
![]() $(f^t)$
to
$(f^t)$
to
![]() $(g^t)$
and thus sends X to Y. Let us check that, under the assumption
$(g^t)$
and thus sends X to Y. Let us check that, under the assumption
![]() $r=s>1$
, the map h extends to a
$r=s>1$
, the map h extends to a
![]() $C^1$
diffeomorphism of
$C^1$
diffeomorphism of
![]() $\mathbb {R}_+$
. For
$\mathbb {R}_+$
. For
![]() $x>0$
near
$x>0$
near
![]() $0$
, one has
$0$
, one has
 $$ \begin{align*}Dh(x) = \frac{(Y\circ h)(x)}{X(x)}\sim \frac{\beta}{\alpha}\left(\frac{h(x)}{x}\right)^{\! r},\end{align*} $$
$$ \begin{align*}Dh(x) = \frac{(Y\circ h)(x)}{X(x)}\sim \frac{\beta}{\alpha}\left(\frac{h(x)}{x}\right)^{\! r},\end{align*} $$
so it suffices to show that
![]() $\frac {h(x)}{x}$
has a limit at
$\frac {h(x)}{x}$
has a limit at
![]() $0$
. To do this, first observe that the improper integral
$0$
. To do this, first observe that the improper integral
![]() $\int _{x_0}^x\frac {dy}{y^r}$
diverges when x goes to
$\int _{x_0}^x\frac {dy}{y^r}$
diverges when x goes to
![]() $0$
, so
$0$
, so
 $$ \begin{align*}\tau_X(x) = \int_{x_0}^x\frac1X\sim \int_{x_0}^x \frac{dy}{\alpha y^r}\sim -\alpha' x^{1-r}\end{align*} $$
$$ \begin{align*}\tau_X(x) = \int_{x_0}^x\frac1X\sim \int_{x_0}^x \frac{dy}{\alpha y^r}\sim -\alpha' x^{1-r}\end{align*} $$
for some constant
![]() $\alpha '>0$
. Similarly,
$\alpha '>0$
. Similarly,
![]() $\tau _Y(x)\sim -\beta ' x^{1-r}$
. It follows that when t goes to
$\tau _Y(x)\sim -\beta ' x^{1-r}$
. It follows that when t goes to
![]() $\infty $
, one has
$\infty $
, one has
![]() $t = \tau _Y(\tau _Y^{-1}(t))\sim -\beta ' (\tau _Y^{-1}(t))^{1-r}$
so that
$t = \tau _Y(\tau _Y^{-1}(t))\sim -\beta ' (\tau _Y^{-1}(t))^{1-r}$
so that
Finally,
for some new constant
![]() $\beta "'$
, which concludes the proof.
$\beta "'$
, which concludes the proof.
Remark 2.4. The inoffensive relation (14) above is a key step. It does not work for
![]() $r=s=1$
. In this case,
$r=s=1$
. In this case,
![]() $x^{1-r}$
must be replaced by
$x^{1-r}$
must be replaced by
![]() $\varphi (x) := \log (x)$
, but the function
$\varphi (x) := \log (x)$
, but the function
![]() $\varphi $
does not satisfy
$\varphi $
does not satisfy
whereas the power functions do (as it was indeed used in the line just following Equation (14))!
So far we have discussed the
![]() $C^1$
conjugacy between elements in
$C^1$
conjugacy between elements in
![]() $\mathrm {Diff}^1_+ (\mathbb {R},0)$
that are exactly
$\mathrm {Diff}^1_+ (\mathbb {R},0)$
that are exactly
![]() $\ell $
-tangent to the identity for the same value of
$\ell $
-tangent to the identity for the same value of
![]() $\ell $
via two different methods: One of them is direct, and the other one is based on associated vector fields. It turns out, however, that these approaches are somehow equivalent. Indeed, according to Sergeraert [Reference Sergeraert19], the vector field associated to a contracting germ f of class
$\ell $
via two different methods: One of them is direct, and the other one is based on associated vector fields. It turns out, however, that these approaches are somehow equivalent. Indeed, according to Sergeraert [Reference Sergeraert19], the vector field associated to a contracting germ f of class
![]() $C^2$
has an explicit iterative formula:
$C^2$
has an explicit iterative formula:
 $$ \begin{align*}X (x) = \lim_{n \to \infty} (f^n)^* (f-id) ( x ) = \lim_{n \to \infty} \frac{f^{n+1}(x)- f^n (x)}{Df^n (x)}\end{align*} $$
$$ \begin{align*}X (x) = \lim_{n \to \infty} (f^n)^* (f-id) ( x ) = \lim_{n \to \infty} \frac{f^{n+1}(x)- f^n (x)}{Df^n (x)}\end{align*} $$
(we refer to [Reference Eynard-Bontemps and Navas7] for the details and extensions of this construction). Now, if h is a
![]() $C^1$
diffeomorphism that conjugates f to another contracting germ g of
$C^1$
diffeomorphism that conjugates f to another contracting germ g of
![]() $C^2$
diffeomorphism, then, as already mentioned, it must send X to the vector field Y associated to g, that is,
$C^2$
diffeomorphism, then, as already mentioned, it must send X to the vector field Y associated to g, that is,
![]() $X \cdot Dh = Y \circ h$
. Using the iterative formula above, we obtain
$X \cdot Dh = Y \circ h$
. Using the iterative formula above, we obtain
 $$ \begin{align*}Dh (x) = \lim_{n \to \infty} \frac{Df^n (x)}{f^{n+1}(x)-f^n(x)} \cdot \frac{g^{n+1}(h(x)) - g^n (h(x))}{Dg^n (h(x))}.\end{align*} $$
$$ \begin{align*}Dh (x) = \lim_{n \to \infty} \frac{Df^n (x)}{f^{n+1}(x)-f^n(x)} \cdot \frac{g^{n+1}(h(x)) - g^n (h(x))}{Dg^n (h(x))}.\end{align*} $$
Since
![]() $hfh^{-1} = g$
, we have
$hfh^{-1} = g$
, we have
 $$ \begin{align*}\frac{g^{n+1}(h(x)) - g^n (h(x))}{f^{n+1}(x) - f^n (x)} = \frac{ h (f^{n+1}(x))- h (f^n (x))}{f^{n+1}(x)-f^n(x)} \longrightarrow Dh (0).\end{align*} $$
$$ \begin{align*}\frac{g^{n+1}(h(x)) - g^n (h(x))}{f^{n+1}(x) - f^n (x)} = \frac{ h (f^{n+1}(x))- h (f^n (x))}{f^{n+1}(x)-f^n(x)} \longrightarrow Dh (0).\end{align*} $$
As a consequence, if
![]() $Dh (0) = 1$
, we have
$Dh (0) = 1$
, we have
 $$ \begin{align*}Dh (x) = \lim_{n \to \infty} \frac{Df^n(x)}{Dg^n (h(x))},\end{align*} $$
$$ \begin{align*}Dh (x) = \lim_{n \to \infty} \frac{Df^n(x)}{Dg^n (h(x))},\end{align*} $$
and we thus retrieve the equality
![]() $Dh(x) = A (x,h(x))$
from (13).
$Dh(x) = A (x,h(x))$
from (13).
2.2 Examples of low regular conjugacies that preserve residues
The statement of Theorem A would be empty if all
![]() $C^{\ell + 1}$
conjugacies between parabolic germs in
$C^{\ell + 1}$
conjugacies between parabolic germs in
![]() $\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
were automatically
$\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
were automatically
![]() $C^{2\ell + 1}$
. However, this is not at all the case. Below we provide the details of a specific example for which
$C^{2\ell + 1}$
. However, this is not at all the case. Below we provide the details of a specific example for which
![]() $\ell = 1$
; we leave the extension to higher order of tangency to the reader.
$\ell = 1$
; we leave the extension to higher order of tangency to the reader.
Actually, our example directly deals with (flat) vector fields: We will exhibit two of them of class
![]() $C^3$
that are
$C^3$
that are
![]() $C^2$
conjugate but not
$C^2$
conjugate but not
![]() $C^3$
conjugate. The announced diffeomorphisms will be the time-1 maps of their flows.
$C^3$
conjugate. The announced diffeomorphisms will be the time-1 maps of their flows.
Let
![]() $X(x) := x^2$
,
$X(x) := x^2$
,
![]() $h(x) := x+x^2+x^3\log x$
and
$h(x) := x+x^2+x^3\log x$
and
![]() $Y := h^*X$
. One easily checks that h is the germ of
$Y := h^*X$
. One easily checks that h is the germ of
![]() $C^2$
diffeomorphism that is not
$C^2$
diffeomorphism that is not
![]() $C^3$
on any neighborhood of the origin. (This follows from the fact that the function
$C^3$
on any neighborhood of the origin. (This follows from the fact that the function
![]() $x\mapsto x^{k+1} \log x$
is of class
$x\mapsto x^{k+1} \log x$
is of class
![]() $C^k$
but not
$C^k$
but not
![]() $C^{k+1}$
, which can be easily checked by induction.) Every map that conjugates X to Y equals h up to a member of the flow of X (this immediately follows from [Reference Eynard-Bontemps and Navas8, Lemma 2.6]). As these members are all of class
$C^{k+1}$
, which can be easily checked by induction.) Every map that conjugates X to Y equals h up to a member of the flow of X (this immediately follows from [Reference Eynard-Bontemps and Navas8, Lemma 2.6]). As these members are all of class
![]() $C^{\infty }$
and h is not
$C^{\infty }$
and h is not
![]() $C^3$
, there is no
$C^3$
, there is no
![]() $C^3$
conjugacy from X to Y.
$C^3$
conjugacy from X to Y.
We are hence left to show that Y is of class
![]() $C^3$
. To do this, we compute:
$C^3$
. To do this, we compute:
 $$ \begin{align*} Y(x) =\ & \frac{(X\circ h)(x)}{Dh(x)} \\ =\ & \frac{(x+x^2+x^3\log x)^2}{1+2x+3x^2\log x+ x^2} \\ =\ & x^2 \cdot \frac{1+x^2+x^4(\log x)^2+2x+2x^2\log x+2x^3\log x}{1+2x+3x^2\log x+ x^2}\\ =\ & x^2\left(1+\frac{-x^2\log x+2x^3\log x+x^4(\log x)^2}{1+2x+3x^2\log x+ x^2}\right)\\ =\ & x^2+x^4\log x \cdot \frac{-1+2x+x^2\log x}{1+2x+3x^2\log x+ x^2}. \end{align*} $$
$$ \begin{align*} Y(x) =\ & \frac{(X\circ h)(x)}{Dh(x)} \\ =\ & \frac{(x+x^2+x^3\log x)^2}{1+2x+3x^2\log x+ x^2} \\ =\ & x^2 \cdot \frac{1+x^2+x^4(\log x)^2+2x+2x^2\log x+2x^3\log x}{1+2x+3x^2\log x+ x^2}\\ =\ & x^2\left(1+\frac{-x^2\log x+2x^3\log x+x^4(\log x)^2}{1+2x+3x^2\log x+ x^2}\right)\\ =\ & x^2+x^4\log x \cdot \frac{-1+2x+x^2\log x}{1+2x+3x^2\log x+ x^2}. \end{align*} $$
This shows that Y is of the form
![]() $Y(x) = x^2 + o( x^4 \log x)$
. Showing that Y is of class
$Y(x) = x^2 + o( x^4 \log x)$
. Showing that Y is of class
![]() $C^3$
(with derivatives equal to those of
$C^3$
(with derivatives equal to those of
![]() $x^2$
up to order 3 at the origin) requires some extra computational work based on the fact that the function
$x^2$
up to order 3 at the origin) requires some extra computational work based on the fact that the function
![]() $u (x) := x^4\log x$
satisfies
$u (x) := x^4\log x$
satisfies
![]() $D^{(3-n)} u (x) = o(x^{n})$
for
$D^{(3-n)} u (x) = o(x^{n})$
for
![]() $n \in [\![0,3]\!] := \{0,1,2,3\}$
. We leave the details to the reader.
$n \in [\![0,3]\!] := \{0,1,2,3\}$
. We leave the details to the reader.
2.3
 $C^{2\ell +1}$
germs with vanishing residue that are non
$C^{2\ell +1}$
germs with vanishing residue that are non
 $C^{\ell +1}$
conjugate
$C^{\ell +1}$
conjugate
The aim of this section is to give an example showing that the converse to Theorem A does not hold (for
![]() $\ell = 1$
). More precisely, we will give an example of two expanding germs of
$\ell = 1$
). More precisely, we will give an example of two expanding germs of
![]() $C^3$
diffeomorphisms, both exactly 1-tangent to the identity and with vanishing iterative residue, that are not
$C^3$
diffeomorphisms, both exactly 1-tangent to the identity and with vanishing iterative residue, that are not
![]() $C^2$
conjugate. Notice that, by Proposition 2.1, these are
$C^2$
conjugate. Notice that, by Proposition 2.1, these are
![]() $C^1$
conjugate.
$C^1$
conjugate.
Again, our example directly deals with (flat) vector fields. Namely, let
![]() $X(x):= x^2$
and
$X(x):= x^2$
and
![]() $Y(x) := h^* X (x)$
, where h is given on
$Y(x) := h^* X (x)$
, where h is given on
![]() $\mathbb {R}_+^* $
by
$\mathbb {R}_+^* $
by
![]() $h(x) := x + x^2 \, \log (\log x).$
Let f (resp. g) denote the time-1 map of X (resp. Y). We claim that these are (germs of)
$h(x) := x + x^2 \, \log (\log x).$
Let f (resp. g) denote the time-1 map of X (resp. Y). We claim that these are (germs of)
![]() $C^3$
diffeomorphisms. This is obvious for f (which is actually real-analytic). For g, this follows from the fact that Y is of class
$C^3$
diffeomorphisms. This is obvious for f (which is actually real-analytic). For g, this follows from the fact that Y is of class
![]() $C^3$
. To check this, observe that
$C^3$
. To check this, observe that
 $$ \begin{align*}Y(x) = \frac{X(h(x))}{Dh (x)} = \frac{ \big( x+x^2 \log (\log x) \big)^2}{ 1 + 2 x \log(\log x) + \frac{x}{\log x} },\end{align*} $$
$$ \begin{align*}Y(x) = \frac{X(h(x))}{Dh (x)} = \frac{ \big( x+x^2 \log (\log x) \big)^2}{ 1 + 2 x \log(\log x) + \frac{x}{\log x} },\end{align*} $$
hence, skipping a few steps,
 $$ \begin{align} Y(x) = x^2 + x^3 \cdot \frac{ x \, (\log (\log x))^2 - \frac{1}{\log x}}{1 + 2 x \log(\log(x)) + \frac{x}{\log(x)} } = x^2 + o(x^3). \end{align} $$
$$ \begin{align} Y(x) = x^2 + x^3 \cdot \frac{ x \, (\log (\log x))^2 - \frac{1}{\log x}}{1 + 2 x \log(\log(x)) + \frac{x}{\log(x)} } = x^2 + o(x^3). \end{align} $$
Now, letting
 $$ \begin{align*}u(x) := x^3, \qquad v(x):= \frac{ x \, (\log (\log x))^2 - \frac{1}{\log x}}{1 + 2 x \log(\log x) + \frac{x}{\log x} },\end{align*} $$
$$ \begin{align*}u(x) := x^3, \qquad v(x):= \frac{ x \, (\log (\log x))^2 - \frac{1}{\log x}}{1 + 2 x \log(\log x) + \frac{x}{\log x} },\end{align*} $$
we have
![]() $Y(x) = x^2 + (u v) (x)$
, and
$Y(x) = x^2 + (u v) (x)$
, and
 $$ \begin{align*}D^{(3)} (uv) (x) = \sum_{j=0}^3 {3 \choose j} \, D^{(3-j)} u (x) \, D^{(j)} (v)(x) = \sum_{j=0}^3 c_j \, x^j \, D^{(j)} v(x)\end{align*} $$
$$ \begin{align*}D^{(3)} (uv) (x) = \sum_{j=0}^3 {3 \choose j} \, D^{(3-j)} u (x) \, D^{(j)} (v)(x) = \sum_{j=0}^3 c_j \, x^j \, D^{(j)} v(x)\end{align*} $$
for certain constants
![]() $c_j$
. We are hence reduced to showing that
$c_j$
. We are hence reduced to showing that
![]() $x^j D^{(j)}v(x)$
tends to
$x^j D^{(j)}v(x)$
tends to
![]() $0$
as x goes to the origin, which is straightforward and is left to the reader.
$0$
as x goes to the origin, which is straightforward and is left to the reader.
It will follow from §3.1 (see Equation (17)) that both f and g have vanishing iterative residue. They are conjugated by h, which is the germ of a
![]() $C^1$
diffeomorphism which is easily seen to be non
$C^1$
diffeomorphism which is easily seen to be non
![]() $C^2$
. As in the previous example, this implies that there is no
$C^2$
. As in the previous example, this implies that there is no
![]() $C^2$
conjugacy between f and g (despite they are both
$C^2$
conjugacy between f and g (despite they are both
![]() $C^3$
and have vanishing iterative residue !).
$C^3$
and have vanishing iterative residue !).
3 On the conjugacy invariance of residues
In this section, we give two proofs of Theorem A that generalize those given in the particular case previously treated. In most of the arguments of both proofs, a careful study of the associated vector fields is crucial. In particular, a key argument rests on a very subtle property, namely, the fact that for nonflat germs of
![]() $C^k$
diffeomorphisms, these vector fields are still k times differentiable at the origin, despite they may fail to be of class
$C^k$
diffeomorphisms, these vector fields are still k times differentiable at the origin, despite they may fail to be of class
![]() $C^k$
(as mentioned before, they are ensured to be
$C^k$
(as mentioned before, they are ensured to be
![]() $C^{k-1}$
). Quite surprisingly, this is not explicitly stated this way in Yoccoz’ paper [Reference Yoccoz23, Appendice 3], though it follows directly from §8 therein. More precisely, it corresponds to his second condition
$C^{k-1}$
). Quite surprisingly, this is not explicitly stated this way in Yoccoz’ paper [Reference Yoccoz23, Appendice 3], though it follows directly from §8 therein. More precisely, it corresponds to his second condition
![]() $(C_i)$
for
$(C_i)$
for
![]() $i=k-1$
. (Compare [Reference Eynard-Bontemps and Navas8, Lemma 1.1], which is the analogous property in the hyperbolic case.)
$i=k-1$
. (Compare [Reference Eynard-Bontemps and Navas8, Lemma 1.1], which is the analogous property in the hyperbolic case.)
It is worth pointing out that, however, one of our proofs avoids the use of vector fields. Although this makes it longer, it remains completely elementary. It is closely related to classical arguments of Fatou regarding linearizations of parabolic germs of complex analytic maps [Reference Carlesson and Gamelin4]; compare [Reference Resman18].
3.1 Residues and vector fields
We begin by recalling Yoccoz’ result and, in particular, by relating the residue to their infinitesimal expression.
Let
![]() $\mathbb {K}$
be a field. For each integer
$\mathbb {K}$
be a field. For each integer
![]() $k \geq 1$
, let us consider the group
$k \geq 1$
, let us consider the group
![]() $G_k (\mathbb {K})$
made of the expressions of the form
$G_k (\mathbb {K})$
made of the expressions of the form
 $$ \begin{align*}\sum_{n=1}^k a_n x^n, \quad \mbox{ with } \, a_1 \neq 0,\end{align*} $$
$$ \begin{align*}\sum_{n=1}^k a_n x^n, \quad \mbox{ with } \, a_1 \neq 0,\end{align*} $$
where the product is just the standard composition but neglecting terms of order larger than k. The group
![]() $\widehat {\mathrm {Diff}} (\mathbb {K},0)$
has a natural morphism into each group
$\widehat {\mathrm {Diff}} (\mathbb {K},0)$
has a natural morphism into each group
![]() $G_k (\mathbb {K})$
obtained by truncating series expansions at order k:
$G_k (\mathbb {K})$
obtained by truncating series expansions at order k:
 $$ \begin{align*}\sum_{n \geq 1} a_n x^n \in \widehat{\mathrm{Diff}} (\mathbb{K},0) \quad \longrightarrow \quad \sum_{n=1}^{k} a_n x^n \in G_k (\mathbb{K}).\end{align*} $$
$$ \begin{align*}\sum_{n \geq 1} a_n x^n \in \widehat{\mathrm{Diff}} (\mathbb{K},0) \quad \longrightarrow \quad \sum_{n=1}^{k} a_n x^n \in G_k (\mathbb{K}).\end{align*} $$
Notice that each group
![]() $G_k (\mathbb {K})$
is solvable and finite-dimensional. Moreover, each subgroup
$G_k (\mathbb {K})$
is solvable and finite-dimensional. Moreover, each subgroup
![]() $G_{k,\ell } (\mathbb {K})$
,
$G_{k,\ell } (\mathbb {K})$
,
![]() $\ell < k$
, obtained by truncation as above of elements in
$\ell < k$
, obtained by truncation as above of elements in
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
is nilpotent. In the case where
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
is nilpotent. In the case where
![]() $\mathbb {K}$
is the field of real numbers, these groups have a well-defined exponential map, and every group element is the time-1 element of a unique flow.
$\mathbb {K}$
is the field of real numbers, these groups have a well-defined exponential map, and every group element is the time-1 element of a unique flow.
Actually, it is not very hard to explicitly compute this flow for elements
![]() $\mathrm {f} \in G_{2\ell + 1,\ell } (\mathbb {K})$
, that is for those of the form
$\mathrm {f} \in G_{2\ell + 1,\ell } (\mathbb {K})$
, that is for those of the form
 $$ \begin{align*}\mathrm{f} \, (x) = x + \sum_{n=\ell + 1}^{2\ell + 1} a_n x^n.\end{align*} $$
$$ \begin{align*}\mathrm{f} \, (x) = x + \sum_{n=\ell + 1}^{2\ell + 1} a_n x^n.\end{align*} $$
Namely, this is given by
 $$ \begin{align} \mathrm{f}^t (x) = x + \sum_{n=\ell + 1}^{2 \ell} t \, a_n \, x^n + \left[ \frac{\ell + 1}{2} (t \, a_{\ell})^2 - t \, \mathrm{Resad}_{\ell} (\mathrm{f}) \right] x^{2\ell + 1}, \end{align} $$
$$ \begin{align} \mathrm{f}^t (x) = x + \sum_{n=\ell + 1}^{2 \ell} t \, a_n \, x^n + \left[ \frac{\ell + 1}{2} (t \, a_{\ell})^2 - t \, \mathrm{Resad}_{\ell} (\mathrm{f}) \right] x^{2\ell + 1}, \end{align} $$
where
![]() $\mathrm {Resad}_{\ell }$
is defined as in
$\mathrm {Resad}_{\ell }$
is defined as in
![]() $\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
by Equation (2) (assuming that
$\widehat {\mathrm {Diff}_{\ell }}(\mathbb {K},0)$
by Equation (2) (assuming that
![]() $\mathbb {K}$
has characteristic different from
$\mathbb {K}$
has characteristic different from
![]() $2$
). Checking that this is indeed a flow is straightforward: It only uses the additive properties of the corresponding versions of
$2$
). Checking that this is indeed a flow is straightforward: It only uses the additive properties of the corresponding versions of
![]() $\Phi _{\ell ,i}$
(for
$\Phi _{\ell ,i}$
(for
![]() $1\leq i \leq \ell $
) and
$1\leq i \leq \ell $
) and
![]() $\mathrm {Resad}_{\ell }$
in
$\mathrm {Resad}_{\ell }$
in
![]() $G_{2\ell + 1}(\mathbb {K})$
.
$G_{2\ell + 1}(\mathbb {K})$
.
Inspired by the work of Takens [Reference Takens21], in [Reference Yoccoz23, Appendice 3], Yoccoz considered germs f of nonflat
![]() $C^k$
diffeomorphisms of the real line fixing the origin. In particular, he proved that there exists a unique (germ of)
$C^k$
diffeomorphisms of the real line fixing the origin. In particular, he proved that there exists a unique (germ of)
![]() $C^{k-1}$
vector field X that is k times differentiable at the origin and whose flow
$C^{k-1}$
vector field X that is k times differentiable at the origin and whose flow
![]() $(f^t)$
has time-1 map
$(f^t)$
has time-1 map
![]() $f^1 = f$
.
$f^1 = f$
.
If
![]() $k = 2\ell + 1$
, by truncating f at order
$k = 2\ell + 1$
, by truncating f at order
![]() $2\ell + 1$
, we get an element
$2\ell + 1$
, we get an element
![]() $\mathrm {f}_{2\ell + 1} \in G_{2\ell + 1} (\mathbb {R})$
, and we can hence consider the flow
$\mathrm {f}_{2\ell + 1} \in G_{2\ell + 1} (\mathbb {R})$
, and we can hence consider the flow
![]() $( \mathrm {f}^t_{2\ell + 1})$
in
$( \mathrm {f}^t_{2\ell + 1})$
in
![]() $G_{2\ell + 1} (\mathbb {R})$
whose time-1 element is
$G_{2\ell + 1} (\mathbb {R})$
whose time-1 element is
![]() $\mathrm {f}_{2\ell + 1}$
. Let P be the associated polynomial vector field defined by
$\mathrm {f}_{2\ell + 1}$
. Let P be the associated polynomial vector field defined by
As a key step of his proof, Yoccoz showed a general estimate that implies that
According to Equation (16), if
![]() $f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0)$
writes in the form
$f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0)$
writes in the form
 $$ \begin{align*}f(x) = x + \sum_{n=\ell + 1}^{2\ell + 1} a_n x^n + o (x^{2\ell + 1}),\end{align*} $$
$$ \begin{align*}f(x) = x + \sum_{n=\ell + 1}^{2\ell + 1} a_n x^n + o (x^{2\ell + 1}),\end{align*} $$
then the polynomial vector field associated to
![]() $\mathrm {f}_{2\ell + 1}$
equals
$\mathrm {f}_{2\ell + 1}$
equals
 $$ \begin{align*}P(x) = \frac{d}{dt}_{ |_{t=0}} \mathrm{f}^t_{2\ell + 1} (x) = \sum_{n=\ell + 1}^{2 \ell} a_n x^n - \mathrm{Resad}_{\ell}(f) \, x^{2\ell + 1},\end{align*} $$
$$ \begin{align*}P(x) = \frac{d}{dt}_{ |_{t=0}} \mathrm{f}^t_{2\ell + 1} (x) = \sum_{n=\ell + 1}^{2 \ell} a_n x^n - \mathrm{Resad}_{\ell}(f) \, x^{2\ell + 1},\end{align*} $$
and therefore
 $$ \begin{align} X (x) = \sum_{n=\ell + 1}^{2\ell} a_n x^n - \mathrm{Resad}_{\ell}(f) \, x^{2\ell + 1} + o(x^{2\ell + 1}). \end{align} $$
$$ \begin{align} X (x) = \sum_{n=\ell + 1}^{2\ell} a_n x^n - \mathrm{Resad}_{\ell}(f) \, x^{2\ell + 1} + o(x^{2\ell + 1}). \end{align} $$
This formula in which
![]() $\mathrm {Resad}_{\ell }$
explicitly appears will be fundamental for the proof of Theorem A.
$\mathrm {Resad}_{\ell }$
explicitly appears will be fundamental for the proof of Theorem A.
Remark 3.1. Formula (7), which holds for every
![]() $f \in \mathrm {Diff}^{2\ell + 2}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 2}_{\ell +1} (\mathbb {R},0)$
and all
$f \in \mathrm {Diff}^{2\ell + 2}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 2}_{\ell +1} (\mathbb {R},0)$
and all
![]() $t \neq 0$
, follows from Equation (17) above. Indeed, in order to check it, we may assume that f is expanding and already in reduced form, say
$t \neq 0$
, follows from Equation (17) above. Indeed, in order to check it, we may assume that f is expanding and already in reduced form, say
If X is the
![]() $C^{2\ell +1}$
vector field associated to f, then the vector field
$C^{2\ell +1}$
vector field associated to f, then the vector field
![]() $X_t$
associated to
$X_t$
associated to
![]() $f^t$
is
$f^t$
is
![]() $t X$
. Since
$t X$
. Since
by Equation (17) we have
where
![]() $\mu _t$
is such that
$\mu _t$
is such that
![]() $\mathrm {Resad}_{\ell } (f^t) = t \, \mathrm {Resad}_{\ell } (f)$
. Hence,
$\mathrm {Resad}_{\ell } (f^t) = t \, \mathrm {Resad}_{\ell } (f)$
. Hence,
 $$ \begin{align*}\frac{(\ell +1) \, t^2}{2} - \mu_t = t \, \left[ \frac{\ell + 1}{2} - \mu \right].\end{align*} $$
$$ \begin{align*}\frac{(\ell +1) \, t^2}{2} - \mu_t = t \, \left[ \frac{\ell + 1}{2} - \mu \right].\end{align*} $$
Therefore, for
![]() $t> 0$
,
$t> 0$
,
 $$ \begin{align*}\mathrm{Resit} (f^t) \kern1.3pt{=}\kern1.3pt \frac{\ell +1}{2} \kern1.3pt{-}\kern1.3pt \frac{\mu_t}{t^2} \kern1.3pt{=}\kern1.3pt \frac{1}{t^2} \left[ \frac{(\ell +1) \kern1.3pt t^2}{2} \kern1.3pt{-}\kern1.3pt \mu_t \right] \kern1.3pt{=}\kern1.3pt \frac{t}{t^2} \kern1.3pt \left[ \frac{\ell + 1}{2} \kern1.3pt{-}\kern1.3pt \mu \right] \kern1.3pt{=}\kern1.3pt \frac{1}{t} \kern1.3pt \left[ \frac{\ell + 1}{2} \kern1.3pt{-}\kern1.3pt \mu \right] \kern1.3pt{=}\kern1.3pt \frac{\mathrm{Resit} (f)}{t},\end{align*} $$
$$ \begin{align*}\mathrm{Resit} (f^t) \kern1.3pt{=}\kern1.3pt \frac{\ell +1}{2} \kern1.3pt{-}\kern1.3pt \frac{\mu_t}{t^2} \kern1.3pt{=}\kern1.3pt \frac{1}{t^2} \left[ \frac{(\ell +1) \kern1.3pt t^2}{2} \kern1.3pt{-}\kern1.3pt \mu_t \right] \kern1.3pt{=}\kern1.3pt \frac{t}{t^2} \kern1.3pt \left[ \frac{\ell + 1}{2} \kern1.3pt{-}\kern1.3pt \mu \right] \kern1.3pt{=}\kern1.3pt \frac{1}{t} \kern1.3pt \left[ \frac{\ell + 1}{2} \kern1.3pt{-}\kern1.3pt \mu \right] \kern1.3pt{=}\kern1.3pt \frac{\mathrm{Resit} (f)}{t},\end{align*} $$
as announced. The case
![]() $t < 0$
is analogous.
$t < 0$
is analogous.
It is worth mentioning that the argument above shows that the equality (7) holds for every
![]() $f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell +1} (\mathbb {R},0)$
and all
$f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell +1} (\mathbb {R},0)$
and all
![]() $t \neq 0$
for which
$t \neq 0$
for which
![]() $f^t$
is a germ of
$f^t$
is a germ of
![]() $C^{2\ell +1}$
diffeomorphism (or, at least, has
$C^{2\ell +1}$
diffeomorphism (or, at least, has
![]() $(2\ell +1)$
derivatives at the origin; see Remark 1.4).
$(2\ell +1)$
derivatives at the origin; see Remark 1.4).
3.2 A first proof of the
 $C^{\ell + 1}$
conjugacy invariance of
$C^{\ell + 1}$
conjugacy invariance of
 $\mathbf {Resit}$
$\mathbf {Resit}$
We next proceed to the proof of the
![]() $C^{\ell + 1}$
conjugacy invariance of
$C^{\ell + 1}$
conjugacy invariance of
![]() $\mathrm {Resit}$
between germs of
$\mathrm {Resit}$
between germs of
![]() $C^{2\ell + 1}$
diffeomorphisms that are exactly
$C^{2\ell + 1}$
diffeomorphisms that are exactly
![]() $\ell $
-tangent to the identity.
$\ell $
-tangent to the identity.
Proof Proof of Theorem A
Let f and g be elements in
![]() $\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
conjugated by an element
$\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
conjugated by an element
![]() $h \in \mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
. Then they are both contracting or both expanding. We will suppose that the second case holds; the other one follows from it by passing to inverses.
$h \in \mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
. Then they are both contracting or both expanding. We will suppose that the second case holds; the other one follows from it by passing to inverses.
As we want to show the equality
![]() $\mathrm {Resit} (f) = \mathrm {Resit} (g)$
, by the definition and Lemma 1.3, we may assume that f and g have Taylor series expansions at the origin of the form
$\mathrm {Resit} (f) = \mathrm {Resit} (g)$
, by the definition and Lemma 1.3, we may assume that f and g have Taylor series expansions at the origin of the form
Notice that
In virtue of Equation (17), the vector fields
![]() $X,Y$
associated to
$X,Y$
associated to
![]() $f,g$
, respectively, have the form
$f,g$
, respectively, have the form
Now, write
 $$ \begin{align*}h(x) = \lambda \, x + \sum_{n =2}^{\ell + 1} c_n x^n + o(x^{\ell + 1}).\end{align*} $$
$$ \begin{align*}h(x) = \lambda \, x + \sum_{n =2}^{\ell + 1} c_n x^n + o(x^{\ell + 1}).\end{align*} $$
Since h conjugates f to g, it must conjugate X to Y, that is,
We first claim that this implies
![]() $\lambda = 1$
. Indeed, the relation writes in a summarized way as
$\lambda = 1$
. Indeed, the relation writes in a summarized way as
By identification of the coefficients of
![]() $x^{\ell + 1}$
, we obtain
$x^{\ell + 1}$
, we obtain
![]() $\lambda = \lambda ^{\ell + 1}$
. Thus,
$\lambda = \lambda ^{\ell + 1}$
. Thus,
![]() $\lambda = 1$
, as announced.
$\lambda = 1$
, as announced.
We next claim that h must be
![]() $\ell $
-tangent to the identity. Indeed, assume otherwise and let
$\ell $
-tangent to the identity. Indeed, assume otherwise and let
![]() $2 \leq p < \ell + 1$
be the smallest index for which
$2 \leq p < \ell + 1$
be the smallest index for which
![]() $c_p \neq 0$
. Then relation (18) above may be summarized as
$c_p \neq 0$
. Then relation (18) above may be summarized as
By identifying the coefficients of
![]() $x^{\ell +p}$
we obtain
$x^{\ell +p}$
we obtain
![]() $p \, c_p = (\ell + 1) \, c_p$
, which is impossible for
$p \, c_p = (\ell + 1) \, c_p$
, which is impossible for
![]() $c_p \neq 0$
.
$c_p \neq 0$
.
Thus, h writes in the form
Relation (18) then becomes
 $$ \begin{align*}&( x^{\ell + 1} - R x^{2\ell + 1} + o (x^{2\ell + 1})) \cdot (1 + (\ell + 1) c x^{\ell} + o(x^{\ell})) \\&\quad= (x + cx^{\ell + 1} + o(x^{\ell + 1}))^{\ell + 1} - R' (x + o(x^{\ell}))^{2\ell + 1} + o(x^{2\ell + 1}).\end{align*} $$
$$ \begin{align*}&( x^{\ell + 1} - R x^{2\ell + 1} + o (x^{2\ell + 1})) \cdot (1 + (\ell + 1) c x^{\ell} + o(x^{\ell})) \\&\quad= (x + cx^{\ell + 1} + o(x^{\ell + 1}))^{\ell + 1} - R' (x + o(x^{\ell}))^{2\ell + 1} + o(x^{2\ell + 1}).\end{align*} $$
Identification of the coefficients of
![]() $x^{2\ell + 1}$
then gives
$x^{2\ell + 1}$
then gives
Therefore,
![]() $R=R'$
, as we wanted to show.
$R=R'$
, as we wanted to show.
3.3 Residues and logarithmic deviations of orbits
We next characterize
![]() $\mathrm {Resit}$
for contracting germs
$\mathrm {Resit}$
for contracting germs
![]() $f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
in terms of the deviation of orbits from those of the corresponding (parabolic) ramified affine flow of order
$f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
in terms of the deviation of orbits from those of the corresponding (parabolic) ramified affine flow of order
![]() $\ell $
, namely,
$\ell $
, namely,
 $$ \begin{align*}f^t(x) := \frac{x}{\sqrt[\ell]{1 + t x^{\ell}}} = x - \frac{t}{\ell} x^{\ell + 1} + \frac{1}{2 \, \ell} \left( 1+\frac{1}{\ell} \right) t^2 x^{2\ell + 1} + o (x^{2\ell + 1}).\end{align*} $$
$$ \begin{align*}f^t(x) := \frac{x}{\sqrt[\ell]{1 + t x^{\ell}}} = x - \frac{t}{\ell} x^{\ell + 1} + \frac{1}{2 \, \ell} \left( 1+\frac{1}{\ell} \right) t^2 x^{2\ell + 1} + o (x^{2\ell + 1}).\end{align*} $$
Notice that the time-1 map
![]() $f := f^1$
of this flow satisfies
$f := f^1$
of this flow satisfies
![]() $\mathrm {Resit} (f) = 0$
. Moreover, for all
$\mathrm {Resit} (f) = 0$
. Moreover, for all
![]() $x>0$
,
$x>0$
,
which asymtotically behaves (when n goes to infinity) as
 $$ \begin{align*}\frac{n^{\frac{\ell-1}{\ell}}}{\ell \, n \, (1+nx^{\ell})} \sim \frac{1}{\ell \, n \, \sqrt[\ell]{n}},\end{align*} $$
$$ \begin{align*}\frac{n^{\frac{\ell-1}{\ell}}}{\ell \, n \, (1+nx^{\ell})} \sim \frac{1}{\ell \, n \, \sqrt[\ell]{n}},\end{align*} $$
where the first equivalence follows from the equality
![]() $u^{\ell } - v^{\ell } = (u-v) (u^{\ell -1} + u^{\ell -2}v + \ldots + v^{\ell -1})$
. In particular, letting
$u^{\ell } - v^{\ell } = (u-v) (u^{\ell -1} + u^{\ell -2}v + \ldots + v^{\ell -1})$
. In particular, letting
![]() $a = 1/\ell $
, we have
$a = 1/\ell $
, we have
 $$ \begin{align*}\lim_{n \to \infty} \left[ \frac{ \ell \, n \, \sqrt[\ell]{a \, \ell \, n} }{\log (n)} \left( \frac{1}{ \sqrt[\ell]{a \, \ell \, n}} - f^n (x)\right) \right] = 0.\end{align*} $$
$$ \begin{align*}\lim_{n \to \infty} \left[ \frac{ \ell \, n \, \sqrt[\ell]{a \, \ell \, n} }{\log (n)} \left( \frac{1}{ \sqrt[\ell]{a \, \ell \, n}} - f^n (x)\right) \right] = 0.\end{align*} $$
This is a particular case of the general proposition below.
Proposition 3.2. If
![]() $\ell \geq 1$
, then, for every contracting germ
$\ell \geq 1$
, then, for every contracting germ
![]() $f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
of the form
$f \in \mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
of the form
and all
![]() $x_0> 0$
, one has
$x_0> 0$
, one has
 $$ \begin{align} \mathrm{Resit} (f) = \lim_{n \to \infty} \left[ \frac{a \, \ell^2 \, n^2}{\log (n)} \left( \frac{1}{a \, \ell \, n} -[ f^n (x_0)]^{\ell}\right) \right] = \lim_{n \to \infty} \left[ \frac{ \ell \, n \, \sqrt[\ell]{a \, \ell \, n} }{\log (n)} \left( \frac{1}{ \sqrt[\ell]{a \, \ell \, n}} - f^n (x_0)\right) \right]. \end{align} $$
$$ \begin{align} \mathrm{Resit} (f) = \lim_{n \to \infty} \left[ \frac{a \, \ell^2 \, n^2}{\log (n)} \left( \frac{1}{a \, \ell \, n} -[ f^n (x_0)]^{\ell}\right) \right] = \lim_{n \to \infty} \left[ \frac{ \ell \, n \, \sqrt[\ell]{a \, \ell \, n} }{\log (n)} \left( \frac{1}{ \sqrt[\ell]{a \, \ell \, n}} - f^n (x_0)\right) \right]. \end{align} $$
Proof First proof (using coordinates at infinity).
Consider the map
![]() $I (z) = 1/z^{1 / \ell }$
, where
$I (z) = 1/z^{1 / \ell }$
, where
![]() $z> 0$
is large enough. Then the conjugate germ at infinity
$z> 0$
is large enough. Then the conjugate germ at infinity
![]() $g := I^{-1} f I$
has an expansion of the form
$g := I^{-1} f I$
has an expansion of the form
 $$ \begin{align*}g(z) = \left( \frac{1}{\frac{1}{z^{1/\ell}} - \frac{a}{z^{(\ell+1)/\ell}} + \frac{b}{z^{(2\ell+1)/\ell}} + ...} \right)^{\ell} = z \left( \frac{1}{1 - \frac{a}{z} + \frac{b}{z^2} + \ldots} \right)^{\ell}.\end{align*} $$
$$ \begin{align*}g(z) = \left( \frac{1}{\frac{1}{z^{1/\ell}} - \frac{a}{z^{(\ell+1)/\ell}} + \frac{b}{z^{(2\ell+1)/\ell}} + ...} \right)^{\ell} = z \left( \frac{1}{1 - \frac{a}{z} + \frac{b}{z^2} + \ldots} \right)^{\ell}.\end{align*} $$
Hence,
 $$ \begin{align*}g(z) = z \left( 1 + \left(\frac{a}{z} - \frac{b}{z^2} - \ldots \right) + \left(\frac{a}{z} - \frac{b}{z^2} - \ldots \right)^2 + \ldots \right)^{\ell} = z \left( 1 + \frac{a}{z} + \frac{a^2 - b}{z^2} + O \left( \frac{1}{z^3} \right) \right)^{\ell},\end{align*} $$
$$ \begin{align*}g(z) = z \left( 1 + \left(\frac{a}{z} - \frac{b}{z^2} - \ldots \right) + \left(\frac{a}{z} - \frac{b}{z^2} - \ldots \right)^2 + \ldots \right)^{\ell} = z \left( 1 + \frac{a}{z} + \frac{a^2 - b}{z^2} + O \left( \frac{1}{z^3} \right) \right)^{\ell},\end{align*} $$
that is
 $$ \begin{align*}g(z) = z \left( 1 + \ell \left( \frac{a}{z} + \frac{a^2 - b}{z^2} \right) + \frac{\ell (\ell-1)}{2} \left( \frac{a}{z} \right)^2 + O \left( \frac{1}{z^3}\right) \right).\end{align*} $$
$$ \begin{align*}g(z) = z \left( 1 + \ell \left( \frac{a}{z} + \frac{a^2 - b}{z^2} \right) + \frac{\ell (\ell-1)}{2} \left( \frac{a}{z} \right)^2 + O \left( \frac{1}{z^3}\right) \right).\end{align*} $$
Therefore,
 $$ \begin{align} g(z) = z + a\ell + \frac{\ell}{z} \left[ \frac{(\ell + 1) a^2}{2} - b \right] + O \left( \frac{1}{z^2}\right) = z + a\ell + \frac{R \ell}{z} + O \left( \frac{1}{z^2}\right), \end{align} $$
$$ \begin{align} g(z) = z + a\ell + \frac{\ell}{z} \left[ \frac{(\ell + 1) a^2}{2} - b \right] + O \left( \frac{1}{z^2}\right) = z + a\ell + \frac{R \ell}{z} + O \left( \frac{1}{z^2}\right), \end{align} $$
where
![]() $R = \mathrm {Resad}_{\ell } (f)$
. We claim that, for each fixed z, the sequence below converges as n goes to infinity:
$R = \mathrm {Resad}_{\ell } (f)$
. We claim that, for each fixed z, the sequence below converges as n goes to infinity:
Assume this for a while. Then we have
hence
 $$ \begin{align*}R = \lim_{n \to \infty} \frac{a}{\ell \log(n)} \big[ I^{-1} f^n (x_0) - a \ell n \big] = \lim_{n \to \infty} \frac{a}{\ell \log(n)} \left[ \frac{1}{f^n (x_0)^{\ell}} - a \ell n \right].\end{align*} $$
$$ \begin{align*}R = \lim_{n \to \infty} \frac{a}{\ell \log(n)} \big[ I^{-1} f^n (x_0) - a \ell n \big] = \lim_{n \to \infty} \frac{a}{\ell \log(n)} \left[ \frac{1}{f^n (x_0)^{\ell}} - a \ell n \right].\end{align*} $$
This easily implies that
Moreover, using the identity
![]() $u^{\ell } - v^{\ell } = (u-v) (u^{\ell -1} + u^{\ell -2}v + \ldots + v^{\ell -1})$
, one easily deduces that
$u^{\ell } - v^{\ell } = (u-v) (u^{\ell -1} + u^{\ell -2}v + \ldots + v^{\ell -1})$
, one easily deduces that
 $$ \begin{align*}R &= \lim_{n \to \infty} \frac{ a \ell (a \ell n)^{(\ell-1)/\ell}}{\ell \log(n)} \left[ \frac{1}{f^n (x_0)} - (a \ell n)^{1/\ell} \right] \\&= \lim_{n \to \infty} \frac{ a (a \ell n)^{(\ell-1)/\ell}}{\log(n)} \left[ \frac{1}{ (a \ell n)^{1/\ell}} - f^{n}(x_0) \right] \frac{(a \ell n)^{1/\ell}}{f^n(x_0)}.\end{align*} $$
$$ \begin{align*}R &= \lim_{n \to \infty} \frac{ a \ell (a \ell n)^{(\ell-1)/\ell}}{\ell \log(n)} \left[ \frac{1}{f^n (x_0)} - (a \ell n)^{1/\ell} \right] \\&= \lim_{n \to \infty} \frac{ a (a \ell n)^{(\ell-1)/\ell}}{\log(n)} \left[ \frac{1}{ (a \ell n)^{1/\ell}} - f^{n}(x_0) \right] \frac{(a \ell n)^{1/\ell}}{f^n(x_0)}.\end{align*} $$
Using Equation (22), one thus concludes
 $$ \begin{align*}R = \lim_{n \to \infty} \frac{ a (a \ell n)^{(\ell - 1)/\ell} (a \ell n)^{2/\ell} }{\log(n)} \left[ \frac{1}{ (a \ell n)^{1/\ell}} - f^{n}(x_0) \right] .\end{align*} $$
$$ \begin{align*}R = \lim_{n \to \infty} \frac{ a (a \ell n)^{(\ell - 1)/\ell} (a \ell n)^{2/\ell} }{\log(n)} \left[ \frac{1}{ (a \ell n)^{1/\ell}} - f^{n}(x_0) \right] .\end{align*} $$
Therefore,
 $$ \begin{align*}\mathrm{Resit} (f) = \frac{R}{a^2} = \lim_{n \to \infty} \frac{ \ell n (a \ell n)^{1/\ell} }{\log(n)} \left[ \frac{1}{ (a \ell n)^{1/\ell}} - f^{n}(x_0) \right],\end{align*} $$
$$ \begin{align*}\mathrm{Resit} (f) = \frac{R}{a^2} = \lim_{n \to \infty} \frac{ \ell n (a \ell n)^{1/\ell} }{\log(n)} \left[ \frac{1}{ (a \ell n)^{1/\ell}} - f^{n}(x_0) \right],\end{align*} $$
as announced.
It remains to show that the sequence
![]() $\varphi _n(z)$
defined by Equation (21) converges as n goes to infinity. First notice that, for all large-enough z,
$\varphi _n(z)$
defined by Equation (21) converges as n goes to infinity. First notice that, for all large-enough z,
Hence, for a fixed z and large-enough n,
Using Equation (20) and this last estimate, we obtain
 $$ \begin{align*} \varphi_{n+1} (z) - \varphi_n (z) \ &= g^{n+1} (z) -a\ell (n+1) - \frac{R \log(n+1)}{a} - \left[ g^n(z) - a\ell n - \frac{R \log(n)}{a} \right] \\ &= \left[ g^n(z) + a\ell + \frac{R \ell}{g^n(z)} + O \left(\frac{1}{g^n(z)^2} \right) \right] - a\ell - \frac{R }{a} \log \left( \frac{n+1}{n} \right) - g^n(z), \end{align*} $$
$$ \begin{align*} \varphi_{n+1} (z) - \varphi_n (z) \ &= g^{n+1} (z) -a\ell (n+1) - \frac{R \log(n+1)}{a} - \left[ g^n(z) - a\ell n - \frac{R \log(n)}{a} \right] \\ &= \left[ g^n(z) + a\ell + \frac{R \ell}{g^n(z)} + O \left(\frac{1}{g^n(z)^2} \right) \right] - a\ell - \frac{R }{a} \log \left( \frac{n+1}{n} \right) - g^n(z), \end{align*} $$
hence
 $$ \begin{align} \varphi_{n+1} (z) - \varphi_n (z) = \frac{R \ell}{g^n(z)} - \frac{R }{a} \log \left( \frac{n+1}{n} \right) + O \left(\frac{1}{g^n(z)^2} \right) = O \left( \frac{1}{n} \right). \end{align} $$
$$ \begin{align} \varphi_{n+1} (z) - \varphi_n (z) = \frac{R \ell}{g^n(z)} - \frac{R }{a} \log \left( \frac{n+1}{n} \right) + O \left(\frac{1}{g^n(z)^2} \right) = O \left( \frac{1}{n} \right). \end{align} $$
This estimate is still weak to prove the announced convergence, but reintroducing it in the computations above will give the desired convergence. Indeed, letting
![]() $\varphi _0 (z) := z$
, it yields
$\varphi _0 (z) := z$
, it yields
 $$ \begin{align*}|\varphi_n (z) - z| \leq \sum_{i=1}^n |\varphi_i (z) - \varphi_{i-1} (z)| = O (\log(n)).\end{align*} $$
$$ \begin{align*}|\varphi_n (z) - z| \leq \sum_{i=1}^n |\varphi_i (z) - \varphi_{i-1} (z)| = O (\log(n)).\end{align*} $$
Using the left-hand side equality in Equation (23), the definition of
![]() $\varphi _n$
and the latter estimate, we finally obtain
$\varphi _n$
and the latter estimate, we finally obtain
 $$ \begin{align*} \varphi_{n+1} (z) - \varphi_n (z) =\ & \frac{R \ell}{g^n(z)} - \frac{R }{a} \log \left( \frac{n+1}{n} \right) + O \left( \frac{1}{n^2} \right) \\ =\ & \frac{R \ell}{a\ell n + \varphi_n (z) + R \log(n) / a} - \frac{R}{an} + O \big( \frac{1}{n^2} \big) \\ =\ & \frac{\varphi_n (z) + R \log(n) / a}{an (a\ell n + \varphi_n (z) + R \log(n) / a)} + O \big( \frac{1}{n^2} \big) \\ =\ & O \left( \frac{\log (n)}{n^2} \right). \end{align*} $$
$$ \begin{align*} \varphi_{n+1} (z) - \varphi_n (z) =\ & \frac{R \ell}{g^n(z)} - \frac{R }{a} \log \left( \frac{n+1}{n} \right) + O \left( \frac{1}{n^2} \right) \\ =\ & \frac{R \ell}{a\ell n + \varphi_n (z) + R \log(n) / a} - \frac{R}{an} + O \big( \frac{1}{n^2} \big) \\ =\ & \frac{\varphi_n (z) + R \log(n) / a}{an (a\ell n + \varphi_n (z) + R \log(n) / a)} + O \big( \frac{1}{n^2} \big) \\ =\ & O \left( \frac{\log (n)}{n^2} \right). \end{align*} $$
Since the sum
![]() $\sum \frac {\log (n)}{ n^2}$
is finite, this shows that
$\sum \frac {\log (n)}{ n^2}$
is finite, this shows that
![]() $(\varphi _n(z))$
is a Cauchy sequence, which implies the announced convergence.
$(\varphi _n(z))$
is a Cauchy sequence, which implies the announced convergence.
Proof Second proof (using vector fields).
We know from §3.1 that the vector field X associated to f has a Taylor series expansion of the form
We compute
 $$ \begin{align*} n =\ & \int_{x_0}^{f^n(x_0)} \frac{dy}{X(y)} \\ =\ & \int_{x_0}^{f^n(x_0)}\!\! \frac{dy}{-a y^{\ell + 1} - R y^{2\ell + 1}} + \int_{x_0}^{f^n(x_0)} \!\!\left[ \frac{1}{a y^{\ell + 1} + R y^{2\ell + 1}} - \frac{1}{a y^{\ell + 1} + R y^{2\ell + 1} + o(y^{2\ell + 1})} \right] \kern-1pt dy \\ =\ & \int_{x_0}^{f^n(x_0)} \frac{dy}{-a y^{\ell + 1} (1 + R y^{\ell} /a)} + \int_{x_0}^{f^n(x_0)} \left[ \frac{o(y^{2\ell + 1})}{y^{2\ell+2} (a^2 + o(y))} \right] \, dy \\ =\ & \int_{x_0}^{f^n(x_0)} \left[ \frac{1 - Ry^{\ell}/a + o(y^{2\ell-1})}{-a y^{\ell + 1}} \right] \, dy + \int_{x_0}^{f^n(x_0)} o \left( \frac{1}{y} \right) \, dy \\ =\ & \frac{1}{a \ell y^{\ell}}\Big|^{f^n(x_0)}_{x_0} + \frac{R \, \log(y)}{a^2}\Big|^{f^n(x_0)}_{x_0} - \frac1a \int_{x_0}^{f^n (x_0)} o \left( y^{\ell-2} \right) + o (\log (f^n (x_0))) \\ =\ & \frac{1}{a \, \ell \, [f^n (x_0)]^{\ell}} + \frac{R \, \log(f^n (x_0))}{a^2} + C_{x_{0}} + o (\log (f^n(x_0))), \end{align*} $$
$$ \begin{align*} n =\ & \int_{x_0}^{f^n(x_0)} \frac{dy}{X(y)} \\ =\ & \int_{x_0}^{f^n(x_0)}\!\! \frac{dy}{-a y^{\ell + 1} - R y^{2\ell + 1}} + \int_{x_0}^{f^n(x_0)} \!\!\left[ \frac{1}{a y^{\ell + 1} + R y^{2\ell + 1}} - \frac{1}{a y^{\ell + 1} + R y^{2\ell + 1} + o(y^{2\ell + 1})} \right] \kern-1pt dy \\ =\ & \int_{x_0}^{f^n(x_0)} \frac{dy}{-a y^{\ell + 1} (1 + R y^{\ell} /a)} + \int_{x_0}^{f^n(x_0)} \left[ \frac{o(y^{2\ell + 1})}{y^{2\ell+2} (a^2 + o(y))} \right] \, dy \\ =\ & \int_{x_0}^{f^n(x_0)} \left[ \frac{1 - Ry^{\ell}/a + o(y^{2\ell-1})}{-a y^{\ell + 1}} \right] \, dy + \int_{x_0}^{f^n(x_0)} o \left( \frac{1}{y} \right) \, dy \\ =\ & \frac{1}{a \ell y^{\ell}}\Big|^{f^n(x_0)}_{x_0} + \frac{R \, \log(y)}{a^2}\Big|^{f^n(x_0)}_{x_0} - \frac1a \int_{x_0}^{f^n (x_0)} o \left( y^{\ell-2} \right) + o (\log (f^n (x_0))) \\ =\ & \frac{1}{a \, \ell \, [f^n (x_0)]^{\ell}} + \frac{R \, \log(f^n (x_0))}{a^2} + C_{x_{0}} + o (\log (f^n(x_0))), \end{align*} $$
where
![]() $C_{x_0}$
is a constant that depends only on
$C_{x_0}$
is a constant that depends only on
![]() $x_0$
(and is independent of n). The right-side expression is of the form
$x_0$
(and is independent of n). The right-side expression is of the form
 $$ \begin{align*}\frac{1}{a \, \ell \, [f^n (x_0)]^{\ell}} + o \left( \frac{1}{[f^n(x_0)]^\ell} \right),\end{align*} $$
$$ \begin{align*}\frac{1}{a \, \ell \, [f^n (x_0)]^{\ell}} + o \left( \frac{1}{[f^n(x_0)]^\ell} \right),\end{align*} $$
which shows that, as n goes to infinity,
Now, from
 $$ \begin{align*} R =\ & \frac{a^2 \, (n-C_{x_0})}{\log (f^n (x_0))} - \frac{a}{\ell \, [f^n(x_0)]^\ell \, \log (f^n(x_0))} + o(1) \\ =\ & \frac{a^2 \, (n-C_{x_0})}{[f^n(x_0)]^\ell \, \log (f^n(x_0))} \left[ [f^n(x_0)]^\ell - \frac{1}{a \, \ell \, (n-C_{x_0})} \right] + o(1), \end{align*} $$
$$ \begin{align*} R =\ & \frac{a^2 \, (n-C_{x_0})}{\log (f^n (x_0))} - \frac{a}{\ell \, [f^n(x_0)]^\ell \, \log (f^n(x_0))} + o(1) \\ =\ & \frac{a^2 \, (n-C_{x_0})}{[f^n(x_0)]^\ell \, \log (f^n(x_0))} \left[ [f^n(x_0)]^\ell - \frac{1}{a \, \ell \, (n-C_{x_0})} \right] + o(1), \end{align*} $$
using Equation (24) we obtain
 $$ \begin{align*}R = \lim_{n \to \infty} \frac{a^2 \, (n-C_{x_0})}{\frac{1}{a \, \ell \, n} \cdot \frac{1}{\ell}\log (\frac{1}{a \, \ell \, n})} \left[ [f^n(x_0) ]^\ell - \frac{1}{a \, \ell \, (n-C_{x_0})} \right] = \lim_{n \to \infty} \frac{a^3 \, \ell^2 \, n^2}{\log(n)} \left[ \frac{1}{a \, \ell \, n} - [f^n (x_0)]^\ell \right].\end{align*} $$
$$ \begin{align*}R = \lim_{n \to \infty} \frac{a^2 \, (n-C_{x_0})}{\frac{1}{a \, \ell \, n} \cdot \frac{1}{\ell}\log (\frac{1}{a \, \ell \, n})} \left[ [f^n(x_0) ]^\ell - \frac{1}{a \, \ell \, (n-C_{x_0})} \right] = \lim_{n \to \infty} \frac{a^3 \, \ell^2 \, n^2}{\log(n)} \left[ \frac{1}{a \, \ell \, n} - [f^n (x_0)]^\ell \right].\end{align*} $$
Therefore,
 $$ \begin{align*}\mathrm{Resit}(f) = \frac{R}{a^2} = \lim_{n \to \infty} \frac{a \, \ell^2 \, n^2}{\log(n)} \left[ \frac{1}{a \, \ell \, n} - [ f^n (x_0) ]^\ell \right] = \lim_{n \to \infty} \left[ \frac{ \ell \, n \sqrt[\ell]{a \ell n}}{\log (n)} \left( \frac{1}{ \sqrt[\ell]{a \, \ell \, n}} - f^n (x_0)\right) \right],\end{align*} $$
$$ \begin{align*}\mathrm{Resit}(f) = \frac{R}{a^2} = \lim_{n \to \infty} \frac{a \, \ell^2 \, n^2}{\log(n)} \left[ \frac{1}{a \, \ell \, n} - [ f^n (x_0) ]^\ell \right] = \lim_{n \to \infty} \left[ \frac{ \ell \, n \sqrt[\ell]{a \ell n}}{\log (n)} \left( \frac{1}{ \sqrt[\ell]{a \, \ell \, n}} - f^n (x_0)\right) \right],\end{align*} $$
where the last equality follows from the identity
![]() $u^\ell - v^\ell = (u-v) (u^{\ell -1} + u^{\ell -2}v + \ldots + v^{\ell -1})$
.
$u^\ell - v^\ell = (u-v) (u^{\ell -1} + u^{\ell -2}v + \ldots + v^{\ell -1})$
.
Remark 3.3. It is a nice exercise to deduce the general case of the previous proposition from the case
![]() $\ell =1$
via conjugacy by the map
$\ell =1$
via conjugacy by the map
![]() $x \mapsto x^{\ell }$
; see Remark 1.6.
$x \mapsto x^{\ell }$
; see Remark 1.6.
What follows is a direct consequence of the previous proposition; checking the details is left to the reader. It is worth comparing the case
![]() $\ell =1$
of the statement with (11).
$\ell =1$
of the statement with (11).
Corollary 3.4. If
![]() $\ell \geq 1$
, then, for every contracting germ
$\ell \geq 1$
, then, for every contracting germ
![]() $f \in \mathrm {Diff}^{2\ell + 1}_\ell (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
of the form
$f \in \mathrm {Diff}^{2\ell + 1}_\ell (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
of the form
and all
![]() $x_0> 0$
, one has
$x_0> 0$
, one has
 $$ \begin{align} f^n (x_0) = \frac{1}{\sqrt[\ell]{a \ell n}} \left( 1 - \frac{[\mathrm{Resit}(f) + \delta_n] \log (n)}{\ell \, n} \right), \end{align} $$
$$ \begin{align} f^n (x_0) = \frac{1}{\sqrt[\ell]{a \ell n}} \left( 1 - \frac{[\mathrm{Resit}(f) + \delta_n] \log (n)}{\ell \, n} \right), \end{align} $$
where
![]() $\delta _n$
is a sequence that converges to
$\delta _n$
is a sequence that converges to
![]() $0$
as n goes to infinity.
$0$
as n goes to infinity.
3.4 A second proof of the
 $C^{\ell + 1}$
conjugacy invariance of
$C^{\ell + 1}$
conjugacy invariance of
 $\mathrm {Resit}$
$\mathrm {Resit}$
We can give an alternative proof of Theorem A using the estimates of the previous section.
Proof Second proof of Theorem A
Let
![]() $f,g$
in
$f,g$
in
![]() $\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
be elements conjugated by
$\mathrm {Diff}^{2\ell + 1}_{\ell } (\mathbb {R},0) \setminus \mathrm {Diff}^{2\ell + 1}_{\ell + 1} (\mathbb {R},0)$
be elements conjugated by
![]() $h \in \mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
. In order to show that
$h \in \mathrm {Diff}^{\ell + 1}_+ (\mathbb {R},0)$
. In order to show that
![]() $\mathrm {Resit} (f)$
and
$\mathrm {Resit} (f)$
and
![]() $\mathrm {Resit} (g)$
coincide, we may assume that f and g have Taylor series expansions at the origin of the form
$\mathrm {Resit} (g)$
coincide, we may assume that f and g have Taylor series expansions at the origin of the form
The very same arguments of the beginning of the first proof show that h must write in the form
In particular, for a certain constant
![]() $C> 0$
,
$C> 0$
,
for all small-enough
![]() $x> 0$
. Fix such an
$x> 0$
. Fix such an
![]() $x_0> 0$
. From
$x_0> 0$
. From
![]() $hf = gh$
, we obtain
$hf = gh$
, we obtain
![]() $hf^n (x_0) = g^n h(x_0)$
for all n, which yields
$hf^n (x_0) = g^n h(x_0)$
for all n, which yields
Using Equations (25) and (26), this implies
 $$ \begin{align} C \left[ \frac{1}{\sqrt[\ell]{a\ell n}} \left( 1 - \frac{[\mathrm{Resit} (f) + \delta_n] \log (n)}{\ell \, n} \right) \right]^{\ell + 1} \geq \left| \frac{[\mathrm{Resit}(g) - \mathrm{Resit}(f) + \delta_n'] \log (n)}{\ell \, n \, \sqrt[\ell]{a \ell n}} \right| \end{align} $$
$$ \begin{align} C \left[ \frac{1}{\sqrt[\ell]{a\ell n}} \left( 1 - \frac{[\mathrm{Resit} (f) + \delta_n] \log (n)}{\ell \, n} \right) \right]^{\ell + 1} \geq \left| \frac{[\mathrm{Resit}(g) - \mathrm{Resit}(f) + \delta_n'] \log (n)}{\ell \, n \, \sqrt[\ell]{a \ell n}} \right| \end{align} $$
for certain sequences
![]() $\delta _n,\delta _n'$
converging to
$\delta _n,\delta _n'$
converging to
![]() $0$
. On the one hand, the left-hand term above is of order
$0$
. On the one hand, the left-hand term above is of order
![]() $1/ (n \, \sqrt [\ell ]{n})$
. On the other hand, if
$1/ (n \, \sqrt [\ell ]{n})$
. On the other hand, if
![]() $\mathrm {Resit}(f) \neq \mathrm {Resit}(g)$
, then the right-hand term is of order
$\mathrm {Resit}(f) \neq \mathrm {Resit}(g)$
, then the right-hand term is of order
Therefore, if
![]() $\mathrm {Resit}(f) \neq \mathrm {Resit}(g)$
, then inequality (27) is impossible for large-enough n. Thus,
$\mathrm {Resit}(f) \neq \mathrm {Resit}(g)$
, then inequality (27) is impossible for large-enough n. Thus,
![]() $\mathrm {Resit}(f)$
and
$\mathrm {Resit}(f)$
and
![]() $\mathrm {Resit}(g)$
must coincide in case of
$\mathrm {Resit}(g)$
must coincide in case of
![]() $C^{\ell + 1}$
conjugacy.
$C^{\ell + 1}$
conjugacy.
4 Existence of low regular conjugacies between germs
The goal of this section is to prove Theorem B’, of which Theorem B is a particular case (namely, the case
![]() $r = \ell $
). To begin with, notice that, passing to inverses if necessary, we may assume that the diffeomorphisms in consideration are both expanding. Looking at the associated vector fields, one readily checks that Theorem B’ is a direct consequence of the next proposition. For the statement, given
$r = \ell $
). To begin with, notice that, passing to inverses if necessary, we may assume that the diffeomorphisms in consideration are both expanding. Looking at the associated vector fields, one readily checks that Theorem B’ is a direct consequence of the next proposition. For the statement, given
![]() $\ell \geq 1$
, we say that a (germ of) vector field Z is exactly
$\ell \geq 1$
, we say that a (germ of) vector field Z is exactly
![]() $\ell $
-flat if it has a Taylor series expansion at the origin of the form
$\ell $
-flat if it has a Taylor series expansion at the origin of the form
Proposition 4.1. Given
![]() $\ell \ge 1$
and
$\ell \ge 1$
and
![]() $1\le r\le \ell $
, any two germs at
$1\le r\le \ell $
, any two germs at
![]() $0$
of exactly
$0$
of exactly
![]() $\ell $
-flat, expanding
$\ell $
-flat, expanding
![]() $C^{\ell +r}$
vector fields are
$C^{\ell +r}$
vector fields are
![]() $C^{r}$
conjugate.
$C^{r}$
conjugate.
For
![]() $r=1$
, this is a result concerning
$r=1$
, this is a result concerning
![]() $C^1$
conjugacies between vector fields that should be compared to Proposition 2.1, yet the hypothesis here are much stronger.
$C^1$
conjugacies between vector fields that should be compared to Proposition 2.1, yet the hypothesis here are much stronger.
Remark 4.2. The conjugacy is no better than
![]() $C^{r}$
in general. For instance, in §2.3 there is an example of germs of exactly 1-flat, expanding,
$C^{r}$
in general. For instance, in §2.3 there is an example of germs of exactly 1-flat, expanding,
![]() $C^3$
vector fields (case
$C^3$
vector fields (case
![]() $\ell =1,\ r=1$
) that are
$\ell =1,\ r=1$
) that are
![]() $C^1$
conjugate but not
$C^1$
conjugate but not
![]() $C^2$
conjugate, despite the time-1 maps have the same (actually, vanishing) iterative residue. It would be interesting to exhibit examples showing that the proposition is optimal for all the cases it covers.
$C^2$
conjugate, despite the time-1 maps have the same (actually, vanishing) iterative residue. It would be interesting to exhibit examples showing that the proposition is optimal for all the cases it covers.
To prove Proposition 4.1, we will use a well-known general lemma concerning reduced forms for vector fields that is a kind of simpler version of [Reference Takens21, Proposition 2.3] in finite regularity. (Compare Lemma 1.3, which deals with the case of diffeomorphisms.)
Lemma 4.3. Let
![]() $\ell \geq 1$
and
$\ell \geq 1$
and
![]() $r \geq 1$
, and let Y be a germ of
$r \geq 1$
, and let Y be a germ of
![]() $C^{\ell + r}$
vector field admitting a Taylor series expansion of order
$C^{\ell + r}$
vector field admitting a Taylor series expansion of order
![]() $\ell + r$
at the origin that starts with
$\ell + r$
at the origin that starts with
![]() $\alpha x^{\ell +1}$
, where
$\alpha x^{\ell +1}$
, where
![]() $\alpha> 0$
. If
$\alpha> 0$
. If
![]() $1\le r \le \ell $
, then Y is
$1\le r \le \ell $
, then Y is
![]() $C^{\infty }$
conjugate to a vector field of the form
$C^{\infty }$
conjugate to a vector field of the form
![]() $x\mapsto x^{\ell +1}+o(x^{\ell +r})$
.
$x\mapsto x^{\ell +1}+o(x^{\ell +r})$
.
Proof. For
![]() $1\le r \le \ell $
, we construct by induction a sequence of
$1\le r \le \ell $
, we construct by induction a sequence of
![]() $C^\infty $
conjugates
$C^\infty $
conjugates
![]() $Y_1$
, …,
$Y_1$
, …,
![]() $Y_r$
of Y such that
$Y_r$
of Y such that
![]() $Y_s(x)=x^{\ell +1}+o(x^{\ell +s})$
for every
$Y_s(x)=x^{\ell +1}+o(x^{\ell +s})$
for every
![]() $s \in [\![1,r]\!] := \{1,2,\ldots ,r\}$
. One first obtains
$s \in [\![1,r]\!] := \{1,2,\ldots ,r\}$
. One first obtains
![]() $Y_1$
by conjugating Y by a homothety. Assume we have constructed
$Y_1$
by conjugating Y by a homothety. Assume we have constructed
![]() $Y_s$
for some
$Y_s$
for some
![]() $s \in [\![1,r-1]\!]$
, and consider the diffeomorphism
$s \in [\![1,r-1]\!]$
, and consider the diffeomorphism
![]() $h(x)=x+ax^{s+1}$
. Since
$h(x)=x+ax^{s+1}$
. Since
![]() $Y_s$
is
$Y_s$
is
![]() $C^{\ell +s+1}$
, there exists
$C^{\ell +s+1}$
, there exists
![]() $\alpha \in \mathbb {R}$
such that
$\alpha \in \mathbb {R}$
such that
![]() $Y_s(x) = x^{\ell + 1}+\alpha _s x^{\ell +s+1} + o(x^{\ell +s+1})$
. Then, for
$Y_s(x) = x^{\ell + 1}+\alpha _s x^{\ell +s+1} + o(x^{\ell +s+1})$
. Then, for
![]() $Y_{s+1}(x) := h^* Y_s(x) = \frac {Y_s(h(x))}{Dh(x)}$
, we have
$Y_{s+1}(x) := h^* Y_s(x) = \frac {Y_s(h(x))}{Dh(x)}$
, we have
 $$ \begin{align*} Y_{s+1}(x) =\ & \frac{(h(x))^{\ell+1}+\alpha_s (h(x))^{\ell +s+1}+o((h(x))^{\ell +s+1})}{1+a(s+1)x^{s}}\\ =\ & \frac{(x+ax^{s+1})^{\ell+1}+\alpha_s (x+ax^{s+1})^{\ell +s+1}+o(x^{\ell+s+1})}{1+a(s+1)x^{s}}\\ =\ & \left(x^{\ell +1}+((\ell+1)a+\alpha_s)x^{\ell +s+1}+o(x^{\ell +s+1})\right)\left(1-a(s+1)x^{s}+o(x^{s})\right)\\ =\ & x^{\ell+1}+\left((\ell - s)a+\alpha_s \right)x^{\ell+s+1}+o(x^{\ell +s+1}). \end{align*} $$
$$ \begin{align*} Y_{s+1}(x) =\ & \frac{(h(x))^{\ell+1}+\alpha_s (h(x))^{\ell +s+1}+o((h(x))^{\ell +s+1})}{1+a(s+1)x^{s}}\\ =\ & \frac{(x+ax^{s+1})^{\ell+1}+\alpha_s (x+ax^{s+1})^{\ell +s+1}+o(x^{\ell+s+1})}{1+a(s+1)x^{s}}\\ =\ & \left(x^{\ell +1}+((\ell+1)a+\alpha_s)x^{\ell +s+1}+o(x^{\ell +s+1})\right)\left(1-a(s+1)x^{s}+o(x^{s})\right)\\ =\ & x^{\ell+1}+\left((\ell - s)a+\alpha_s \right)x^{\ell+s+1}+o(x^{\ell +s+1}). \end{align*} $$
Since
![]() $s \leq r-1 < \ell $
, we may let
$s \leq r-1 < \ell $
, we may let
![]() $a := \frac {\alpha _s}{s-\ell }$
to obtain
$a := \frac {\alpha _s}{s-\ell }$
to obtain
![]() $Y_{s+1}(x) = x^{\ell +1}+o(x^{\ell +s+1})$
, which concludes the induction and thus finishes the proof. Observe that the conjugacy that arises at the end of the inductive process is a germ of polynomial diffeomorphism.
$Y_{s+1}(x) = x^{\ell +1}+o(x^{\ell +s+1})$
, which concludes the induction and thus finishes the proof. Observe that the conjugacy that arises at the end of the inductive process is a germ of polynomial diffeomorphism.
We will also need a couple of elementary technical lemmas. For the statement, in analogy to the case of vector fields, we say that a real-valued function u is
![]() $\ell $
-flat at
$\ell $
-flat at
![]() $0$
if it has a Taylor series expansion at the origin of the form
$0$
if it has a Taylor series expansion at the origin of the form
![]() $u(x) = a x^{\ell +1} + o (x^{\ell +1}).$
$u(x) = a x^{\ell +1} + o (x^{\ell +1}).$
Lemma 4.4. If u is a
![]() $C^{k}$
germ of m-flat function at
$C^{k}$
germ of m-flat function at
![]() $0$
, with
$0$
, with
![]() $0 \leq m < k$
, then
$0 \leq m < k$
, then
![]() $x\mapsto \frac {u(x)}{x^{m+1}}$
extends at
$x\mapsto \frac {u(x)}{x^{m+1}}$
extends at
![]() $0$
to a germ of
$0$
to a germ of
![]() $C^{k-m-1}$
map.
$C^{k-m-1}$
map.
Proof. Since u is of class
![]() $C^{k}$
and m-flat, all its derivatives at the origin up to order m must vanish. Hence, since u is of class
$C^{k}$
and m-flat, all its derivatives at the origin up to order m must vanish. Hence, since u is of class
![]() $C^{m+1}$
, we have the following form of Taylor’s formula:
$C^{m+1}$
, we have the following form of Taylor’s formula:
 $$ \begin{align*}u(x) = 0+0\cdot x +\dots + 0\cdot x^m +\frac{x^{m+1}}{m \, !} \int_0^1(1-t)^m D^{(m+1)} u(tx)dt. \end{align*} $$
$$ \begin{align*}u(x) = 0+0\cdot x +\dots + 0\cdot x^m +\frac{x^{m+1}}{m \, !} \int_0^1(1-t)^m D^{(m+1)} u(tx)dt. \end{align*} $$
The lemma then follows by differentiating under the integral.
Lemma 4.5. Let
![]() $r\ge 1$
, and let
$r\ge 1$
, and let
![]() $\varphi $
be a germ of continuous function at the origin that is differentiable outside
$\varphi $
be a germ of continuous function at the origin that is differentiable outside
![]() $0$
and such that
$0$
and such that
![]() $\varphi (0)=1$
. If
$\varphi (0)=1$
. If
![]() $x\mapsto x \, \varphi (x)$
is of class
$x\mapsto x \, \varphi (x)$
is of class
![]() $C^r$
, so is the function
$C^r$
, so is the function
![]() $x\mapsto x \, (\varphi (x))^\vartheta $
for any
$x\mapsto x \, (\varphi (x))^\vartheta $
for any
![]() $\vartheta \neq 0$
.
$\vartheta \neq 0$
.
Proof. Let
![]() $u(x) := x \, \varphi (x)$
and
$u(x) := x \, \varphi (x)$
and
![]() $v(x) := x \, (\varphi (x))^\vartheta $
. Assume u is of class
$v(x) := x \, (\varphi (x))^\vartheta $
. Assume u is of class
![]() $C^r$
. If
$C^r$
. If
![]() $\vartheta = 1$
, there is nothing to prove, so let us assume
$\vartheta = 1$
, there is nothing to prove, so let us assume
![]() $\vartheta \neq 1$
. By Lemma 4.4,
$\vartheta \neq 1$
. By Lemma 4.4,
![]() $\varphi $
is
$\varphi $
is
![]() $C^{r-1}$
. Now, outside
$C^{r-1}$
. Now, outside
![]() $0$
,
$0$
,
By the first equality, since
![]() $Du$
and
$Du$
and
![]() $\varphi $
are
$\varphi $
are
![]() $C^{r-1}$
so is
$C^{r-1}$
so is
![]() $x\mapsto x \, D \varphi (x)$
. Thus, by the second equality,
$x\mapsto x \, D \varphi (x)$
. Thus, by the second equality,
![]() $Dv$
writes as a sum of products and compositions of
$Dv$
writes as a sum of products and compositions of
![]() $C^{r-1}$
maps, hence it is
$C^{r-1}$
maps, hence it is
![]() $C^{r-1}$
. Therefore, v is
$C^{r-1}$
. Therefore, v is
![]() $C^r$
, as announced.
$C^r$
, as announced.
Proof Proof of Theorem B’
Let f be an expanding germ in
![]() $\mathrm {Diff}^{\ell + 1 + r}_+(\mathbb {R},0)$
that is exactly
$\mathrm {Diff}^{\ell + 1 + r}_+(\mathbb {R},0)$
that is exactly
![]() $\ell $
-tangent to the identity, and let X be its associated
$\ell $
-tangent to the identity, and let X be its associated
![]() $C^{\ell + r}$
vector field. We will show that X is
$C^{\ell + r}$
vector field. We will show that X is
![]() $C^r$
conjugate to
$C^r$
conjugate to
![]() $X_{\ell }(x):=x^{\ell +1}$
. This allows concluding the proof. Indeed, if g is another expanding germ in
$X_{\ell }(x):=x^{\ell +1}$
. This allows concluding the proof. Indeed, if g is another expanding germ in
![]() $\mathrm {Diff}^{\ell + 1 + r}_+(\mathbb {R},0)$
that is exactly
$\mathrm {Diff}^{\ell + 1 + r}_+(\mathbb {R},0)$
that is exactly
![]() $\ell $
-tangent to the identity, then its associated vector field Y will also be
$\ell $
-tangent to the identity, then its associated vector field Y will also be
![]() $C^r$
conjugate to
$C^r$
conjugate to
![]() $X_{\ell }$
. Therefore, X and Y will be
$X_{\ell }$
. Therefore, X and Y will be
![]() $C^r$
conjugate, and this will allow conjugating their time-1 maps, that is, f and g.
$C^r$
conjugate, and this will allow conjugating their time-1 maps, that is, f and g.
Now, by Lemma 4.3, we may assume that
![]() $X(x)=x^{\ell +1}(1+\delta (x))$
with
$X(x)=x^{\ell +1}(1+\delta (x))$
with
![]() $\delta (x)=o(x^{r-1})$
. Moreover, by Lemma 4.4 (applied to
$\delta (x)=o(x^{r-1})$
. Moreover, by Lemma 4.4 (applied to
![]() $k = \ell + r$
and
$k = \ell + r$
and
![]() $m = \ell $
), we may also assume that
$m = \ell $
), we may also assume that
![]() $\delta $
is of class
$\delta $
is of class
![]() $C^{r-1}$
. Equivalently, we can write
$C^{r-1}$
. Equivalently, we can write
![]() $X(x)= \frac {x^{\ell +1}}{1+\epsilon (x)}$
, still with
$X(x)= \frac {x^{\ell +1}}{1+\epsilon (x)}$
, still with
![]() $\epsilon $
of class
$\epsilon $
of class
![]() $C^{r-1}$
and
$C^{r-1}$
and
![]() $(r-1)$
-flat. To prove that X is
$(r-1)$
-flat. To prove that X is
![]() $C^{r}$
conjugate to
$C^{r}$
conjugate to
![]() $X_\ell $
, it suffices to prove that the solutions h of
$X_\ell $
, it suffices to prove that the solutions h of
![]() $Dh=X_\ell \circ h / X$
on
$Dh=X_\ell \circ h / X$
on
![]() $\mathbb {R}_+^*$
(near
$\mathbb {R}_+^*$
(near
![]() $0$
), which are of class
$0$
), which are of class
![]() $C^{\ell +r+1}$
, extend to
$C^{\ell +r+1}$
, extend to
![]() $C^{r}$
diffeomorphisms at the origin. Assume without loss of generality that X is expanding on an interval containing the origin and
$C^{r}$
diffeomorphisms at the origin. Assume without loss of generality that X is expanding on an interval containing the origin and
![]() $1$
, and consider the solution h fixing
$1$
, and consider the solution h fixing
![]() $1$
. We have
$1$
. We have
 $$ \begin{align*}\int_1^{h(x)}\frac{1}{X_{\ell}} = \int_1^{x}\frac{Dh}{X_\ell \circ h}=\int_1^x \frac1X,\end{align*} $$
$$ \begin{align*}\int_1^{h(x)}\frac{1}{X_{\ell}} = \int_1^{x}\frac{Dh}{X_\ell \circ h}=\int_1^x \frac1X,\end{align*} $$
that is
 $$ \begin{align*}-\frac1{\ell \, (h(x))^\ell} = -\frac1{\ell \, x^\ell} + \int_1^x\frac{\epsilon(y)}{y^{\ell+1}}dy+c\end{align*} $$
$$ \begin{align*}-\frac1{\ell \, (h(x))^\ell} = -\frac1{\ell \, x^\ell} + \int_1^x\frac{\epsilon(y)}{y^{\ell+1}}dy+c\end{align*} $$
for some constant c. Equivalently,
 $$ \begin{align*}\frac1{(h(x))^\ell} = \frac1{x^\ell} - \ell \, u(x), \quad \mbox{ with }\quad u(x)=\int_1^x\frac{\epsilon(y)}{y^{\ell +1}}dy+c.\end{align*} $$
$$ \begin{align*}\frac1{(h(x))^\ell} = \frac1{x^\ell} - \ell \, u(x), \quad \mbox{ with }\quad u(x)=\int_1^x\frac{\epsilon(y)}{y^{\ell +1}}dy+c.\end{align*} $$
This implies
 $$ \begin{align*}{(h(x))^\ell} = \frac1{\frac1{x^\ell}(1-\ell \, x^\ell \, u(x))} = \frac{x^\ell}{1-\ell \, x^\ell \, u(x)} \end{align*} $$
$$ \begin{align*}{(h(x))^\ell} = \frac1{\frac1{x^\ell}(1-\ell \, x^\ell \, u(x))} = \frac{x^\ell}{1-\ell \, x^\ell \, u(x)} \end{align*} $$
so that
Recall that
![]() $\epsilon $
is
$\epsilon $
is
![]() $C^{r-1}$
, so u is
$C^{r-1}$
, so u is
![]() $C^{r}$
outside
$C^{r}$
outside
![]() $0$
. Moreover,
$0$
. Moreover,
![]() $\epsilon $
is
$\epsilon $
is
![]() $(r-1)$
-flat, so
$(r-1)$
-flat, so
![]() $\frac {\epsilon (y)}{y^{\ell +1}} =o(y^{r-\ell -2})$
, and therefore, since
$\frac {\epsilon (y)}{y^{\ell +1}} =o(y^{r-\ell -2})$
, and therefore, since
![]() $r \leq \ell $
,
$r \leq \ell $
,
In particular,
![]() $x^\ell u(x)\to 0$
as
$x^\ell u(x)\to 0$
as
![]() $x \to 0$
since
$x \to 0$
since
![]() $r\ge 1$
. According to Lemma 4.5, it thus suffices to prove that
$r\ge 1$
. According to Lemma 4.5, it thus suffices to prove that
![]() $x\mapsto x(1-\ell \, x^\ell \, u(x))$
, or equivalently
$x\mapsto x(1-\ell \, x^\ell \, u(x))$
, or equivalently
![]() $v:x\mapsto x^{\ell +1} \, u(x)$
, is
$v:x\mapsto x^{\ell +1} \, u(x)$
, is
![]() $C^{r}$
. To do this, observe that
$C^{r}$
. To do this, observe that
We already know that
![]() $\epsilon $
is
$\epsilon $
is
![]() $C^{r-1}$
, so we need only check that
$C^{r-1}$
, so we need only check that
![]() $w:x\mapsto x^\ell u(x)$
is
$w:x\mapsto x^\ell u(x)$
is
![]() $C^{r-1}$
. On
$C^{r-1}$
. On
![]() $\mathbb {R}_+^*$
, w is
$\mathbb {R}_+^*$
, w is
![]() $C^{r}$
(as u) and satisfies
$C^{r}$
(as u) and satisfies
 $$ \begin{align*}D^{(r-1)}w (x) = \sum_{n=0}^{r-1}a_n x^{\ell-(r-1-n)} D^{(n)}u (x) = \sum_{n=0}^{r}a_n x^{\ell -r+1+n} D^{(n)}u (x)\end{align*} $$
$$ \begin{align*}D^{(r-1)}w (x) = \sum_{n=0}^{r-1}a_n x^{\ell-(r-1-n)} D^{(n)}u (x) = \sum_{n=0}^{r}a_n x^{\ell -r+1+n} D^{(n)}u (x)\end{align*} $$
for some constants
![]() $a_n$
. In view of this, it suffices to check that
$a_n$
. In view of this, it suffices to check that
![]() $x^{n+\ell +1-r} D^{(n)} u (x)$
has a limit at
$x^{n+\ell +1-r} D^{(n)} u (x)$
has a limit at
![]() $0$
for every n between
$0$
for every n between
![]() $0$
and
$0$
and
![]() $r-1$
. We have already checked this for
$r-1$
. We have already checked this for
![]() $n=0$
(see Equation (28) above). For
$n=0$
(see Equation (28) above). For
![]() $n\ge 1$
,
$n\ge 1$
,
 $$ \begin{align*} x^{n+\ell +1-r} D^{(n)} u (x) =\ & x^{n+\ell +1-r} \, D^{(n-1)} \! \left( \frac{\epsilon(x)}{x^{\ell +1}} \right) (x)\\ =\ & x^{n+\ell +1-r}\sum_{j=0}^{n-1} c_{n,j} \, x^{-\ell-1-(n-1-j)} D^{(j)} \epsilon (x)\\ =\ & \sum_{j=0}^{n-1}c_{n,j} \, x^{j-r+1} D^{(j)} \epsilon (x) \end{align*} $$
$$ \begin{align*} x^{n+\ell +1-r} D^{(n)} u (x) =\ & x^{n+\ell +1-r} \, D^{(n-1)} \! \left( \frac{\epsilon(x)}{x^{\ell +1}} \right) (x)\\ =\ & x^{n+\ell +1-r}\sum_{j=0}^{n-1} c_{n,j} \, x^{-\ell-1-(n-1-j)} D^{(j)} \epsilon (x)\\ =\ & \sum_{j=0}^{n-1}c_{n,j} \, x^{j-r+1} D^{(j)} \epsilon (x) \end{align*} $$
for certain constants
![]() $c_{n,j}$
. Finally, since
$c_{n,j}$
. Finally, since
![]() $\epsilon $
is
$\epsilon $
is
![]() $(r-1)$
-flat, we have
$(r-1)$
-flat, we have
![]() $D^{(j)} \epsilon (x)=o(x^{r-1-j})$
for
$D^{(j)} \epsilon (x)=o(x^{r-1-j})$
for
![]() $j\le r-1$
, which allows showing that
$j\le r-1$
, which allows showing that
![]() $x^{n+\ell +1-r} D^{(n)} u (x) \to 0$
as
$x^{n+\ell +1-r} D^{(n)} u (x) \to 0$
as
![]() $x \to 0$
, thus completing the proof.
$x \to 0$
, thus completing the proof.
5 Conjugacies in case of coincidence of residues
The goal of this section is to prove Theorem C. Again, passing to the associated vector fields, this will follow from the next proposition:
Proposition 5.1. If
![]() $\ell \geq 1$
and
$\ell \geq 1$
and
![]() $r\ge \ell +2$
, then every germ of
$r\ge \ell +2$
, then every germ of
![]() $C^{\ell +r}$
expanding vector field that is exactly
$C^{\ell +r}$
expanding vector field that is exactly
![]() $\ell $
-flat is
$\ell $
-flat is
![]() $C^{r}$
conjugate to a (unique) vector field of the form
$C^{r}$
conjugate to a (unique) vector field of the form
![]() $x\mapsto x^{\ell +1}+\mu x^{2\ell +1}$
. This still holds for
$x\mapsto x^{\ell +1}+\mu x^{2\ell +1}$
. This still holds for
![]() $r=\ell +1$
if one further assumes that the vector field has
$r=\ell +1$
if one further assumes that the vector field has
![]() $(2\ell +2)$
derivatives at
$(2\ell +2)$
derivatives at
![]() $0$
(and is not only of class
$0$
(and is not only of class
![]() $C^{2\ell +1}$
).
$C^{2\ell +1}$
).
Remark 5.2. In the case
![]() $r=\ell +1$
, the hypothesis of existence of
$r=\ell +1$
, the hypothesis of existence of
![]() $(2\ell +2)$
derivatives at the origin is necessary. Indeed, in §2.3, there is an example of a
$(2\ell +2)$
derivatives at the origin is necessary. Indeed, in §2.3, there is an example of a
![]() $1$
-flat
$1$
-flat
![]() $C^3$
vector field that is not
$C^3$
vector field that is not
![]() $C^2$
conjugate to its normal form; this provides a counterexample for
$C^2$
conjugate to its normal form; this provides a counterexample for
![]() $\ell =1$
and
$\ell =1$
and
![]() $r=2=\ell +1$
.
$r=2=\ell +1$
.
Proof Proof of Theorem C from Proposition 5.1.
Let f and g be two expanding germs as in the theorem, and let X and Y be their associated vector fields. By Proposition 5.1, these are
![]() $C^r$
conjugate to some
$C^r$
conjugate to some
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
of the form
$Y_0$
of the form
![]() $x\mapsto x^{\ell +1}+\mu x^{2\ell +1}$
and
$x\mapsto x^{\ell +1}+\mu x^{2\ell +1}$
and
![]() $x\mapsto x^{\ell +1}+\nu x^{2\ell +1}$
, respectively. Now, according to §3.1 and the hypothesis of coincidence of residues,
$x\mapsto x^{\ell +1}+\nu x^{2\ell +1}$
, respectively. Now, according to §3.1 and the hypothesis of coincidence of residues,
Thus,
![]() $X_0 = Y_0$
and, therefore, X and Y are
$X_0 = Y_0$
and, therefore, X and Y are
![]() $C^r$
conjugate, and so f and g as well.
$C^r$
conjugate, and so f and g as well.
To prove Proposition 5.1, we first need a version of Lemma 4.3 for large derivatives.
Lemma 5.3. Let
![]() $\ell \geq 1$
and
$\ell \geq 1$
and
![]() $r \geq 1$
, and let Y be a germ of
$r \geq 1$
, and let Y be a germ of
![]() $C^{\ell + r}$
vector field admitting a Taylor series expansion of order
$C^{\ell + r}$
vector field admitting a Taylor series expansion of order
![]() $\ell + r$
at the origin that starts with
$\ell + r$
at the origin that starts with
![]() $\alpha x^{\ell +1}$
, where
$\alpha x^{\ell +1}$
, where
![]() $\alpha> 0$
. If
$\alpha> 0$
. If
![]() $r \ge \ell +1$
, then Y is smoothly conjugate to a vector field of the form
$r \ge \ell +1$
, then Y is smoothly conjugate to a vector field of the form
![]() $x\mapsto x^{\ell +1}+\mu x^{2\ell +1}+o(x^{\ell + r})$
.
$x\mapsto x^{\ell +1}+\mu x^{2\ell +1}+o(x^{\ell + r})$
.
Proof. Thanks to Lemma 4.3, we can start with Y of the form
![]() $Y(x) = x^{\ell +1}+ o(x^{2\ell })$
, which can be rewritten in the form
$Y(x) = x^{\ell +1}+ o(x^{2\ell })$
, which can be rewritten in the form
![]() $Y(x) = x\mapsto x^{\ell +1}+\mu x^{2\ell +1}+ o(x^{2\ell +1})$
since Y is of class
$Y(x) = x\mapsto x^{\ell +1}+\mu x^{2\ell +1}+ o(x^{2\ell +1})$
since Y is of class
![]() $C^{2\ell +1}$
. One then constructs conjugate vector fields
$C^{2\ell +1}$
. One then constructs conjugate vector fields
![]() $Y_\ell :=Y, \ldots , Y_{r-1}$
such that each
$Y_\ell :=Y, \ldots , Y_{r-1}$
such that each
![]() $Y_s$
is of the form
$Y_s$
is of the form
![]() $x\mapsto x^{\ell +1}+\mu x^{2\ell +1}+ o(x^{\ell +s+1})$
. The construction is made by induction by letting
$x\mapsto x^{\ell +1}+\mu x^{2\ell +1}+ o(x^{\ell +s+1})$
. The construction is made by induction by letting
![]() $Y_{s+1}=h^* Y_s$
, with
$Y_{s+1}=h^* Y_s$
, with
![]() $h(x)=x+ax^{\ell +s+2}$
for some well-chosen a. Details are left to the reader.
$h(x)=x+ax^{\ell +s+2}$
for some well-chosen a. Details are left to the reader.
Proof Proof of Proposition 5.1.
Thanks to Lemma 5.3, we can start with a vector field X globally defined on
![]() $\mathbb {R}_+$
that has the form
$\mathbb {R}_+$
that has the form
We then define the function
![]() $\epsilon $
by the equality
$\epsilon $
by the equality
We want to prove that X is
![]() $C^{r}$
conjugate to
$C^{r}$
conjugate to
![]() $X_0 (x) := x^{\ell +1}+\mu x^{2\ell + 1}$
. For
$X_0 (x) := x^{\ell +1}+\mu x^{2\ell + 1}$
. For
![]() $y\in [0,1]$
, let
$y\in [0,1]$
, let
![]() $X_y (x) := X_0(x)+yx^{2\ell + 1}\epsilon (x)$
so that
$X_y (x) := X_0(x)+yx^{2\ell + 1}\epsilon (x)$
so that
![]() $X_1=X$
. Let Y be the horizontal
$X_1=X$
. Let Y be the horizontal
![]() $C^{\ell + r}$
vector field on
$C^{\ell + r}$
vector field on
![]() $S := \mathbb {R}_+\times [0,1]$
defined by
$S := \mathbb {R}_+\times [0,1]$
defined by
![]() $Y(x,y)=X_y(x) \, \partial _x + 0 \cdot \partial _y$
.
$Y(x,y)=X_y(x) \, \partial _x + 0 \cdot \partial _y$
.
We claim that it suffices to find a
![]() $C^{r}$
vector field Z on S of the form
$C^{r}$
vector field Z on S of the form
![]() $(x,y)\mapsto K(x,y) \, \partial _x + \partial _y$
, with K vanishing on
$(x,y)\mapsto K(x,y) \, \partial _x + \partial _y$
, with K vanishing on
![]() $\{0\}\times [0,1]$
and
$\{0\}\times [0,1]$
and
![]() $[Z,Y]=0$
near
$[Z,Y]=0$
near
![]() $\{0\}\times [0,1]$
. To show this, denote by
$\{0\}\times [0,1]$
. To show this, denote by
![]() $\phi _Z^t$
the flow of such a Z. Clearly,
$\phi _Z^t$
the flow of such a Z. Clearly,
![]() $\phi _Z^1 |_{|\mathbb {R}_+\times \{0\}}$
is of the form
$\phi _Z^1 |_{|\mathbb {R}_+\times \{0\}}$
is of the form
![]() $(x,0)\mapsto (\varphi (x),1)$
for some
$(x,0)\mapsto (\varphi (x),1)$
for some
![]() $C^{r}$
diffeomorphism
$C^{r}$
diffeomorphism
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {R}_+$
. We claim that
$\mathbb {R}_+$
. We claim that
![]() $\varphi _* X_0 = X_1$
. Indeed, the equality
$\varphi _* X_0 = X_1$
. Indeed, the equality
![]() $[Z,Y]=0$
implies that the flows of Z and Y commute near the ‘vertical’ segment
$[Z,Y]=0$
implies that the flows of Z and Y commute near the ‘vertical’ segment
![]() $\{0\}\times [0,1]$
. Let
$\{0\}\times [0,1]$
. Let
![]() $\mathcal {U}$
be a set of the form
$\mathcal {U}$
be a set of the form
![]() $\{\phi _Z^t(x,0): (x,t)\in [0,\eta ] \times [0,1]\}$
where these flows commute. Then, if
$\{\phi _Z^t(x,0): (x,t)\in [0,\eta ] \times [0,1]\}$
where these flows commute. Then, if
![]() $f_0^1$
and
$f_0^1$
and
![]() $f_1^1$
denote the time-
$f_1^1$
denote the time-
![]() $1$
maps of
$1$
maps of
![]() $X_0$
and
$X_0$
and
![]() $X_1$
, respectively, for every
$X_1$
, respectively, for every
![]() $x\in f_0^{-1}([0,\eta ])$
,
$x\in f_0^{-1}([0,\eta ])$
,
Therefore,
![]() $\varphi $
conjugates
$\varphi $
conjugates
![]() $f_0$
to
$f_0$
to
![]() $f_1$
, and thus
$f_1$
, and thus
![]() $X_0$
to
$X_0$
to
![]() $X_1$
(by the uniqueness of the vector fields associated to diffeomorphisms), as required.
$X_1$
(by the uniqueness of the vector fields associated to diffeomorphisms), as required.
We are thus reduced to proving the existence of a Z as above. Let us leave aside the questions of regularity for a while and assume that all involved functions are
![]() $C^\infty $
. In this case, according for example to [Reference Takens21, Proposition 2.3], the function
$C^\infty $
. In this case, according for example to [Reference Takens21, Proposition 2.3], the function
![]() $\epsilon $
can be assumed to be of the form
$\epsilon $
can be assumed to be of the form
![]() $x\mapsto x \, \delta (x)$
, with
$x\mapsto x \, \delta (x)$
, with
![]() $\delta $
smooth at
$\delta $
smooth at
![]() $0$
. We look for Z of the form
$0$
. We look for Z of the form
Let
![]() $F(x) := 1+\mu x^\ell $
so that
$F(x) := 1+\mu x^\ell $
so that
![]() $X_0(x)=x^{\ell + 1}F(x)$
. If
$X_0(x)=x^{\ell + 1}F(x)$
. If
![]() $(Y_x,Y_y)$
and
$(Y_x,Y_y)$
and
![]() $(Z_x,Z_y)$
denote the coordinates of Y and Z, respectively, then we have
$(Z_x,Z_y)$
denote the coordinates of Y and Z, respectively, then we have
![]() $[Z,Y] = \psi (x,y)\partial _x+0\cdot \partial _y$
, with
$[Z,Y] = \psi (x,y)\partial _x+0\cdot \partial _y$
, with
 $$ \begin{align*} \psi(x,y) =\ & \frac{\partial Y_x}{\partial x}Z_x - \frac{\partial Z_x}{\partial x}Y_x+\frac{\partial Y_x}{\partial y}Z_y \\ =\ & \left[(\ell+1)x^\ell F(x) + (2\ell + 1)x^{2\ell}y\epsilon (x)+yx^{2\ell +1} D\epsilon(x)\right]\times x^{\ell +1}H(x,y) \\ &\!\!\!\!\!\!\!\!\!\!\!- \left((\ell+1)x^{\ell}H(x,y)+x^{\ell +1}\frac{\partial H}{\partial x}(x,y)\right)\times\left(x^{\ell + 1}F(x)+x^{2\ell + 1}y\epsilon (x)\right) \, + \, x^{2\ell + 1}\epsilon (x)\\ =\ & x^{2\ell + 2}\left(\frac{\partial H}{\partial x}(x,y)(F(x)+x^\ell y\epsilon (x)) +H(x,y)y\left( \ell x^{\ell -1}\epsilon (x) + x^\ell D \epsilon(x)\right)+\delta(x)\right) \end{align*} $$
$$ \begin{align*} \psi(x,y) =\ & \frac{\partial Y_x}{\partial x}Z_x - \frac{\partial Z_x}{\partial x}Y_x+\frac{\partial Y_x}{\partial y}Z_y \\ =\ & \left[(\ell+1)x^\ell F(x) + (2\ell + 1)x^{2\ell}y\epsilon (x)+yx^{2\ell +1} D\epsilon(x)\right]\times x^{\ell +1}H(x,y) \\ &\!\!\!\!\!\!\!\!\!\!\!- \left((\ell+1)x^{\ell}H(x,y)+x^{\ell +1}\frac{\partial H}{\partial x}(x,y)\right)\times\left(x^{\ell + 1}F(x)+x^{2\ell + 1}y\epsilon (x)\right) \, + \, x^{2\ell + 1}\epsilon (x)\\ =\ & x^{2\ell + 2}\left(\frac{\partial H}{\partial x}(x,y)(F(x)+x^\ell y\epsilon (x)) +H(x,y)y\left( \ell x^{\ell -1}\epsilon (x) + x^\ell D \epsilon(x)\right)+\delta(x)\right) \end{align*} $$
(the terms involving
![]() $x^{2\ell +1}$
cancel). We hence need to solve an equation of the form
$x^{2\ell +1}$
cancel). We hence need to solve an equation of the form
with
This is a family of linear differential equations with variable x and parameter y, with a nonvanishing near
![]() $\{0\}\times [0,1]$
and a, b and
$\{0\}\times [0,1]$
and a, b and
![]() $\delta $
smooth (for now). The resolution of such equations ensures the existence of a smooth solution H (which is not unique, because of the choice of integration constants), which concludes the proof in the smooth case.
$\delta $
smooth (for now). The resolution of such equations ensures the existence of a smooth solution H (which is not unique, because of the choice of integration constants), which concludes the proof in the smooth case.
Let us now concentrate on our case, where
![]() $\ell \geq 1$
,
$\ell \geq 1$
,
![]() $r\ge \ell +1$
and X is only
$r\ge \ell +1$
and X is only
![]() $C^{\ell +r}$
(with
$C^{\ell +r}$
(with
![]() $(2\ell + 2)$
derivatives at
$(2\ell + 2)$
derivatives at
![]() $0$
if
$0$
if
![]() $r = \ell + 1$
). We want to check that, in this case, there exists H satisfying Equation (29) such that
$r = \ell + 1$
). We want to check that, in this case, there exists H satisfying Equation (29) such that
![]() $(x,y)\mapsto x^{\ell +1}H(x,y)$
is
$(x,y)\mapsto x^{\ell +1}H(x,y)$
is
![]() $C^{r}$
.
$C^{r}$
.
The existence of an H satisfying Equation (29) that is (smooth in y and)
![]() $C^1$
in x follows from that
$C^1$
in x follows from that
![]() $a,b$
and
$a,b$
and
![]() $\delta $
above are (smooth in y and) continuous in x, as we now check. Since we already know that
$\delta $
above are (smooth in y and) continuous in x, as we now check. Since we already know that
![]() $\epsilon $
is as regular as X away from
$\epsilon $
is as regular as X away from
![]() $0$
, that is,
$0$
, that is,
![]() $C^{\ell + r}$
, we are left with checking that
$C^{\ell + r}$
, we are left with checking that
![]() $x\mapsto x^\ell \epsilon (x)$
and
$x\mapsto x^\ell \epsilon (x)$
and
![]() $x\mapsto \frac {\epsilon (x)}x$
extend, respectively, to a
$x\mapsto \frac {\epsilon (x)}x$
extend, respectively, to a
![]() $C^1$
and a
$C^1$
and a
![]() $C^0$
function near
$C^0$
function near
![]() $0$
. The first point follows from Lemma 4.4 applied to
$0$
. The first point follows from Lemma 4.4 applied to
![]() $u(x):=x^{2\ell +1}\epsilon (x)$
,
$u(x):=x^{2\ell +1}\epsilon (x)$
,
![]() $k=\ell +r$
and
$k=\ell +r$
and
![]() $m=\ell $
(which actually shows that
$m=\ell $
(which actually shows that
![]() $x\mapsto x^\ell \epsilon (x)$
is
$x\mapsto x^\ell \epsilon (x)$
is
![]() $C^{r-1}$
with
$C^{r-1}$
with
![]() $r-1\ge \ell \ge 1$
). For the second point, if
$r-1\ge \ell \ge 1$
). For the second point, if
![]() $r\ge \ell +2$
, we know that
$r\ge \ell +2$
, we know that
and
![]() $\ell +r\ge 2\ell +2$
, hence by dividing each term by
$\ell +r\ge 2\ell +2$
, hence by dividing each term by
![]() $x^{2\ell + 1}$
we get
$x^{2\ell + 1}$
we get
![]() $\epsilon (x)=o(x)$
, so
$\epsilon (x)=o(x)$
, so
![]() $\delta $
indeed extends as a continuous function at
$\delta $
indeed extends as a continuous function at
![]() $0$
. If
$0$
. If
![]() $r=\ell +1$
, this is precisely where we use the additional assumption that X is
$r=\ell +1$
, this is precisely where we use the additional assumption that X is
![]() $(2\ell +2)$
times differentiable at
$(2\ell +2)$
times differentiable at
![]() $0$
, which by Lemma 5.3 implies that one can start with X of the form
$0$
, which by Lemma 5.3 implies that one can start with X of the form
hence
![]() $x^{2\ell +1}\epsilon (x)=o(x^{2\ell +2})$
and thus again
$x^{2\ell +1}\epsilon (x)=o(x^{2\ell +2})$
and thus again
![]() $\epsilon (x)=o(x)$
.
$\epsilon (x)=o(x)$
.
To conclude the proof, we finally need to show that
![]() $(x,y)\mapsto x^{\ell +1} H(x,y)$
is
$(x,y)\mapsto x^{\ell +1} H(x,y)$
is
![]() $C^r$
. To do this, we will actually prove by induction on
$C^r$
. To do this, we will actually prove by induction on
![]() $s \in [\![0,\ell + 1]\!]$
that
$s \in [\![0,\ell + 1]\!]$
that
![]() $H_s \!: (x,y)\mapsto x^sH(x,y)$
is
$H_s \!: (x,y)\mapsto x^sH(x,y)$
is
![]() $C^{r-\ell +s-1}$
.
$C^{r-\ell +s-1}$
.
Case
![]() $s=0$
. We have already given part of the ingredients for this initial case. If
$s=0$
. We have already given part of the ingredients for this initial case. If
![]() $r=\ell +1$
, then
$r=\ell +1$
, then
![]() $r-\ell +0-1=0$
, and we already know that
$r-\ell +0-1=0$
, and we already know that
![]() $H_0=H$
is continuous.
$H_0=H$
is continuous.
Now, consider
![]() $r\ge \ell +2$
. The theory of linear differential equations tells us that
$r\ge \ell +2$
. The theory of linear differential equations tells us that
![]() $H=H_0$
has one degree of differentiability more than the coefficients of the equation, so it suffices to check that these are
$H=H_0$
has one degree of differentiability more than the coefficients of the equation, so it suffices to check that these are
![]() $C^{r-\ell -2}$
. We have already seen that a and b in Equation (29) were respectively of class
$C^{r-\ell -2}$
. We have already seen that a and b in Equation (29) were respectively of class
![]() $C^{r-1}$
and
$C^{r-1}$
and
![]() $C^{r-2}$
, so a fortiori
$C^{r-2}$
, so a fortiori
![]() $C^{r-\ell -1}$
since
$C^{r-\ell -1}$
since
![]() $\ell \ge 1$
. Now, applying Lemma 4.4 to
$\ell \ge 1$
. Now, applying Lemma 4.4 to
![]() $u(x):=x^{2\ell +1}\epsilon (x)$
,
$u(x):=x^{2\ell +1}\epsilon (x)$
,
![]() $k=\ell +r$
and
$k=\ell +r$
and
![]() $m=2\ell $
, we get that
$m=2\ell $
, we get that
![]() $\epsilon $
is
$\epsilon $
is
![]() $C^{r-\ell -1}$
. Moreover, since
$C^{r-\ell -1}$
. Moreover, since
![]() $x^{2\ell + 1} \epsilon (x) = o(x^{\ell +r})$
, we have
$x^{2\ell + 1} \epsilon (x) = o(x^{\ell +r})$
, we have
![]() $\epsilon (x)=o(x^{r-\ell -1})$
, so
$\epsilon (x)=o(x^{r-\ell -1})$
, so
![]() $\epsilon $
is
$\epsilon $
is
![]() $(r-\ell -1)$
-flat. Applying Lemma 4.4 again but this time to
$(r-\ell -1)$
-flat. Applying Lemma 4.4 again but this time to
![]() $u:=\epsilon $
,
$u:=\epsilon $
,
![]() $k=r-\ell -1\ge 1$
and
$k=r-\ell -1\ge 1$
and
![]() $m=0$
, we get that
$m=0$
, we get that
![]() $\delta :x\mapsto \frac {\epsilon (x) }x$
is
$\delta :x\mapsto \frac {\epsilon (x) }x$
is
![]() $C^{r-\ell -2}$
, as required.
$C^{r-\ell -2}$
, as required.
Inductive step. Assume now that the induction hypothesis is true for some
![]() $0 \le s \le \ell $
. Then
$0 \le s \le \ell $
. Then
The first term of the right-hand side is
![]() $C^{r-\ell +s-1}$
by the induction hypothesis, and the second is equal to
$C^{r-\ell +s-1}$
by the induction hypothesis, and the second is equal to
 $$ \begin{align*}x^{s+1}\left(-\frac{b(x,y)}{a(x,y)}H(x,y) -\frac{c(x,y)}{a(x,y)}\right) = -\frac{x\cdot b(x,y)}{a(x,y)}H_s (x,y) -\frac{x^{s+1}c(x,y)}{a(x,y)}. \end{align*} $$
$$ \begin{align*}x^{s+1}\left(-\frac{b(x,y)}{a(x,y)}H(x,y) -\frac{c(x,y)}{a(x,y)}\right) = -\frac{x\cdot b(x,y)}{a(x,y)}H_s (x,y) -\frac{x^{s+1}c(x,y)}{a(x,y)}. \end{align*} $$
Since a is
![]() $C^{r-1}$
and thus
$C^{r-1}$
and thus
![]() $C^{r-\ell +s-1}$
, we are left with proving that the numerators of the fractions, namely
$C^{r-\ell +s-1}$
, we are left with proving that the numerators of the fractions, namely
are
![]() $C^{r-\ell +s-1}$
. For the second one, this follows from Lemma 4.4 still applied to
$C^{r-\ell +s-1}$
. For the second one, this follows from Lemma 4.4 still applied to
![]() $u(x):=x^{2\ell +1}\epsilon (x)$
and
$u(x):=x^{2\ell +1}\epsilon (x)$
and
![]() $k=\ell +r$
but this time with
$k=\ell +r$
but this time with
![]() $m=2\ell -s\le 2\ell <k$
. A last application with
$m=2\ell -s\le 2\ell <k$
. A last application with
![]() $m=r-2<k$
shows that
$m=r-2<k$
shows that
![]() $x\mapsto x^{\ell +1}\epsilon (x)$
is
$x\mapsto x^{\ell +1}\epsilon (x)$
is
![]() $C^{\ell +r-m-1}=C^{r+1}$
so that the first numerator is
$C^{\ell +r-m-1}=C^{r+1}$
so that the first numerator is
![]() $C^r$
and a fortiori
$C^r$
and a fortiori
![]() $C^{r-\ell +s-1}$
since
$C^{r-\ell +s-1}$
since
![]() $s\le \ell $
. This concludes the induction and thus the proof.
$s\le \ell $
. This concludes the induction and thus the proof.
Remark 5.4. Proposition 5.1 implies Takens’ normal form result: If X is a
![]() $C^{\infty }$
expanding vector field that is exactly
$C^{\infty }$
expanding vector field that is exactly
![]() $\ell $
-flat for some
$\ell $
-flat for some
![]() $\ell \geq 1$
, then X is
$\ell \geq 1$
, then X is
![]() $C^{\infty }$
conjugate to a vector field of the form
$C^{\infty }$
conjugate to a vector field of the form
![]() $x \mapsto x^{\ell +1} + \mu \, x^{2\ell +1}$
for a unique
$x \mapsto x^{\ell +1} + \mu \, x^{2\ell +1}$
for a unique
![]() $\mu $
. Indeed, we have shown the existence of such a
$\mu $
. Indeed, we have shown the existence of such a
![]() $C^r$
conjugacy
$C^r$
conjugacy
![]() $\varphi _r$
for each
$\varphi _r$
for each
![]() $r \geq \ell + 2$
. However, the conjugacy is unique up to composition with a member of the flow of X, which is a
$r \geq \ell + 2$
. However, the conjugacy is unique up to composition with a member of the flow of X, which is a
![]() $C^{\infty }$
diffeomorphism. Therefore,
$C^{\infty }$
diffeomorphism. Therefore,
![]() $\varphi _r$
and
$\varphi _r$
and
![]() $\varphi _{r+1}$
differ by the composition of a
$\varphi _{r+1}$
differ by the composition of a
![]() $C^{\infty }$
diffeomorphism, which easily implies that all the
$C^{\infty }$
diffeomorphism, which easily implies that all the
![]() $\varphi _r$
are actually
$\varphi _r$
are actually
![]() $C^{\infty }$
.
$C^{\infty }$
.
An analogous result holds for diffeomorphisms: Any two
![]() $C^{\infty }$
germs that are exactly
$C^{\infty }$
germs that are exactly
![]() $\ell $
-flat, both expanding or both contracting, and have the same iterative residue, are
$\ell $
-flat, both expanding or both contracting, and have the same iterative residue, are
![]() $C^{\infty }$
conjugate. Rather surprisingly, Takens’ proof of this fact passes through the famous Borel lemma on the realization of sequences of numbers as derivatives at the origin of
$C^{\infty }$
conjugate. Rather surprisingly, Takens’ proof of this fact passes through the famous Borel lemma on the realization of sequences of numbers as derivatives at the origin of
![]() $C^{\infty }$
germs, while our argument above avoids this.
$C^{\infty }$
germs, while our argument above avoids this.
6 Residues and distortion
Recall that an element g of a finitely-generated group is said to be distorted if
![]() $g^n$
may be written as a product of factors among the generators and their inverses whose total number grows sublinearly with respect to n. (This definition does not depend on the chosen generating system.) An element of a general group is a distortion element if it is distorted inside some finitely-generated subgroup. The next question is inspired from [Reference Navas14]:
$g^n$
may be written as a product of factors among the generators and their inverses whose total number grows sublinearly with respect to n. (This definition does not depend on the chosen generating system.) An element of a general group is a distortion element if it is distorted inside some finitely-generated subgroup. The next question is inspired from [Reference Navas14]:
Question 6.1. What are the distortion elements of the group
![]() $\mathrm {Diff}^{\omega }_+ (\mathbb {R},0)$
of germs of (orientation-preserving) real-analytic diffeomorphisms fixing the origin ?
$\mathrm {Diff}^{\omega }_+ (\mathbb {R},0)$
of germs of (orientation-preserving) real-analytic diffeomorphisms fixing the origin ?
An example of distortion element in the group of germs above is
Indeed, letting
![]() $h (x) = \frac {x}{2}$
, one has
$h (x) = \frac {x}{2}$
, one has
which easily yields
![]() $g^{2^m} = h^m g h^{-m}$
for all
$g^{2^m} = h^m g h^{-m}$
for all
![]() $m \geq 1$
. Using this, it is not hard to conclude that
$m \geq 1$
. Using this, it is not hard to conclude that
![]() $g^n$
may be written as a product of
$g^n$
may be written as a product of
![]() $O(\log (n))$
factors
$O(\log (n))$
factors
![]() $g^{\pm 1}, h^{\pm 1}$
. The case of the map below is particularly challenging.
$g^{\pm 1}, h^{\pm 1}$
. The case of the map below is particularly challenging.
Question 6.2. Is the germ
![]() $f(x) := x - x^2$
a distortion element of
$f(x) := x - x^2$
a distortion element of
![]() $\mathrm {Diff}^{\omega }_+ (\mathbb {R},0)$
?
$\mathrm {Diff}^{\omega }_+ (\mathbb {R},0)$
?
Observe that f is a distortion element of the much larger group
![]() $\mathrm {Diff}^1_+(\mathbb {R},0)$
. Indeed, by Theorem B, it is
$\mathrm {Diff}^1_+(\mathbb {R},0)$
. Indeed, by Theorem B, it is
![]() $C^1$
conjugated to g, which is a distortion element. Actually, this is a particular case of the much more general result below.
$C^1$
conjugated to g, which is a distortion element. Actually, this is a particular case of the much more general result below.
Proposition 6.3. Every (nontrivial) parabolic germ of real-analytic diffeomorphism of the line fixing the origin is a distortion element of the group
![]() $\mathrm {Diff}^1_+(\mathbb {R},0)$
.
$\mathrm {Diff}^1_+(\mathbb {R},0)$
.
Proof. Let f be such a germ and
![]() $\ell $
its order of contact with the identity. By Proposition 2.1, f is
$\ell $
its order of contact with the identity. By Proposition 2.1, f is
![]() $C^1$
conjugated to a germ g of the form
$C^1$
conjugated to a germ g of the form
 $$ \begin{align*}g(x) := \frac{x}{\sqrt[\ell]{1 \pm x^{\ell}}} = x \mp \frac{x^{\ell +1}}{\ell} + \ldots .\end{align*} $$
$$ \begin{align*}g(x) := \frac{x}{\sqrt[\ell]{1 \pm x^{\ell}}} = x \mp \frac{x^{\ell +1}}{\ell} + \ldots .\end{align*} $$
We are hence left to showing that g is a distortion element. But as above, this follows from the relation
![]() $h_\ell \, g \, h_\ell ^{-1} = g^2$
, where
$h_\ell \, g \, h_\ell ^{-1} = g^2$
, where
![]() $h_\ell (x) := \frac {x}{2^{{1/\ell }}}$
.
$h_\ell (x) := \frac {x}{2^{{1/\ell }}}$
.
We do not know whether the germ f above is a distortion element of the smaller group
![]() $\mathrm {Diff}^2_+(\mathbb {R},0)$
. A first difficulty of this question lies in that one cannot deduce distortion from a relation of type (30) because of the nonvanishing of the iterative residue of f, as proven below.
$\mathrm {Diff}^2_+(\mathbb {R},0)$
. A first difficulty of this question lies in that one cannot deduce distortion from a relation of type (30) because of the nonvanishing of the iterative residue of f, as proven below.
Proposition 6.4. Let g be a germ of
![]() $C^3$
diffeomorphism fixing the origin that is exactly
$C^3$
diffeomorphism fixing the origin that is exactly
![]() $1$
-tangent to the identity. If g is
$1$
-tangent to the identity. If g is
![]() $C^2$
conjugate to some element
$C^2$
conjugate to some element
![]() $g^t \in \mathrm {Diff}_+^3 (\mathbb {R},0)$
of its flow, with
$g^t \in \mathrm {Diff}_+^3 (\mathbb {R},0)$
of its flow, with
![]() $t \neq 1$
, then
$t \neq 1$
, then
![]() $\mathrm {Resit}(g)$
vanishes.
$\mathrm {Resit}(g)$
vanishes.
Proof. Since
![]() $\mathrm {Resit} (g)$
is invariant under
$\mathrm {Resit} (g)$
is invariant under
![]() $C^2$
conjugacy, by Equation (7) (see also Remark (3.1)), one has
$C^2$
conjugacy, by Equation (7) (see also Remark (3.1)), one has
 $$ \begin{align*}\mathrm{Resit} (g) = \mathrm{Resit} (g^t) = \frac{\mathrm{Resit}(g)}{|t|}.\end{align*} $$
$$ \begin{align*}\mathrm{Resit} (g) = \mathrm{Resit} (g^t) = \frac{\mathrm{Resit}(g)}{|t|}.\end{align*} $$
This easily implies
![]() $\mathrm {Resit} (g) = 0$
if
$\mathrm {Resit} (g) = 0$
if
![]() $t \neq 1$
. The case
$t \neq 1$
. The case
![]() $t = -1$
is impossible since a contracting diffeomorphisms cannot be conjugated to a expanding one.
$t = -1$
is impossible since a contracting diffeomorphisms cannot be conjugated to a expanding one.
To finish, let us mention that we do not even know whether the germ f above is a distortion element of the group
![]() $\widehat {\mathrm {Diff}} (\mathbb {R},0)$
of formal germs of diffeomorphisms. More generally, the next question seems challenging:
$\widehat {\mathrm {Diff}} (\mathbb {R},0)$
of formal germs of diffeomorphisms. More generally, the next question seems challenging:
Question 6.5. Given a field
![]() $\mathbb {K}$
, what are the distortion elements of
$\mathbb {K}$
, what are the distortion elements of
![]() $\widehat {\mathrm {Diff}}(\mathbb {K},0)$
? What about
$\widehat {\mathrm {Diff}}(\mathbb {K},0)$
? What about
![]() $\widehat {\mathrm {Diff}} (\mathbb {Z},0)$
?
$\widehat {\mathrm {Diff}} (\mathbb {Z},0)$
?
Acknowledgements
Hélène Eynard-Bontemps was funded by the IRGA project ADMIN of UGA and the CNRS in the context of a délégation. She would like to thank CMM (FB210005, BASAL funds for centers of excellence from ANID-Chile) / U. de Chile for the hospitality during this period and Michele Triestino for inspiring discussions related to this work. Andrés Navas was funded by Fondecyt Research Project 1220032 and would like to thank Adolfo Guillot, Jan Kiwi and Mario Ponce for useful discussions and insight concerning residues of parabolic germs in the complex setting. Both authors would like to thank the referee for her / his careful reading of the text and many remarks and corrections.
Competing interests
The authors have no competing interest to declare.