Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T06:18:07.108Z Has data issue: false hasContentIssue false
  • English
  • Français

ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  03 March 2021

Siegfried Böcherer  and
Soumya Das Open the ORCID record for Soumya Das [Opens in a new window]
Siegfried Böcherer
Affiliation:
Institut für Mathematik, Universität Mannheim, 68131 Mannheim, Germany ([email protected])
Soumya Das
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore – 560012, India ([email protected]) Alexander von Humboldt Fellow, Universität Mannheim, 68131 Mannheim, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that if F is a nonzero (possibly noncuspidal) vector-valued Siegel modular form of any degree, then it has infinitely many nonzero Fourier coefficients which are indexed by half-integral matrices having odd, square-free (and thus fundamental) discriminant. The proof uses an induction argument in the setting of vector-valued modular forms. Further, as an application of a variant of our result and complementing the work of A. Pollack, we show how to obtain an unconditional proof of the functional equation of the spinor L-function of a holomorphic cuspidal Siegel eigenform of degree 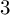$3$ and level 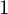$1$ .

Keywords

Fourier coefficientsSiegel modular formsfundamental discriminantvector-valuednonvanishing

MSC classification

Primary: 11F30: Fourier coefficients of automorphic forms
Secondary: 11F50: Jacobi forms
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 2001 - 2041
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, N. and Stegun, I., Handbook of Mathematical Functions (Dover, New York, 1965).Google Scholar
Ajouz, A., Hecke Operators on Jacobi Forms of Lattice Index and the Relation to Elliptic Modular Forms, Ph.D. thesis, University of Siegen, 2015, https://dspace.ub.uni-siegen.de/bitstream/ubsi/938/1/Dissertation_Ali_Ajouz.pdf.Google Scholar
Anamby, P. and Das, S., Distinguishing Hermitian cusp forms of degree $2$ by a certain subset of all Fourier coefficients, Publ. Mat. 63 (2019), 307–341.CrossRefGoogle Scholar
Andrianov, A. N., Euler products corresponding to Siegel modular forms of genus $2$ , Russian Math. Surveys 29(3) (1974), 45–116.CrossRefGoogle Scholar
Andrianov, A. N., Euler decompositions of theta-transformations of Siegel modular forms, Math. USSR-Sb. 34(1978), 291–341.CrossRefGoogle Scholar
Andrianov, A. N., The multiplicative arithmetic of Siegel modular forms, Russian Math. Surveys 34 (1979), 75–148.CrossRefGoogle Scholar
Asgari, M. and Schmidt, R., Siegel modular forms and representations, Manuscripta math. 104 (2001), 173–200.CrossRefGoogle Scholar
Balog, A. and Ono, K., The Chebotarev density theorem in short intervals and some questions of Serre, J. Number Theory, 91(2) (2001), 356–371.CrossRefGoogle Scholar
Böcherer, S., Über die Fourier-Jacobi-Entwicklung Siegelscher Eisensteinreihen, Math. Z. 183 (1983), 21–46.CrossRefGoogle Scholar
Böcherer, S. and Das, S., Petersson norms of not necessarily cuspidal Jacobi modular forms and applications, Adv. Math. 336 (2018), 336–375.CrossRefGoogle Scholar
Böcherer, S. and Das, S., On Fourier coefficients of elliptic modular forms $\text{mod}\ell$ with applications to Siegel modular forms, Manuscripta math. (to appear), https://arxiv.org/abs/2001.11700.Google Scholar
Borel, A., Linear Algebraic Groups, 2nd ed., Graduate Texts in Mathematics, 126 (Springer-Verlag, New York, 1991).CrossRefGoogle Scholar
Bykovskiĭ, V. A., A trace formula for the scalar product of Hecke series and its applications, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 226 (1996), 235–236.Google Scholar
Cassels, J. W. S., Rational Quadratic Forms (Academic Press, London-New York, 1978).Google Scholar
Courtieu, M. and Panchishkin, A., Non-Archimedean L-Functions and Arithmetical Modular Forms, Lecture Notes in Mathematics, 1471 (Springer, Berlin, 2004).Google Scholar
Delange, H., Généralisation du théorème de Ikehara, Ann. Sci. Éc. Norm. Supér. (9) 3(71) (1954), 213–242.CrossRefGoogle Scholar
Duke, W. and Iwaniec, H., Bilinear forms in the Fourier coefficients of half-integral weight cusp forms and sums over primes, Math. Ann. 286 (1990), 783–802.CrossRefGoogle Scholar
Eichler, M. and Zagier, D., The Theory of Jacobi Forms, Progress in Mathematics, 55 (Birkhäuser, Boston, 1985).CrossRefGoogle Scholar
Evdokimov, S. A., Dirichlet series, multiple Andrianov zeta-functions in the theory of Siegel modular forms of genus $3$ , Dokl. Akad. Nauk SSSR 277 (1984), 25–29.Google Scholar
Freitag, E., Siegelsche Modulfunktionen, Grundlehren der Mathematischen Wissenschaften, 254 (Springer-Verlag, Berlin, 1983).CrossRefGoogle Scholar
Freitag, E., Ein Verschwindungssatz für automorphe Formen zur Siegelschen Modulgruppe, Math. Z. 165 (1979), 11–18.CrossRefGoogle Scholar
Ibukiyama, T. and Kyomura, R., A generalization of vector-valued Jacobi forms, Osaka J. Math. 48 (2011), 783–808.Google Scholar
Iwaniec, H., Topics in Classical Automorphic Forms, Graduate Studies in Mathematics, 17 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Kitaoka, Y., Modular forms of degree $n$ and representations by quadratic forms, Nagoya Math. J. 74 (1979), 95–122.CrossRefGoogle Scholar
Kitaoka, Y., Arithmetic of Quadratic Forms, Cambridge Tracts in Mathematics, 106 (Cambridge University Press, Cambridge, UK, 1993).CrossRefGoogle Scholar
Klingen, H., Introductory Lectures on Siegel Modular Forms, Cambridge Studies in Advanced Mathematics, 20 (Cambridge University Press, Cambridge, UK, 1990).CrossRefGoogle Scholar
Lang, S., Introduction to Modular Forms, Grundlehren der Mathematischen Wissenschaften, 222 (Springer-Verlag, Berlin, 1995). Corrected reprint of the 1976 original, with appendixes by Zagier, D. and Feit, W..Google Scholar
Li, Y., Restriction of Coherent Hilbert Eisenstein series, Math. Ann. 368(1-2) (2017), 317–338.CrossRefGoogle Scholar
Miyake, T., Modular Forms, Springer Monographs in Mathematics, (Springer-Verlag, Berlin, 2006). Reprint of the first 1989 English edition, translated from the 1976 Japanese original by Maeda, Y..Google Scholar
Murty, M. Ram and Murty, V. Kumar, Non-Vanishing of $L$ -Functions and Applications, Progress in Mathematics, 157 (Birkhäuser Verlag, Basel, 1997).CrossRefGoogle Scholar
Pollack, A., The spin $L$ -function on $GS{p}_6$ for Siegel modular forms, Compos. Math. 153(7) (2017), 1391–1432.CrossRefGoogle Scholar
Rankin, R. A., Contributions to the theory of Ramanujan’s function $\tau (n)$ and similar arithmetic functions, II: Order of the Fourier coefficients of integral modular forms, Proc. Cambridge Philos. Soc. 35 (1939), 357–372.CrossRefGoogle Scholar
Saha, A., Siegel cusp forms of degree 2 are determined by their fundamental Fourier coefficients, Math. Ann. 355(1) (2013), 363–380.CrossRefGoogle Scholar
Selberg, A., On the estimation of Fourier coefficients of modular forms, Proc. Sympos. Pure Math. VIII (1965), 1–15.Google Scholar
Serre, J.-P., Quelques applications du théorème de densité de Chebotarev, Publ. Math. Inst. Hautes Études Sci. 54 (1981), 323–401.CrossRefGoogle Scholar
Serre, J.-P., Divisibilité de certaines fonctions arithmétiques, Séminaire Delange-Pisot-Poitou, Théor. Nombres 16(1) (1974-1975), 1–28.Google Scholar
Serre, J-P. and Stark, H., Modular forms of weight 1/2: Modular functions of one variable, VI, in Proceedings of the Second International Conference, University of Bonn, Bonn, 1976, pp. 27–67, Lecture Notes in Mathematics, 627, (Springer, Berlin, 1977).Google Scholar
Shahidi, F., On nonvanishing of $L$ -functions, Bull. Amer. Math. Soc. (N.S.) 2( 3) (1980), 462–464.CrossRefGoogle Scholar
Skoruppa, N.-P., Über den Zusammenhang zwischen Jacobiformen und Modulformen halbganzen Gewichts, Ph.D. thesis, Rheinische Friedrich-Wilhelms-Universität, Bonn, 1985.Google Scholar
Skoruppa, N.-P. and Zagier, D., Jacobi forms and a certain space of modular forms, Invent. Math. 94 (1988), 113–146.CrossRefGoogle Scholar
Stromberg, F., Weil representations associated with finite quadratic modules, Math. Z. 275 (2013), 509–527.CrossRefGoogle Scholar
Voight, J., Quaternion Algebras, https://math.dartmouth.edu/~jvoight/quat-book.pdf.Google Scholar
Weisinger, J., Some Results on Classical Eisenstein Series and Modular Forms over Function Fields, Ph.D. thesis, Harvard University, 1977.Google Scholar
Yamana, S., Determination of holomorphic modular forms by primitive Fourier coefficients, Math. Ann. 344 (2009), 853–863.CrossRefGoogle Scholar
Ziegler, C., Jacobi forms of higher degree, Abh. Math. Semin. Univ. Hambg. 59 (1989), 191–224.CrossRefGoogle Scholar