Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T16:27:56.515Z Has data issue: false hasContentIssue false
  • English
  • Français

ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS

Part of: Linear algebraic groups and related topics Lie groups Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  19 March 2021

Yongqi Feng ,
Eric Opdam  and
Maarten Solleveld Open the ORCID record for Maarten Solleveld [Opens in a new window]
Yongqi Feng
Affiliation:
Department of Mathematics, Shantou University, Daxue Road 243, 515063 Shantou, China ([email protected])
Eric Opdam
Affiliation:
Korteweg-de Vries Institute for Mathematics, Universiteit van Amsterdam, Science Park 105-107, 1098 XG Amsterdam, The Netherlands ([email protected])
Maarten Solleveld
Affiliation:
Institute for Mathematics, Astrophysics and Particle Physics, Radboud Universiteit, Heyendaalseweg 135, 6525AJ Nijmegen, The Netherlands ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

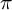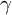Let G be a reductive p-adic group which splits over an unramified extension of the ground field. Hiraga, Ichino and Ikeda [24] conjectured that the formal degree of a square-integrable G-representation $\pi $ can be expressed in terms of the adjoint $\gamma $ -factor of the enhanced L-parameter of 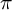$\pi $ . A similar conjecture was posed for the Plancherel densities of tempered irreducible G-representations.

We prove these conjectures for unipotent G-representations. We also derive explicit formulas for the involved adjoint 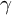$\gamma $ -factors.

Keywords

representation theoryp-adic groupsunipotent representationsformal degrees

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Secondary: 11S37: Langlands-Weil conjectures, nonabelian class field theory 20G25: Linear algebraic groups over local fields and their integers
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 1947 - 1999
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubert, A.-M., Moussaoui, A. and Solleveld, M., Graded Hecke algebras for disconnected reductive groups, in Geometric Aspects of the Trace Formula, Simons Symposia, pp. 23–84 (Springer, Cham, 2018).CrossRefGoogle Scholar
Aubert, A.-M., Moussaoui, A. and Solleveld, M., ‘Affine Hecke algebras for Langlands parameters’, Preprint, 2017, https://arxiv.org/abs/1701.03593.Google Scholar
Aubert, A.-M., Moussaoui, A. and Solleveld, M., Generalizations of the Springer correspondence and cuspidal Langlands parameters, Manuscripta Math. 157 (2018), 121–192.CrossRefGoogle Scholar
Borel, A., Automorphic L-functions, Proc. Symp. Pure Math. 33(2) (1979), 27–61.CrossRefGoogle Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local: II. Schémas en groupes. Existence d’une donnée radicielle valuée, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 5–184.CrossRefGoogle Scholar
Borel, A., Admissible representations of a semi-simple group over a local field with vectors fixed under an Iwahori subgroup, Invent. Math. 35 (1976) 233–259.CrossRefGoogle Scholar
Bushnell, J., Henniart, G. and Kutzko, P. C., Types and explicit Plancherel formulae for reductive $p$ -adic groups, in On Certain L-Functions, Clay Math. Proc., 13, pp. 55–80 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Bushnell, C. J. and Kutzko, P. C., Smooth representations of reductive $p$ -adic groups: structure theory via types, Proc. Lond. Math. Soc. (3) 77(3) (1998), 582–634.CrossRefGoogle Scholar
Carter, R. W., Simple Groups of Lie Type, Pure and Applied Mathematics, 28 (John Wiley & Sons, Location, 1972).Google Scholar
Carter, R. W., Finite Groups of Lie Type: Conjugacy Classes and Complex Characters, Pure and Applied Mathematics (John Wiley & Sons, London - New York - Sydney, 1985).Google Scholar
Casselman, W., ‘Introduction to the theory of admissible representations of $p$ -adic reductive groups’, Preprint, 1995, available at www.math.ubc.ca/∼cass/research/pdf/p-adic-book.pdf.Google Scholar
Ciubotaru, D. and Opdam, E. M., A uniform classification of discrete series representations of affine Hecke algebras, Algebra Number Theory 11(5) (2017), 1089–1134.CrossRefGoogle Scholar
DeBacker, S. and Reeder, M., Depth-zero supercuspidal $L$ -packets and their stability, Ann. of Math. (2) 169 (2009), 795–901.CrossRefGoogle Scholar
Dixmier, J., Les C*-algèbres et leurs representations, Cahiers Scientifiques, 29 (Gauthier-Villars Éditeur, Paris, 1969).Google Scholar
Feng, Y., A note on the spectral transfer morphisms for affine Hecke algebras, J. Lie Theory 29(4) (2019), 901–926.Google Scholar
Feng, Y. and Opdam, E., On a uniqueness property of cuspidal unipotent representations, Adv. Math. 375 (2020), https://doi.org/10.1016/j.aim.2020.107406.CrossRefGoogle Scholar
Feng, Y., Opdam, E. and Solleveld, M., Supercuspidal unipotent representations: L-packets and formal degrees, J. Éc. polytech. Math. 7 (2020), 1133–1193.CrossRefGoogle Scholar
Gan, W. T. and Gross, B. H., Haar measure and the Artin conductor, Trans. Amer. Math. Soc. 351(4) (1999), 1691–1704.Google Scholar
Gan, W.T. and Ichino, A., Formal degrees and local theta correspondence, Invent. Math. 195 (2014), 509–672.CrossRefGoogle Scholar
Geck, M. and Malle, G., ‘Reductive groups and the Steinberg map’, Preprint, 2016, https://arxiv.org/abs/1608.01156.Google Scholar
Gelbart, S. S. and Knapp, A. W., L-indistinguishability and R groups for the special linear group, Adv. Math. 43 (1982), 101–121.CrossRefGoogle Scholar
Gross, B. H., On the motive of a reductive group, Invent. Math. 130 (1997), 287–313.CrossRefGoogle Scholar
Gross, B. H. and Reeder, M., Arithmetic invariants of discrete Langlands parameters, Duke Math. J. 154(3) (2010), 431–508.CrossRefGoogle Scholar
Hiraga, K., Ichino, A. and Ikeda, T., Formal degrees and adjoint $\gamma$ -factors, J. Amer. Math. Soc. 21(1) (2008), 283–304; and correction, J. Amer. Math. Soc. 21(4) (2008), 1211–1213.CrossRefGoogle Scholar
Hiraga, K. and Saito, H., On L-packets for inner forms of $S{L}_n$ , Mem. Amer. Math. Soc. 215(1013) (2012).Google Scholar
Jacquet, H., Principal L-functions of the linear group, Proc. Symp. Pure Math. 33(2) (1979), 63–86.CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne-Langlands conjecture for Hecke algebras, Invent. Math. 87 (1987), 153–215.10.1007/BF01389157CrossRefGoogle Scholar
Langlands, R. P., On the classification of irreducible representations of real algebraic groups, in Representation Theory and Harmonic Analysis on Semisimple Lie Groups, Math. Surveys Monogr., 31, pp. 101–170 (American Mathematical Society, Providence, RI, 1989).CrossRefGoogle Scholar
Lusztig, G., Representations of Finite Chevalley Groups, Regional Conference Series in Mathematics, 39 (American Mathematical Society, Providence, RI, 1978).CrossRefGoogle Scholar
Lusztig, G., Classification of unipotent representations of simple $p$ -adic groups, Int. Math. Res. Not. IMRN 11 (1995), 517–589.10.1155/S1073792895000353CrossRefGoogle Scholar
Lusztig, G., Classification of unipotent representations of simple $p$ -adic groups II, Represent. Theory 6 (2002), 243–289.CrossRefGoogle Scholar
Macdonald, I. G., Spherical functions on a group of $p$ -adic type, University of Madras, 1971.Google Scholar
Morris, L., Tamely ramified intertwining algebras, Invent. Math. 114(1) (1993), 1–54.CrossRefGoogle Scholar
Morris, L., Level zero G-types, Compos. Math. 118(2) (1999), 135–157.CrossRefGoogle Scholar
Moy, A. and Prasad, G., Jacquet functors and unrefined minimal K-types, Comment. Math. Helv. 71 (1996), 98–121.CrossRefGoogle Scholar
Opdam, E. M., On the spectral decomposition of affine Hecke algebras, J. Inst. Math. Jussieu 3(4) (2004), 531–648.CrossRefGoogle Scholar
Opdam, E., Spectral correspondences for affine Hecke algebras, Adv. Math. 286 (2016), 912–957.CrossRefGoogle Scholar
Opdam, E. M., Spectral transfer morphisms for unipotent affine Hecke algebras, Selecta Math. (N.S.) 22(4) (2016), 2143–2207.CrossRefGoogle Scholar
Opdam, E. M., ‘Affine Hecke algebras and the conjectures of Hiraga, Ichino and Ikeda on the Plancherel density’, Conference in honor of Joseph Berstein, Proc. Sympos. Pure Math. 101, pp. 309–350, American Mathematical Society, 2019.Google Scholar
Opdam, E. M. and Solleveld, M., Discrete series characters for affine Hecke algebras and their formal dimensions, Acta Math. 205 (2010), 105–187.CrossRefGoogle Scholar
Pappas, G. and Rapoport, M., Twisted loop groups and their affine flag varieties, Adv. Math. 219(1) (2008), 118–198. With an appendix by T. Haines and M. Rapoport.CrossRefGoogle Scholar
Ram, A. and Rammage, J., Affine Hecke algebras, cyclotomic Hecke algebras and Clifford theory, in A Tribute to C.S. Seshadri (Chennai 2002), Trends in Mathematics, pp. 428–466 (Birkhäuser, Basel, 2003).CrossRefGoogle Scholar
Reeder, M., Formal degrees and L-packets of unipotent discrete series representations of exceptional $p$ -adic groups, J. Reine Angew. Math. 520 (2000), 37–93. With an appendix by F. Lübeck.Google Scholar
Reeder, M., Torsion automorphisms of simple Lie algebras, Enseign. Math. 56(2) (2010), 3–47.CrossRefGoogle Scholar
Satake, I., Theory of spherical functions on reductive algebraic groups over $p$ -adic fields, Publ. Math. Inst. Hautes Études Sci. 18 (1963), 5–69.CrossRefGoogle Scholar
Silberger, A. J., The Knapp-Stein dimension theorem for $p$ -adic groups, Proc. Amer. Math. Soc. 68(2) (1978), 243–246; and correction, Proc. Amer. Math. Soc. 76(1) (1979), 169–170.Google Scholar
Silberger, A. J., Isogeny restrictions of irreducible admissible representations are finite direct sums of irreducible admissible representations, Proc. Amer. Math. Soc. 73(2) (1979), 263–264.CrossRefGoogle Scholar
Solleveld, M., On the classification of irreducible representations of affine Hecke algebras with unequal parameters, Represent. Theory 16 (2012), 1–87.CrossRefGoogle Scholar
Solleveld, M., On completions of Hecke algebras, in Representations of Reductive p-adic Groups, Progress in Mathematics, 328, pp. 207–262 (Birkhäuser, Singapore, 2019).CrossRefGoogle Scholar
Solleveld, M., ‘A local Langlands correspondence for unipotent representations’, Preprint, 2018, https://arxiv.org/abs/1806.11357.Google Scholar
Solleveld, M., Langlands parameters, functoriality and Hecke algebras, Pacific J. Math. 304(1) (2020), 209–302.CrossRefGoogle Scholar
Solleveld, M., ‘On unipotent representations of ramified $p$ -adic groups’, Preprint, 2019, https://arxiv.org/abs/1912.08451.Google Scholar
Springer, T. A., Linear Algebraic Groups, 2nd ed., Progress in Mathematics, 9 (Birkhäuser, Boston, 1998).CrossRefGoogle Scholar
Tadić, M., Notes on representations of non-archimedean $\mathrm{SL}(n)$ , Pacific J. Math. 152(2) (1992), 375–396.CrossRefGoogle Scholar
Tate, J., Number theoretic background, Proc. Symp. Pure Math. 33(2) (1979), 3–26.CrossRefGoogle Scholar
Tits, J., Reductive groups over local fields, in Automorphic Forms, Representations and L-Functions Part I, Proc. Sympos. Pure Math., 33, pp. 29–69 (American Mathematical Society, Providence, RI, 1979)CrossRefGoogle Scholar
Waldspurger, J.-L., La formule de Plancherel pour les groupes p-adiques (d’après Harish-Chandra), J. Inst. Math. Jussieu 2(2) (2003), 235–333.CrossRefGoogle Scholar