Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T03:38:08.106Z Has data issue: false hasContentIssue false
  • English
  • Français

NON-UNITARISABLE REPRESENTATIONS AND MAXIMAL SYMMETRY

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  01 July 2015

Valentin Ferenczi  and
Christian Rosendal
Valentin Ferenczi
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, rua do Matão 1010, Cidade Universitária, 05508-90 São Paulo, SP, Brazil Equipe d’Analyse Fonctionnelle, Institut de Mathématiques de Jussieu, Université Pierre et Marie Curie - Paris 6, Case 247, 4 place Jussieu, 75252 Paris Cedex 05, France ([email protected])
Christian Rosendal
Affiliation:
Department of Mathematics, Statistics, and Computer Science (M/C 249), University of Illinois at Chicago, 851 S. Morgan St., Chicago, IL 60607-7045, USA ([email protected]) URL: http://homepages.math.uic.edu/∼rosendal
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate questions of maximal symmetry in Banach spaces and the structure of certain bounded non-unitarisable groups on Hilbert space. In particular, we provide structural information about bounded groups with an essentially unique invariant complemented subspace. This is subsequently combined with rigidity results for the unitary representation of 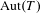$\text{Aut}(T)$ on 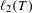$\ell _{2}(T)$, where $T$ is the countably infinite regular tree, to describe the possible bounded subgroups of 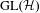$\text{GL}({\mathcal{H}})$ extending a well-known non-unitarisable representation of 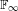$\mathbb{F}_{\infty }$.

As a related result, we also show that a transitive norm on a separable Banach space must be strictly convex.

Keywords

unitarisable representationsmaximal norms

MSC classification

Primary: 46B03: Isomorphic theory (including renorming) of Banach spaces 46B04: Isometric theory of Banach spaces
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 2 , April 2017 , pp. 421 - 445
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banach, S., Théorie des opérations linéaires. (French) [Theory of linear operators] (Éditions Jacques Gabay, Sceaux, 1993). Reprint of the 1932 original.Google Scholar
Becerra Guerrero, J. and Rodríguez-Palacios, A., Transitivity of the norm on Banach spaces, Extracta Math. 17(1) (2002), 1–58.Google Scholar
Benyamini, Y. and Lindenstrauss, J., Geometric Nonlinear Functional Analysis vol. 1, American Mathematical Society Colloquium Publications, Volume 48 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Bourgain, J., Translation invariant forms on L p (G), (1 < p < ∞), Ann. Inst. Fourier (Grenoble) 36(1) (1986), 97–104.CrossRefGoogle Scholar
Cabello-Sánchez, F., Regards sur le problème des rotations de Mazur, Extracta Math. 12 (1997), 97–116.Google Scholar
Cabello-Sánchez, F., Maximal symmetric norms on Banach spaces, Math. Proc. R. Ir. Acad. 98A(2) (1998), 121–130.Google Scholar
Day, M., Means for the bounded functions and ergodicity of the bounded representations of semi-groups, Trans. Amer. Math. Soc. 69 (1950), 276–291.Google Scholar
Deville, R., Godefroy, G. and Zizler, V., Smoothness and renormings in Banach spaces, in Pitman Monographs and Surveys in Pure and Applied Mathematics vol. 64 (Longman Scientific & Technical, Harlow, 1993). Copublished in the United States with John Wiley & Sons, Inc., New York.Google Scholar
Dilworth, S. J. and Randrianantoanina, B., On an isomorphic Banach–Mazur rotation problem and maximal norms in Banach spaces, J. Funct. Anal. 268(6) (2015), 1587–1611.Google Scholar
Dixmier, J., Les moyennes invariantes dans les semi-groupes et leurs applications, Acta Sci. Math. (Szeged) 12 (1950), 213–227.Google Scholar
Ehrenpreis, L. and Mautner, F. I., Uniformly bounded representations of groups, Proc. Natl. Acad. Sci. USA 41 (1955), 231–233.Google Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos, V. and Zizler, V., Banach space theory. The basis for linear and nonlinear analysis, in CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC (Springer, New York, 2011).Google Scholar
Ferenczi, V. and Rosendal, C., On isometry groups and maximal symmetry, Duke Math. J. 162(10) (2013), 1771–1831.CrossRefGoogle Scholar
Finet, C., Uniform convexity properties of norms on a superreflexive Banach space, Israel J. Math. 53 (1986), 81–92.Google Scholar
Kalton, N. J. and Wood, G. V., Orthonormal systems in Banach spaces and their applications, Math. Proc. Cambridge Philos. Soc. 79 (1976), 493–510.Google Scholar
Lancien, G., Dentability indices and locally uniformly convex renormings, Rocky Mountain J. Math. 23(2) (1993), 635–647.CrossRefGoogle Scholar
Lusky, W., The Gurarij spaces are unique, Arch. Math. 27(6) (1976), 627–635.Google Scholar
Lusky, W., A note on rotations in separable Banach spaces, Studia Math. 65 (1979), 239–242.CrossRefGoogle Scholar
Mazur, S., Quelques propriétés caractéristiques des espaces euclidiens, C. R. Acad. Sci. Paris 207 (1938), 761–764.Google Scholar
Ozawa, N., An invitation to the similarity problems (after Pisier), Surikaisekikenkyusho Kokyuroku 1486 (2006), 27–40.Google Scholar
Pełczyński, A. and Rolewicz, S., Best norms with respect to isometry groups in normed linear spaces, Short communication on International Mathematical Congress in Stockholm (1964), 104.Google Scholar
Pisier, G., Similarity Problems and Completely Bounded Maps. Second, Expanded Edition. Includes the Solution to ‘The Halmos Problem’, Lecture Notes in Mathematics, Volume 1618 (Springer, Berlin, 2001).Google Scholar
Pytlic, T. and Szwarc, R., An analytic family of uniformly bounded representations of free groups, Acta Math. 157(3–4) (1986), 287–309.CrossRefGoogle Scholar
Rolewicz, S., On convex sets containing only points of support, Comment. Math. (1978), 279–281. Special issue dedicated to Władysław Orlicz on the occasion of his seventy-fifth birthday. Special Issue 1.Google Scholar
Rolewicz, S., Metric Linear Spaces, 2nd ed. (Polish Scientific Publishers, Warszawa, 1984).Google Scholar