Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T14:19:37.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Noncommutative motives of Azumaya algebras

Part of: Categories with structure Algebraic geometry: Foundations Higher algebraic $K$-theory $K$-theory in geometry (Co)homology theory

Published online by Cambridge University Press:  10 March 2014

Gonçalo Tabuada  and
Michel Van den Bergh
Gonçalo Tabuada
Affiliation:
Department of Mathematics, MIT, Cambridge, MA 02139, USA Departamento de Matemática e CMA, FCT-UNL, Quinta da Torre, 2829-516 Caparica, Portugal ([email protected]) http://math.mit.edu/∼tabuada
Michel Van den Bergh
Affiliation:
Departement WNI, Universiteit Hasselt, 3590 Diepenbeek, Belgium ([email protected]) http://hardy.uhasselt.be/personal/vdbergh/Members/∼michelid.html
Get access Rights & Permissions [Opens in a new window]

Abstract

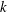Let $k$ be a base commutative ring, 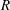$R$ a commutative ring of coefficients, 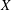$X$ a quasi-compact quasi-separated 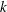$k$-scheme, and 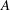$A$ a sheaf of Azumaya algebras over 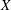$X$ of rank $r$. Under the assumption that 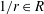$1/r\in R$, we prove that the noncommutative motives with 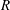$R$-coefficients of 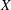$X$ and $A$ are isomorphic. As an application, we conclude that a similar isomorphism holds for every 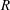$R$-linear additive invariant. This leads to several computations. Along the way we show that, in the case of finite-dimensional algebras of finite global dimension, all additive invariants are nilinvariant.

Keywords

algebraic K-theoryAzumaya algebrascyclic homologynilinvariancenoncommutative algebraic geometrynoncommutative motives

MSC classification

Primary: 14A22: Noncommutative algebraic geometry 14F05: Sheaves, derived categories of sheaves and related constructions 16H05: Separable algebras (e.g., quaternion algebras, Azumaya algebras, etc.) 18D20: Enriched categories (over closed or monoidal categories) 19D55: $K$-theory and homology; cyclic homology and cohomology 19E08: $K$-theory of schemes
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 2 , April 2015 , pp. 379 - 403
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antieau, B., Letter to the authors, July 31, 2013.Google Scholar
Auslander, M. and Goldman, O., The Brauer group of a commutative ring, Trans. Am. Math. Soc. 97 (1960), 367–409.Google Scholar
Azumaya, Goro., On maximally central algebras, Nagoya Math. J. 2 (1951), 119–150.CrossRefGoogle Scholar
Bernardara, M., A semiorthogonal decomposition for Brauer Severi schemes, Math. Nachr. 282(10) (2009), 1406–1413.CrossRefGoogle Scholar
Bernardara, M. and Tabuada, G., Relations between the Chow motive and the noncommutative motive of a smooth projective variety. Available at arXiv:arXiv:1303.3172.Google Scholar
Bernardara, M. and Tabuada, G., From semi-orthogonal decompositions to polarized intermediate Jacobians via Jacobians of noncommutative motives. Available at arXiv:arXiv:1305.4687.Google Scholar
Bezrukavnikov, R., Mirković, I. and Rumynin, D., Localization of modules for a semisimple Lie algebra in prime characteristic, Ann. Maths 167 (2008), 945–991.Google Scholar
Blumberg, A. and Mandell, M., Localization theorems in topological Hochschild homology and topological cyclic homology, Geom. Topol. 16 (2012), 1053–1120.Google Scholar
Bondal, A. and Orlov, D., Semiorthogonal decomposition for algebraic varieties. Available at arXiv:arXiv:alg-geom/9506012.Google Scholar
Bondal, A. and Van den Bergh, M., Generators and representability of functors in commutative and noncommutative geometry, Mosc. Math. J. 3(1) (2003), 1–36.Google Scholar
Buchweitz, R., Green, E., Madsen, D. and Solberg, Ø., Finite Hochschild cohomology without finite global dimension, Math. Res. Lett. 12(5–6) (2005), 805–816.CrossRefGoogle Scholar
Cisinski, D.-C. and Tabuada, G., Symmetric monoidal structure on noncommutative motives, J. K-Theory 9(2) (2012), 201–268.CrossRefGoogle Scholar
Cortiñas, G. and Weibel, C., Homology of Azumaya algebras, Proc. Am. Math. Soc. 121(1) (1994), 53–55.Google Scholar
Fulton, W. and Lang, S., Riemann–Roch Algebra, Grundlehren der Mathematischen Wissenschaften, Volume 277 (Springer-Verlag, New York, 1985).CrossRefGoogle Scholar
Gabber, O., Some theorems on Azumaya algebras, in The Brauer Group, Lecture Notes in Math., Volume 844, pp. 129–209 (Springer, Berlin, New York, 1981).Google Scholar
Gille, P. and Szamuely, T., Central Simple Algebras and Galois Cohomology, Cambridge Studies in Advanced Mathematics, Volume 101 (Cambridge University Press, Cambridge, 2006).Google Scholar
Grothendieck, A., Le groupe de Brauer I: Algèbres d’Azumaya et interprétations diverses, in Dix Exposés sur la Cohomologie des Schémas, pp. 46–66 (North-Holland, Amsterdam, Masson, Paris, 1968).Google Scholar
Hazrat, R. and Hoobler, R. T., K-theory of Azumaya algebras over schemes, Comm. Algebra 41(4) (2013), 1268–1277.Google Scholar
Keller, B., On differential graded categories, in International Congress of Mathematicians (Madrid), Vol. II, pp. 151–190 (Eur. Math. Soc., Zürich, 2006).Google Scholar
Keller, B., On the cyclic homology of exact categories, J. Pure Appl. Algebra 136(1) (1999), 1–56.Google Scholar
Keller, B., On the cyclic homology of ringed spaces and schemes, Doc. Math. 3 (1998), 231–259.Google Scholar
Keller, B., Invariance and localization for cyclic homology of dg algebras, J. Pure Appl. Algebra 123(1–3) (1998), 223–273.Google Scholar
Kontsevich, M., Noncommutative motives. Talk at the Institute for Advanced Study on the occasion of the $61^{\text{st}}$ birthday of Pierre Deligne, October 2005. Video available at http://video.ias.edu/Geometry-and-Arithmetic.Google Scholar
Kontsevich, M., Triangulated categories and geometry. Course at the École Normale Supérieure, Paris, 1998. Notes available at www.math.uchicago.edu/mitya/langlands.html.Google Scholar
Kontsevich, M., Mixed noncommutative motives. Talk at the Workshop on Homological Mirror Symmetry, Miami, 2010. Notes available at www-math.mit.edu/auroux/frg/miami10-notes.Google Scholar
Kontsevich, M., Notes on motives in finite characteristic, in Algebra, Arithmetic, and Geometry: In Honor of Yu. I. Manin. Vol. II, Progr. Math., Volume 270, pp. 213–247 (Birkhäuser, Boston, MA, 2009).Google Scholar
Kontsevich, M., Deformation quantization of algebraic varieties, Lett. Math. Phys. 56(3) (2001), 271–294 EuroConférence Moshé Flato 2000, Part III (Dijon).Google Scholar
Knus, M.-A. and Ojanguren, M., Théorie de la Descente et Algèbres D’Azumaya, Lecture Notes in Mathematics, Volume 389 (Springer-Verlag, Berlin, New York, 1974).CrossRefGoogle Scholar
Kuznetsov, A., Derived categories of cubic fourfolds, in Cohomological and Geometric Approaches to Rationality Problems. New Perspectives, (ed. Fedor, Bogomolov and Yuri, Tschinkel), Series: Progress in Mathematics, Volume 282 (Birkhauser, 2010).Google Scholar
Kuznetsov, A., Derived categories of quadric fibrations and intersections of quadrics, Adv. Maths 218(5) (2008), 1340–1369.Google Scholar
Lam, T. Y., Introduction to Quadratic Forms Over Fields, Graduate Studies in Mathematics, Volume 67 (American Mathematical Society, 2005).Google Scholar
Lunts, V. and Orlov, D., Uniqueness of enhancement for triangulated categories, J. Amer. Math. Soc. 23 (2010), 853–908.Google Scholar
Marcolli, M. and Tabuada, G., From exceptional collections to motivic decompositions via noncommutative motives, J. Reine Angew. Math. (2014), Available at arXiv:arXiv:1202.6297 (in press).Google Scholar
Quillen, D., Higher algebraic K-theory: I, in Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), Lecture Notes in Math., Volume 341, pp. 85–147 (Springer, Berlin, 1973).Google Scholar
Revoy, P., Algèbres de Weyl en caractéristique p , C. R. Acad. Sci. Paris. Sér. A-B 276 (1973), 225–228 A.Google Scholar
Schlichting, M., Negative K-theory of derived categories, Math. Z. 253(1) (2006), 97–134.Google Scholar
Tabuada, G., A guided tour through the garden of noncommutative motives, Clay Math. Proc. 16 (2012), 259–276.Google Scholar
Tabuada, G., Generalized spectral categories, topological Hochschild homology, and trace maps, Algebr. Geom. Topol. 10 (2010), 137–213.Google Scholar
Tabuada, G., Higher K-theory via universal invariants, Duke Math. J. 145(1) (2008), 121–206.Google Scholar
Tabuada, G., Invariants additifs de dg-catégories, Int. Math. Res. Not. 53 (2005), 3309–3339.Google Scholar
Thomason, R. W., The classification of triangulated subcategories, Compos. Math. 105(1) (1997), 1–27.Google Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories, in Grothendieck Festschrift, Volume III, Progress in Math., Volume 88, pp. 247–436 (Birkhäuser, Boston, Bassel, Berlin, 1990).Google Scholar
Waldhausen, F., Algebraic K-theory of spaces, in Algebraic and Geometric Topology (New Brunswick, N. J., 1983), Lecture Notes in Math., Volume 1126, pp. 318–419 (Springer, Berlin, 1985).Google Scholar
Weibel, C., The K-book: An Introduction to Algebraic K-Theory, Graduate Studies in Math., Volume 145 (AMS, 2013).Google Scholar