Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T17:58:37.420Z Has data issue: false hasContentIssue false
  • English
  • Français

NEXT ORDER ASYMPTOTICS AND RENORMALIZED ENERGY FOR RIESZ INTERACTIONS

Part of: Special matrices Equilibrium statistical mechanics

Published online by Cambridge University Press:  29 May 2015

Mircea Petrache  and
Sylvia Serfaty
Mircea Petrache
Affiliation:
UPMC Univ. Paris 6, UMR 7598 Laboratoire Jacques-Louis Lions, Paris, F-75005, France ([email protected])
Sylvia Serfaty
Affiliation:
UPMC Univ. Paris 6, UMR 7598 Laboratoire Jacques-Louis Lions, Paris, F-75005, France ([email protected]) Courant Institute, New York University, 251 Mercer st, New York, NY 10012, USA ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study systems of $n$ points in the Euclidean space of dimension 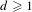$d\geqslant 1$ interacting via a Riesz kernel 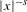$|x|^{-s}$ and confined by an external potential, in the regime where 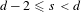$d-2\leqslant s<d$. We also treat the case of logarithmic interactions in dimensions 1 and 2. Our study includes and retrieves all cases previously studied in Sandier and Serfaty [2D Coulomb gases and the renormalized energy, Ann. Probab. (to appear); 1D log gases and the renormalized energy: crystallization at vanishing temperature (2013)] and Rougerie and Serfaty [Higher dimensional Coulomb gases and renormalized energy functionals, Comm. Pure Appl. Math. (to appear)]. Our approach is based on the Caffarelli–Silvestre extension formula, which allows one to view the Riesz kernel as the kernel of an (inhomogeneous) local operator in the extended space 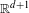$\mathbb{R}^{d+1}$.

As 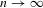$n\rightarrow \infty$, we exhibit a next to leading order term in 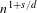$n^{1+s/d}$ in the asymptotic expansion of the total energy of the system, where the constant term in factor of 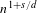$n^{1+s/d}$ depends on the microscopic arrangement of the points and is expressed in terms of a ‘renormalized energy’. This new object is expected to penalize the disorder of an infinite set of points in whole space, and to be minimized by Bravais lattice (or crystalline) configurations. We give applications to the statistical mechanics in the case where temperature is added to the system, and identify an expected ‘crystallization regime’. We also obtain a result of separation of the points for minimizers of the energy.

Keywords

Riesz energyrenormalized energyFekete pointspoint separation

MSC classification

Primary: 82B05: Classical equilibrium statistical mechanics (general) 82B21: Continuum models (systems of particles, etc.) 82B26: Phase transitions (general) 15B52: Random matrices
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 3 , June 2017 , pp. 501 - 569
Copyright
© Cambridge University Press 2015 

References

Alberti, G. and Müller, S., A new approach to variational problems with multiple scales, Comm. Pure Appl. Math. 54(7) (2001), 761–825.CrossRefGoogle Scholar
Avila, A., Last, Y. and Simon, B., Bulk universality and clock spacing of zeros for ergodic Jacobi matrices with absolutely continuous spectrum, Anal. PDE 3(1) (2010), 81–108.CrossRefGoogle Scholar
Bateman, P. T. and Grosswald, E., On Epstein’s zeta function, Acta Arith. 9(4) (1964), 365–373.CrossRefGoogle Scholar
Becker, M. E., Multiparameter groups of measure-preserving transformations: a simple proof of Wiener’s ergodic theorem, Ann. Prob. 9(3) (1981), 504–509.CrossRefGoogle Scholar
Bétermin, L., Renormalized energy and asymptotic expansion of optimal logarithmic energy on the sphere, arXiv:1404.4485.Google Scholar
Bethuel, F., Brezis, H. and Hélein, F., Ginzburg–Landau Vortices, Progress in Nonlinear Partial Differential Equations and Their Applications (Birkhäuser, 1994).CrossRefGoogle Scholar
Borodachov, S., Hardin, D. H. and Saff, E. B., Minimal discrete energy on the sphere and other manifolds (forthcoming).Google Scholar
Borodin, A. and Serfaty, S., Renormalized energy concentration in random matrices, Comm. Math. Phys. 320(1) (2013), 199–244.CrossRefGoogle Scholar
Brascamp, H. J. and Lieb, E. H., Some inequalities for Gaussian measures and the long-range order of the one-dimensional plasma, in Functional Integration and its Applications(ed. Arthurs, A. M.), (Clarendon Press, 1975).Google Scholar
Brauchart, J. S., Dragnev, P. D. and Saff, E. B., Riesz extremal measures on the sphere for axis-supported external fields, J. Math. Anal. Appl. 356(2) (2009), 769–792.CrossRefGoogle Scholar
Brauchart, J. S., Dragnev, P. D. and Saff, E. B., Riesz external field problems on the hypersphere and optimal point separation, Potential Anal. (to appear).Google Scholar
Brauchart, J. S., Hardin, D. P. and Saff, E. B., The next order term for optimal Riesz and logarithmic energy asymptotics on the sphere, in Recent Advances in Orthogonal Polynomials, Special Functions, and their Applications, Contemporary Mathematics, Volume 578, pp. 31–61 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Caffarelli, L. A. and Silvestre, L., An extension problem related to the fractional Laplacian, Comm. Partial Differential Equations 32(7–9) (2007), 1245–1260.CrossRefGoogle Scholar
Caffarelli, L. A., Salsa, S. and Silvestre, L., Regularity estimates for the solution and the free boundary of the obstacle problem of the fractional Laplacian, Invent. Math. 171(2) (2008), 425–461.CrossRefGoogle Scholar
Caffarelli, L. A., Roquejoffre, J.-M. and Sire, Y., Variational problems for free boundaries for the fractional Laplacian, J. Eur. Math. Soc. (JEMS) 12(5) (2010), 1151–1179.CrossRefGoogle Scholar
Cassels, J. W. S., On a problem of Rankin about the Epstein zeta-function, Proc. Glasg. Math. Assoc. 4 (1959), 73–80.CrossRefGoogle Scholar
Chan, T. H., Finding almost squares, Acta Arith. 121 (2006), 221–232.CrossRefGoogle Scholar
Chatard, J., Applications des propriétés de moyenne d’un groupe localement compact à la théorie ergodique, Ann. I. H. P. (B) Probab. Stat. 6(4) (1970), 307–326.Google Scholar
Chafaï, D., Gozlan, N. and Zitt, P.-A., First order global asymptotics for confined particles with singular pair repulsion, Ann. Appl. Probab. 24(6) (2014), 2371–2413.CrossRefGoogle Scholar
Choquet, G., Diamètre transfini et comparaison de diverses capacités, Technical report, Faculté des Sciences de Paris (1958).Google Scholar
Chowla, S. and Selberg, A., On Epstein’s zeta-function, J. Reine Angew. Math. 227 (1967), 86–110.Google Scholar
Cohn, H. and Elkies, N., New upper bounds on sphere packings. I, Ann. of Math. (2) 157(2) (2004), 689–714.CrossRefGoogle Scholar
Cohn, H. and Kumar, A., Universally optimal distribution of points on spheres, J. Amer. Math. Soc. 20(1) (2007), 99–148 (electronic).CrossRefGoogle Scholar
Diananda, P. H., Notes on two lemmas concerning the Epstein zeta-function, Proc. Glasg. Math. Assoc. 6 (1964), 202–204.CrossRefGoogle Scholar
Ennola, V., A lemma about the Epstein zeta-function, Proc. Glasg. Math. Assoc. 6 (1964), 198–201.CrossRefGoogle Scholar
Ennola, V., On a problem about the Epstein zeta function, Proc. Cambridge Philos. Soc. 60 (1964), 855–875.CrossRefGoogle Scholar
Fabes, E. B., Kenig, C. E. and Serapioni, R. P., The local regularity of solutions of degenerate elliptic equations, Comm. Partial Differential Equations 7(1) (1982), 77–116.CrossRefGoogle Scholar
Flatley, L. and Theil, F., Face-centered cubic crystallization of atomistic configurations, Arch. Rational. Mech. Anal. (2015), doi:10.1007/s00205-015-0862-1.CrossRefGoogle Scholar
Forrester, P. J., London Mathematical Society Monographs Series, Volume 34 (Princeton University Press, 2010).Google Scholar
Frostman, O., Potentiel d’équilibre et capacité des ensembles avec quelques applications à la théorie des fonctions, Meddelanden Mat. Sem. Univ. Lund 3 115 s (1935).Google Scholar
Hardin, D. H., Saff, E. B., Simanek, B. Z. and Su, Y., Second order asymptotics for long-range Riesz potentials on flat torii (in preparation).Google Scholar
Hörmander, L., The Analysis of Linear Partial Differential Operators, I: Distribution Theory and Fourier Analysis (Springer, 1983).Google Scholar
Landkof, N. S., Foundations of Modern Potential Theory (Springer, 1972).CrossRefGoogle Scholar
Leblé, T., A uniqueness result for minimizers of the 1D log-gas renormalized energy, J. Funct. Anal. (to appear), arXiv:1408.2283.Google Scholar
Lenard, A., Exact statistical mechanics of a one-dimensional system with Coulomb forces, J. Math. Phys. 2 (1961), 682–693.CrossRefGoogle Scholar
Lenard, A., Exact statistical mechanics of a one-dimensional system with Coulomb forces III: statistics of the electric field, J. Math. Phys. 4 (1963), 533–543.CrossRefGoogle Scholar
Lieb, E., Personal communication.Google Scholar
Molchanov, S. A. and Ostrovski, E., Symmetric stable processes as traces of degenerate diffusion processes, Theory Probab. Appl. 14 (1969), 128–131.CrossRefGoogle Scholar
Montgomery, H. L., Minimal theta functions, Glasg. Math. J. 30(1) (1988), 75–85.CrossRefGoogle Scholar
Prudnikov, A. P., Brychkov, Y. A. and Marichev, O. I., Integrals and Series, Vol. 1: Elementary Functions (Gordon and Breach, 1986).Google Scholar
Radin, C., The ground state for soft disks, J. Stat. Phys. 26 (1981), 365–373.CrossRefGoogle Scholar
Rankin, R. A., A minimum problem for the Epstein zeta function, Proc. Glasg. Math. Assoc. 1 (1953), 149–158.CrossRefGoogle Scholar
Rota Nodari, S. and Serfaty, S., Renormalized energy equidistribution and local charge balance in 2D Coulomb systems, Int. Math. Res. Not. IMRN (2014), doi:10.1093/imrn/rnu031.Google Scholar
Rougerie, N. and Serfaty, S., Higher dimensional Coulomb gases and renormalized energy functionals, Comm. Pure Appl. Math. (to appear), doi:10.1002/cpa.21570.CrossRefGoogle Scholar
Saff, E. and Kuijlaars, A., Distributing many points on a sphere, Math. Intelligencer 19(1) (1997), 5–11.CrossRefGoogle Scholar
Saff, E. B. and Totik, V., Logarithmic Potentials with External Fields, Grundlehren der mathematischen Wissenchaften, vol. 316 (Springer, Berlin, 1997).CrossRefGoogle Scholar
Sandier, E. and Serfaty, S., From the Ginzburg–Landau model to vortex lattice problems, Comm. Math. Phys. 313 (2012), 635–743.CrossRefGoogle Scholar
Sandier, E. and Serfaty, S., 2D Coulomb gases and the renormalized energy, Ann. Probab. (to appear).Google Scholar
Sandier, E. and Serfaty, S., 1D log gases and the renormalized energy: crystallization at vanishing temperature, Prob. Theor. Rel. Fields (2013), (to appear), arXiv:1303.2968, doi:10.1007/s00440-014-0585-5.CrossRefGoogle Scholar
Sarnak, P. and Strömbergsson, A., Minima of Epstein’s zeta function and heights of flat tori, Inv. Math. 165(1) (2006), 115–151.CrossRefGoogle Scholar
Serfaty, S., Coulomb Gases and Ginzburg–Landau Vortices, Zurich Lectures in Advanced Mathematics, (European Mathematical Society, 2015).CrossRefGoogle Scholar
Silvestre, L., The regularity of the obstacle problem for a fractional power of the Laplace operator, Comm. Pure Appl. Math. 60(1) (2007), 67–112.CrossRefGoogle Scholar