Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T15:05:24.483Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW COARSELY RIGID CLASS OF BANACH SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices Nonlinear functional analysis Special aspects of infinite or finite groups Graph theory

Published online by Cambridge University Press:  13 January 2020

F. Baudier ,
G. Lancien Open the ORCID record for G. Lancien [Opens in a new window] ,
P. Motakis  and
Th. Schlumprecht Open the ORCID record for Th. Schlumprecht [Opens in a new window]
F. Baudier
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX77843, USA ([email protected])
G. Lancien
Affiliation:
Laboratoire de Mathématiques de Besançon, Université Bourgogne Franche-Comté, 16 route de Gray, 25030Besançon Cédex, Besançon, France ([email protected])
P. Motakis
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL61801, USA ([email protected])
Th. Schlumprecht
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX77843-3368, USA Faculty of Electrical Engineering, Czech Technical University in Prague, Zikova 4, 16627, Prague, Czech Republic ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the class of reflexive asymptotic-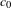$c_{0}$ Banach spaces is coarsely rigid, meaning that if a Banach space 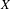$X$ coarsely embeds into a reflexive asymptotic-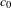$c_{0}$ space $Y$, then 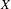$X$ is also reflexive and asymptotic-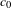$c_{0}$. In order to achieve this result, we provide a purely metric characterization of this class of Banach spaces. This metric characterization takes the form of a concentration inequality for Lipschitz maps on the Hamming graphs, which is rigid under coarse embeddings. Using an example of a quasi-reflexive asymptotic-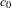$c_{0}$ space, we show that this concentration inequality is not equivalent to the non-equi-coarse embeddability of the Hamming graphs.

Keywords

Coarse embeddingscoarsely rigid classes of banach spacesasymptotic-c0 spacesHamming graphs

MSC classification

Primary: 46B06: Asymptotic theory of Banach spaces 46B20: Geometry and structure of normed linear spaces 46B85: Embeddings of discrete metric spaces into Banach spaces; applications in topology and computer science
Secondary: 46T99: None of the above, but in this section 05C63: Infinite graphs 20F65: Geometric group theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 5 , September 2021 , pp. 1729 - 1747
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

F. Baudier was supported by the National Science Foundation under Grant Number DMS-1800322. G. Lancien was supported by the French ‘Investissements d’Avenir’ program, project ISITE-BFC (contract ANR-15-IDEX-03). P. Motakis was supported by the National Science Foundation under Grant Numbers DMS-1600600 and DMS-1912897. Th. Schlumprecht was supported by the National Science Foundation under Grant Numbers DMS-1464713 and DMS-1711076.

References

Argyros, S. A., Georgiou, A., Lagos, A.-R. and Motakis, P., Joint spreading models and uniform approximation of bounded operators, Studia Math. preprint, 2018, arXiv:1712.07638, to appear.Google Scholar
Argyros, S. A., Kanellopoulos, V. and Tyros, K., Finite order spreading models, Adv. Math. 234 (2013), 574–617.Google Scholar
Baudier, F., Lancien, G. and Schlumprecht, Th., The coarse geometry of Tsirelson’s space and applications, J. Amer. Math. Soc. 31(3) (2018), 699–717.Google Scholar
Beauzamy, B. and Lapresté, J.-T., Modèles étalés des espaces de Banach, Travaux en Cours. [Works in Progress] (Hermann, Paris, 1984).Google Scholar
Bellenot, S. F., Haydon, R. and Odell, E., Quasi-reflexive and Tree Spaces Constructed in the Spirit of R. C. James, Contemporary Mathematics, Volume 85 (American Mathematical Society, Providence, RI, 1989).Google Scholar
Brunel, A. and Sucheston, L., On B-convex Banach spaces, Math. Systems Theory 7 (1974), 294–299.Google Scholar
Figiel, T. and Johnson, W. B., A uniformly convex Banach space which contains no l p, Compos. Math. 29 (1974), 179–190.Google Scholar
Freeman, D., Odell, E., Sari, B. and Zheng, B., On spreading sequences and asymptotic structures, Trans. Amer. Math. Soc. 370 (2018), 6933–6953.Google Scholar
Godefroy, G., Lancien, G. and Zizler, V., The non-linear geometry of Banach spaces after Nigel Kalton, Rocky Mountain J. Math. 44(5) (2014), 1529–1583.Google Scholar
Gromov, M., Infinite groups as geometric objects, in Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Warsaw, 1983), pp. 385–392 (PWN, Warsaw, 1984).Google Scholar
Halbeisen, L. and Odell, E., On asymptotic models in Banach spaces, Israel J. Math. 139 (2004), 253–291.Google Scholar
James, R. C., Bases and reflexivity of Banach spaces, Ann. of Math. (2) 52 (1950), 518–527.Google Scholar
James, R. C., Some self-dual properties of normed linear spaces, in Symposium on Infinite-Dimensional Topology (Louisiana State Univ., Baton Rouge, La., 1967), Annals of Mathematics Studies, 69, pp. 159–175 (Princeton University Press, Princeton, NJ, 1972).Google Scholar
Kalton, N. J., Coarse and uniform embeddings into reflexive spaces, Q. J. Math. 58 (2007), 393–414.Google Scholar
Kapovich, M., Lectures on quasi-isometric rigidity, in Geometric Group Theory, IAS/Park City Mathematics Series, Volume 21, pp. 127–172 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Knaust, H., Odell, E. and Schlumprecht, Th., On asymptotic structure, the Szlenk index and UKK properties in Banach spaces, Positivity 3 (1999), 173–199.Google Scholar
Lancien, G. and Raja, M., Asymptotic and coarse Lipschitz structures of quasi-reflexive Banach spaces, Houston J. Math 44(3) (2018), 927–940.Google Scholar
Maurey, B., Milman, V. D. and Tomczak-Jaegermann, N., Asymptotic infinite-dimensional theory of Banach spaces, in Geometric Aspects of Functional Analysis (Israel 1992), Operator Theory: Advances and Applications, Volume 77, pp. 149–175 (Birkhäuser, Basel, 1995).Google Scholar
Mendel, M. and Naor, A., Metric cotype, Ann. of Math. (2) 168 (2008), 247–298.Google Scholar
Nowak, P. W., On coarse embeddability into l p-spaces and a conjecture of Dranishnikov, Fund. Math. 189(2) (2006), 111–116.Google Scholar
Odell, E. and Schlumprecht, Th., Trees and branches in Banach spaces, Trans. Amer. Math. Soc. 354 (2002), 4085–4108 (electronic).Google Scholar
Ostrovskii, M. I., Coarse embeddability into Banach spaces, Topology Proc. 33 (2009), 163–183.Google Scholar
Randrianarivony, N. L., Characterization of quasi-Banach spaces which coarsely embed into a Hilbert space, Proc. Amer. Math. Soc. 134 (2006), 1315–1317 (electronic).Google Scholar
Tsirel’son, B. S., Not every Banach space contains an imbedding of l p or c 0, Funct. Anal. Appl. 8(2) (1974), 138–141.Google Scholar