Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T14:58:33.021Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MINIMAL MODULAR FORM ON QUATERNIONIC 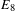$E_{8}$

Part of: Discontinuous groups and automorphic forms Linear algebraic groups and related topics

Published online by Cambridge University Press:  20 August 2020

Aaron Pollack Open the ORCID record for Aaron Pollack [Opens in a new window]
Aaron Pollack*
Affiliation:
Department of Mathematics, Duke University, Durham, NC, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that 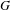$G$ is a simple reductive group over 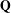$\mathbf{Q}$, with an exceptional Dynkin type and with 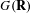$G(\mathbf{R})$ quaternionic (in the sense of Gross–Wallach). In a previous paper, we gave an explicit form of the Fourier expansion of modular forms on 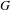$G$ along the unipotent radical of the Heisenberg parabolic. In this paper, we give the Fourier expansion of the minimal modular form 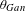$\unicode[STIX]{x1D703}_{Gan}$ on quaternionic 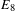$E_{8}$ and some applications. The 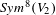$Sym^{8}(V_{2})$-valued automorphic function 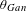$\unicode[STIX]{x1D703}_{Gan}$ is a weight 4, level one modular form on 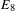$E_{8}$, which has been studied by Gan. The applications we give are the construction of special modular forms on quaternionic 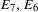$E_{7},E_{6}$ and 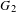$G_{2}$. We also discuss a family of degenerate Heisenberg Eisenstein series on the groups 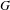$G$, which may be thought of as an analogue to the quaternionic exceptional groups of the holomorphic Siegel Eisenstein series on the groups 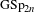$\operatorname{GSp}_{2n}$.

Keywords

minimal representationmodular formsexceptional groupsarithmetic invariant theoryEisenstein series

MSC classification

Primary: 11F03: Modular and automorphic functions
Secondary: 11F30: Fourier coefficients of automorphic forms 20G41: Exceptional groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 2 , March 2022 , pp. 603 - 636
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author has been supported by the Simons Foundation via Collaboration Grant number 585147.

References

Elkies, N. D. and Gross, B. H., The exceptional cone and the Leech lattice, Internat. Math. Res. Not. IMRN 1996(14) (1996), 665–698. MR 1411589.CrossRefGoogle Scholar
Gan, W. T., An automorphic theta module for quaternionic exceptional groups, Canad. J. Math. 52(4) (2000), 737–756. MR 1767400.CrossRefGoogle Scholar
Gan, W. T., A Siegel-Weil formula for exceptional groups, J. Reine Angew. Math. 528 (2000), 149–181. MR 1801660.Google Scholar
Gan, W. T., A regularized Siegel-Weil formula for exceptional groups, in Arithmetic Geometry and Automorphic Forms, Adv. Lect. Math. (ALM), Volume 19, pp. 155–182 (Int. Press, Somerville, MA, 2011). MR 2906908.Google Scholar
Gan, W. T. and Gross, B. H., Commutative subrings of certain non-associative rings, Math. Ann. 314(2) (1999), 265–283. MR 1697445.Google Scholar
Gan, W. T., Gross, B. and Savin, G., Fourier coefficients of modular forms on G 2 , Duke Math. J. 115(1) (2002), 105–169. MR 1932327.CrossRefGoogle Scholar
Gan, W. T. and Savin, G., On minimal representations definitions and properties, Represent. Theory 9(2005) 46–93. MR 2123125.10.1090/S1088-4165-05-00191-3CrossRefGoogle Scholar
Ginzburg, D., Rallis, S. and Soudry, D., On the automorphic theta representation for simply laced groups, Israel J. Math. 100 (1997), 61–116. MR 1469105.CrossRefGoogle Scholar
Gross, B. H. and Wallach, N. R., A distinguished family of unitary representations for the exceptional groups of real rank = 4, in Lie Theory and Geometry, Progress in Mathematics, Volume 123, pp. 289–304 (Birkhäuser, Boston, MA, 1994). MR 1327538.CrossRefGoogle Scholar
Gross, B. H. and Wallach, N. R., On quaternionic discrete series representations, and their continuations, J. Reine Angew. Math. 481 (1996), 73–123. MR 1421947.Google Scholar
Jiang, D. and Rallis, S., Fourier coefficients of Eisenstein series of the exceptional group of type G 2 , Pacific J. Math. 181(2) (1997), 281–314. MR 1486533.CrossRefGoogle Scholar
Kazhdan, D. and Polishchuk, A., Minimal representations: spherical vectors and automorphic functionals, in Algebraic Groups and Arithmetic, pp. 127–198 (Tata Inst. Fund. Res., Mumbai, 2004). MR 2094111.Google Scholar
Kim, H. H., Exceptional modular form of weight 4 on an exceptional domain contained in C27 , Rev. Mat. Iberoamericana 9(1) 139–200. MR 1216126.Google Scholar
Loke, H. Y., Restrictions of quaternionic representations, J. Funct. Anal. 172(2) (2000), 377–403. MR 1753179.CrossRefGoogle Scholar
Loke, H. Y., Quaternionic representations of exceptional Lie groups, Pacific J. Math. 211(2) (2003), 341–367. MR 2015740.CrossRefGoogle Scholar
Magaard, K. and Savin, G., Exceptional 𝛩-correspondences. I, Compositio Math. 107(1) (1997), 89–123. MR 1457344.CrossRefGoogle Scholar
Pollack, A., Lifting laws and arithmetic invariant theory, Cambridge J. Math. 6 (2018), 347–449.10.4310/CJM.2018.v6.n4.a1CrossRefGoogle Scholar
Pollack, A., The Fourier expansion of modular forms on quaternionic exceptional groups, Duke Math. J. 169(7) (2020), 1209–1280.10.1215/00127094-2019-0063CrossRefGoogle Scholar
Siegel, C. L., Einführung in die Theorie der Modulfunktionen n-ten Grades, Math. Ann. 116(1939) 617–657. MR 0001251.CrossRefGoogle Scholar
Thǎńg, N. Q., Number of connected components of groups of real points of adjoint groups, Comm. Algebra 28(3) (2000), 1097–1110. MR 1742643.Google Scholar
Wallach, N. R., Generalized Whittaker vectors for holomorphic and quaternionic representations, Comment. Math. Helv. 78(2) (2003), 266–307. MR 1988198.CrossRefGoogle Scholar