Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T13:46:30.606Z Has data issue: false hasContentIssue false
  • English
  • Français

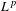$L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS

Part of: Miscellaneous topics - Partial differential equations Lie groups Integral, integro-differential, and pseudodifferential operators

Published online by Cambridge University Press:  03 April 2017

Julio Delgado  and
Michael Ruzhansky
Julio Delgado
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK ([email protected]; [email protected])
Michael Ruzhansky
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK ([email protected]; [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a compact Lie group 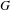$G$, in this paper we establish 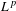$L^{p}$-bounds for pseudo-differential operators in 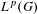$L^{p}(G)$. The criteria here are given in terms of the concept of matrix symbols defined on the noncommutative analogue of the phase space 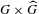$G\times \widehat{G}$, where 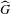$\widehat{G}$ is the unitary dual of 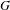$G$. We obtain two different types of 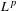$L^{p}$ bounds: first for finite regularity symbols and second for smooth symbols. The conditions for smooth symbols are formulated using 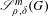$\mathscr{S}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FF}}^{m}(G)$ classes which are a suitable extension of the well-known 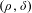$(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FF})$ ones on the Euclidean space. The results herein extend classical 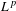$L^{p}$ bounds established by C. Fefferman on 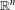$\mathbb{R}^{n}$. While Fefferman’s results have immediate consequences on general manifolds for 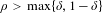$\unicode[STIX]{x1D70C}>\max \{\unicode[STIX]{x1D6FF},1-\unicode[STIX]{x1D6FF}\}$, our results do not require the condition 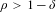$\unicode[STIX]{x1D70C}>1-\unicode[STIX]{x1D6FF}$. Moreover, one of our results also does not require 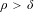$\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D6FF}$. Examples are given for the case of 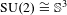$\text{SU}(2)\cong \mathbb{S}^{3}$ and vector fields/sub-Laplacian operators when operators in the classes 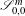$\mathscr{S}_{0,0}^{m}$ and 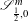$\mathscr{S}_{\frac{1}{2},0}^{m}$ naturally appear, and where conditions 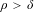$\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D6FF}$ and 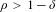$\unicode[STIX]{x1D70C}>1-\unicode[STIX]{x1D6FF}$ fail, respectively.

Keywords

compact Lie groupspseudo-differential operatorsLp bounds

MSC classification

Primary: 35S05: Pseudodifferential operators
Secondary: 22E30: Analysis on real and complex Lie groups 47G30: Pseudodifferential operators
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 3 , May 2019 , pp. 531 - 559
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Cambridge University Press 2017

Footnotes

The first author was supported by the Leverhulme Research Grant RPG-2014-02. The second author was supported by the EPSRC Grant EP/K039407/1. No new data was collected or generated during the course of research.

References

Akylzhanov, R. and Ruzhansky, M., Net spaces on lattices, Hardy–Littlewood type inequalities, and their converses, preprint, 2015, arXiv:1510.01251v1.Google Scholar
Beals, R., L p and Holder estimates for pseudodifferential operators: necessary conditions, in Harmonic Analysis in Euclidean Spaces (Proc. Symp. Pure Math., Williams Coll., Williamstown, MA, 1978), pp. 153–157 (American Mathematical Society, Providence, RI, 1979).Google Scholar
Beals, R., L p and Holder estimates for pseudodifferential operators: sufficient conditions, Ann. Inst. Fourier. 29(3) (1979), 239–260.Google Scholar
Dasgupta, A. and Ruzhansky, M., Gevrey functions and ultradistributions on compact Lie groups and homogeneous spaces, Bull. Sci. Math. 138 (2014), 756–782.Google Scholar
Dasgupta, A. and Ruzhansky, M., The Gohberg lemma, compactness, and essential spectrum of operators on compact Lie groups, J. Anal. Math. 128 (2016), 179–190.Google Scholar
Delgado, J., Estimations L p pour une classe d’opérateurs pseudo-différentiels dans le cadre du calcul de Weyl–Hörmander, J. Anal. Math. 100 (2006), 337–374.Google Scholar
Fefferman, C., L p bounds for pseudo-differential operators, Israel J. Math. 14 (1973), 413–417.Google Scholar
Fefferman, C. and Stein., E. M., H p -spaces of several variables, Acta Math. 129 (1972), 137–193.Google Scholar
Fischer, V., Intrinsic pseudo-differential calculi on any compact Lie group, J. Funct. Anal. 268 (2015), 3404–3477.Google Scholar
Fischer, V., Hörmander condition for Fourier multipliers on compact Lie groups, preprint, 2016, arXiv:1610.06348.Google Scholar
Fischer, V. and Ruzhansky, M., Fourier multipliers on graded Lie groups, preprint, 2014, arXiv:1411.6950.Google Scholar
Fischer, V. and Ruzhansky, M., Quantization on nilpotent Lie groups, Progress in Mathematics, Volume 314 (Birkhäuser, Basel, 2016).Google Scholar
Garetto, C. and Ruzhansky, M., Wave equation for sums of squares on compact Lie groups, J. Differential Equations 258(12) (2015), 4324–4347.Google Scholar
Grigor’yan, A., Estimates of heat kernels on Riemannian manifolds, in Spectral theory and geometry. ICMS Instructional Conference, Edinburgh, 1998,(ed. Davies, B. and Safarov, Yu.), London Mathematical Society Lecture Note Series, Volume 273, pp. 140–225 (Cambridge University Press, Cambridge, 1999).Google Scholar
Grigor’yan, A., Hu, J. and Lau, K.-S., Heat kernels on metric measure spaces, in Geometry and Analysis on Fractals, Springer Proceedings in Mathematics and Statistics, Volume 88, pp. 147–207 (Springer, Heidelberg, 2014).Google Scholar
Hirschman, I. I., Multiplier transformations I, Duke Math. J. 26 (1956), 222–242.Google Scholar
Hörmander, L., Pseudo-differential operators and hypoelliptic equations, in Proc. Symposium on Singular Integrals, pp. 138–183 (American Mathematical Society, vol. 10, Providence, RI, 1967).Google Scholar
Hounie, J., On the L 2 continuity of pseudo-differential operators, Communications in Partial Differential Equations 11(7) (1986), 765–778.Google Scholar
Li, Ch. and Wang, R., On the L p -boundedness of several classes of pseudo-differential operators, Chin. Ann. Math. Ser. B 5(2) (1984), 193–213.Google Scholar
Molahajloo, S. and Wong, M. W., Pseudodifferential operators on S1 , in New Developments in Pseudo-differential operators, Operator Theory: Advances and Applications, Volume 189, pp. 297–306 (Birkhäuser, Basel, 2009).Google Scholar
Nursultanov, E., Ruzhansky, M. and Tikhonov, S., Nikolskii inequality and Besov, Triebel-Lizorkin, Wiener and Beurling spaces on compact homogeneous manifolds, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) XVI(5) (2016), 981–1017.Google Scholar
Rothschild, L. and Stein, E. M., Hypoelliptic differential operators and nilpotent groups, Acta Math. 137(3–4) (1976), 247–320.Google Scholar
Ruzhansky, M. and Turunen, V., Pseudo-differential Operators and Symmetries. Background Analysis and Advanced Topics, Pseudo-Differential Operators. Theory and Applications, Volume 2 (Birkhäuser Verlag, Basel, 2010).Google Scholar
Ruzhansky, M. and Turunen, V., Sharp Gårding inequality on compact Lie groups, J. Funct. Anal. 260(10) (2011), 2881–2901.Google Scholar
Ruzhansky, M. and Turunen, V., Global quantization of pseudo-differential operators on compact Lie groups, SU(2), 3-sphere, and homogeneous spaces, Int. Math. Res. Not. IMRN 2013(11) (2013), 2439–2496.Google Scholar
Ruzhansky, M. and Wirth, J., On multipliers on compact Lie groups, Funct. Anal. Appl. 47(1) (2013), 87–91.Google Scholar
Ruzhansky, M. and Wirth, J., Global functional calculus for operators on compact Lie groups, J. Funct. Anal. 267 (2014), 144–172.Google Scholar
Ruzhansky, M. and Wirth, J., L p Fourier multipliers on compact Lie groups, Math. Z. 280 (2015), 621–642.Google Scholar
Ruzhansky, M., Turunen, V. and Wirth, J., Hörmander class of pseudo-differential operators on compact Lie groups and global hypoellipticity, J. Fourier Anal. Appl. 20 (2014), 476–499.Google Scholar
Shubin, M. A., Pseudodifferential Operators and Spectral Theory, second edition (Springer, Berlin, 2001). Translated from the 1978 Russian original by Stig I. Andersson.Google Scholar
Stein, E. M., Interpolation of linear operators, Trans. Amer. Math. Soc. 83 (1956), 482–492.Google Scholar
Stein, E. M. and Weiss, G., Introduction to Fourier Analysis on Euclidean Spaces, Princeton Mathematical Series, No. 32 (Princeton University Press, Princeton, NJ, 1971).Google Scholar
Strichartz, R., Analysis of the laplacian on the complete Riemannian manifold, J. Funct. Anal. 52 (1983), 48–79.Google Scholar
Taylor, M. E., Partial Differential Equations III. NonLinear Equations (Springer, New York, 1996).Google Scholar
Wainger, S., Special trigonometric series in k-dimensions, Mem. Amer. Math. Soc. No. 59 (1965), 102.Google Scholar
Zygmund, A., Trigonometric Series I and II, second edition (Cambridge University Press, Cambridge, New York, Melbourne, 1977).Google Scholar