Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T17:34:15.017Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCALLY ANALYTIC VECTORS AND OVERCONVERGENT 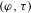$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES

Part of: Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  03 May 2019

Hui Gao  and
LĂ©o Poyeton
Hui Gao
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, FI-00014, Finland ([email protected])
LĂ©o Poyeton
Affiliation:
UMPA, École Normale SupĂ©rieure de Lyon, 46 allĂ©e d’Italie, 69007Lyon, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 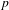$p$ be a prime, let 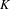$K$ be a complete discrete valuation field of characteristic $0$ with a perfect residue field of characteristic 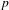$p$, and let 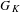$G_{K}$ be the Galois group. Let $\unicode[STIX]{x1D70B}$ be a fixed uniformizer of 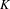$K$, let 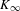$K_{\infty }$ be the extension by adjoining to 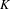$K$ a system of compatible 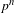$p^{n}$th roots of $\unicode[STIX]{x1D70B}$ for all $n$, and let $L$ be the Galois closure of 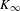$K_{\infty }$. Using these field extensions, Caruso constructs the 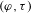$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules, which classify 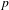$p$-adic Galois representations of 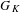$G_{K}$. In this paper, we study locally analytic vectors in some period rings with respect to the 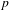$p$-adic Lie group 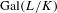$\operatorname{Gal}(L/K)$, in the spirit of the work by Berger and Colmez. Using these locally analytic vectors, and using the classical overconvergent 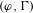$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules, we can establish the overconvergence property of the 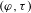$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules.

Keywords

locally analytic vectorsoverconvergence(𝜑, 𝜏)-modules

MSC classification

Primary: 11F80: Galois representations 11S20: Galois theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 137 - 185
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berger, L. and Colmez, P., Familles de reprĂ©sentations de de Rham et monodromie p-adique, AstĂ©risque (319) (2008), 303–337. ReprĂ©sentations $p$ -adiques de groupes $p$ -adiques. I. ReprĂ©sentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Berger, L. and Colmez, P., ThĂ©orie de Sen et vecteurs localement analytiques, Ann. Sci. Éc. Norm. SupĂ©r. (4) 49(4) (2016), 947–970.CrossRefGoogle Scholar
Bellovin, R., p-adic Hodge theory in rigid analytic families, Algebra Number Theory 9(2) (2015), 371–433.CrossRefGoogle Scholar
Berger, L., ReprĂ©sentations p-adiques et Ă©quations diffĂ©rentielles, Invent. Math. 148(2) (2002), 219–284.CrossRefGoogle Scholar
Berger, L., Construction de (𝜙, đ›€)-modules: reprĂ©sentations p-adiques et B-paires, Algebra Number Theory 2(1) (2008), 91–120.CrossRefGoogle Scholar
Berger, L., Galois representations and $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules. course note in IHP, 2010.Google Scholar
Berger, L., Multivariable (𝜑, đ›€)-modules and locally analytic vectors, Duke Math. J. 165(18) (2016), 3567–3595.CrossRefGoogle Scholar
Breuil, C., Une application de corps des normes, Compos. Math. 117(2) (1999), 189–203.CrossRefGoogle Scholar
Caruso, X., ReprĂ©sentations galoisiennes p-adiques et (𝜑, 𝜏)-modules, Duke Math. J. 162(13) (2013), 2525–2607.CrossRefGoogle Scholar
Cherbonnier, F. and Colmez, P., ReprĂ©sentations p-adiques surconvergentes, Invent. Math. 133(3) (1998), 581–611.CrossRefGoogle Scholar
Cherbonnier, F. and Colmez, P., ThĂ©orie d’Iwasawa des reprĂ©sentations p-adiques d’un corps local, J. Amer. Math. Soc. 12(1) (1999), 241–268.CrossRefGoogle Scholar
Colmez, P., ThĂ©orie d’Iwasawa des reprĂ©sentations de de Rham d’un corps local, Ann. of Math. (2) 148(2) (1998), 485–571.CrossRefGoogle Scholar
Colmez, P., Espaces vectoriels de dimension finie et reprĂ©sentations de de Rham, AstĂ©risque (319) (2008), 117–186. ReprĂ©sentations $p$ -adiques de groupes $p$ -adiques. I. ReprĂ©sentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Colmez, P., Fonctions d’une variable p-adique, AstĂ©risque (330) (2010), 13–59.Google Scholar
Colmez, P., ReprĂ©sentations de GL2(Q p) et (𝜙, đ›€)-modules, AstĂ©risque (330) (2010), 281–509.Google Scholar
Colmez, P., La sĂ©rie principale unitaire de GL2(Q p): vecteurs localement analytiques, in Automorphic forms and Galois representations. Vol. 1, London Math. Soc. Lecture Note Ser., volume 414, pp. 286–358 (Cambridge University Press, Cambridge, 2014).CrossRefGoogle Scholar
Fontaine, J.-M., ReprĂ©sentations p-adiques des corps locaux. I, in The Grothendieck Festschrift, Vol. II, Progr. Math., volume 87, pp. 249–309 (BirkhĂ€user Boston, Boston, MA, 1990).Google Scholar
Fontaine, J.-M. and Wintenberger, J.-P., Le “corps des normes” de certaines extensions algĂ©briques de corps locaux, C. R. Acad. Sci. Paris SĂ©r. A-B 288(6) (1979), A367–A370.Google Scholar
Gao, H. and Liu, T., Loose crystalline lifts and overconvergence of Ă©tale $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$ -modules. Amer. J. Math., to appear, arXiv:1606.07216.Google Scholar
Kedlaya, K. S., Slope filtrations revisited, Doc. Math. 10 (2005), 447–525.Google Scholar
Kisin, M., Crystalline representations and F-crystals, in Algebraic geometry and number theory, Progr. Math., volume 253, pp. 459–496 (BirkhĂ€user Boston, Boston, MA, 2006).CrossRefGoogle Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21(2) (2008), 513–546.CrossRefGoogle Scholar
Kisin, M., Integral models for Shimura varieties of abelian type, J. Amer. Math. Soc. 23(4) (2010), 967–1012.CrossRefGoogle Scholar
Kedlaya, K. and Liu, R., Relative $p$ -adic Hodge theory, II: imperfect period rings. Preprint, arXiv:1602.06899.Google Scholar
Kedlaya, K. S. and Liu, R., Relative p-adic Hodge theory: foundations, Astérisque (371) (2015), 239.Google Scholar
Le Borgne, J., Optimisation du thĂ©orĂšme d’Ax-Sen-Tate et application Ă  un calcul de cohomologie galoisienne p-adique, Ann. Inst. Fourier (Grenoble) 60(3) (2010), 1105–1123.CrossRefGoogle Scholar
Liu, T., On lattices in semi-stable representations: a proof of a conjecture of Breuil, Compos. Math. 144(1) (2008), 61–88.CrossRefGoogle Scholar
Liu, T., A note on lattices in semi-stable representations, Math. Ann. 346(1) (2010), 117–138.CrossRefGoogle Scholar
Liu, R., Xie, B. and Zhang, Y., Locally analytic vectors of unitary principal series of GL2(ℚp), Ann. Sci. Éc. Norm. SupĂ©r. (4) 45(1) (2012), 167–190.CrossRefGoogle Scholar
Serre, J.-P., Lie algebras and Lie groups, Lecture Notes in Mathematics, volume 1500 (Springer, Berlin, 2006). 1964 lectures given at Harvard University, Corrected fifth printing of the second (1992) edition.Google Scholar
Schneider, P. and Teitelbaum, J., Locally analytic distributions and p-adic representation theory, with applications to GL2 , J. Amer. Math. Soc. 15(2) (2002), 443–468.CrossRefGoogle Scholar
Wintenberger, J.-P., Le corps des normes de certaines extensions infinies de corps locaux; applications, Ann. Sci. Éc. Norm. SupĂ©r. (4) 16(1) (1983), 59–89.CrossRefGoogle Scholar