Article contents
LOCALIZATION BY 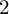 $2$-PERIODIC COMPLEXES AND VIRTUAL STRUCTURE SHEAVES
$2$-PERIODIC COMPLEXES AND VIRTUAL STRUCTURE SHEAVES
Published online by Cambridge University Press: 22 December 2020
Abstract
In [12], Kim and the first author proved a result comparing the virtual fundamental classes of the moduli spaces of 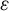 $\varepsilon $
-stable quasimaps and
$\varepsilon $
-stable quasimaps and 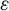 $\varepsilon $
-stable
$\varepsilon $
-stable 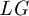 $LG$
-quasimaps by studying localized Chern characters for
$LG$
-quasimaps by studying localized Chern characters for 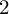 $2$
-periodic complexes.
$2$
-periodic complexes.
In this paper, we study a K-theoretic analogue of the localized Chern character map and show that for a Koszul 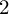 $2$
-periodic complex it coincides with the cosection-localized Gysin map of Kiem and Li [11]. As an application, we compare the virtual structure sheaves of the moduli space of
$2$
-periodic complex it coincides with the cosection-localized Gysin map of Kiem and Li [11]. As an application, we compare the virtual structure sheaves of the moduli space of 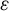 $\varepsilon $
-stable quasimaps and
$\varepsilon $
-stable quasimaps and 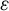 $\varepsilon $
-stable
$\varepsilon $
-stable 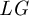 $LG$
-quasimaps.
$LG$
-quasimaps.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1477 - 1506
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 2
- Cited by



