Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-29T04:01:57.186Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL VANISHING AND HODGE FILTRATION FOR RATIONAL SINGULARITIES

Part of: Surfaces and higher-dimensional varieties (Co)homology theory Singularities

Published online by Cambridge University Press:  17 May 2018

Mircea Mustaţă ,
Sebastián Olano  and
Mihnea Popa
Mircea Mustaţă
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA ([email protected])
Sebastián Olano
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208, USA ([email protected]; [email protected])
Mihnea Popa
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208, USA ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an $n$-dimensional variety 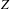$Z$ with rational singularities, we conjecture that if 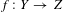$f:Y\rightarrow Z$ is a resolution of singularities whose reduced exceptional divisor 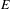$E$ has simple normal crossings, then

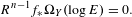$$\begin{eqnarray}\displaystyle R^{n-1}f_{\ast }\unicode[STIX]{x1D6FA}_{Y}(\log E)=0. & & \displaystyle \nonumber\end{eqnarray}$$
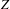We prove this when $Z$ has isolated singularities and when it is a toric variety. We deduce that for a divisor 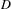$D$ with isolated rational singularities on a smooth complex $n$-dimensional variety 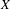$X$, the generation level of Saito’s Hodge filtration on the localization 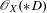$\mathscr{O}_{X}(\ast D)$ is at most $n-3$.

Keywords

rational singularitiesvanishing theoremsHodge ideals

MSC classification

Primary: 14J17: Singularities 14F17: Vanishing theorems 32S25: Surface and hypersurface singularities 32S35: Mixed Hodge theory of singular varieties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 3 , May 2020 , pp. 801 - 819
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

MM was partially supported by NSF grant DMS-1401227; MP was partially supported by NSF grant DMS-1405516.

References

de Cataldo, M. A. A. and Migliorini, L., The Hodge theory of algebraic maps, Ann. Sci. Éc. Norm. Supér. (4) 38(5) (2005), 693–750.Google Scholar
de Cataldo, M. A. A. and Migliorini, L., Intersection forms, topology of maps and motivic decomposition for resolutions of threefolds, in Algebraic Cycles and Motives, Vol. 1, London Mathematical Society Lecture Note Series, Volume 343, pp. 102–137 (Cambridge University Press, Cambridge, 2007).10.1017/CBO9780511721496.004Google Scholar
Cattani, E., El Zein, F., Griffiths, P. A. and Lê, D. T. (Eds.) Hodge Theory, Mathematical Notes, Volume 49, p. xviii+589 (Princeton University Press, Princeton, NJ, 2014).Google Scholar
Elkik, R., Singularités rationnelles et déformations, Invent. Math. 47(2) (1978), 139–147.10.1007/BF01578068Google Scholar
Elzein, F., Mixed Hodge structures, in Singularities, Part 1 (Arcata, CA, 1981), Proceedings of Symposia in Pure Mathematics, Volume 40, pp. 345–352 (American Mathematical Society, Providence, RI, 1983).Google Scholar
Esnault, H. and Viehweg, E., Revêtements cycliques, in Algebraic Threefolds (Varenna 1981), Lecture Notes in Mathematics, Volume 947, pp. 241–250 (Springer, Berlin–New York, 1982).Google Scholar
Fulton, W., Introduction to toric varieties, in The William H. Roever Lectures in Geometry, Annals of Mathematics Studies, Volume 131 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Greb, D., Kebekus, S., Kovács, S. J. and Peternell, T., Differential forms on log canonical spaces, Publ. Math. Inst. Hautes Études Sci. 114 (2011), 87–169.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, No. 52, p. xvi+496 (Springer-Verlag, New York–Heidelberg, 1977).Google Scholar
Jow, S. Y. and Miller, E., Multiplier ideals of sums via cellular resolutions, Math. Res. Lett. 15(2) (2008), 359–373.10.4310/MRL.2008.v15.n2.a13Google Scholar
Kovács, S., Rational, log canonical, Du Bois singularities: on the conjectures of Kollár and Steenbrink, Compositio Math. 118 (1999), 123–133.Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry II, in Ergebnisse der Mathematik und ihrer Grenzgebiete, Volume 49 (Springer-Verlag, Berlin, 2004).Google Scholar
Mustaţă, M. and Popa, M., Hodge ideals, Mem. Amer. Math. Soc. (to appear). Preprint, 2016, arXiv:1605.08088.Google Scholar
Mustaţă, M. and Popa, M., Restriction, subadditivity, and semicontinuity theorems for Hodge ideals, Int. Math. Res. Not. IMRN (to appear). Preprint, 2016, arXiv:1606.05659.10.1093/imrn/rnw343Google Scholar
Saito, M., Mixed Hodge modules, Publ. Res. Inst. Math. Sci. 26(2) (1990), 221–333.Google Scholar
Saito, M., On b-function, spectrum and rational singularity, Math. Ann. 295(1) (1993), 51–74.10.1007/BF01444876Google Scholar
Saito, M., On the Hodge filtration of Hodge modules, Mosc. Math. J. 9(1) (2009), 161–191.Google Scholar
Steenbrink, J. H. M., Mixed Hodge structures associated with isolated singularities, in Singularities, Part 2 (Arcata, CA, 1981), Proceedings of Symposia in Pure Mathematics, Volume 40, pp. 513–536 (American Mathematical Society, Providence, RI, 1983).Google Scholar
Takagi, S., Formulas for multiplier ideals on singular varieties, Amer. J. Math. 128(6) (2006), 1345–1362.10.1353/ajm.2006.0049Google Scholar