Article contents
LOCAL DECAY FOR THE DAMPED WAVE EQUATION IN THE ENERGY SPACE
Published online by Cambridge University Press: 01 April 2016
Abstract
We improve a previous result about the local energy decay for the damped wave equation on 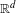 $\mathbb{R}^{d}$. The problem is governed by a Laplacian associated with a long-range perturbation of the flat metric and a short-range absorption index. Our purpose is to recover the decay
$\mathbb{R}^{d}$. The problem is governed by a Laplacian associated with a long-range perturbation of the flat metric and a short-range absorption index. Our purpose is to recover the decay 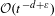 ${\mathcal{O}}(t^{-d+\unicode[STIX]{x1D700}})$ in the weighted energy spaces. The proof is based on uniform resolvent estimates, given by an improved version of the dissipative Mourre theory. In particular, we have to prove the limiting absorption principle for the powers of the resolvent with inserted weights.
${\mathcal{O}}(t^{-d+\unicode[STIX]{x1D700}})$ in the weighted energy spaces. The proof is based on uniform resolvent estimates, given by an improved version of the dissipative Mourre theory. In particular, we have to prove the limiting absorption principle for the powers of the resolvent with inserted weights.
Keywords
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 3 , June 2018 , pp. 509 - 540
- Copyright
- © Cambridge University Press 2016
References
- 5
- Cited by


