Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T08:28:59.911Z Has data issue: false hasContentIssue false
  • English
  • Français

LINEAR SYSTEMS ON IRREGULAR VARIETIES

Part of: Cycles and subschemes Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  12 March 2019

Miguel Ángel Barja Open the ORCID record for Miguel Ángel Barja [Opens in a new window] ,
Rita Pardini Open the ORCID record for Rita Pardini [Opens in a new window]  and
Lidia Stoppino Open the ORCID record for Lidia Stoppino [Opens in a new window]
Miguel Ángel Barja
Affiliation:
Departament de Matemàtiques, Universitat Politècnica de Catalunya, Avda. Diagonal 647, 08028Barcelona, Spain ([email protected])
Rita Pardini
Affiliation:
Dipartimento di Matematica, Università di Pisa, Largo B. Pontecorvo 5, I-56127 Pisa, Italy ([email protected])
Lidia Stoppino
Affiliation:
Dipartimento di Matematica, Università di Pavia, Via Ferrata 5, 27100, Pavia, Italy ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

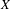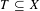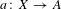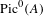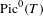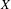Let $X$ be a normal complex projective variety, $T\subseteq X$ a subvariety of dimension $m$ (possibly $T=X$) and $a:X\rightarrow A$ a morphism to an abelian variety such that $\text{Pic}^{0}(A)$ injects into $\text{Pic}^{0}(T)$; let $L$ be a line bundle on $X$ and 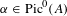$\unicode[STIX]{x1D6FC}\in \text{Pic}^{0}(A)$ a general element.

We introduce two new ingredients for the study of linear systems on 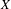$X$. First of all, we show the existence of a factorization of the map $a$, called the eventual map of $L$ on $T$, which controls the behavior of the linear systems 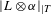$|L\otimes \unicode[STIX]{x1D6FC}|_{|T}$, asymptotically with respect to the pullbacks to the connected étale covers 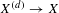$X^{(d)}\rightarrow X$ induced by the 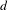$d$-th multiplication map of $A$.

Second, we define the so-called continuous rank function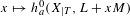$x\mapsto h_{a}^{0}(X_{|T},L+xM)$, where 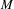$M$ is the pullback of an ample divisor of $A$. This function extends to a continuous function of 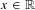$x\in \mathbb{R}$, which is differentiable except possibly at countably many points; when 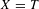$X=T$ we compute the left derivative explicitly.

As an application, we give quick short proofs of a wide range of new Clifford–Severi inequalities, i.e., geographical bounds of the form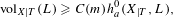

$$\begin{eqnarray}\displaystyle \text{vol}_{X|T}(L)\geqslant C(m)h_{a}^{0}(X_{|T},L), & & \displaystyle \nonumber\end{eqnarray}$$
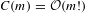where $C(m)={\mathcal{O}}(m!)$ depends on several geometrical properties of 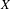$X$, $L$ or $a$.

Keywords

irregular varietyvariety of maximal Albanese dimensioneventual mapcontinuous rank functionClifford-Severi inequalities

MSC classification

Primary: 14C20: Divisors, linear systems, invertible sheaves
Secondary: 14J29: Surfaces of general type 14J30: $3$-folds 14J35: $4$-folds 14J40: $n$-folds ($n>4$)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 6 , November 2020 , pp. 2087 - 2125
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by MINECO MTM2015-69135-P “Geometría y Topología de Variedades, Álgebra y Aplicaciones” and by Generalitat de Catalunya SGR2014-634. The second and third authors are members of G.N.S.A.G.A.–I.N.d.A.M. This research was partially supported by MIUR (Italy) through PRIN 2010–11 “Geometria delle varietà algebriche” and PRIN 2012–13 “Moduli, strutture geometriche e loro applicazioni”.

References

Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J., Geometry of Algebraic Curves. I, Grundlehren der Mathematischen Wissenschaften, Volume 267 (Springer, New York, 1985).Google Scholar
Barja, M. A., Generalized Clifford Severi inequality and the volume of irregular varieties, Duke Math. J. 164(3) (2015), 541–568.10.1215/00127094-2871306Google Scholar
Barja, M. A., Pardini, R. and Stoppino, L., Surfaces on the Severi line, J. Math. Pures Appl. (5) (2016), 734–743.10.1016/j.matpur.2015.11.012Google Scholar
Barja, M. A., Pardini, R. and Stoppino, L., The eventual paracanonical map of a variety of maximal Albanese dimension, Algebraic Geom., to appear.Google Scholar
Barja, M. A., Pardini, R. and Stoppino, L., Higher dimensional Clifford–Severi equalities, Preprint, 2018, arXiv:mathAG/1806.03005.Google Scholar
Birkenhake, C. and Lange, H., Complex Abelian Varieties, 2nd ed., Grundlehren der Mathematischen Wissenschaften, Volume 302 (Springer, Berlin, 2004).Google Scholar
Boucksom, S., Favre, C. and Jonsson, M., Differentiability of volumes of divisors and a problem of Teissier, J. Algebraic Geom. 18(2) (2009), 279–308.Google Scholar
Castorena, A. and Pirola, G., Some results on deformation of sections of vector bundles, Collect. Math. 68(1) (2017), 9–20.10.1007/s13348-016-0169-zGoogle Scholar
Catanese, F., Moduli of surfaces of general type, in Algebraic Geometry: Open Problems. Proc. Ravello 1982, Lecture Notes in Mathematics, Volume 997, pp. 90–112 (Springer, Berlin, Heidelberg, New York, 1983).Google Scholar
Catanese, F., On the moduli spaces of surfaces of general type, J. Differential Geom. 19 (1984), 483–515.Google Scholar
Chen, J. A., Chen, M. and Zhang, D. Q., The 5-canonical system on 3-folds of general type, J. Reine Angew. Math. 603 (2007), 165–181.Google Scholar
Debarre, O., On coverings of simple abelian varieties, Bull. Soc. Math. France 134(2) (2006), 253–260.Google Scholar
Ein, L. and Lazarsfeld, R., Singularities of Theta divisors, and birational geometry of irregular varieties, J. Amer. Math. Soc. 10(1) (1997), 243–258.Google Scholar
Ein, L., Lazarsfeld, R., Popa, M., Mustata, M. and Nakamaye, M., Restricted volumes and base loci of linear series, Amer. J. Math. 131 (2009), 607–651.Google Scholar
Fulton, W. and Lazarsfeld, R., Connectivity and its applications in Algebraic Geometry, in Algebraic Geometry (Chicago, 1980), Lecture Notes in Mathematics, Volume 862, pp. 26–92 (Springer, Berlin, 1981).10.1007/BFb0090889Google Scholar
Green, M. and Lazarsfeld, R., Deformation theory, generic vanishing theorems, and some conjectures of Enriques, Catanese and Beauville, Invent. Math. 90 (1987), 416–440.Google Scholar
Hacon, C. D., McKernan, J. and Xu, C., On the birational automorphisms of varieties of general type, Ann. of Math. (2) 177 (2013), 1077–1111.10.4007/annals.2013.177.3.6Google Scholar
Holschbach, A., A Chebotarev type density theorem in algebraic geometry, PhD thesis, University of Pennsylvania. ProQuest LLC, Ann Arbor, MI (2008). 72 pp.Google Scholar
Manetti, M., Surfaces of Albanese general type and the Severi conjecture, Math. Nachr. 261–262 (2003), 105–122.Google Scholar
Jiang, Z., Some results on the eventual paracanonical maps, Preprint, 2016, arXiv:1611.07141 [math.AG].Google Scholar
Jiang, Z. and Pareschi, B., Cohomological rank functions on abelian varieties, Ann. Sci. Éc. Norm. Supér. (4), 2017, to appear, arXiv:1707.05888 [math.AG].Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. I, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 48 (Springer, Berlin, 2004).Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. II, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 49 (Springer, Berlin, 2004).Google Scholar
Lazarsfeld, R. and Mustata, M., Convex bodies associated to linear series, Ann. Sci. Éc. Norm. Supér. (4) 42(5) (2009), 783–835.10.24033/asens.2109Google Scholar
Lu, X. and Zuo, K., On the Severi type Inequalities for Irregular Surfaces, Int. Math. Res. Note. IMRN 2019(1) 231–248.10.1093/imrn/rnx127Google Scholar
Pardini, R., Abelian covers of algebraic varieties, J. Reine Angew. Math. 417 (1991), 191–213.Google Scholar
Pardini, R., The Severi inequality K 2⩾4𝜒 for surfaces of maximal Albanese dimension, Invent. Math. 159(3) (2005), 669–672.Google Scholar
Pareschi, B. and Popa, M., GV sheaves, Fourier–Mukai transforms and Generic Vanishing, Amer. J. Math. 133(1) (2011), 235–271.Google Scholar
Pareschi, B. and Popa, M., Generic vanishing and minimal cohomology classes on abelian varieties, Math. Ann. 340(1) (2008), 209–222.Google Scholar
Pareschi, B. and Popa, M., M-regularity and the Fourier–Mukai transform, Pure Appl. Math. Q. 4 (2008), 587–611. 3, Special Issue: In honor of Fedor Bogomolov. Part 2.Google Scholar
Pareschi, B. and Popa, M., Regularity on abelian varieties III: relationship with generic vanishing and applications, in Grassmannians, Moduli Spaces and Vector Bundles, Clay Math. Proc., Volume 14, pp. 141–167 (Amer. Math. Soc., Providence, RI, 2011).Google Scholar
Reid, M., 𝜋1 for Surfaces with Small c 12, Lecture Notes in Mathematics, Volume 732, pp. 534–544 (Springer, Belin, Heidelberg, New York, 1978).Google Scholar
Severi, F., La serie canonica e la teoria delle serie principali di gruppi di punti sopra una superficie algebrica, Comment. Math. Helv. 4 (1932), 268–326.Google Scholar
Xiao, G., Fibered algebraic surfaces with low slope, Math. Ann. 276 (1987), 449–466.Google Scholar
Zhang, T., Severi inequality for varieties of maximal Albanese dimension, Math. Ann. 359(3) (2014), 1097–1114.Google Scholar