1. Introduction
For the once-punctured torus, the Thurston compactification of the Teichmüller space by projective measured laminations coincides with the visual compactification of the hyperbolic plane. In this case, every geodesic ray has a unique limit point, and the dynamical behavior of the ray in moduli space is governed by the continued fraction of its limit point. For hyperbolic surfaces of higher complexity, Teichmüller space with the Teichmüller metric is no longer negatively curved [Reference MasurMas75, Reference Masur and WolfMW95] (or even Riemannian), and the Thurston boundary is no longer its visual boundary [Reference KerckhoffKer80]. More surprisingly, geodesic rays do not always converge [Reference LenzhenLen08, Reference Leininger, Lenzhen and RafiLLR18].
For hyperbolic surfaces of higher complexity, another interesting phenomenon is the existence of nontrivial simplices in the Thurston boundary which correspond to measures on nonuniquely ergodic laminations. Particularly interesting is the case when the underlying lamination is minimal and filling, also called arational. Constructions of nonuniquely ergodic arational laminations have a long history and typically used flat structures on surfaces [Reference VeechVee69, Reference SataevSat75, Reference Keynes and NewtonKN76, Reference KeaneKea77]. A topological construction was introduced in [Reference GabaiGab09]. In [Reference Leininger, Lenzhen and RafiLLR18], Leininger, Lenzhen and Rafi combined this topological approach with some arithmetic parameters akin to continued fractions. This allowed them to show that it is possible for the full simplex of measures on a nonuniquely ergodic arational lamination to be realized as the limit set of a Teichmüller geodesic ray.
In this paper, we take the above construction into Culler–Vogtmann’s Outer space [Reference Culler and VogtmannCV86]. A Thurston-type boundary for Outer space is given by the set of projective classes of minimal, very small
![]() ${\mathbb {F}_{n}}$
-trees [Reference Culler and MorganCM87, Reference Bestvina and FeighnBF94, Reference Cohen and LustigCL95, Reference HorbezHor17] and the action of
${\mathbb {F}_{n}}$
-trees [Reference Culler and MorganCM87, Reference Bestvina and FeighnBF94, Reference Cohen and LustigCL95, Reference HorbezHor17] and the action of
![]() $\operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
extends continuously to the compactified space. The analogue of arational laminations are arational trees; for example, trees dual to arational laminations on a once-punctured surface fall into this category. There are other examples, such as trees dual to minimal laminations on finite 2-complexes that are not surfaces, called Levitt type; and yet others, called nongeometric, that do not come from the latter two constructions. The nonuniquely ergodic phenomenon for laminations has two natural analogues for
$\operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
extends continuously to the compactified space. The analogue of arational laminations are arational trees; for example, trees dual to arational laminations on a once-punctured surface fall into this category. There are other examples, such as trees dual to minimal laminations on finite 2-complexes that are not surfaces, called Levitt type; and yet others, called nongeometric, that do not come from the latter two constructions. The nonuniquely ergodic phenomenon for laminations has two natural analogues for
![]() ${\mathbb {F}_{n}}$
-trees: one in terms of length measures on trees, giving rise to nonuniquely ergometric trees [Reference GuirardelGui00] and the other in terms of currents, giving nonuniquely ergodic trees; see [Reference Coulbois, Hilion and LustigCHL07]. It is an open problem to determine whether these two notions coincide. An example of a nonuniquely ergometric arational tree of Levitt type, modeled on Keane’s construction, was given in [Reference MartinMar97]. In this paper, we construct the first nongeometric example of an arational tree that is neither uniquely ergodic nor uniquely ergometric.
${\mathbb {F}_{n}}$
-trees: one in terms of length measures on trees, giving rise to nonuniquely ergometric trees [Reference GuirardelGui00] and the other in terms of currents, giving nonuniquely ergodic trees; see [Reference Coulbois, Hilion and LustigCHL07]. It is an open problem to determine whether these two notions coincide. An example of a nonuniquely ergometric arational tree of Levitt type, modeled on Keane’s construction, was given in [Reference MartinMar97]. In this paper, we construct the first nongeometric example of an arational tree that is neither uniquely ergodic nor uniquely ergometric.
In Outer space, the analogue of Teichmüller metric is the Lipschitz metric and that of Teichmüller geodesics are folding paths. However, unlike Teichmüller geodesics, a folding path in Outer space has a forward direction, reflecting the asymmetry of the Lipschitz metric. Even though the boundary of Outer space is not a visual boundary, a folding path always converges along its forward direction. Our main result is that this nice behavior does not persist in the backward direction; in fact, in the backward direction, folding paths can behave as badly as Teichmüller geodesics. Define an unfolding path in Outer space to be a folding path with the backward direction. Our main result, as follows, is a direct analogue of the results of [Reference Leininger, Lenzhen and RafiLLR18].
Theorem 1.1. There exists an unfolding path in Outer space of free group of rank 7 which does not converge to a point in the boundary of Outer space. In fact, the limit set is a 1-simplex consisting of the full set of length measures on a nongeometric and arational tree T. Moreover, the set of projective currents dual to T is also a one-dimensional simplex. In particular, T is neither uniquely ergometric nor uniquely ergodic.
We use the framework of folding and unfolding sequences. Every such sequence tracks the combinatorics of an appropriate folding path, resp. unfolding path, in Outer space. An infinite folding sequence has a naturally associated limiting tree in the boundary of Outer space and an unfolding sequence has a naturally associated algebraic lamination, called the legal lamination. The graphs in the folding sequence can be given compatible metrics, which are then used to parametrize the different length measures supported on the limiting tree. Compatible edge thicknesses on the graphs of the unfolding sequence parametrize the different currents with support contained in the legal lamination. The latter can then be used to study the currents dual to the trees in the limit set of the unfolding sequence. See [Reference Namazi, Pettet and ReynoldsNPR14] or our Section 3 for definitions and more precise statements.
Modeling the construction of [Reference Leininger, Lenzhen and RafiLLR18] on a five-holed sphere, the folding and unfolding sequences we consider come from explicit sequences of automorphisms of the free group of rank 7. More explicitly, fix a nongeometric fully irreducible automorphism on three letters and extend it to an automorphism
![]() $\phi $
of
$\phi $
of
![]() ${\mathbb {F}_{7}}$
by identity on the other four basis elements. Also, let
${\mathbb {F}_{7}}$
by identity on the other four basis elements. Also, let
![]() $\rho $
be a finite-order automorphism of
$\rho $
be a finite-order automorphism of
![]() ${\mathbb {F}_{7}}$
that rotates the support of
${\mathbb {F}_{7}}$
that rotates the support of
![]() $\phi $
off itself. For an integer r, set
$\phi $
off itself. For an integer r, set
![]() $\phi _r = \rho \phi ^r$
. Given a sequence
$\phi _r = \rho \phi ^r$
. Given a sequence
![]() $(r_i)_{i \ge 1}$
of positive integers, define a sequence of automorphisms by
$(r_i)_{i \ge 1}$
of positive integers, define a sequence of automorphisms by
From
![]() $(\Phi _i)_i$
, we get an unfolding sequence using the train track map induced by
$(\Phi _i)_i$
, we get an unfolding sequence using the train track map induced by
![]() $\phi _{r_i}$
, and from
$\phi _{r_i}$
, and from
![]() $(\Phi _i^{-1})_i$
we get a companion folding sequence. The parameters
$(\Phi _i^{-1})_i$
we get a companion folding sequence. The parameters
![]() $(r_i)_i$
play the role of the continued fraction expansion for the limiting tree of the folding sequence, and adjusting them produces different types of trees and behaviors of the unfolding sequence. In particular, we show that if the sequence
$(r_i)_i$
play the role of the continued fraction expansion for the limiting tree of the folding sequence, and adjusting them produces different types of trees and behaviors of the unfolding sequence. In particular, we show that if the sequence
![]() $(r_i)_i$
satisfies certain arithmetic conditions and grows sufficiently fast, then the limiting tree is arational, nongeometric, nonuniquely ergodic and nonuniquely ergometric. Moreover, the limit set of the unfolding sequence is the full simplex of length measures on the tree. We refer to Theorem 10 for the full technical statement.
$(r_i)_i$
satisfies certain arithmetic conditions and grows sufficiently fast, then the limiting tree is arational, nongeometric, nonuniquely ergodic and nonuniquely ergometric. Moreover, the limit set of the unfolding sequence is the full simplex of length measures on the tree. We refer to Theorem 10 for the full technical statement.
To see how the parameters
![]() $(r_i)_i$
come into play, it is informative to look at the sequence of free factors
$(r_i)_i$
come into play, it is informative to look at the sequence of free factors
![]() $A_i = \Phi _i(A)$
, where A is the support of
$A_i = \Phi _i(A)$
, where A is the support of
![]() $\phi $
. The
$\phi $
. The
![]() $A_i$
’s are the projection of the folding sequence to the free factor complex
$A_i$
’s are the projection of the folding sequence to the free factor complex
![]() ${\mathcal {FF}_{7}}$
. By our construction,
${\mathcal {FF}_{7}}$
. By our construction,
![]() $A_i$
and
$A_i$
and
![]() $A_{i+1}$
are disjoint (meaning
$A_{i+1}$
are disjoint (meaning
![]() ${\mathbb {F}_{7}}=A_i*A_{i+1}*B_i$
for some
${\mathbb {F}_{7}}=A_i*A_{i+1}*B_i$
for some
![]() $B_i$
), but
$B_i$
), but
![]() $A_i, A_{i+2}$
are not, and
$A_i, A_{i+2}$
are not, and
![]() $r_i$
measures the distance between the projections of
$r_i$
measures the distance between the projections of
![]() $A_{i-2}$
and
$A_{i-2}$
and
![]() $A_{i+2}$
to the free factor complex of
$A_{i+2}$
to the free factor complex of
![]() $A_i$
. Morally, if
$A_i$
. Morally, if
![]() $r_i$
’s are sufficiently large, then
$r_i$
’s are sufficiently large, then
![]() $(A_i)_i$
forms a quasi-geodesic in
$(A_i)_i$
forms a quasi-geodesic in
![]() ${\mathcal {FF}_{7}}$
. Hence, by [Reference Bestvina and ReynoldsBR15, Reference HamenstädtHam16], the limiting tree of the folding sequence is arational. In addition, we show that the tree is nongeometric. To get two currents on the tree, we take loops in the
${\mathcal {FF}_{7}}$
. Hence, by [Reference Bestvina and ReynoldsBR15, Reference HamenstädtHam16], the limiting tree of the folding sequence is arational. In addition, we show that the tree is nongeometric. To get two currents on the tree, we take loops in the
![]() $A_i$
’s, which correspond to currents on
$A_i$
’s, which correspond to currents on
![]() ${\mathbb {F}_{n}}$
and take projective limits of the odd and even subsequences. Nonunique ergometricity of the tree follows a similar principle.
${\mathbb {F}_{n}}$
and take projective limits of the odd and even subsequences. Nonunique ergometricity of the tree follows a similar principle.
Although our construction is general in spirit, the case of rank 7 is already fairly involved, and some computations used computer assistance. One issue is that there is no known algorithm to tell if a collection of free factors has a common complement. This issue appears in the proof of arationality of the limiting tree that led to the peculiar looking arithmetic conditions on the parameters; see Section 5.
Outline
-
• In Section 2, we review some background material, including train track maps, Outer space, currents, length measures and arational trees.
-
• In Section 3, we discuss folding and unfolding sequences. We relate length measures on a folding sequence with the length measures on the limiting tree when it is arational. We also define the legal lamination for an unfolding sequence and state a result from [Reference Namazi, Pettet and ReynoldsNPR14] relating the currents supported on the legal lamination with those of the unfolding sequence.
-
• In Section 4, we discuss our main construction to generate from a sequence
 $(r_i)_i$
of positive integers a sequence of automorphisms of
$(r_i)_i$
of positive integers a sequence of automorphisms of
 ${\mathbb {F}_{7}}$
. The associated transition matrices for these automorphisms have block shapes which we use to analyze their asymptotic behavior. From each sequence of automorphisms and their inverses, we get a folding and unfolding sequence of graphs of rank 7 induced by their train track maps.
${\mathbb {F}_{7}}$
. The associated transition matrices for these automorphisms have block shapes which we use to analyze their asymptotic behavior. From each sequence of automorphisms and their inverses, we get a folding and unfolding sequence of graphs of rank 7 induced by their train track maps. -
• In Section 5, we show that under the right conditions on
 $(r_i)_i$
, the folding sequence converges to a nongeometric and arational tree T in boundary of Outer space of rank 7. To show arationality, we project the folding sequence to the free factor complex and show it is a quasi-geodesic.
$(r_i)_i$
, the folding sequence converges to a nongeometric and arational tree T in boundary of Outer space of rank 7. To show arationality, we project the folding sequence to the free factor complex and show it is a quasi-geodesic. -
• In Section 6, we study the behavior of the unfolding sequence. The main result is that if the sequence
 $(r_i)_i$
grows sufficiently fast, then the legal lamination of the unfolding sequence supports a 1-simplex of projective currents.
$(r_i)_i$
grows sufficiently fast, then the legal lamination of the unfolding sequence supports a 1-simplex of projective currents. -
• In Section 7, we show that if the sequence
 $(r_i)_i$
grows sufficiently fast, then the limiting tree of the folding sequence supports a 1-simplex of projective length measures. In particular, the limiting tree is not uniquely ergometric.
$(r_i)_i$
grows sufficiently fast, then the limiting tree of the folding sequence supports a 1-simplex of projective length measures. In particular, the limiting tree is not uniquely ergometric. -
• In Section 8, we relate the legal lamination of the unfolding sequence to the dual lamination of the limiting tree of the folding sequence. This shows the limiting tree is not uniquely ergodic.
-
• In Section 9, we show that the unfolding sequence limits onto the full simplex of length measures on the limiting tree of the folding sequence, and thus does not have a unique limit in the boundary of Outer space.
-
• In Section 10, we collect the results to prove the main theorem.
-
• In Section A, we prove a technical lemma about convergence of products of matrices.
2. Background
Let
![]() ${\mathbb {F}_{n}}$
be the free group of rank n. We review some background on train track maps, Outer space, laminations, currents, arational trees and the free factor complex.
${\mathbb {F}_{n}}$
be the free group of rank n. We review some background on train track maps, Outer space, laminations, currents, arational trees and the free factor complex.
2.1. Train track maps
We recall some basic definitions from [Reference Bestvina and HandelBH92]. Identify
![]() ${\mathbb {F}_{n}}$
with
${\mathbb {F}_{n}}$
with
![]() $\pi _1(\mathrm {R}_n, \ast )$
, where
$\pi _1(\mathrm {R}_n, \ast )$
, where
![]() $\mathrm {R}_n$
is a rose with n petals. A marked graph G is a graph of rank n, all of whose vertices have valence at least three, equipped with a homotopy equivalence
$\mathrm {R}_n$
is a rose with n petals. A marked graph G is a graph of rank n, all of whose vertices have valence at least three, equipped with a homotopy equivalence
![]() $m\colon \, \mathrm {R}_n \to G$
called a marking.
$m\colon \, \mathrm {R}_n \to G$
called a marking.
A length vector on G is a vector
![]() $\lambda \in {\mathbb R}^{|EG|}$
that assigns a positive number, that is, a length, to every edge of G. The volume of G with respect to
$\lambda \in {\mathbb R}^{|EG|}$
that assigns a positive number, that is, a length, to every edge of G. The volume of G with respect to
![]() $\lambda $
is the total length of all the edges of G. This induces a path metric on G where the length of an edge e is
$\lambda $
is the total length of all the edges of G. This induces a path metric on G where the length of an edge e is
![]() $\lambda (e)$
.
$\lambda (e)$
.
A direction d based at a vertex
![]() $v \in G$
is an oriented edge of G with initial vertex v. A turn is an unordered pair of distinct directions based at the same vertex. A train track structure on G is an equivalence relation on the set of directions at each vertex
$v \in G$
is an oriented edge of G with initial vertex v. A turn is an unordered pair of distinct directions based at the same vertex. A train track structure on G is an equivalence relation on the set of directions at each vertex
![]() $v \in G$
. The classes of this relation are called gates. A turn
$v \in G$
. The classes of this relation are called gates. A turn
![]() $(d,d')$
is legal if d and
$(d,d')$
is legal if d and
![]() $d'$
do not belong to the same gate, it is called illegal otherwise. A path is legal if it only crosses legal turns.
$d'$
do not belong to the same gate, it is called illegal otherwise. A path is legal if it only crosses legal turns.
A map
![]() $f \colon \, G \to G'$
between two graphs is called a morphism if it is locally injective on open edges and sends vertices to vertices. If G and
$f \colon \, G \to G'$
between two graphs is called a morphism if it is locally injective on open edges and sends vertices to vertices. If G and
![]() $G'$
are metric graphs, then we can homotope f relative to vertices such that it is linear on edges. Similarly, for an
$G'$
are metric graphs, then we can homotope f relative to vertices such that it is linear on edges. Similarly, for an
![]() ${\mathbb R}$
-tree T, a map
${\mathbb R}$
-tree T, a map
![]() $\tilde G\to T$
from the universal cover of G is a morphism if it is injective on open edges. To a morphism
$\tilde G\to T$
from the universal cover of G is a morphism if it is injective on open edges. To a morphism
![]() $f\colon \, G \to G'$
we associate the transition matrix as follows: Enumerate the (unoriented) edges
$f\colon \, G \to G'$
we associate the transition matrix as follows: Enumerate the (unoriented) edges
![]() $e_1,e_2,\cdots ,e_m$
of G and
$e_1,e_2,\cdots ,e_m$
of G and
![]() $e_1', e_2', \cdots , e_n'$
of
$e_1', e_2', \cdots , e_n'$
of
![]() $G'$
. Then the transition matrix M has size
$G'$
. Then the transition matrix M has size
![]() $n\times m$
and the
$n\times m$
and the
![]() $ij$
-entry is the number of times
$ij$
-entry is the number of times
![]() $f(e_j)$
crosses
$f(e_j)$
crosses
![]() $e_i'$
, that is, it is the cardinality of the set
$e_i'$
, that is, it is the cardinality of the set
![]() $f^{-1}(x)\cap e_j$
for a point x in the interior of
$f^{-1}(x)\cap e_j$
for a point x in the interior of
![]() $e_i'$
. If f is in addition a homotopy equivalence, then f is a change-of-marking.
$e_i'$
. If f is in addition a homotopy equivalence, then f is a change-of-marking.
A homotopy equivalence
![]() $f\colon \, G \to G$
induces an outer automorphism of
$f\colon \, G \to G$
induces an outer automorphism of
![]() $\pi _1(G)$
and hence an element
$\pi _1(G)$
and hence an element
![]() $\phi $
of
$\phi $
of
![]() $\operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
. If f is a morphism, then we say that f is a topological representative of
$\operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
. If f is a morphism, then we say that f is a topological representative of
![]() $\phi $
. A topological representative
$\phi $
. A topological representative
![]() $f \colon \, G\to G$
induces a train track structure on G as follows: The map f determines a map
$f \colon \, G\to G$
induces a train track structure on G as follows: The map f determines a map
![]() $Df$
on the directions in G by defining
$Df$
on the directions in G by defining
![]() $Df(e)$
to be the first (oriented) edge in the edge path
$Df(e)$
to be the first (oriented) edge in the edge path
![]() $f(e)$
. We then declare
$f(e)$
. We then declare
![]() $e_1\sim e_2$
if
$e_1\sim e_2$
if
![]() $(Df)^k(e_1)=(Df)^k(e_2)$
for some
$(Df)^k(e_1)=(Df)^k(e_2)$
for some
![]() $k\geq 1$
.
$k\geq 1$
.
A topological representative
![]() $f\colon \, G \to G$
is called a train track map if every vertex has at least two gates, and f maps legal turns to legal turns and legal paths (equivalently, edges) to legal paths. Equivalently, every positive power
$f\colon \, G \to G$
is called a train track map if every vertex has at least two gates, and f maps legal turns to legal turns and legal paths (equivalently, edges) to legal paths. Equivalently, every positive power
![]() $f^k$
is a topological representative. If f is a train track map with transition matrix M, then the transition matrix of
$f^k$
is a topological representative. If f is a train track map with transition matrix M, then the transition matrix of
![]() $f^k$
is
$f^k$
is
![]() $M^k$
for every
$M^k$
for every
![]() $k\geq 1$
. If M is primitive, that is,
$k\geq 1$
. If M is primitive, that is,
![]() $M^k$
has positive entries for some
$M^k$
has positive entries for some
![]() $k \ge 1$
, then Perron–Frobenius theory implies that there is an assignment of positive lengths to all the edges of G so that f uniformly expands lengths of legal paths by some factor
$k \ge 1$
, then Perron–Frobenius theory implies that there is an assignment of positive lengths to all the edges of G so that f uniformly expands lengths of legal paths by some factor
![]() $\lambda>1$
, called the stretch factor of f.
$\lambda>1$
, called the stretch factor of f.
If
![]() $\sigma $
is a path (or a circuit) in G, we denote by
$\sigma $
is a path (or a circuit) in G, we denote by
![]() $[\sigma ]$
the reduced path homotopic to
$[\sigma ]$
the reduced path homotopic to
![]() $\sigma $
(rel endpoints if
$\sigma $
(rel endpoints if
![]() $\sigma $
is a path). A path or circuit
$\sigma $
is a path). A path or circuit
![]() $\sigma $
in G is called a periodic Nielsen path if
$\sigma $
in G is called a periodic Nielsen path if
![]() $[f^k(\sigma )]=\sigma $
for some
$[f^k(\sigma )]=\sigma $
for some
![]() $k\geq 1$
. If
$k\geq 1$
. If
![]() $k=1$
, then
$k=1$
, then
![]() $\sigma $
is a Nielsen path. A Nielsen path that cannot be written as a concatenation of nontrivial Nielsen paths is called an indivisible Nielsen path, denoted INP.
$\sigma $
is a Nielsen path. A Nielsen path that cannot be written as a concatenation of nontrivial Nielsen paths is called an indivisible Nielsen path, denoted INP.
The following lemma is an important property of train track maps. For a very rudimentary form, see [Reference Bestvina and HandelBH92, Lemma 3.4] showing that INPs have exactly one illegal turn, and for a more involved version see [Reference Bestvina, Feighn and HandelBFH97] (some details can also be found in [Reference Kapovich and LustigKL14, Proposition 3.27, 3.28]). We will need it for the proof of Lemma 4.8 and include a proof here.
Lemma 2.1. Let
![]() $h\colon \, G \to G$
be a train track map with a primitive transition matrix. There exists a constant
$h\colon \, G \to G$
be a train track map with a primitive transition matrix. There exists a constant
![]() $R>0$
such that for any edge path
$R>0$
such that for any edge path
![]() $\gamma $
, either
$\gamma $
, either
-
1. the number of illegal turns in
 $[h^{R}(\gamma )]$
is less than that of
$[h^{R}(\gamma )]$
is less than that of
 $\gamma $
, or
$\gamma $
, or -
2.
 $\gamma = u_1 v_1 u_2 v_2 \ldots u_n$
, where each
$\gamma = u_1 v_1 u_2 v_2 \ldots u_n$
, where each
 $u_i$
is a legal subpath, possibly degenerate, and each
$u_i$
is a legal subpath, possibly degenerate, and each
 $[h^{R}(v_i)]$
is a periodic INP.
$[h^{R}(v_i)]$
is a periodic INP.
Proof. Let
![]() $\lambda> 1$
be the stretch factor of h, and equip G with the metric so that h uniformly expands the length of every legal path by
$\lambda> 1$
be the stretch factor of h, and equip G with the metric so that h uniformly expands the length of every legal path by
![]() $\lambda $
. It goes back to the work of Thurston (see [Reference CooperCoo87]) that there is a constant
$\lambda $
. It goes back to the work of Thurston (see [Reference CooperCoo87]) that there is a constant
![]() $BCC(h)$
, called the bounded cancellation constant for h, such that if
$BCC(h)$
, called the bounded cancellation constant for h, such that if
![]() $\alpha \beta $
is a reduced edge path, then
$\alpha \beta $
is a reduced edge path, then
![]() $[h(\alpha )][h(\beta )]$
have cancellation bounded by
$[h(\alpha )][h(\beta )]$
have cancellation bounded by
![]() $BCC(h)$
. The existence of this constant is really a consequence of the Morse lemma and the fact that h is a quasi-isometry. Define
$BCC(h)$
. The existence of this constant is really a consequence of the Morse lemma and the fact that h is a quasi-isometry. Define
![]() $C = BCC(h) / (\lambda -1)$
.
$C = BCC(h) / (\lambda -1)$
.
Here is the significance of C. To fix ideas, let us assume that
![]() $\gamma $
has only one illegal turn, so
$\gamma $
has only one illegal turn, so
![]() $\gamma =\alpha \beta $
with both
$\gamma =\alpha \beta $
with both
![]() $\alpha ,\beta $
legal. Say
$\alpha ,\beta $
legal. Say
![]() $\alpha $
has length
$\alpha $
has length
![]() $|\alpha |=C+\epsilon>C$
. Then
$|\alpha |=C+\epsilon>C$
. Then
![]() $h(\alpha )$
has length
$h(\alpha )$
has length
![]() $\lambda |\alpha |$
and after cancellation with
$\lambda |\alpha |$
and after cancellation with
![]() $h(\beta )$
the length is
$h(\beta )$
the length is
![]() $\geq \lambda |\alpha | -BCC(h)=|\alpha |+\lambda \epsilon $
. Thus, assuming
$\geq \lambda |\alpha | -BCC(h)=|\alpha |+\lambda \epsilon $
. Thus, assuming
![]() $[h^i(\gamma )]$
still has an illegal turn, the length of the initial subpath to the illegal turn has length growing exponentially in i, assuming it is long enough.
$[h^i(\gamma )]$
still has an illegal turn, the length of the initial subpath to the illegal turn has length growing exponentially in i, assuming it is long enough.
We now prove the lemma for paths
![]() $\gamma =\alpha \beta $
with one illegal turn and with
$\gamma =\alpha \beta $
with one illegal turn and with
![]() $\alpha ,\beta $
legal. Consider the finite collection of paths consisting of those with length at most C with both endpoints at vertices or with length exactly C with only one endpoint at a vertex. Let R be a number larger than the square of the size of this collection. If
$\alpha ,\beta $
legal. Consider the finite collection of paths consisting of those with length at most C with both endpoints at vertices or with length exactly C with only one endpoint at a vertex. Let R be a number larger than the square of the size of this collection. If
![]() $[h^i(\gamma )]=\alpha _i\beta _i$
has one illegal turn (with
$[h^i(\gamma )]=\alpha _i\beta _i$
has one illegal turn (with
![]() $\alpha _i,\beta _i$
legal) for
$\alpha _i,\beta _i$
legal) for
![]() $i=1,2,\cdots ,R$
, then by the pigeon-hole principle there will be
$i=1,2,\cdots ,R$
, then by the pigeon-hole principle there will be
![]() $i<j$
in this range so that the C-neighborhoods of the illegal turns of
$i<j$
in this range so that the C-neighborhoods of the illegal turns of
![]() $[h^i(\gamma )]$
and
$[h^i(\gamma )]$
and
![]() $[h^j(\gamma )]$
are the same (if
$[h^j(\gamma )]$
are the same (if
![]() $\alpha _i$
or
$\alpha _i$
or
![]() $\beta _i$
has length
$\beta _i$
has length
![]() $<C$
this means
$<C$
this means
![]() $\alpha _i=\alpha _j$
or
$\alpha _i=\alpha _j$
or
![]() $\beta _i=\beta _j$
). We can lift
$\beta _i=\beta _j$
). We can lift
![]() $h^{j-i}$
and
$h^{j-i}$
and
![]() $\gamma $
to the universal cover of the graph and arrange that (the lift of)
$\gamma $
to the universal cover of the graph and arrange that (the lift of)
![]() $\gamma $
and
$\gamma $
and
![]() $[h^{j-i}(\gamma )]$
have the same illegal turn. Thus,
$[h^{j-i}(\gamma )]$
have the same illegal turn. Thus,
![]() $h^{j-i}$
maps the terminal C-segment of
$h^{j-i}$
maps the terminal C-segment of
![]() $\alpha _i$
(or
$\alpha _i$
(or
![]() $\alpha _i$
itself) over itself (by the above calculation) and therefore fixes a point in
$\alpha _i$
itself) over itself (by the above calculation) and therefore fixes a point in
![]() $\alpha _i$
and similarly for
$\alpha _i$
and similarly for
![]() $\beta _i$
. The subpath of
$\beta _i$
. The subpath of
![]() $[h^i(\gamma )]$
between these fixed points is a periodic INP, proving the lemma in the case
$[h^i(\gamma )]$
between these fixed points is a periodic INP, proving the lemma in the case
![]() $\gamma $
has one illegal turn.
$\gamma $
has one illegal turn.
The general case is similar. Write
![]() $\gamma =\gamma _1\gamma _2\cdots \gamma _s$
with all
$\gamma =\gamma _1\gamma _2\cdots \gamma _s$
with all
![]() $\gamma _k$
legal and with the turn between
$\gamma _k$
legal and with the turn between
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k+1}$
illegal. Also, assume that
$\gamma _{k+1}$
illegal. Also, assume that
![]() $[h^i(\gamma )]$
has the same number of illegal turns for
$[h^i(\gamma )]$
has the same number of illegal turns for
![]() $i=1,\cdots ,R$
. We can write
$i=1,\cdots ,R$
. We can write
![]() $[h^i(\gamma )]=\gamma _1^i\gamma _2^i\cdots \gamma _s^i$
with all
$[h^i(\gamma )]=\gamma _1^i\gamma _2^i\cdots \gamma _s^i$
with all
![]() $\gamma _k^i$
legal and the turns between them illegal. For each illegal turn corresponding to the pair
$\gamma _k^i$
legal and the turns between them illegal. For each illegal turn corresponding to the pair
![]() $(k,k+1)$
, there will be
$(k,k+1)$
, there will be
![]() $i<j$
in this range so that the C-neighborhoods of the illegal turn in
$i<j$
in this range so that the C-neighborhoods of the illegal turn in
![]() $[h^i(\gamma )]$
and in
$[h^i(\gamma )]$
and in
![]() $[h^j(\gamma )]$
are the same. This gives fixed points of
$[h^j(\gamma )]$
are the same. This gives fixed points of
![]() $h^{j-i}$
in
$h^{j-i}$
in
![]() $\gamma _k^i$
and
$\gamma _k^i$
and
![]() $\gamma _{k+1}^i$
, and these fixed points split
$\gamma _{k+1}^i$
, and these fixed points split
![]() $\gamma $
into periodic INPs and legal segments, as claimed.
$\gamma $
into periodic INPs and legal segments, as claimed.
We will use the lemma in the situation that h has no periodic INPs, in which case the conclusion is that whenever
![]() $\gamma $
is not legal, then
$\gamma $
is not legal, then
![]() $[h^{R}(\gamma )]$
has fewer illegal turns than
$[h^{R}(\gamma )]$
has fewer illegal turns than
![]() $\gamma $
.
$\gamma $
.
2.2. Outer space and its boundary
An
![]() ${\mathbb {F}_{n}}$
-tree is an
${\mathbb {F}_{n}}$
-tree is an
![]() $\mathbb {R}$
-tree with an isometric action of
$\mathbb {R}$
-tree with an isometric action of
![]() ${\mathbb {F}_{n}}$
. An
${\mathbb {F}_{n}}$
. An
![]() ${\mathbb {F}_{n}}$
-tree T has dense orbits if some (every) orbit is dense in T. An
${\mathbb {F}_{n}}$
-tree T has dense orbits if some (every) orbit is dense in T. An
![]() ${\mathbb {F}_{n}}$
-tree is called very small if the action is minimal, arc stabilizers are either trivial or maximal cyclic and tripod stabilizers are trivial. We review the definition of Outer space first introduced in [Reference Culler and VogtmannCV86].
${\mathbb {F}_{n}}$
-tree is called very small if the action is minimal, arc stabilizers are either trivial or maximal cyclic and tripod stabilizers are trivial. We review the definition of Outer space first introduced in [Reference Culler and VogtmannCV86].
Unprojectivized Outer space, denoted by
![]() ${\text {cv}_{n}} $
, is the set of free, minimal and simplicial
${\text {cv}_{n}} $
, is the set of free, minimal and simplicial
![]() ${\mathbb {F}_{n}}$
-trees. By considering the quotient graphs,
${\mathbb {F}_{n}}$
-trees. By considering the quotient graphs,
![]() ${\text {cv}_{n}} $
is also equivalently the set of marked metric graphs, that is, the set of triples
${\text {cv}_{n}} $
is also equivalently the set of marked metric graphs, that is, the set of triples
![]() $(G,m,\lambda )$
, where G is a graph of rank n with all valences at least
$(G,m,\lambda )$
, where G is a graph of rank n with all valences at least
![]() $3$
,
$3$
,
![]() $m\colon \, \mathrm {R}_n \to G$
is a marking and
$m\colon \, \mathrm {R}_n \to G$
is a marking and
![]() $\lambda $
is a positive length vector on G. By [Reference Culler and MorganCM87], the map of
$\lambda $
is a positive length vector on G. By [Reference Culler and MorganCM87], the map of
![]() ${\text {cv}_{n}} \to {\mathbb R}^{{\mathbb {F}_{n}}}$
given by
${\text {cv}_{n}} \to {\mathbb R}^{{\mathbb {F}_{n}}}$
given by
![]() $T \mapsto (\left \lVert g\right \rVert _T)_{g \in {\mathbb {F}_{n}}}$
, where
$T \mapsto (\left \lVert g\right \rVert _T)_{g \in {\mathbb {F}_{n}}}$
, where
![]() $\left \lVert g\right \rVert _T$
is the translation length of g in T, is an inclusion. This endows
$\left \lVert g\right \rVert _T$
is the translation length of g in T, is an inclusion. This endows
![]() ${\text {cv}_{n}} $
with a topology. The closure
${\text {cv}_{n}} $
with a topology. The closure
![]() ${\overline {\text {cv}}_{n}}$
in
${\overline {\text {cv}}_{n}}$
in
![]() ${\mathbb R}^{{\mathbb {F}_{n}}}$
is the space of very small
${\mathbb R}^{{\mathbb {F}_{n}}}$
is the space of very small
![]() ${\mathbb {F}_{n}}$
-trees [Reference Bestvina and FeighnBF94, Reference Cohen and LustigCL95]. The boundary
${\mathbb {F}_{n}}$
-trees [Reference Bestvina and FeighnBF94, Reference Cohen and LustigCL95]. The boundary
![]() $\partial {\text {cv}_{n}} = {\overline {\text {cv}}_{n}}-{\text {cv}_{n}} $
consists of very small trees that are either not free or not simplicial.
$\partial {\text {cv}_{n}} = {\overline {\text {cv}}_{n}}-{\text {cv}_{n}} $
consists of very small trees that are either not free or not simplicial.
Culler Vogtmann’s Outer space,
![]() ${\text {CV}_{n}} $
, is the image of
${\text {CV}_{n}} $
, is the image of
![]() ${\text {cv}_{n}} $
in the projective space
${\text {cv}_{n}} $
in the projective space
![]() ${\mathbb P}{\mathbb R}^{{\mathbb {F}_{n}}}$
. Elements in
${\mathbb P}{\mathbb R}^{{\mathbb {F}_{n}}}$
. Elements in
![]() ${\text {CV}_{n}} $
can also be described as free, minimal, simplicial
${\text {CV}_{n}} $
can also be described as free, minimal, simplicial
![]() ${\mathbb {F}_{n}}$
-trees with unit covolume. Topologically,
${\mathbb {F}_{n}}$
-trees with unit covolume. Topologically,
![]() ${\text {CV}_{n}} $
is a complex made up of simplices with missing faces, where there is an open simplex for each marked graph
${\text {CV}_{n}} $
is a complex made up of simplices with missing faces, where there is an open simplex for each marked graph
![]() $(G,m)$
spanned by positive length vectors on G of unit volume. The closure
$(G,m)$
spanned by positive length vectors on G of unit volume. The closure
![]() ${\overline {\text {CV}}_{n}}$
of
${\overline {\text {CV}}_{n}}$
of
![]() ${\text {CV}_{n}} $
in
${\text {CV}_{n}} $
in
![]() ${\mathbb P}{\mathbb R}^{{\mathbb {F}_{n}}}$
is compact and the boundary
${\mathbb P}{\mathbb R}^{{\mathbb {F}_{n}}}$
is compact and the boundary
![]() $\partial {\text {CV}_{n}} = {\overline {\text {CV}}_{n}} -{\text {CV}_{n}} $
is the projectivization of
$\partial {\text {CV}_{n}} = {\overline {\text {CV}}_{n}} -{\text {CV}_{n}} $
is the projectivization of
![]() $\partial {\overline {\text {cv}}_{n}}$
.
$\partial {\overline {\text {cv}}_{n}}$
.
The spaces
![]() ${\text {cv}_{n}} $
and
${\text {cv}_{n}} $
and
![]() ${\text {CV}_{n}} $
and their closures are equipped with a natural (right) action by
${\text {CV}_{n}} $
and their closures are equipped with a natural (right) action by
![]() $\operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
. That is, for
$\operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
. That is, for
![]() $\Phi \in \operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
and
$\Phi \in \operatorname {\mathrm {Out}}({\mathbb {F}_{n}})$
and
![]() $T \in {\overline {\text {cv}}_{n}}$
the translation length function of
$T \in {\overline {\text {cv}}_{n}}$
the translation length function of
![]() $T \Phi $
on
$T \Phi $
on
![]() ${\mathbb {F}_{n}}$
is
${\mathbb {F}_{n}}$
is
![]() $\left \lVert g\right \rVert _{T \Phi } = \left \lVert \phi (g)\right \rVert _T$
, where
$\left \lVert g\right \rVert _{T \Phi } = \left \lVert \phi (g)\right \rVert _T$
, where
![]() $\phi $
is any lift of
$\phi $
is any lift of
![]() $\Phi $
to
$\Phi $
to
![]() $\operatorname {\mathrm {Aut}}({\mathbb {F}_{n}})$
.
$\operatorname {\mathrm {Aut}}({\mathbb {F}_{n}})$
.
2.3. Laminations, currents and nonuniquely ergodic trees
In [Reference Bestvina, Feighn and HandelBFH00], Bestvina, Feighn and Handel defined a dynamical invariant called the attracting lamination associated to a train track map. In this article, we will consider the more modern definition of a lamination as given in [Reference Coulbois, Hilion and LustigCHL08a].
Let
![]() $\partial {\mathbb {F}_{n}}$
denote the Gromov boundary of
$\partial {\mathbb {F}_{n}}$
denote the Gromov boundary of
![]() ${\mathbb {F}_{n}}$
, and let
${\mathbb {F}_{n}}$
, and let
![]() $\Delta $
be the diagonal in
$\Delta $
be the diagonal in
![]() $\partial {\mathbb {F}_{n}} \times \partial {\mathbb {F}_{n}}$
. The double boundary of
$\partial {\mathbb {F}_{n}} \times \partial {\mathbb {F}_{n}}$
. The double boundary of
![]() ${\mathbb {F}_{n}}$
is
${\mathbb {F}_{n}}$
is
![]() $\partial ^2 {\mathbb {F}_{n}} = (\partial {\mathbb {F}_{n}} \times \partial {\mathbb {F}_{n}} - \Delta ) / \mathbb {Z}_2$
, which parametrizes the space of unoriented bi-infinite geodesics in a Cayley graph of
$\partial ^2 {\mathbb {F}_{n}} = (\partial {\mathbb {F}_{n}} \times \partial {\mathbb {F}_{n}} - \Delta ) / \mathbb {Z}_2$
, which parametrizes the space of unoriented bi-infinite geodesics in a Cayley graph of
![]() ${\mathbb {F}_{n}}$
. By an (algebraic) lamination, we mean a nonempty, closed and
${\mathbb {F}_{n}}$
. By an (algebraic) lamination, we mean a nonempty, closed and
![]() ${\mathbb {F}_{n}}$
-invariant subset of
${\mathbb {F}_{n}}$
-invariant subset of
![]() $\partial ^2 {\mathbb {F}_{n}}$
.
$\partial ^2 {\mathbb {F}_{n}}$
.
Associated to
![]() $T\in {\overline {\text {cv}}_{n}}$
is a dual lamination
$T\in {\overline {\text {cv}}_{n}}$
is a dual lamination
![]() $L(T)$
, defined as follows in [Reference Coulbois, Hilion and LustigCHL08b]. For
$L(T)$
, defined as follows in [Reference Coulbois, Hilion and LustigCHL08b]. For
![]() $\epsilon> 0$
, let
$\epsilon> 0$
, let
so
![]() $L_{\epsilon }(T)$
is a lamination and set
$L_{\epsilon }(T)$
is a lamination and set
![]() $L(T) = \bigcap _{\epsilon>0}L_{\epsilon }(T)$
. Elements of
$L(T) = \bigcap _{\epsilon>0}L_{\epsilon }(T)$
. Elements of
![]() $L(T)$
are called leaves. For trees in
$L(T)$
are called leaves. For trees in
![]() ${\text {cv}_{n}} $
,
${\text {cv}_{n}} $
,
![]() $L(T)$
is empty.
$L(T)$
is empty.
A current is an additive, nonnegative,
![]() ${\mathbb {F}_{n}}$
-invariant function on the set of compact open sets in
${\mathbb {F}_{n}}$
-invariant function on the set of compact open sets in
![]() $\partial ^2 {\mathbb {F}_{n}}$
. Equivalently, it is an
$\partial ^2 {\mathbb {F}_{n}}$
. Equivalently, it is an
![]() ${\mathbb {F}_{n}}$
-invariant Radon measure on the
${\mathbb {F}_{n}}$
-invariant Radon measure on the
![]() $\sigma $
-algebra of Borel sets of
$\sigma $
-algebra of Borel sets of
![]() $\partial ^2 {\mathbb {F}_{n}}$
. Let
$\partial ^2 {\mathbb {F}_{n}}$
. Let
![]() ${\mathrm {Curr}_{n}}$
denote the space of currents, equipped with the weak* topology. The quotient space of
${\mathrm {Curr}_{n}}$
denote the space of currents, equipped with the weak* topology. The quotient space of
![]() ${\mathbb {P}\mathrm {Curr}_{n}}$
of projectivized currents (i.e., homothety classes of nonzero currents) is compact.
${\mathbb {P}\mathrm {Curr}_{n}}$
of projectivized currents (i.e., homothety classes of nonzero currents) is compact.
For
![]() $\mu \in {\mathrm {Curr}_{n}}$
, let
$\mu \in {\mathrm {Curr}_{n}}$
, let
![]() $\text {supp}(\mu ) \subset \partial ^2 {\mathbb {F}_{n}}$
denote the support of
$\text {supp}(\mu ) \subset \partial ^2 {\mathbb {F}_{n}}$
denote the support of
![]() $\mu $
, which is in fact a lamination. For
$\mu $
, which is in fact a lamination. For
![]() $T \in {\overline {\text {cv}}_{n}}$
and
$T \in {\overline {\text {cv}}_{n}}$
and
![]() $\mu \in {\mathrm {Curr}_{n}}$
, if
$\mu \in {\mathrm {Curr}_{n}}$
, if
![]() $\text {supp}(\mu ) \subseteq L(T)$
, then we say
$\text {supp}(\mu ) \subseteq L(T)$
, then we say
![]() $\mu $
is dual to T. Denote by
$\mu $
is dual to T. Denote by
![]() $\text {Curr}(T)$
the convex cone of currents dual to T and by
$\text {Curr}(T)$
the convex cone of currents dual to T and by
![]() ${\mathbb P}\text {Curr}(T)$
the set of projective currents dual to T.
${\mathbb P}\text {Curr}(T)$
the set of projective currents dual to T.
![]() ${\mathbb P}\text {Curr}(T)$
is a compact, convex space and its extremal points are called the ergodic currents dual to T. We say T is uniquely ergodic if there is only one projective class of currents dual to T, and nonuniquely ergodic otherwise. In [Reference Coulbois and HilionCH16], the authors show that if
${\mathbb P}\text {Curr}(T)$
is a compact, convex space and its extremal points are called the ergodic currents dual to T. We say T is uniquely ergodic if there is only one projective class of currents dual to T, and nonuniquely ergodic otherwise. In [Reference Coulbois and HilionCH16], the authors show that if
![]() $T \in \partial {\text {cv}_{n}} $
has dense orbits, then
$T \in \partial {\text {cv}_{n}} $
has dense orbits, then
![]() ${\mathbb P}\text {Curr}(T)$
is the convex hull of at most
${\mathbb P}\text {Curr}(T)$
is the convex hull of at most
![]() $3n-5$
projective classes of ergodic currents dual to T.
$3n-5$
projective classes of ergodic currents dual to T.
In [Reference Kapovich and LustigKL09], Kapovich and Lustig established a length pairing,
![]() $\langle \cdot , \cdot \rangle $
, between
$\langle \cdot , \cdot \rangle $
, between
![]() ${\overline {\text {cv}}_{n}}$
and the space of measured currents
${\overline {\text {cv}}_{n}}$
and the space of measured currents
![]() ${\mathrm {Curr}_{n}}$
. They also showed in [Reference Kapovich and LustigKL10, Theorem 1.1] that for
${\mathrm {Curr}_{n}}$
. They also showed in [Reference Kapovich and LustigKL10, Theorem 1.1] that for
![]() $T \in {\overline {\text {cv}}_{n}}$
and
$T \in {\overline {\text {cv}}_{n}}$
and
![]() $\mu \in {\mathrm {Curr}_{n}}$
,
$\mu \in {\mathrm {Curr}_{n}}$
,
![]() $\langle T, \mu \rangle = 0$
if and only if
$\langle T, \mu \rangle = 0$
if and only if
![]() $\mu $
is dual to T.
$\mu $
is dual to T.
Given two trees T and
![]() $T'$
, we say a map
$T'$
, we say a map
![]() $h\colon \, T \to T'$
is alignment-preserving if whenever
$h\colon \, T \to T'$
is alignment-preserving if whenever
![]() $b \in T$
is contained in an arc
$b \in T$
is contained in an arc
![]() $[a,c] \subset T$
, then
$[a,c] \subset T$
, then
![]() $h(b)$
is contained in the arc
$h(b)$
is contained in the arc
![]() $[h(a),h(c)]$
.
$[h(a),h(c)]$
.
Theorem 2.2 [Reference Coulbois, Hilion and LustigCHL07]
Let
![]() $T, T' \in \partial {\text {CV}_{n}} $
be two trees with dense orbits. The following are equivalent:
$T, T' \in \partial {\text {CV}_{n}} $
be two trees with dense orbits. The following are equivalent:
-
•
 $L(T) = L(T')$
.
$L(T) = L(T')$
. -
• There exists an
 ${\mathbb {F}_{n}}$
-equivariant alignment-preserving bijection between T and
${\mathbb {F}_{n}}$
-equivariant alignment-preserving bijection between T and
 $T'$
.
$T'$
.
2.4. Length measures and nonuniquely ergometric trees
Since
![]() ${\mathbb R}$
-trees need not be locally compact, classical measure theory is not well suited for them. In [Reference PaulinPau95], a length measure was introduced for
${\mathbb R}$
-trees need not be locally compact, classical measure theory is not well suited for them. In [Reference PaulinPau95], a length measure was introduced for
![]() ${\mathbb R}$
-trees. See [Reference GuirardelGui00] for details.
${\mathbb R}$
-trees. See [Reference GuirardelGui00] for details.
A length measure on an
![]() ${\mathbb {F}_{n}}$
-tree T is a collection of finite Borel measures
${\mathbb {F}_{n}}$
-tree T is a collection of finite Borel measures
![]() $\lambda _I$
for every compact interval I in T such that if
$\lambda _I$
for every compact interval I in T such that if
![]() $J \subset I$
, then
$J \subset I$
, then
![]() $\lambda _J = (\lambda _I)|_J$
. We require the length measure to be invariant under the
$\lambda _J = (\lambda _I)|_J$
. We require the length measure to be invariant under the
![]() ${\mathbb {F}_{n}}$
action. The collection of the Lebesgue measures of the intervals of T is
${\mathbb {F}_{n}}$
action. The collection of the Lebesgue measures of the intervals of T is
![]() ${\mathbb {F}_{n}}$
-invariant, and this will be called the Lebesgue measure of T. A length measure
${\mathbb {F}_{n}}$
-invariant, and this will be called the Lebesgue measure of T. A length measure
![]() $\lambda $
is nonatomic or positive if every
$\lambda $
is nonatomic or positive if every
![]() $\lambda _I$
is nonatomic or positive. If every orbit is dense in some segment of T, then T cannot have an invariant measure with atoms. Further, if T is indecomposable, that is, if for any pair of nondegenerate arcs I and J in T, there exist
$\lambda _I$
is nonatomic or positive. If every orbit is dense in some segment of T, then T cannot have an invariant measure with atoms. Further, if T is indecomposable, that is, if for any pair of nondegenerate arcs I and J in T, there exist
![]() $g_1,\ldots ,g_m \in {\mathbb {F}_{n}}$
such that
$g_1,\ldots ,g_m \in {\mathbb {F}_{n}}$
such that
![]() $I \subset \bigcup g_iJ$
and
$I \subset \bigcup g_iJ$
and
![]() $g_i J \cap g_{i+1} J$
is nondegenerate, then every nonzero length measure is positive (in fact, the condition of mixing [Reference GuirardelGui00] suffices).
$g_i J \cap g_{i+1} J$
is nondegenerate, then every nonzero length measure is positive (in fact, the condition of mixing [Reference GuirardelGui00] suffices).
Let
![]() ${\mathcal D}(T)$
be the cone of
${\mathcal D}(T)$
be the cone of
![]() ${\mathbb {F}_{n}}$
-invariant length measures on T, with projectivization
${\mathbb {F}_{n}}$
-invariant length measures on T, with projectivization
![]() ${\mathbb P}{\mathcal D}(T)$
, that is, the homothety classes of
${\mathbb P}{\mathcal D}(T)$
, that is, the homothety classes of
![]() ${\mathbb {F}_{n}}$
-invariant length measures on T.
${\mathbb {F}_{n}}$
-invariant length measures on T.
![]() ${\mathbb P}{\mathcal D}(T)$
is a compact convex set and we will call its extremal points the ergodic length measures on T. When T has dense orbits there are at most
${\mathbb P}{\mathcal D}(T)$
is a compact convex set and we will call its extremal points the ergodic length measures on T. When T has dense orbits there are at most
![]() $3n-4$
such measures for any T (see [Reference GuirardelGui00, Corollary 5.2, Lemma 5.3]) and
$3n-4$
such measures for any T (see [Reference GuirardelGui00, Corollary 5.2, Lemma 5.3]) and
![]() ${\mathcal D}(T)$
is naturally a subset of
${\mathcal D}(T)$
is naturally a subset of
![]() $\partial cv_n$
. In fact,
$\partial cv_n$
. In fact,
Lemma 2.3. [Reference GuirardelGui00] If
![]() $T \in {\text {cv}_{n}} $
is indecomposable, then
$T \in {\text {cv}_{n}} $
is indecomposable, then
![]() $\mathcal {D}(T)$
is in one-to-one correspondence with the set of isometry classes of
$\mathcal {D}(T)$
is in one-to-one correspondence with the set of isometry classes of
![]() ${\mathbb {F}_{n}}$
-invariant metrics on T, denoted
${\mathbb {F}_{n}}$
-invariant metrics on T, denoted
![]() $X_T \subset {\text {cv}_{n}} $
.
$X_T \subset {\text {cv}_{n}} $
.
Proof. Let
![]() $\lambda \in \mathcal {D}(T)$
be a length measure on T. Consider the pseudo-metric
$\lambda \in \mathcal {D}(T)$
be a length measure on T. Consider the pseudo-metric
![]() $d_{\lambda }$
on T, where
$d_{\lambda }$
on T, where
![]() $d_{\lambda }(x,y) = \lambda ([x,y])$
for
$d_{\lambda }(x,y) = \lambda ([x,y])$
for
![]() $x, y \in T$
. In fact, since T is indecomposable,
$x, y \in T$
. In fact, since T is indecomposable,
![]() $d_{\lambda }$
is a metric on T. For the converse, let
$d_{\lambda }$
is a metric on T. For the converse, let
![]() $T' \in X_T$
. Then the pull back of Lebesgue measure on
$T' \in X_T$
. Then the pull back of Lebesgue measure on
![]() $T'$
under identity map
$T'$
under identity map
![]() $\operatorname {\mathrm {id}} \colon \, T \to T'$
gives a positive length measure on T.
$\operatorname {\mathrm {id}} \colon \, T \to T'$
gives a positive length measure on T.
We say T is uniquely ergometric if there is only one projective class of length measures on T, which necessarily is the homothety class of the Lebesgue measure on T. It is called nonuniquely ergometric otherwise.
2.5. Arational trees and the free factor complex
For a tree
![]() $T \in {\overline {\text {cv}}_{n}}$
and a free factor H of
$T \in {\overline {\text {cv}}_{n}}$
and a free factor H of
![]() ${\mathbb {F}_{n}}$
, let
${\mathbb {F}_{n}}$
, let
![]() $T_H$
denote the minimal H-invariant subtree of T (this tree is unique unless H fixes an arc). A tree
$T_H$
denote the minimal H-invariant subtree of T (this tree is unique unless H fixes an arc). A tree
![]() $T \in \partial {\text {cv}_{n}} $
is arational if every proper free factor H of
$T \in \partial {\text {cv}_{n}} $
is arational if every proper free factor H of
![]() ${\mathbb {F}_{n}}$
has a free and simplicial action on
${\mathbb {F}_{n}}$
has a free and simplicial action on
![]() $T_H$
. By [Reference ReynoldsRey12], every arational tree is free and indecomposable or it is the dual tree to an arational measured lamination on a surface with one puncture. The arational trees of the first kind are either Levitt type or nongeometric.
$T_H$
. By [Reference ReynoldsRey12], every arational tree is free and indecomposable or it is the dual tree to an arational measured lamination on a surface with one puncture. The arational trees of the first kind are either Levitt type or nongeometric.
Let
![]() $\mathcal {AT} \subset \partial {\text {CV}_{n}} $
denote the set of arational trees with the subspace topology. Using Lemma 2.3, define an equivalence relation
$\mathcal {AT} \subset \partial {\text {CV}_{n}} $
denote the set of arational trees with the subspace topology. Using Lemma 2.3, define an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $\mathcal {AT}$
by ‘forgetting the metric’, that is,
$\mathcal {AT}$
by ‘forgetting the metric’, that is,
![]() $T \sim T'$
if
$T \sim T'$
if
![]() $T' \in {\mathbb P} {\mathcal D}(T)$
, and endow
$T' \in {\mathbb P} {\mathcal D}(T)$
, and endow
![]() $\mathcal {AT}/\sim $
with the quotient topology. The following lemma is implicit in [Reference GuirardelGui00] and we include a proof for completeness.
$\mathcal {AT}/\sim $
with the quotient topology. The following lemma is implicit in [Reference GuirardelGui00] and we include a proof for completeness.
Lemma 2.4. Let
![]() $T, T'$
be arational trees. Then
$T, T'$
be arational trees. Then
![]() $T \sim T'$
if and only if
$T \sim T'$
if and only if
![]() $L(T) = L(T')$
.
$L(T) = L(T')$
.
Proof. If
![]() $T \sim T'$
, then the identity map
$T \sim T'$
, then the identity map
![]() $\operatorname {\mathrm {id}} \colon \, T \to T'$
is an alignment-preserving bijection. Therefore, by Theorem 2.2,
$\operatorname {\mathrm {id}} \colon \, T \to T'$
is an alignment-preserving bijection. Therefore, by Theorem 2.2,
![]() $L(T) = L(T')$
.
$L(T) = L(T')$
.
If
![]() $L(T) = L(T')$
, then by Theorem 2.2 there is an alignment preserving bijection
$L(T) = L(T')$
, then by Theorem 2.2 there is an alignment preserving bijection
![]() $f \colon \, T \to T'$
. Pulling back the Lebesgue measure on
$f \colon \, T \to T'$
. Pulling back the Lebesgue measure on
![]() $T'$
induces a length measure on T, and the corresponding metric
$T'$
induces a length measure on T, and the corresponding metric
![]() $d_\mu $
on T is isometric to
$d_\mu $
on T is isometric to
![]() $T'$
, so
$T'$
, so
![]() $T' \sim T$
.
$T' \sim T$
.
The free factor complex
![]() ${\mathcal {FF}_{n}}$
is a simplicial complex whose vertices are given by conjugacy classes of proper free factors of
${\mathcal {FF}_{n}}$
is a simplicial complex whose vertices are given by conjugacy classes of proper free factors of
![]() ${\mathbb {F}_{n}}$
and a k-simplex is given by a nested chain
${\mathbb {F}_{n}}$
and a k-simplex is given by a nested chain
![]() $[A_0] \subset [A_1] \subset \cdots \subset [A_k]$
. When the rank
$[A_0] \subset [A_1] \subset \cdots \subset [A_k]$
. When the rank
![]() $n=2$
the definition is modified and an edge connects two conjugacy classes of rank 1 factors if they have complementary representatives. The free factor complex can be given a metric as follows: Identify each simplex with a standard simplex and endow the resulting space with path metric. By result of [Reference Bestvina and FeighnBF14a], the metric space
$n=2$
the definition is modified and an edge connects two conjugacy classes of rank 1 factors if they have complementary representatives. The free factor complex can be given a metric as follows: Identify each simplex with a standard simplex and endow the resulting space with path metric. By result of [Reference Bestvina and FeighnBF14a], the metric space
![]() ${\mathcal {FF}_{n}}$
is Gromov hyperbolic. The Gromov boundary of
${\mathcal {FF}_{n}}$
is Gromov hyperbolic. The Gromov boundary of
![]() ${\mathcal {FF}_{n}}$
was identified with
${\mathcal {FF}_{n}}$
was identified with
![]() $\mathcal {AT}/\sim $
in [Reference Bestvina and ReynoldsBR15] and [Reference HamenstädtHam16].
$\mathcal {AT}/\sim $
in [Reference Bestvina and ReynoldsBR15] and [Reference HamenstädtHam16].
There is a projection map
![]() $\pi \colon \, {\text {CV}_{n}} \to {\mathcal {FF}_{n}}$
defined as follows [Reference Bestvina and FeighnBF14a, Section 3]: for
$\pi \colon \, {\text {CV}_{n}} \to {\mathcal {FF}_{n}}$
defined as follows [Reference Bestvina and FeighnBF14a, Section 3]: for
![]() $G \in {\text {CV}_{n}} $
,
$G \in {\text {CV}_{n}} $
,
![]() $\pi (G)$
is the collection of free factors given by the fundamental group of proper subgraphs of G which are not forests. This map is coarsely well defined, that is,
$\pi (G)$
is the collection of free factors given by the fundamental group of proper subgraphs of G which are not forests. This map is coarsely well defined, that is,
![]() $\operatorname {\mathrm {diam}}_{{\mathcal {FF}_{n}}}(\pi (G)) \le K$
for some universal K. Note that if
$\operatorname {\mathrm {diam}}_{{\mathcal {FF}_{n}}}(\pi (G)) \le K$
for some universal K. Note that if
![]() $G, G'$
belong to the same open simplex of
$G, G'$
belong to the same open simplex of
![]() ${\text {CV}_{n}} $
, then
${\text {CV}_{n}} $
, then
![]() $\pi (G)=\pi (G')$
, so the projection of a simplex of
$\pi (G)=\pi (G')$
, so the projection of a simplex of
![]() ${\text {CV}_{n}} $
has uniformly bounded diameter.
${\text {CV}_{n}} $
has uniformly bounded diameter.
3. Folding and unfolding sequences
In this section we introduce (un)folding sequences and review some work of Namazi-Pettet–Reynolds [Reference Namazi, Pettet and ReynoldsNPR14].
A folding/unfolding sequence is a sequence
of graphs, together with maps
![]() $f_i\colon \, G_i \to G_{i+1}$
such that for any
$f_i\colon \, G_i \to G_{i+1}$
such that for any
![]() $j \leq i$
,
$j \leq i$
,
![]() $f_{i-1} \circ f_{i-2} \circ \cdots \circ f_j\colon \, G_j \to G_i$
is a change-of-marking morphism. Equivalently, a sequence as above is called a folding/unfolding sequence, if there exists a train track structure on each
$f_{i-1} \circ f_{i-2} \circ \cdots \circ f_j\colon \, G_j \to G_i$
is a change-of-marking morphism. Equivalently, a sequence as above is called a folding/unfolding sequence, if there exists a train track structure on each
![]() $G_i$
and
$G_i$
and
![]() $f_{i-1} \circ f_{i-2} \circ \cdots \circ f_j$
maps legal paths to legal paths. We allow the sequence to be infinite in one or both directions. We assume that a marking on
$f_{i-1} \circ f_{i-2} \circ \cdots \circ f_j$
maps legal paths to legal paths. We allow the sequence to be infinite in one or both directions. We assume that a marking on
![]() $G_0$
has been specified, so a folding/unfolding sequence determines a sequence of open simplices in Outer space.
$G_0$
has been specified, so a folding/unfolding sequence determines a sequence of open simplices in Outer space.
Let
![]() $Q_i$
be the transition matrix of
$Q_i$
be the transition matrix of
![]() $f_{i}$
. A length measure for a folding/unfolding sequence
$f_{i}$
. A length measure for a folding/unfolding sequence
![]() $(G_i)_{a \leq i \leq b}$
is a sequence
$(G_i)_{a \leq i \leq b}$
is a sequence
![]() $(\lambda _i)_{a \leq i \leq b}$
, where
$(\lambda _i)_{a \leq i \leq b}$
, where
![]() $\lambda _i \in {\mathbb R}^{|EG_i|}$
is a length vector on
$\lambda _i \in {\mathbb R}^{|EG_i|}$
is a length vector on
![]() $G_i$
, and for
$G_i$
, and for
![]() $a \leq i < b$
,
$a \leq i < b$
,
In this way,
![]() $f_i$
restricts to a local isometry on every edge of
$f_i$
restricts to a local isometry on every edge of
![]() $G_i$
. When
$G_i$
. When
![]() $b < \infty $
, a length vector on
$b < \infty $
, a length vector on
![]() $G_b$
determines a length measure on the sequence. When the sequence is infinite in the forward direction we denote by
$G_b$
determines a length measure on the sequence. When the sequence is infinite in the forward direction we denote by
![]() ${\mathcal D}((G_i)_i)$
the space of length measures on
${\mathcal D}((G_i)_i)$
the space of length measures on
![]() $(G_i)_i$
, and
$(G_i)_i$
, and
![]() ${\mathbb P}{\mathcal D}((G_i)_i)$
its projectivization. Observe that the dimension of
${\mathbb P}{\mathcal D}((G_i)_i)$
its projectivization. Observe that the dimension of
![]() ${\mathcal D}((G_i)_i)$
is bounded by
${\mathcal D}((G_i)_i)$
is bounded by
![]() $\liminf _{i \to \infty }|EG_i|$
.
$\liminf _{i \to \infty }|EG_i|$
.
A current for a folding/unfolding sequence
![]() $(G_i)_{a \leq i \leq b}$
is a sequence
$(G_i)_{a \leq i \leq b}$
is a sequence
![]() $(\mu _i)_{a \leq i \leq b}$
, where
$(\mu _i)_{a \leq i \leq b}$
, where
![]() $\mu _i \in {\mathbb R}^{|EG_i|}$
is a length vector on
$\mu _i \in {\mathbb R}^{|EG_i|}$
is a length vector on
![]() $G_i$
(but thought of as a vector of thicknesses of edges), and for
$G_i$
(but thought of as a vector of thicknesses of edges), and for
![]() $a \leq i < b$
, we require
$a \leq i < b$
, we require
Likewise, when the sequence is infinite in the backward direction, we denote by
![]() $\text {Curr}((G_i)_i)$
the space of currents on
$\text {Curr}((G_i)_i)$
the space of currents on
![]() $(G_i)_i$
, and
$(G_i)_i$
, and
![]() ${\mathbb P}\text {Curr}((G_i)_i)$
its projectivization. The dimension of
${\mathbb P}\text {Curr}((G_i)_i)$
its projectivization. The dimension of
![]() $\text {Curr}((G_i)_i)$
is bounded by
$\text {Curr}((G_i)_i)$
is bounded by
![]() $\liminf _{i \to - \infty }|EG_i|$
.
$\liminf _{i \to - \infty }|EG_i|$
.
3.1. Isomorphism between length measures
In this section, we identify the space of length measures on a folding sequence with that of the limiting tree when it is an arational tree.
Consider a folding sequence of marked graphs of rank n

Let
![]() $\tilde G_i$
be the universal cover of
$\tilde G_i$
be the universal cover of
![]() $G_i$
, and let
$G_i$
, and let
![]() $\tilde f_i$
be a lift of
$\tilde f_i$
be a lift of
![]() $f_i$
. For any positive length measure
$f_i$
. For any positive length measure
![]() $(\lambda _i)_i \in {\mathcal D}((G_i)_i)$
, we can realize
$(\lambda _i)_i \in {\mathcal D}((G_i)_i)$
, we can realize
![]() $(\tilde G_i, \tilde \lambda _i)_i$
as a sequence in
$(\tilde G_i, \tilde \lambda _i)_i$
as a sequence in
![]() ${\text {cv}_{n}} $
, which can be ‘filled in’ by a folding path in
${\text {cv}_{n}} $
, which can be ‘filled in’ by a folding path in
![]() ${\text {cv}_{n}} $
(see [Reference Bestvina and FeighnBF14a] for details on folding paths). In particular,
${\text {cv}_{n}} $
(see [Reference Bestvina and FeighnBF14a] for details on folding paths). In particular,
![]() $(\tilde G_i,\tilde \lambda _i)_i$
always converges to a point
$(\tilde G_i,\tilde \lambda _i)_i$
always converges to a point
![]() $T \in \partial {\text {cv}_{n}} $
. Furthermore, we have morphisms
$T \in \partial {\text {cv}_{n}} $
. Furthermore, we have morphisms
![]() $h_i \colon \, \tilde G_i \to T$
such that
$h_i \colon \, \tilde G_i \to T$
such that
![]() $h_i = h_{i+1} \tilde f_{i+1}$
. With respect to the length measure
$h_i = h_{i+1} \tilde f_{i+1}$
. With respect to the length measure
![]() $\tilde \lambda _i$
,
$\tilde \lambda _i$
,
![]() $\tilde f_i$
and
$\tilde f_i$
and
![]() $h_i$
restrict to isometries on edges [Reference Bestvina and ReynoldsBR15, Lemma 7.6].
$h_i$
restrict to isometries on edges [Reference Bestvina and ReynoldsBR15, Lemma 7.6].
Let
![]() $(U_i)_i$
be the sequence of open simplices
$(U_i)_i$
be the sequence of open simplices
![]() ${\text {CV}_{n}} $
associated to the sequence
${\text {CV}_{n}} $
associated to the sequence
![]() $(G_i)_i$
. Recall the projection map
$(G_i)_i$
. Recall the projection map
![]() $\pi \colon \, {\text {CV}_{n}} \to {\mathcal {FF}_{n}}$
is coarsely well defined on simplices of
$\pi \colon \, {\text {CV}_{n}} \to {\mathcal {FF}_{n}}$
is coarsely well defined on simplices of
![]() ${\text {CV}_{n}} $
. We will say the folding sequence
${\text {CV}_{n}} $
. We will say the folding sequence
![]() $(G_i)_i$
converges to an arational tree T if
$(G_i)_i$
converges to an arational tree T if
![]() $\pi (U_i)$
converges to
$\pi (U_i)$
converges to
![]() $[T] \in \partial {\mathcal {FF}_{n}}$
.
$[T] \in \partial {\mathcal {FF}_{n}}$
.
Proposition 3.1. Suppose a folding sequence
![]() $(G_i)_i$
converges to an arational tree T. Then there is a linear isomorphism between
$(G_i)_i$
converges to an arational tree T. Then there is a linear isomorphism between
![]() ${\mathcal D}((G_i)_i)$
and
${\mathcal D}((G_i)_i)$
and
![]() ${\mathcal D}(T)$
.
${\mathcal D}(T)$
.
Proof. Fix a positive length measure
![]() $(\lambda _i)_i \in {\mathcal D}((G_i)_i)$
and let
$(\lambda _i)_i \in {\mathcal D}((G_i)_i)$
and let
![]() $T \in \partial {\text {cv}_{n}} $
be the limiting tree of
$T \in \partial {\text {cv}_{n}} $
be the limiting tree of
![]() $(\tilde G_i,\tilde \lambda _i)$
with corresponding morphism
$(\tilde G_i,\tilde \lambda _i)$
with corresponding morphism
![]() $h_i \colon \, \tilde G_i \to T$
. Recall from Section 2.5 that if T is arational, then we can identify
$h_i \colon \, \tilde G_i \to T$
. Recall from Section 2.5 that if T is arational, then we can identify
![]() ${\mathcal D}(T)$
with the subspace of
${\mathcal D}(T)$
with the subspace of
![]() ${\mathbb {F}_{n}}$
-metrics on T in
${\mathbb {F}_{n}}$
-metrics on T in
![]() $\partial {\text {cv}_{n}} $
. We will let
$\partial {\text {cv}_{n}} $
. We will let
![]() $\lambda \in {\mathcal D}(T)$
be a length measure, and
$\lambda \in {\mathcal D}(T)$
be a length measure, and
![]() $T_\lambda $
its image in
$T_\lambda $
its image in
![]() $\partial {\text {cv}_{n}} $
.
$\partial {\text {cv}_{n}} $
.
By [Reference Bestvina and ReynoldsBR15, Proposition 8.5], if
![]() $\pi (U_i)$
converges to
$\pi (U_i)$
converges to
![]() $[T"] \in \partial {\mathcal {FF}_{n}}$
, then for any positive
$[T"] \in \partial {\mathcal {FF}_{n}}$
, then for any positive
![]() $(\lambda _i')_i \in {\mathcal D}((G_i)_i)$
,
$(\lambda _i')_i \in {\mathcal D}((G_i)_i)$
,
![]() $(\tilde {G}_i,\tilde \lambda _i')$
also converges to an arational tree
$(\tilde {G}_i,\tilde \lambda _i')$
also converges to an arational tree
![]() $T' \in \partial {\text {cv}_{n}} $
, such that
$T' \in \partial {\text {cv}_{n}} $
, such that
![]() $[T"] = [T']=[T]$
; in other words,
$[T"] = [T']=[T]$
; in other words,
![]() $T' = T_{\lambda '}$
for some
$T' = T_{\lambda '}$
for some
![]() $\lambda ' \in D(T)$
. This gives a linear map
$\lambda ' \in D(T)$
. This gives a linear map
![]() ${\mathcal D}((G_i)_i) \to {\mathcal D}(T)$
.
${\mathcal D}((G_i)_i) \to {\mathcal D}(T)$
.
Conversely, for any positive length measure
![]() $\lambda ' \in {\mathcal D}(T)$
, we can use the morphism
$\lambda ' \in {\mathcal D}(T)$
, we can use the morphism
![]() $h_i$
to pull back
$h_i$
to pull back
![]() $\lambda '$
from T to a length measure
$\lambda '$
from T to a length measure
![]() $\lambda _i'$
on
$\lambda _i'$
on
![]() $\tilde {G}_i$
. The fact that
$\tilde {G}_i$
. The fact that
![]() $h_i = h_{i+1} \tilde f_{i+1}$
implies
$h_i = h_{i+1} \tilde f_{i+1}$
implies
![]() $(\lambda _i')_i \in {\mathcal D}((G_i)_i)$
. Moreover, the sequence
$(\lambda _i')_i \in {\mathcal D}((G_i)_i)$
. Moreover, the sequence
![]() $(\tilde {G}_i,\tilde \lambda _i')_i$
converges to
$(\tilde {G}_i,\tilde \lambda _i')_i$
converges to
![]() $T_{\lambda '} \in {\text {cv}_{n}} $
. This gives a linear map
$T_{\lambda '} \in {\text {cv}_{n}} $
. This gives a linear map
![]() ${\mathcal D}(T) \to {\mathcal D}((G_i)_i)$
which is the inverse of
${\mathcal D}(T) \to {\mathcal D}((G_i)_i)$
which is the inverse of
![]() ${\mathcal D}((G_i)_i) \to {\mathcal D}(T)$
defined above. This shows
${\mathcal D}((G_i)_i) \to {\mathcal D}(T)$
defined above. This shows
![]() ${\mathcal D}((G_i)_i) \to {\mathcal D}(T)$
is an isomorphism.
${\mathcal D}((G_i)_i) \to {\mathcal D}(T)$
is an isomorphism.
Remark 3.2. A more general statement of Proposition 3.1 which doesn’t involve the assumption that T is arational can be found in [Reference Namazi, Pettet and ReynoldsNPR14, Proposition 5.4], but we will not need such a general statement here.
3.2. Isomorphism between currents
In this section, we state an analogous result identifying the space of currents on an unfolding sequence with the space of currents of a legal lamination associated to a unfolding sequence. We record some definitions from [Reference Namazi, Pettet and ReynoldsNPR14] first.
Consider an unfolding sequence of marked graphs of rank n

Denote the composition
![]() $F_i = f_1 \circ \cdots \circ f_i$
. Let
$F_i = f_1 \circ \cdots \circ f_i$
. Let
![]() $\Omega ^L_{\infty }(G_i)$
denote the set of bi-infinite legal paths in
$\Omega ^L_{\infty }(G_i)$
denote the set of bi-infinite legal paths in
![]() $G_i$
. Define the legal lamination of the unfolding sequence
$G_i$
. Define the legal lamination of the unfolding sequence
![]() $(G_i)_i$
to be
$(G_i)_i$
to be
Use the marking on
![]() $G_0$
to identify
$G_0$
to identify
![]() $\partial ^2 \pi _1(G_0)$
with
$\partial ^2 \pi _1(G_0)$
with
![]() $\partial ^2 {\mathbb {F}_{n}}$
. The preimage, in
$\partial ^2 {\mathbb {F}_{n}}$
. The preimage, in
![]() $\partial ^2 {\mathbb {F}_{n}}$
, of the lift of
$\partial ^2 {\mathbb {F}_{n}}$
, of the lift of
![]() $\Lambda $
to
$\Lambda $
to
![]() $\partial ^2 \pi _1(G_0)$
is a lamination
$\partial ^2 \pi _1(G_0)$
is a lamination
![]() $\tilde {\Lambda }$
. We denote by
$\tilde {\Lambda }$
. We denote by
![]() $\text {Curr}(\Lambda )$
the convex cone of currents supported on
$\text {Curr}(\Lambda )$
the convex cone of currents supported on
![]() $\tilde {\Lambda }$
, with projectivization
$\tilde {\Lambda }$
, with projectivization
![]() ${\mathbb P}\text {Curr}(\Lambda )$
.
${\mathbb P}\text {Curr}(\Lambda )$
.
An invariant sequence of subgraphs is a sequence of nondegenerate (i.e., not forests) proper subgraphs
![]() $H_i \subset G_i$
such that
$H_i \subset G_i$
such that
![]() $f_i$
restricts to a morphism
$f_i$
restricts to a morphism
![]() $H_i \to H_{i-1}$
. We will need the following theorem from [Reference Namazi, Pettet and ReynoldsNPR14], which we will include a sketch of the proof for completeness.
$H_i \to H_{i-1}$
. We will need the following theorem from [Reference Namazi, Pettet and ReynoldsNPR14], which we will include a sketch of the proof for completeness.
Theorem 3.3 (Theorem 4.4 [Reference Namazi, Pettet and ReynoldsNPR14])
Given an unfolding sequence
![]() $(G_i)_{i \geq 0}$
without an invariant sequence of subgraphs and with legal lamination
$(G_i)_{i \geq 0}$
without an invariant sequence of subgraphs and with legal lamination
![]() $\Lambda $
, then there is a natural linear isomorphism between
$\Lambda $
, then there is a natural linear isomorphism between
![]() $\text {Curr}((G_i)_i)$
and
$\text {Curr}((G_i)_i)$
and
![]() $\text {Curr}(\Lambda )$
.
$\text {Curr}(\Lambda )$
.
Sketch of proof.
The lamination
![]() $\Lambda $
consists of biinfinite lines in
$\Lambda $
consists of biinfinite lines in
![]() $G_0$
that lift to every
$G_0$
that lift to every
![]() $G_i$
. All such lines are legal, and we view
$G_i$
. All such lines are legal, and we view
![]() $\Lambda $
as a subset of
$\Lambda $
as a subset of
![]() $(\partial \mathbb F)^2$
invariant under the involution that flips the factors. An element in
$(\partial \mathbb F)^2$
invariant under the involution that flips the factors. An element in
![]() $\text {Curr}((G_i)_i)$
is a compatible sequence
$\text {Curr}((G_i)_i)$
is a compatible sequence
![]() $(\mu _i)_i$
, where
$(\mu _i)_i$
, where
![]() $\mu _i$
assigns a nonnegative weight to each edge of
$\mu _i$
assigns a nonnegative weight to each edge of
![]() $G_i$
. The compatibility condition is that the transition matrix of
$G_i$
. The compatibility condition is that the transition matrix of
![]() $G_{i+1}\to G_i$
takes the vector
$G_{i+1}\to G_i$
takes the vector
![]() $\mu _{i+1}$
to the vector
$\mu _{i+1}$
to the vector
![]() $\mu _i$
. An alternative way to describe compatibility is this. Let
$\mu _i$
. An alternative way to describe compatibility is this. Let
![]() $\tilde G_i$
be the universal cover of
$\tilde G_i$
be the universal cover of
![]() $G_i$
, and let
$G_i$
, and let
![]() $F_{i+1}:\tilde G_{i+1}\to \tilde G_i$
be a lift of the folding map. The weights
$F_{i+1}:\tilde G_{i+1}\to \tilde G_i$
be a lift of the folding map. The weights
![]() $\mu _{i+1},\mu _i$
lift to the edges of
$\mu _{i+1},\mu _i$
lift to the edges of
![]() $\tilde G_{i+1},\tilde G_i$
. If e is an edge of
$\tilde G_{i+1},\tilde G_i$
. If e is an edge of
![]() $\tilde G_i$
, then
$\tilde G_i$
, then
![]() $F_{i+1}^{-1}(e)$
is a finite collection of partial edges in
$F_{i+1}^{-1}(e)$
is a finite collection of partial edges in
![]() $\tilde G_{i+1}$
, and we complete them to edges, say
$\tilde G_{i+1}$
, and we complete them to edges, say
![]() $e_1,e_2,\cdots ,e_k$
. The compatibility condition is
$e_1,e_2,\cdots ,e_k$
. The compatibility condition is
Since
![]() $F_{i+1}$
is injective on the leaves of
$F_{i+1}$
is injective on the leaves of
![]() $\Lambda $
, no such leaf passes through more than one of the
$\Lambda $
, no such leaf passes through more than one of the
![]() $e_j$
’s. Let
$e_j$
’s. Let
![]() $\text {Cyl}_{\Lambda }(e)$
be the set of leaves of
$\text {Cyl}_{\Lambda }(e)$
be the set of leaves of
![]() $\Lambda $
that pass through e and similarly for
$\Lambda $
that pass through e and similarly for
![]() $\text {Cyl}_\Lambda (e_j)$
. Thus, we have
$\text {Cyl}_\Lambda (e_j)$
. Thus, we have
Define measure
![]() $\mu $
on the cylinder sets corresponding to edges:
$\mu $
on the cylinder sets corresponding to edges:
The compatibility condition states that this measure is additive. The assumption that the sequence has no invariant subgraphs implies that cylinder sets corresponding to edges form a basis for the topology on
![]() $\Lambda $
. This allows us to extend
$\Lambda $
. This allows us to extend
![]() $\mu $
to general cylinder sets
$\mu $
to general cylinder sets
![]() $\text {Cyl}_{\Lambda }(\gamma )$
, where
$\text {Cyl}_{\Lambda }(\gamma )$
, where
![]() $\gamma $
is a finite segment of
$\gamma $
is a finite segment of
![]() $\Lambda $
in
$\Lambda $
in
![]() $\tilde {G}_i$
. The key is that folding cannot identify vertices in the same orbit. Thus, there is a uniform upper bound on the number of vertices that map to the same vertex for any
$\tilde {G}_i$
. The key is that folding cannot identify vertices in the same orbit. Thus, there is a uniform upper bound on the number of vertices that map to the same vertex for any
![]() $\tilde G_j\to \tilde G_i$
. When
$\tilde G_j\to \tilde G_i$
. When
![]() $\gamma $
is a segment, the preimages of
$\gamma $
is a segment, the preimages of
![]() $\gamma $
in
$\gamma $
in
![]() $\tilde G_j$
, for j sufficiently large, will be contained in either single edges or concatenations of two edges (see Lemma 8.2). By the above remark, the number of the length-2 paths is bounded by the combinatorial length of
$\tilde G_j$
, for j sufficiently large, will be contained in either single edges or concatenations of two edges (see Lemma 8.2). By the above remark, the number of the length-2 paths is bounded by the combinatorial length of
![]() $\gamma $
times the number of vertices in
$\gamma $
times the number of vertices in
![]() $G_j$
. While we don’t have enough information from
$G_j$
. While we don’t have enough information from
![]() $\mu _j$
alone to assign measure to these cylinder sets, we know their contribution goes to 0 as
$\mu _j$
alone to assign measure to these cylinder sets, we know their contribution goes to 0 as
![]() $j\to \infty $
. So for each j, we take the sum of the measures of cylinder sets of the single edges in the preimage of
$j\to \infty $
. So for each j, we take the sum of the measures of cylinder sets of the single edges in the preimage of
![]() $\gamma $
. This is an increasing and bounded sequence as
$\gamma $
. This is an increasing and bounded sequence as
![]() $j\to \infty $
, so we define
$j\to \infty $
, so we define
![]() $\mu (\text {Cyl}_\Lambda (\gamma ))$
to be the limit, and this is the only possible definition. It is now an exercise to check that
$\mu (\text {Cyl}_\Lambda (\gamma ))$
to be the limit, and this is the only possible definition. It is now an exercise to check that
![]() $\mu $
induces a premeasure on the semiring of cylinder sets
$\mu $
induces a premeasure on the semiring of cylinder sets
![]() $\text {Cyl}_{\Lambda }(\gamma )$
. Carathéodory’s theorem then implies that
$\text {Cyl}_{\Lambda }(\gamma )$
. Carathéodory’s theorem then implies that
![]() $\mu $
extends to a unique (Radon) measure on
$\mu $
extends to a unique (Radon) measure on
![]() $\Lambda $
, which finishes the proof.
$\Lambda $
, which finishes the proof.
4. Main setup
In this section, we will construct an unfolding sequence
![]() $(\tau _i)_i$
and a folding sequence
$(\tau _i)_i$
and a folding sequence
![]() $(\tau _i')_i$
in
$(\tau _i')_i$
in
![]() ${\text {CV}_{7}}$
that intersect the same infinite set of simplices, which we will eventually use to show the existence of a nonuniquely ergodic and ergometric tree. The construction is done via a family of outer automorphisms. We will describe these automorphisms and then analyze the asymptotic behavior of their train track maps.
${\text {CV}_{7}}$
that intersect the same infinite set of simplices, which we will eventually use to show the existence of a nonuniquely ergodic and ergometric tree. The construction is done via a family of outer automorphisms. We will describe these automorphisms and then analyze the asymptotic behavior of their train track maps.
4.1. The automorphisms
Let
![]() ${\mathbb {F}_{7}}=\langle a,b,c,d,e,f,g\rangle $
. Denote by
${\mathbb {F}_{7}}=\langle a,b,c,d,e,f,g\rangle $
. Denote by
![]() $\bar {x}$
the inverse of
$\bar {x}$
the inverse of
![]() $x \in {\mathbb {F}_{7}}$
. First, consider the map induced on the three-petaled rose by the automorphism
$x \in {\mathbb {F}_{7}}$
. First, consider the map induced on the three-petaled rose by the automorphism
and the map induced by the inverse automorphism
Using
![]() $\theta $
and
$\theta $
and
![]() $\vartheta $
to also denote the corresponding graph maps and using the convention that a also denotes the initial direction of the oriented edge a, while
$\vartheta $
to also denote the corresponding graph maps and using the convention that a also denotes the initial direction of the oriented edge a, while
![]() $\bar {a}$
denotes the terminal direction, we have the maps
$\bar {a}$
denotes the terminal direction, we have the maps
![]() $D\theta ^3$
and
$D\theta ^3$
and
![]() $D\vartheta ^3$
given, respectively, as:
$D\vartheta ^3$
given, respectively, as:
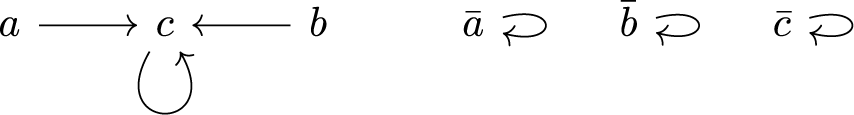
Observation 4.1. From the structure of the above maps, for
![]() $n\equiv 0$
mod 3,
$n\equiv 0$
mod 3,
![]() $D\theta ^n = D\theta ^3$
and
$D\theta ^n = D\theta ^3$
and
![]() $D\vartheta ^n = D\vartheta ^3$
.
$D\vartheta ^n = D\vartheta ^3$
.
Lemma 4.2. The map on the three-petaled rose labeled
![]() $a, b, c$
induced by
$a, b, c$
induced by
![]() $\vartheta $
is a train track map with respect to the train track structure with gates
$\vartheta $
is a train track map with respect to the train track structure with gates
![]() $\{a, \bar {c}\}, \{b, \bar {a}\}, \{c,\bar {b}\}$
. Moreover, this train track map does not have any periodic INPs.
$\{a, \bar {c}\}, \{b, \bar {a}\}, \{c,\bar {b}\}$
. Moreover, this train track map does not have any periodic INPs.
The map on the three-petaled rose labeled
![]() $a, b, c$
induced by
$a, b, c$
induced by
![]() $\theta $
is also a train track map with respect to the train track structure with gates
$\theta $
is also a train track map with respect to the train track structure with gates
![]() $\{a, b, c\}, \{\bar {a}\}, \{\bar {b}\}, \{\bar {c}\}$
and it has one periodic Nielsen path (see [Reference Bestvina and FeighnBF94, Example 3.4]).
$\{a, b, c\}, \{\bar {a}\}, \{\bar {b}\}, \{\bar {c}\}$
and it has one periodic Nielsen path (see [Reference Bestvina and FeighnBF94, Example 3.4]).
Proof. The train track structure on the rose induces a metric on the graph coming from Perron–Frobenius theory. Every INP has length at most twice the volume of the graph, one illegal turn and the endpoints are fixed. Since there are only finitely many fixed points in G, it is easy to enumerate all such paths and check if they are Nielsen. For periodic INPs one knows that the period is bounded by a function of the rank of
![]() ${\mathbb {F}_{n}}$
[Reference Feighn and HandelFH18], so one can take a suitable power and check for INPs (though there are more efficient ways, see [Reference KapovichKap19]). Coulbois’ train track package [Reference CoulboisCou] for the mathematics software system Sage [Reference DevelopersSag] computes periodic INPs of train track maps.
${\mathbb {F}_{n}}$
[Reference Feighn and HandelFH18], so one can take a suitable power and check for INPs (though there are more efficient ways, see [Reference KapovichKap19]). Coulbois’ train track package [Reference CoulboisCou] for the mathematics software system Sage [Reference DevelopersSag] computes periodic INPs of train track maps.
Now, let
![]() $\phi \in \operatorname {\mathrm {Aut}}({\mathbb {F}_{7}})$
be the automorphism:
$\phi \in \operatorname {\mathrm {Aut}}({\mathbb {F}_{7}})$
be the automorphism:
and
![]() $\rho \in \operatorname {\mathrm {Aut}}(\mathbb {F}_7)$
be the rotation by four clicks:
$\rho \in \operatorname {\mathrm {Aut}}(\mathbb {F}_7)$
be the rotation by four clicks:
Thus,
![]() $\phi $
is the extension of
$\phi $
is the extension of
![]() $\theta $
by identity, and
$\theta $
by identity, and
![]() $\rho $
rotates the support of
$\rho $
rotates the support of
![]() $\phi $
off itself.
$\phi $
off itself.
Lemma 4.3. For any
![]() $r \ge 3$
, the map on the seven-petaled rose induced by
$r \ge 3$
, the map on the seven-petaled rose induced by
![]() $\phi _r = \rho \phi ^r$
is a train track map with respect to the train track structure with gates
$\phi _r = \rho \phi ^r$
is a train track map with respect to the train track structure with gates
and eight more gates consisting of single half edges. The transition matrix
![]() $M_r$
has block form
$M_r$
has block form
 $$\begin{align*}\begin{pmatrix} 0&I\\ B^r&0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0&I\\ B^r&0 \end{pmatrix}, \end{align*}$$
where I is the
![]() $4\times 4$
identity matrix, and B is the transition matrix of
$4\times 4$
identity matrix, and B is the transition matrix of
![]() $\theta $
:
$\theta $
:
 $$\begin{align*}B= \begin{pmatrix} 0&0&1\\ 1&0&0\\ 0&1&1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}B= \begin{pmatrix} 0&0&1\\ 1&0&0\\ 0&1&1 \end{pmatrix}. \end{align*}$$
Proof. By Observation 4.1, we only have to check the lemma for
![]() $\phi _3, \phi _4, \phi _5$
, which can be done by hand or using the train track package for Sage.
$\phi _3, \phi _4, \phi _5$
, which can be done by hand or using the train track package for Sage.
Lemma 4.4. For any
![]() $r \ge 3$
and
$r \ge 3$
and
![]() $r \equiv 0$
mod 3, the map on the seven-petaled rose induced by
$r \equiv 0$
mod 3, the map on the seven-petaled rose induced by
![]() $\psi _r = (\rho \phi ^r)^{-1}$
is a train track map with respect to the train track structure with gates
$\psi _r = (\rho \phi ^r)^{-1}$
is a train track map with respect to the train track structure with gates
The transition matrix
![]() $N_r$
has block form
$N_r$
has block form
 $$\begin{align*}\begin{pmatrix} 0&C^r\\ I&0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0&C^r\\ I&0 \end{pmatrix}, \end{align*}$$
where I is the
![]() $4\times 4$
identity matrix, and C is the transition matrix of
$4\times 4$
identity matrix, and C is the transition matrix of
![]() $\vartheta $
:
$\vartheta $
:
 $$\begin{align*}C= \begin{pmatrix} 0&1&0\\ 1&0&1\\ 1&0&0 \end{pmatrix}. \end{align*}$$
$$\begin{align*}C= \begin{pmatrix} 0&1&0\\ 1&0&1\\ 1&0&0 \end{pmatrix}. \end{align*}$$
Proof. By Observation 4.1, we only have to check the lemma for
![]() $\psi _3$
, which can be done by hand or using the train track package for Sage.
$\psi _3$
, which can be done by hand or using the train track package for Sage.
4.2. Asymptotics of transition matrices
Let
![]() $\theta $
,
$\theta $
,
![]() $\vartheta $
,
$\vartheta $
,
![]() $\phi _r$
,
$\phi _r$
,
![]() $\psi _r$
be the maps defined in the last section. We now analyze the behavior of the transition matrices
$\psi _r$
be the maps defined in the last section. We now analyze the behavior of the transition matrices
![]() $M_r$
and
$M_r$
and
![]() $N_r$
for
$N_r$
for
![]() $\phi _r$
and
$\phi _r$
and
![]() $\psi _r$
, respectively.
$\psi _r$
, respectively.
Lemma 4.5. Let B be the transition matrix for
![]() $\theta $
, with Perron–Frobenius eigenvalue
$\theta $
, with Perron–Frobenius eigenvalue
![]() $\lambda _B$
. There exists a constant
$\lambda _B$
. There exists a constant
![]() $\kappa _B>0$
such that if
$\kappa _B>0$
such that if
![]() $r,s-r\to \infty $
, then
$r,s-r\to \infty $
, then
where Y is an idempotent matrix of the form
and
![]() $\begin {pmatrix} u_1,u_2,u_3\end {pmatrix}^T$
is a Perron–Frobenius eigenvector of B.
$\begin {pmatrix} u_1,u_2,u_3\end {pmatrix}^T$
is a Perron–Frobenius eigenvector of B.
Proof. There exists a Perron–Frobenius eigenvector
![]() $x=(x_1,x_2,x_3)^T$
for B and constants
$x=(x_1,x_2,x_3)^T$
for B and constants
![]() $p, q> 0$
such that
$p, q> 0$
such that
 $$\begin{align*}P = \lim_{s \to \infty} \frac{B^s}{\lambda_B^s} = \begin{pmatrix} x & px & qx \end{pmatrix}. \end{align*}$$
$$\begin{align*}P = \lim_{s \to \infty} \frac{B^s}{\lambda_B^s} = \begin{pmatrix} x & px & qx \end{pmatrix}. \end{align*}$$
We have

The square of the limiting matrix above has a nonzero block where P is of the form
and zero elsewhere, so we set
We have a similar statement for the matrices
![]() $N_r$
.
$N_r$
.
Lemma 4.6. Let C be the transition matrix for
![]() $\vartheta = \theta ^{-1}$
, with Perron–Frobenius eigenvalue
$\vartheta = \theta ^{-1}$
, with Perron–Frobenius eigenvalue
![]() $\lambda _C$
. There exists a constant
$\lambda _C$
. There exists a constant
![]() $\kappa _C>0$
such that if
$\kappa _C>0$
such that if
![]() $r, s-r\to \infty $
, then
$r, s-r\to \infty $
, then
 $$ \begin{align*}\frac 1{\kappa_C \lambda_C^s} N_s N_r \to Z,\end{align*} $$
$$ \begin{align*}\frac 1{\kappa_C \lambda_C^s} N_s N_r \to Z,\end{align*} $$
where Z is an idempotent matrix of the form
and
![]() $(v_1,v_2,v_3)^T$
is a Perron–Frobenius eigenvector of C.
$(v_1,v_2,v_3)^T$
is a Perron–Frobenius eigenvector of C.
Proof. We observe that the matrix
![]() $N_s N_r$
has shape that is the transpose of the matrix in Lemma 4.5, with powers of the PF matrix C forming the nonzero blocks:
$N_s N_r$
has shape that is the transpose of the matrix in Lemma 4.5, with powers of the PF matrix C forming the nonzero blocks:
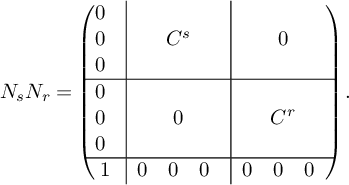
For future reference, we also record the following. Let
![]() $P = \lim _{r \to \infty } B^r/\lambda _B^r$
and
$P = \lim _{r \to \infty } B^r/\lambda _B^r$
and
![]() ${Q = \lim _{r \to \infty } C^r/\lambda _C^r}$
. Set
${Q = \lim _{r \to \infty } C^r/\lambda _C^r}$
. Set
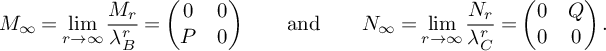 $$\begin{align*}M_\infty = \lim_{r \to \infty} \frac{M_r}{\lambda^r_B} =\begin{pmatrix} 0 & 0\\ P & 0 \end{pmatrix} \qquad \text{and} \qquad N_\infty = \lim_{r \to \infty} \frac{N_r}{\lambda^r_C} =\begin{pmatrix} 0 & Q \\ 0 & 0 \end{pmatrix}. \end{align*}$$
$$\begin{align*}M_\infty = \lim_{r \to \infty} \frac{M_r}{\lambda^r_B} =\begin{pmatrix} 0 & 0\\ P & 0 \end{pmatrix} \qquad \text{and} \qquad N_\infty = \lim_{r \to \infty} \frac{N_r}{\lambda^r_C} =\begin{pmatrix} 0 & Q \\ 0 & 0 \end{pmatrix}. \end{align*}$$
Lemma 4.7. There are
![]() $p,q,r,s> 0$
such that
$p,q,r,s> 0$
such that
![]() $(y_1,y_2,y_3)^T$
is a Perron–Frobenius eigenvector of B, and
$(y_1,y_2,y_3)^T$
is a Perron–Frobenius eigenvector of B, and
and
![]() $(z_1,z_2,z_3)^T$
is a Perron–Frobenius eigenvector of C.
$(z_1,z_2,z_3)^T$
is a Perron–Frobenius eigenvector of C.
4.3. Folding and unfolding sequence
Consider a sequence of positive integers
![]() $(r_i)_{i \ge 1}$
and the sequence of automorphisms
$(r_i)_{i \ge 1}$
and the sequence of automorphisms
![]() $\phi _{r_i}$
, with transition matrix
$\phi _{r_i}$
, with transition matrix
![]() $M_{r_i}$
and
$M_{r_i}$
and
![]() $\phi _{r_i}^{-1} = \psi _{r_i}$
with transition matrix
$\phi _{r_i}^{-1} = \psi _{r_i}$
with transition matrix
![]() $N_{r_i}$
. Let
$N_{r_i}$
. Let
![]() $\tau _i \to \tau _{i-1}$
(resp.
$\tau _i \to \tau _{i-1}$
(resp.
![]() $\tau _{i-1}' \to \tau _i'$
) be the train track map induced on the rose by
$\tau _{i-1}' \to \tau _i'$
) be the train track map induced on the rose by
![]() $\phi _{r_i}$
(resp.
$\phi _{r_i}$
(resp.
![]() $\psi _{r_i}$
) as given by Lemma 4.3 (resp. Lemma 4.4). Thus, we have an unfolding sequence
$\psi _{r_i}$
) as given by Lemma 4.3 (resp. Lemma 4.4). Thus, we have an unfolding sequence

and a folding sequence

Let
![]() $\Phi _i = \phi _{r_1} \circ \ldots \circ \phi _{r_i}$
and
$\Phi _i = \phi _{r_1} \circ \ldots \circ \phi _{r_i}$
and
![]() $\Phi _i^{-1} = \Psi _i = \psi _{r_i} \circ \ldots \circ \psi _{r_1}$
. Here,
$\Phi _i^{-1} = \Psi _i = \psi _{r_i} \circ \ldots \circ \psi _{r_1}$
. Here,
![]() $\tau _0$
is a rose with petals labeled by elements in
$\tau _0$
is a rose with petals labeled by elements in
![]() $\{a,b,c,d,e,f,g\}$
and hence for
$\{a,b,c,d,e,f,g\}$
and hence for
![]() $i \ge 1$
,
$i \ge 1$
,
![]() $\tau _i$
is a rose labeled by
$\tau _i$
is a rose labeled by
![]() $\{\Phi _i(a), \ldots , \Phi _i(g)\}$
. Also,
$\{\Phi _i(a), \ldots , \Phi _i(g)\}$
. Also,
![]() $\tau _0'$
is a rose labeled by
$\tau _0'$
is a rose labeled by
![]() $\{a,b,c,d,e,f,g\}$
, so
$\{a,b,c,d,e,f,g\}$
, so
![]() $\tau _i'$
is also a rose labeled by
$\tau _i'$
is also a rose labeled by
![]() $\{\Phi _i(a), \ldots , \Phi _i(g)\}$
. Thus, for every
$\{\Phi _i(a), \ldots , \Phi _i(g)\}$
. Thus, for every
![]() $i\geq 0$
,
$i\geq 0$
,
![]() $\tau _i$
and
$\tau _i$
and
![]() $\tau _i'$
have the same marking but different train track structures. In other words, they belong to the same simplex in
$\tau _i'$
have the same marking but different train track structures. In other words, they belong to the same simplex in
![]() ${\text {CV}_{7}}$
.
${\text {CV}_{7}}$
.
The next lemma studies the behavior of illegal turns in a path along the folding sequence. This will be used in the proof of Proposition 5.10 to show that the limit tree of the folding sequence is nongeometric.
Lemma 4.8. Let
![]() $(r_i)_{i \ge 1}$
be strictly increasing such that
$(r_i)_{i \ge 1}$
be strictly increasing such that
![]() $r_i \equiv 0$
mod 3 and
$r_i \equiv 0$
mod 3 and
![]() $r_1> R$
, where R is the constant from Lemma 2.1. Let
$r_1> R$
, where R is the constant from Lemma 2.1. Let
![]() $(\tau _i')_i$
be the corresponding folding sequence. Then for any edge path
$(\tau _i')_i$
be the corresponding folding sequence. Then for any edge path
![]() $\beta $
in
$\beta $
in
![]() $\tau ^{\prime }_j$
with at least one illegal turn, the number of illegal turns in
$\tau ^{\prime }_j$
with at least one illegal turn, the number of illegal turns in
![]() $[\psi _{r_{j+3}}\psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )]$
is less than the number of illegal turns in
$[\psi _{r_{j+3}}\psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )]$
is less than the number of illegal turns in
![]() $\beta $
.
$\beta $
.
Proof. By Lemma 4.4, the illegal turns in
![]() $\tau ^{\prime }_{j}$
are
$\tau ^{\prime }_{j}$
are
and we have
 $$\begin{align*}\{a,e\} & \xrightarrow{\psi_{r_{j+1}}} \{d,\bar{c}\} \xrightarrow{\psi_{r_{j+2}}} \{g,\bar{f}\} \\[2pt] \{a,\bar{g}\} & \xrightarrow{\psi_{r_{j+1}}} \{d,\bar{c}\} \xrightarrow{\psi_{r_{j+2}}} \{g,\bar{f}\} \\[2pt] \{b,\bar{d}\} & \xrightarrow{\psi_{r_{j+1}}} \{e,\bar{g}\} \\[2pt] \{c,\bar{b}\} & \xrightarrow{\psi_{r_{j+1}}} \{f,\bar{e}\} \\[2pt] \{d,\bar{c}\} & \xrightarrow{\psi_{r_{j+1}}} \{g,\bar{f}\}. \end{align*}$$
$$\begin{align*}\{a,e\} & \xrightarrow{\psi_{r_{j+1}}} \{d,\bar{c}\} \xrightarrow{\psi_{r_{j+2}}} \{g,\bar{f}\} \\[2pt] \{a,\bar{g}\} & \xrightarrow{\psi_{r_{j+1}}} \{d,\bar{c}\} \xrightarrow{\psi_{r_{j+2}}} \{g,\bar{f}\} \\[2pt] \{b,\bar{d}\} & \xrightarrow{\psi_{r_{j+1}}} \{e,\bar{g}\} \\[2pt] \{c,\bar{b}\} & \xrightarrow{\psi_{r_{j+1}}} \{f,\bar{e}\} \\[2pt] \{d,\bar{c}\} & \xrightarrow{\psi_{r_{j+1}}} \{g,\bar{f}\}. \end{align*}$$
Thus, for any illegal edge path
![]() $\beta \subset \tau _{j}'$
, one of
$\beta \subset \tau _{j}'$
, one of
![]() $\beta , \psi _{r_{j+1}}(\beta ), \psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )$
has an illegal turn
$\beta , \psi _{r_{j+1}}(\beta ), \psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )$
has an illegal turn
![]() $\{x, y\}$
, where
$\{x, y\}$
, where
![]() $x, y \in \{e, f, g, \bar {e}, \bar {f}, \bar {g}\}$
.
$x, y \in \{e, f, g, \bar {e}, \bar {f}, \bar {g}\}$
.
Consider the automorphism
![]() $\vartheta $
and corresponding train track map
$\vartheta $
and corresponding train track map
![]() $h \colon \, \mathrm {R}_3 \to \mathrm {R}_3$
as in Lemma 4.2. Then h does not have any periodic INPs. Since R is the constant from Lemma 2.1, we get that one of
$h \colon \, \mathrm {R}_3 \to \mathrm {R}_3$
as in Lemma 4.2. Then h does not have any periodic INPs. Since R is the constant from Lemma 2.1, we get that one of
![]() $[\psi _{r_{j+1}}(\beta )], [\psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )], [\psi _{r_{j+3}}\psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )]$
has fewer illegal turns than
$[\psi _{r_{j+1}}(\beta )], [\psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )], [\psi _{r_{j+3}}\psi _{r_{j+2}}\psi _{r_{j+1}}(\beta )]$
has fewer illegal turns than
![]() $\beta $
.
$\beta $
.
5. Limiting tree of folding sequence
In this section, we will show that for appropriate choices of
![]() $(r_i)_i$
, the projection of the folding sequences
$(r_i)_i$
, the projection of the folding sequences
![]() $(\tau _i')_i$
to the free factor complex
$(\tau _i')_i$
to the free factor complex
![]() ${\mathcal {FF}_{7}}$
is a quasi-geodesic and hence converges to the equivalence class of an arational tree. We will also show that this tree is nongeometric.
${\mathcal {FF}_{7}}$
is a quasi-geodesic and hence converges to the equivalence class of an arational tree. We will also show that this tree is nongeometric.
5.1. Sequence of free factors
Given a sequence
![]() $(r_i)_{i \ge 1}$
, recall that
$(r_i)_{i \ge 1}$
, recall that
![]() $\Phi _i = \phi _{r_1}\phi _{r_1}\cdots \phi _{r_i}$
, where
$\Phi _i = \phi _{r_1}\phi _{r_1}\cdots \phi _{r_i}$
, where
![]() $\phi _r = \rho \phi ^r$
. For convenience, also set
$\phi _r = \rho \phi ^r$
. For convenience, also set
![]() $\Phi _0 = \operatorname {\mathrm {id}}$
. We have the folding sequence
$\Phi _0 = \operatorname {\mathrm {id}}$
. We have the folding sequence

where
![]() $\tau _i'$
is a rose labeled by
$\tau _i'$
is a rose labeled by
![]() $\{ \Phi _i(a),\cdots ,\Phi _i(g)\}$
, and
$\{ \Phi _i(a),\cdots ,\Phi _i(g)\}$
, and
![]() $\psi _r = \phi _r^{-1}$
. From the markings, we can associate
$\psi _r = \phi _r^{-1}$
. From the markings, we can associate
![]() $\tau _i'$
to an open simplex
$\tau _i'$
to an open simplex
![]() $U_i$
in
$U_i$
in
![]() ${\text {CV}_{7}}$
. Consider a sequence of free factors
${\text {CV}_{7}}$
. Consider a sequence of free factors
![]() $A_i \in \pi (U_i)$
, where
$A_i \in \pi (U_i)$
, where
![]() $\pi \colon \, {\text {CV}_{7}} \to {\mathcal {FF}_{7}}$
. For an appropriate sequence of
$\pi \colon \, {\text {CV}_{7}} \to {\mathcal {FF}_{7}}$
. For an appropriate sequence of
![]() $(r_i)_i$
, we will see that
$(r_i)_i$
, we will see that
![]() $(A_i)_i$
is a quasi-geodesic (with infinite diameter). The key will be Lemma 5.3 which is the main goal of this section.
$(A_i)_i$
is a quasi-geodesic (with infinite diameter). The key will be Lemma 5.3 which is the main goal of this section.
We now consider the following explicit sequence of free factors. Let
![]() $A_0 = \langle d,e,f\rangle $
be the free factor in
$A_0 = \langle d,e,f\rangle $
be the free factor in
![]() ${\mathbb {F}_{7}}$
, and define
${\mathbb {F}_{7}}$
, and define
Note that for any
![]() $r,s,t>0$
, the following holds:
$r,s,t>0$
, the following holds:
 $$ \begin{align} \begin{aligned} A_0 &= \langle d, e, f \rangle \\ A_1 &= \phi_r(A_0) = \langle a, b, c \rangle \\ A_2 &= \phi_s\phi_r(A_0) = \langle e, f, g \rangle \\ A_3 &= \phi_t\phi_s\phi_r(A_0) = \langle b,c,d \rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} A_0 &= \langle d, e, f \rangle \\ A_1 &= \phi_r(A_0) = \langle a, b, c \rangle \\ A_2 &= \phi_s\phi_r(A_0) = \langle e, f, g \rangle \\ A_3 &= \phi_t\phi_s\phi_r(A_0) = \langle b,c,d \rangle. \end{aligned} \end{align} $$
Thus, for any sequence
![]() $(r_i)_i$
,
$(r_i)_i$
,
We say two free factors A and
![]() $A'$
are disjoint if (possibly after conjugating)
$A'$
are disjoint if (possibly after conjugating)
![]() ${\mathbb {F}_{n}}=A*A'*B$
for a (possibly trivial) free factor B, and
${\mathbb {F}_{n}}=A*A'*B$
for a (possibly trivial) free factor B, and
![]() $A'$
is compatible with A if it either contains A (up to conjugation) or is disjoint from A.
$A'$
is compatible with A if it either contains A (up to conjugation) or is disjoint from A.
Lemma 5.1. For any sequence
![]() $(r_i)_{i \ge 1}$
, if
$(r_i)_{i \ge 1}$
, if
![]() $|i-j|=1$
, then
$|i-j|=1$
, then
![]() $A_i, A_j$
are disjoint, and if
$A_i, A_j$
are disjoint, and if
![]() $|i-j| = 2$
or
$|i-j| = 2$
or
![]() $3$
, then they are distinct and not disjoint.
$3$
, then they are distinct and not disjoint.
Proof. We see from Equation 1 that the statement of the lemma holds for
![]() $A_0, A_1, A_2$
and
$A_0, A_1, A_2$
and
![]() $A_3$
. Now, for
$A_3$
. Now, for
![]() $i \ge 1$
and
$i \ge 1$
and
![]() $k \in \{1,2,3\}$
, by Equation 2, the pair
$k \in \{1,2,3\}$
, by Equation 2, the pair
![]() $A_i, A_{i+k}$
differs from
$A_i, A_{i+k}$
differs from
![]() $A_0, A_k$
by the automorphism
$A_0, A_k$
by the automorphism
![]() $\Phi _i$
, whence the lemma.
$\Phi _i$
, whence the lemma.
Recall the transition matrix
![]() $M_r$
for
$M_r$
for
![]() $\phi _r$
, and the
$\phi _r$
, and the
![]() $3\times 3$
matrix B whose power
$3\times 3$
matrix B whose power
![]() $B^r$
forms a block of
$B^r$
forms a block of
![]() $M_r$
. For each
$M_r$
. For each
![]() $i \ge 1$
, let
$i \ge 1$
, let
![]() $\overline {M}_i = M_i$
mod 2. By a simple computation, we see that
$\overline {M}_i = M_i$
mod 2. By a simple computation, we see that
![]() $B^7 = I$
mod 2. Thus, when
$B^7 = I$
mod 2. Thus, when
![]() $i = j$
mod 7,
$i = j$
mod 7,
![]() $\overline {M}_i = \overline {M}_j$
. We have the following lemma.
$\overline {M}_i = \overline {M}_j$
. We have the following lemma.
Lemma 5.2. Let
![]() $V_0$
be the three-dimensional vector space of
$V_0$
be the three-dimensional vector space of
![]() $(\mathbb {Z}/2\mathbb {Z})^7$
spanned by the vectors
$(\mathbb {Z}/2\mathbb {Z})^7$
spanned by the vectors
![]() $(0,0,0,1,0,0,0)^T,(0,0,0,0,1,0,0)^T,(0,0,0,0,0,1,0)^T$
. Then for all
$(0,0,0,1,0,0,0)^T,(0,0,0,0,1,0,0)^T,(0,0,0,0,0,1,0)^T$
. Then for all
![]() $i \ge 0$
,
$i \ge 0$
,
 $$\begin{align*}V_0 \bigcup \left( \bigcup_{j=0}^{107} \overline{M}_i \overline{M}_{i+1}\ldots \overline{M}_{i+j} V_0 \right) = (\mathbb{Z}/2\mathbb{Z})^7. \end{align*}$$
$$\begin{align*}V_0 \bigcup \left( \bigcup_{j=0}^{107} \overline{M}_i \overline{M}_{i+1}\ldots \overline{M}_{i+j} V_0 \right) = (\mathbb{Z}/2\mathbb{Z})^7. \end{align*}$$
Proof. Since
![]() $\overline {M}_i=\overline {M}_j$
whenever
$\overline {M}_i=\overline {M}_j$
whenever
![]() $i = j$
mod 7, it is enough to verify the statement for
$i = j$
mod 7, it is enough to verify the statement for
![]() $i \in \{0,\ldots ,6\}$
. In these cases, we can check the validity of the statement using Sage with the following code:
$i \in \{0,\ldots ,6\}$
. In these cases, we can check the validity of the statement using Sage with the following code:

Lemma 5.3. For any sequence
![]() $(r_i)_i$
, if
$(r_i)_i$
, if
![]() $r_i \equiv i \quad\mod 7$
, then
$r_i \equiv i \quad\mod 7$
, then
![]() $109$
consecutive
$109$
consecutive
![]() $A_i$
’s cannot be contained in the same free factor or be disjoint from a common factor.
$A_i$
’s cannot be contained in the same free factor or be disjoint from a common factor.
Proof. For any
![]() $i \ge 1$
and
$i \ge 1$
and
![]() $k \ge 0$
, let
$k \ge 0$
, let
Abelianizing and reducing mod 2, we have
![]() $A_0 \equiv V_0$
, and
$A_0 \equiv V_0$
, and
![]() $B_{i+k} \equiv \overline {M}_i \cdots \overline {M}_{i+k} V_0$
. Thus, by Lemma 5.2, the sequence
$B_{i+k} \equiv \overline {M}_i \cdots \overline {M}_{i+k} V_0$
. Thus, by Lemma 5.2, the sequence
![]() $\{A_0, B_i, \ldots , B_{i+107}\}$
cannot be contained in the same free factor or be disjoint from a common factor.
$\{A_0, B_i, \ldots , B_{i+107}\}$
cannot be contained in the same free factor or be disjoint from a common factor.
Now, consider any sequence
![]() $(r_i)_i$
with
$(r_i)_i$
with
![]() $r_i \equiv i$
mod
$r_i \equiv i$
mod
![]() $7$
so that
$7$
so that
![]() $\overline {M}_{r_i} = \overline {M}_i$
for all i. Let
$\overline {M}_{r_i} = \overline {M}_i$
for all i. Let
![]() $A_i = \Phi _i A_0 = \phi _{r_1} \cdots \phi _{r_i}A_0$
. Set
$A_i = \Phi _i A_0 = \phi _{r_1} \cdots \phi _{r_i}A_0$
. Set
![]() $\Phi _0 = \operatorname {\mathrm {id}}$
. For any
$\Phi _0 = \operatorname {\mathrm {id}}$
. For any
![]() $i \ge 1$
, by applying the automorphism
$i \ge 1$
, by applying the automorphism
![]() $\Phi _{i-1}^{-1}$
, the sequence of free factors
$\Phi _{i-1}^{-1}$
, the sequence of free factors
![]() $\{A_{i-1},\ldots ,A_{i+107}\}$
is isomorphic to the sequence
$\{A_{i-1},\ldots ,A_{i+107}\}$
is isomorphic to the sequence
The latter sequence after abelianization and reducing mod 2 is equivalent to the sequence
![]() $\{A_0,B_i,\ldots ,B_{i+107}\}$
. Thus,
$\{A_0,B_i,\ldots ,B_{i+107}\}$
. Thus,
![]() $\{A_{i-1},\ldots ,A_{i+107}\}$
cannot be contained in the same factor or be disjoint from a common factor.here
$\{A_{i-1},\ldots ,A_{i+107}\}$
cannot be contained in the same factor or be disjoint from a common factor.here
5.2. Subfactor projection
We will now use subfactor projection theory originally introduced in [Reference Bestvina and FeighnBF14b] and further developed in [Reference TaylorTay14] to show that
![]() $(A_i)_i$
is a quasi-geodesic for appropriate choices of sequence
$(A_i)_i$
is a quasi-geodesic for appropriate choices of sequence
![]() $(r_i)_i$
.
$(r_i)_i$
.
We first define subfactor projection and recall the main results about them. For
![]() $G \in {\text {CV}_{n}} $
and a rank
$G \in {\text {CV}_{n}} $
and a rank
![]() $\geq 2$
free factor A, let
$\geq 2$
free factor A, let
![]() $A|G$
denote the core subgraph of the cover of G corresponding to the conjugacy class of A. Pulling back the metric on G, we obtain
$A|G$
denote the core subgraph of the cover of G corresponding to the conjugacy class of A. Pulling back the metric on G, we obtain
![]() $A|G \in \mathrm {CV}(A)$
. Denote by
$A|G \in \mathrm {CV}(A)$
. Denote by
![]() $\pi _A(G):= \pi (A|G) \subset {\mathcal F}(A)$
the projection of
$\pi _A(G):= \pi (A|G) \subset {\mathcal F}(A)$
the projection of
![]() $A|G$
to
$A|G$
to
![]() ${\mathcal F}(A)$
. Here,
${\mathcal F}(A)$
. Here,
![]() $\mathrm {CV}(A)$
is the Outer space of the free group A and
$\mathrm {CV}(A)$
is the Outer space of the free group A and
![]() ${\mathcal F}(A)$
is the corresponding free factor complex.
${\mathcal F}(A)$
is the corresponding free factor complex.
Recall two free factors A and B are disjoint if they are distinct vertex stabilizers of a free splitting of
![]() ${\mathbb {F}_{n}}$
. If B is not compatible with A, then we say B meets A, that is, B and A are not disjoint and A is not contained in B, up to conjugation. In this case, define the projection of B to
${\mathbb {F}_{n}}$
. If B is not compatible with A, then we say B meets A, that is, B and A are not disjoint and A is not contained in B, up to conjugation. In this case, define the projection of B to
![]() ${\mathcal F}(A)$
as follows:
${\mathcal F}(A)$
as follows:
If B is compatible with A, then define
![]() $\pi _A(B)$
to be empty. If A meets B and B meets A, then we say A and B overlap.
$\pi _A(B)$
to be empty. If A meets B and B meets A, then we say A and B overlap.
Theorem 5.4 [Reference TaylorTay14]
Let
![]() $A,B,C$
be free factors of
$A,B,C$
be free factors of
![]() ${\mathbb {F}_{n}}$
. There is a constant D depending only on n such that the following statements hold.
${\mathbb {F}_{n}}$
. There is a constant D depending only on n such that the following statements hold.
-
1. If
 $\operatorname {\mathrm {rank}}(A) \ge 2$
, then either
$\operatorname {\mathrm {rank}}(A) \ge 2$
, then either
 $A \subseteq B$
(up to conjugation), A and B are disjoint, or
$A \subseteq B$
(up to conjugation), A and B are disjoint, or
 $\pi _A(B) \subset \mathcal {F}(A)$
is defined and has diameter
$\pi _A(B) \subset \mathcal {F}(A)$
is defined and has diameter
 $\leq D$
.
$\leq D$
. -
2. If
 $\operatorname {\mathrm {rank}}(A) \ge 2$
, B and C meet A and B is compatible with C, then
$\operatorname {\mathrm {rank}}(A) \ge 2$
, B and C meet A and B is compatible with C, then  $$\begin{align*}d_A(B,C) = \operatorname{\mathrm{diam}}_{{\mathcal F}(A)}(\pi_A(B) \cup \pi_A(C)) \le D.\end{align*}$$
$$\begin{align*}d_A(B,C) = \operatorname{\mathrm{diam}}_{{\mathcal F}(A)}(\pi_A(B) \cup \pi_A(C)) \le D.\end{align*}$$
-
3. If A and B overlap, have rank at least
 $2$
and C meets both, then
$2$
and C meets both, then  $$\begin{align*}\min \{ d_A(B,C), d_B(A,C)\} \le D.\end{align*}$$
$$\begin{align*}\min \{ d_A(B,C), d_B(A,C)\} \le D.\end{align*}$$
Theorem 5.5 (Bounded geodesic image theorem [Reference TaylorTay14])
For
![]() $n \geq 3$
, there exists
$n \geq 3$
, there exists
![]() $D' \geq 0$
such that if A is a free factor with
$D' \geq 0$
such that if A is a free factor with
![]() $\text {rank}(A) \geq 2$
and
$\text {rank}(A) \geq 2$
and
![]() $\gamma $
is a geodesic of
$\gamma $
is a geodesic of
![]() ${\mathcal {FF}_{n}}$
with each vertex of
${\mathcal {FF}_{n}}$
with each vertex of
![]() $\gamma $
having a well-defined projection to
$\gamma $
having a well-defined projection to
![]() ${\mathcal F}(A)$
, then
${\mathcal F}(A)$
, then
![]() $\text {diam}(\pi _A(\gamma )) \leq D'$
.
$\text {diam}(\pi _A(\gamma )) \leq D'$
.
We now prove the following lemma.
Lemma 5.6. For any
![]() $K>0$
, there exists a constant
$K>0$
, there exists a constant
![]() $r = r(K)$
such that for any sequence
$r = r(K)$
such that for any sequence
![]() $(r_i)_{i \ge 1}$
, if
$(r_i)_{i \ge 1}$
, if
![]() $r_i \ge r$
for all i, then the following statements hold:
$r_i \ge r$
for all i, then the following statements hold:
-
1. For any
 $j \geq 2$
, the projections of
$j \geq 2$
, the projections of
 $A_{j-2}$
and
$A_{j-2}$
and
 $A_{j+2}$
to the free factor complex
$A_{j+2}$
to the free factor complex
 ${\mathcal F}(A_j)$
are defined and the distance between them is at least K.
${\mathcal F}(A_j)$
are defined and the distance between them is at least K. -
2. Let D be the constant of Theorem 5.4. If
 $K> 3D,$
then for any
$K> 3D,$
then for any
 $i < j <k$
, if
$i < j <k$
, if
 $j-i\geq 2$
and
$j-i\geq 2$
and
 $k-j\geq 2$
, the projections of
$k-j\geq 2$
, the projections of
 $A_i$
and
$A_i$
and
 $A_k$
to
$A_k$
to
 ${\mathcal F}(A_j)$
are defined and have distance at least
${\mathcal F}(A_j)$
are defined and have distance at least
 $K-2D$
.
$K-2D$
.
Proof. Recall for any r,
![]() $\phi _r = \rho \phi ^r$
, where
$\phi _r = \rho \phi ^r$
, where
![]() $\phi $
restricts to a fully irreducible outer automorphism of
$\phi $
restricts to a fully irreducible outer automorphism of
![]() $\langle a, b, c\rangle $
. In particular,
$\langle a, b, c\rangle $
. In particular,
![]() $\phi $
acts as a loxodromic isometry of the free factor complex
$\phi $
acts as a loxodromic isometry of the free factor complex
![]() ${\mathcal F}(\langle a,b,c \rangle )$
, Thus, for any K, there exists
${\mathcal F}(\langle a,b,c \rangle )$
, Thus, for any K, there exists
![]() $r=r(K)$
such that for all
$r=r(K)$
such that for all
![]() $s \ge r$
, the distance between
$s \ge r$
, the distance between
![]() $\phi ^s(\langle b,c\rangle )$
is at least
$\phi ^s(\langle b,c\rangle )$
is at least
![]() $K+2D$
away from
$K+2D$
away from
![]() $\langle a,b\rangle $
in
$\langle a,b\rangle $
in
![]() ${\mathcal F}(\langle a,b,c\rangle )$
.
${\mathcal F}(\langle a,b,c\rangle )$
.
Now consider any sequence
![]() $(r_i)_i$
with
$(r_i)_i$
with
![]() $r_i \ge r$
for all i. By Lemma 5.1 and Theorem 5.4, the projections of
$r_i \ge r$
for all i. By Lemma 5.1 and Theorem 5.4, the projections of
![]() $A_{j-2}$
and
$A_{j-2}$
and
![]() $A_{j+2}$
to
$A_{j+2}$
to
![]() ${\mathcal F}(A_j)$
are defined. Moreover, by Equation 2, we see that, by applying an automorphism, the distance between projections of
${\mathcal F}(A_j)$
are defined. Moreover, by Equation 2, we see that, by applying an automorphism, the distance between projections of
![]() $A_{j-2}$
and
$A_{j-2}$
and
![]() $A_{j+2}$
in
$A_{j+2}$
in
![]() ${\mathcal F}(A_j)$
is the same as the distance between the projections of
${\mathcal F}(A_j)$
is the same as the distance between the projections of
![]() $A_0 = \langle d, e, f \rangle $
and
$A_0 = \langle d, e, f \rangle $
and
![]() $\phi _{r_{j-1}}(A_3) = \langle \phi _{r_{j-1}}(b),\phi _{r_{j-1}}(c),a \rangle $
to
$\phi _{r_{j-1}}(A_3) = \langle \phi _{r_{j-1}}(b),\phi _{r_{j-1}}(c),a \rangle $
to
![]() ${\mathcal F}(A_2) = {\mathcal F}(\langle e, f, g \rangle )$
. Note that the rotation
${\mathcal F}(A_2) = {\mathcal F}(\langle e, f, g \rangle )$
. Note that the rotation
![]() $\rho $
sends the free factor
$\rho $
sends the free factor
![]() $\langle a,b,c\rangle $
to
$\langle a,b,c\rangle $
to
![]() $A_2$
, thus inducing an isometry from
$A_2$
, thus inducing an isometry from
![]() ${\mathcal F}(\langle a,b,c\rangle )$
to
${\mathcal F}(\langle a,b,c\rangle )$
to
![]() ${\mathcal F}(A_2)$
. The projection of
${\mathcal F}(A_2)$
. The projection of
![]() $A_0$
to
$A_0$
to
![]() ${\mathcal F}(A_2)$
is D-close to the factor
${\mathcal F}(A_2)$
is D-close to the factor
![]() $\langle e,f\rangle = \rho (\langle a,b \rangle )$
, and the projection of
$\langle e,f\rangle = \rho (\langle a,b \rangle )$
, and the projection of
![]() $\phi _{r_{j-1}}(A_3)$
to
$\phi _{r_{j-1}}(A_3)$
to
![]() ${\mathcal F}(A_2)$
is D-close to the factor
${\mathcal F}(A_2)$
is D-close to the factor
![]() $\rho \phi ^{r_{j-1}}(\langle b,c \rangle )$
. Thus, the distance in
$\rho \phi ^{r_{j-1}}(\langle b,c \rangle )$
. Thus, the distance in
![]() ${\mathcal F}(A_2)$
of the two projections is at least K. This shows the first statement of the lemma.
${\mathcal F}(A_2)$
of the two projections is at least K. This shows the first statement of the lemma.
Now, fix
![]() $K> 3D$
and let
$K> 3D$
and let
![]() $(r_i)_i$
be any sequence with
$(r_i)_i$
be any sequence with
![]() $r_i \ge r(K)$
for all i. We will prove the second statement by inducting on
$r_i \ge r(K)$
for all i. We will prove the second statement by inducting on
![]() $l=k-i$
with the previous statement giving the base case
$l=k-i$
with the previous statement giving the base case
![]() $l = 4$
. Suppose we are given
$l = 4$
. Suppose we are given
![]() $A_i,A_j,A_k$
with
$A_i,A_j,A_k$
with
![]() $l=k-i>4$
,
$l=k-i>4$
,
![]() $j-i,k-j\geq 2$
. We first claim that projections of
$j-i,k-j\geq 2$
. We first claim that projections of
![]() $A_{j+2},A_{j+3},\cdots , A_k$
to
$A_{j+2},A_{j+3},\cdots , A_k$
to
![]() ${\mathcal F}(A_j)$
are defined, that is, none of them are equal to or disjoint from
${\mathcal F}(A_j)$
are defined, that is, none of them are equal to or disjoint from
![]() $A_j$
. For suppose
$A_j$
. For suppose
![]() $A_s$
is the first on the list that is equal to or disjoint from
$A_s$
is the first on the list that is equal to or disjoint from
![]() $A_j$
. By Lemma 5.1, we have
$A_j$
. By Lemma 5.1, we have
![]() $4\leq s-j < k-i$
. By induction, the projections of both
$4\leq s-j < k-i$
. By induction, the projections of both
![]() $A_j$
and
$A_j$
and
![]() $A_s$
to
$A_s$
to
![]() ${\mathcal F}(A_{j+2})$
are defined and the distance between their projections is
${\mathcal F}(A_{j+2})$
are defined and the distance between their projections is
![]() $\geq K-2D> D$
. Using statement 2 of Theorem 5.4, this implies that
$\geq K-2D> D$
. Using statement 2 of Theorem 5.4, this implies that
![]() $A_s$
and
$A_s$
and
![]() $A_j$
cannot coincide or be disjoint, proving the claim. By the same argument, we also have that the projections of
$A_j$
cannot coincide or be disjoint, proving the claim. By the same argument, we also have that the projections of
![]() $A_i,A_{i+1},\cdots ,A_{j-2}$
to
$A_i,A_{i+1},\cdots ,A_{j-2}$
to
![]() ${\mathcal F}(A_j)$
are all defined.
${\mathcal F}(A_j)$
are all defined.
By the first statement of the lemma, we have
![]() $d_{A_j}(A_{j-2},A_{j+2}) \ge K$
. We now claim that
$d_{A_j}(A_{j-2},A_{j+2}) \ge K$
. We now claim that
![]() $d_{A_j}(A_{j+2}, A_k) \le D$
. If
$d_{A_j}(A_{j+2}, A_k) \le D$
. If
![]() $k=j+3$
, then
$k=j+3$
, then
![]() $A_{j+2}$
and
$A_{j+2}$
and
![]() $A_k$
are disjoint, and the claim holds by statement 2 of Theorem 5.4. If
$A_k$
are disjoint, and the claim holds by statement 2 of Theorem 5.4. If
![]() $k \ge j+4$
, then applying induction again to j,
$k \ge j+4$
, then applying induction again to j,
![]() $j+2$
and k, we see that
$j+2$
and k, we see that
![]() $A_j$
and
$A_j$
and
![]() $A_k$
have well-defined projections to
$A_k$
have well-defined projections to
![]() ${\mathcal F}(A_{j+2})$
and
${\mathcal F}(A_{j+2})$
and
![]() $d_{A_{j+2}}(A_j,A_k) \ge K-2D> D$
. Now, the claim follows by the third statement of Theorem 5.4. By the same argument, we also see that
$d_{A_{j+2}}(A_j,A_k) \ge K-2D> D$
. Now, the claim follows by the third statement of Theorem 5.4. By the same argument, we also see that
![]() $d_{A_j}(A_i,A_{j-2}) \le D$
. We now conclude
$d_{A_j}(A_i,A_{j-2}) \le D$
. We now conclude
![]() $d_{A_j}(A_i,A_k) \ge K-2D$
by the triangle inequality.
$d_{A_j}(A_i,A_k) \ge K-2D$
by the triangle inequality.
We are now ready to prove the main results of this section.
Proposition 5.7. There exists
![]() $R>0$
such for any sequence
$R>0$
such for any sequence
![]() $(r_i)_{i \ge 1}$
, if
$(r_i)_{i \ge 1}$
, if
![]() $r_i \ge R$
, and
$r_i \ge R$
, and
![]() $r_i \equiv i$
mod 7, then the sequence
$r_i \equiv i$
mod 7, then the sequence
![]() $(A_i)_{i \ge 0}$
is a quasi-geodesic in
$(A_i)_{i \ge 0}$
is a quasi-geodesic in
![]() ${\mathcal {FF}_{7}}$
.
${\mathcal {FF}_{7}}$
.
Proof. Let D be the constant of Theorem 5.4, and let
![]() $D'$
be the constant of Theorem 5.5. Fix
$D'$
be the constant of Theorem 5.5. Fix
![]() $K=4D+D'$
. Let
$K=4D+D'$
. Let
![]() $R=r(K)$
be the constant of Lemma 5.6. Let
$R=r(K)$
be the constant of Lemma 5.6. Let
![]() $(r_i)_{i \ge 1}$
be any sequence with
$(r_i)_{i \ge 1}$
be any sequence with
![]() $r_i \ge R$
and
$r_i \ge R$
and
![]() $r_i \equiv i$
mod 7 for all i. We will show that the sequence
$r_i \equiv i$
mod 7 for all i. We will show that the sequence
![]() $(A_i)_i$
goes to infinity with linear speed. More precisely, we will show that for any
$(A_i)_i$
goes to infinity with linear speed. More precisely, we will show that for any
![]() $d>0$
, if
$d>0$
, if
![]() $k-i \ge 110d +4$
, then
$k-i \ge 110d +4$
, then
![]() $d_{{\mathcal {FF}_{7}}}(A_i,A_k) \ge d$
. Suppose not. Let
$d_{{\mathcal {FF}_{7}}}(A_i,A_k) \ge d$
. Suppose not. Let
![]() $\gamma $
be a geodesic between
$\gamma $
be a geodesic between
![]() $A_i$
and
$A_i$
and
![]() $A_k$
of length
$A_k$
of length
![]() $< d$
.
$< d$
.
For every
![]() $j \in \{i+2,\ldots ,k-2\}$
, there exists a free factor in
$j \in \{i+2,\ldots ,k-2\}$
, there exists a free factor in
![]() $\gamma $
that is compatible with
$\gamma $
that is compatible with
![]() $A_j$
. Indeed, if every free factor in
$A_j$
. Indeed, if every free factor in
![]() $\gamma $
meets
$\gamma $
meets
![]() $A_j$
, then by Theorem 5.5, projection of
$A_j$
, then by Theorem 5.5, projection of
![]() $\gamma $
to
$\gamma $
to
![]() $A_j$
will be well defined and has diameter bounded by
$A_j$
will be well defined and has diameter bounded by
![]() $D'$
. However, by Lemma 5.6, the projections of
$D'$
. However, by Lemma 5.6, the projections of
![]() $A_i$
and
$A_i$
and
![]() $A_k$
to
$A_k$
to
![]() ${\mathcal F}(A_j)$
has distance at least
${\mathcal F}(A_j)$
has distance at least
![]() $K - 2D> D'$
.
$K - 2D> D'$
.
By the pigeonhole principle, there exists a vertex B of
![]() $\gamma $
compatible with at least 110 free factors among
$\gamma $
compatible with at least 110 free factors among
![]() $\{A_{i+2},\ldots ,A_{k-2}\}$
. By Lemma 5.3, it is not possible for B to be compatible with 109 consecutive
$\{A_{i+2},\ldots ,A_{k-2}\}$
. By Lemma 5.3, it is not possible for B to be compatible with 109 consecutive
![]() $A_j$
’s. Therefore, it must be possible to find
$A_j$
’s. Therefore, it must be possible to find
![]() $i+2 \le i' < j' < k' \le k-2$
with
$i+2 \le i' < j' < k' \le k-2$
with
![]() $j' - i' \ge 2$
and
$j' - i' \ge 2$
and
![]() $k' - j' \ge 2$
such that B is compatible with
$k' - j' \ge 2$
such that B is compatible with
![]() $A_{i'}$
and
$A_{i'}$
and
![]() $A_{k'}$
, but B meets
$A_{k'}$
, but B meets
![]() $A_{j'}$
. In particular,
$A_{j'}$
. In particular,
![]() $\pi _{A_{j'}}(B)$
is defined. By Lemma 5.6,
$\pi _{A_{j'}}(B)$
is defined. By Lemma 5.6,
![]() $A_{i'}$
,
$A_{i'}$
,
![]() $A_{k'}$
also have well-defined projections to
$A_{k'}$
also have well-defined projections to
![]() ${\mathcal F}(A_{j'})$
with
${\mathcal F}(A_{j'})$
with
![]() $d_{A_{j'}}(A_{i'},A_{k'}) \ge K-2D> 2D$
. On the other hand, since B is compatible with both
$d_{A_{j'}}(A_{i'},A_{k'}) \ge K-2D> 2D$
. On the other hand, since B is compatible with both
![]() $A_{i'}$
and
$A_{i'}$
and
![]() $A_{k'}$
, we have
$A_{k'}$
, we have
![]() $d_{A_{j'}}(A_{i'},B) \le D$
and
$d_{A_{j'}}(A_{i'},B) \le D$
and
![]() $d_{A_{j'}}(A_{k'},B)\le D$
by Theorem 5.4. This is a contradiction, finishing the proof that
$d_{A_{j'}}(A_{k'},B)\le D$
by Theorem 5.4. This is a contradiction, finishing the proof that
![]() $d_{{\mathcal {FF}_{7}}}(A_i, A_k) \ge d$
for all
$d_{{\mathcal {FF}_{7}}}(A_i, A_k) \ge d$
for all
![]() $k-i \ge 110d+4$
.
$k-i \ge 110d+4$
.
Recall that
![]() ${\mathcal {FF}_{n}}$
is Gromov hyperbolic and that its Gromov boundary is the space of equivalence class of arational trees. Also, recall we say a folding sequence
${\mathcal {FF}_{n}}$
is Gromov hyperbolic and that its Gromov boundary is the space of equivalence class of arational trees. Also, recall we say a folding sequence
![]() $(G_i)_i$
converges to an arational tree T, if
$(G_i)_i$
converges to an arational tree T, if
![]() $\pi (U_i)$
converges to
$\pi (U_i)$
converges to
![]() $[T] \in \partial {\mathcal {FF}_{n}}$
, where
$[T] \in \partial {\mathcal {FF}_{n}}$
, where
![]() $U_i$
is the open simplex in in
$U_i$
is the open simplex in in
![]() ${\text {CV}_{n}} $
associated to
${\text {CV}_{n}} $
associated to
![]() $G_i$
. We have the following corollary.
$G_i$
. We have the following corollary.
Corollary 5.8. Given any strictly increasing sequence
![]() $(r_i)_{i \geq 1}$
satisfying
$(r_i)_{i \geq 1}$
satisfying
![]() $r_i \equiv i \quad\mod 7$
, the folding sequence
$r_i \equiv i \quad\mod 7$
, the folding sequence
![]() $(\tau _i')_i$
converges to an arational tree T.
$(\tau _i')_i$
converges to an arational tree T.
5.3. Nongeometric tree
We will now show that the arational tree obtained in the previous section as the limit of the free factors
![]() $(A_i)_i$
is nongeometric. This section will use the terminology of band complexes and resolutions; for details see [Reference Bestvina and FeighnBF95].
$(A_i)_i$
is nongeometric. This section will use the terminology of band complexes and resolutions; for details see [Reference Bestvina and FeighnBF95].
Definition 5.9 (Geometric tree)
[Reference Bestvina and FeighnBF94, Reference Levitt and PaulinLP97] Let X be a band complex and T a
![]() $G=\pi _1(X)$
-tree. A resolution
$G=\pi _1(X)$
-tree. A resolution
![]() $f :\widetilde {X} \to T$
is exact if for every G-tree
$f :\widetilde {X} \to T$
is exact if for every G-tree
![]() $T'$
and equivariant factorization
$T'$
and equivariant factorization
of f with
![]() $f'$
a surjective resolution it follows that h is an isometry onto its image. We say T is geometric if every resolution is exact.
$f'$
a surjective resolution it follows that h is an isometry onto its image. We say T is geometric if every resolution is exact.
The proof of the following proposition is based on [Reference Bestvina and FeighnBF94, Proposition 3.6].
Proposition 5.10. For any strictly increasing sequence
![]() $(r_i)_{i \ge 1}$
, if the corresponding folding sequence
$(r_i)_{i \ge 1}$
, if the corresponding folding sequence
![]() $(\tau _i')_i$
converges to an arational tree T, then T is not geometric.
$(\tau _i')_i$
converges to an arational tree T, then T is not geometric.
Proof. Let
![]() $\tilde \psi _i \colon \, \tilde \tau _{i-1}' \to \tilde \tau _i'$
be a lift of the train track map to the universal covers fixing a base vertex. Pick a length measure on
$\tilde \psi _i \colon \, \tilde \tau _{i-1}' \to \tilde \tau _i'$
be a lift of the train track map to the universal covers fixing a base vertex. Pick a length measure on
![]() $(\tau _i')_i$
, so we get a folding sequence
$(\tau _i')_i$
, so we get a folding sequence
![]() $\tilde \tau _0' \stackrel {\tilde \psi _1}{\longrightarrow } \tilde \tau _1' \stackrel {\tilde \psi _2}{\longrightarrow } \cdots $
in
$\tilde \tau _0' \stackrel {\tilde \psi _1}{\longrightarrow } \tilde \tau _1' \stackrel {\tilde \psi _2}{\longrightarrow } \cdots $
in
![]() ${\text {cv}_{7}}$
that converges to T. Recall that there are morphisms
${\text {cv}_{7}}$
that converges to T. Recall that there are morphisms
![]() $h_i \colon \, \tilde {\tau }_i' \to T$
such that
$h_i \colon \, \tilde {\tau }_i' \to T$
such that
![]() $h_i = h_{i+1} \tilde \psi _{i+1}$
. Since T is arational,
$h_i = h_{i+1} \tilde \psi _{i+1}$
. Since T is arational,
![]() $h_i$
’s are not isometries though they restrict to isometries on edges. Let X be a finite band complex with resolution
$h_i$
’s are not isometries though they restrict to isometries on edges. Let X be a finite band complex with resolution
![]() $f \colon \, \tilde X \to T$
. We will show that the resolution factors through
$f \colon \, \tilde X \to T$
. We will show that the resolution factors through
![]() $\tilde \tau _i'$
for sufficiently large i. This will imply T is not geometric.
$\tilde \tau _i'$
for sufficiently large i. This will imply T is not geometric.
Let
![]() $\Gamma $
be the underlying real graph of X (disjoint union of metric arcs) with preimage
$\Gamma $
be the underlying real graph of X (disjoint union of metric arcs) with preimage
![]() $\tilde \Gamma $
in
$\tilde \Gamma $
in
![]() $\tilde X$
. We may assume f embeds the components of
$\tilde X$
. We may assume f embeds the components of
![]() $\tilde \Gamma $
. A vertex v of
$\tilde \Gamma $
. A vertex v of
![]() $\tilde X$
is either a vertex of
$\tilde X$
is either a vertex of
![]() $\tilde \Gamma $
or a corner of a band or a 0-cell of
$\tilde \Gamma $
or a corner of a band or a 0-cell of
![]() $\tilde X$
. For every such vertex v, choose a point
$\tilde X$
. For every such vertex v, choose a point
![]() $f_0(v) \in \tilde \tau _0$
so that
$f_0(v) \in \tilde \tau _0$
so that
![]() $f_0$
is equivariant and
$f_0$
is equivariant and
![]() $f=h_0 f_0$
on the vertices of
$f=h_0 f_0$
on the vertices of
![]() $\tilde X$
.
$\tilde X$
.
An edge in
![]() $\tilde X$
is either a subarc of
$\tilde X$
is either a subarc of
![]() $\tilde \Gamma $
or a vertical boundary component of a band or a one-cell in
$\tilde \Gamma $
or a vertical boundary component of a band or a one-cell in
![]() $\tilde X$
. Up to the action of
$\tilde X$
. Up to the action of
![]() ${\mathbb {F}_{7}}$
, there are only finitely many edges. Using Lemma 4.8, we can find
${\mathbb {F}_{7}}$
, there are only finitely many edges. Using Lemma 4.8, we can find
![]() $i>0$
such that for every edge e in
$i>0$
such that for every edge e in
![]() $\tilde X$
, the edge path in
$\tilde X$
, the edge path in
![]() $\tilde \tau _i'$
joining the two vertices of
$\tilde \tau _i'$
joining the two vertices of
![]() $\tilde \psi _i \cdots \tilde \psi _1 f_0(\partial e)$
is legal. Now, extend
$\tilde \psi _i \cdots \tilde \psi _1 f_0(\partial e)$
is legal. Now, extend
![]() $\tilde \psi _i \cdots \tilde \psi _1 f_0$
to an equivariant map
$\tilde \psi _i \cdots \tilde \psi _1 f_0$
to an equivariant map
![]() $f_i \colon \, \tilde X \to \tilde \tau _i'$
that sends edges to legal paths (or points) and is constant on the leaves. Thus,
$f_i \colon \, \tilde X \to \tilde \tau _i'$
that sends edges to legal paths (or points) and is constant on the leaves. Thus,
![]() $f_i$
is a resolution of
$f_i$
is a resolution of
![]() $\tilde \tau _i'$
.
$\tilde \tau _i'$
.
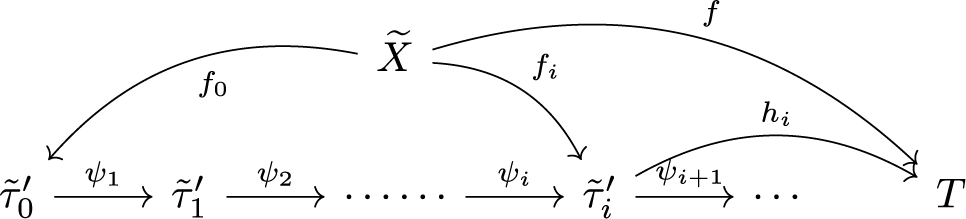
This yields a factorization
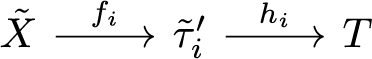
but
![]() $h_i$
is not an isometry. This shows T is nongeometric.
$h_i$
is not an isometry. This shows T is nongeometric.
6. Nonuniquely ergodic unfolding sequence
The goal of this section is to show that if a sequence
![]() $(r_i)_{i \ge 1}$
grows sufficiently fast, then the set of currents supported on the legal lamination
$(r_i)_{i \ge 1}$
grows sufficiently fast, then the set of currents supported on the legal lamination
![]() $\Lambda $
of the unfolding sequence
$\Lambda $
of the unfolding sequence
![]() $(\tau _i)_{i \geq 0}$
is a 1-simplex in
$(\tau _i)_{i \geq 0}$
is a 1-simplex in
![]() ${\mathbb {P}\mathrm {Curr}_{7}}$
.
${\mathbb {P}\mathrm {Curr}_{7}}$
.
Recall that
![]() $M_r$
is a
$M_r$
is a
![]() $7\times 7$
matrix of the block form
$7\times 7$
matrix of the block form
 $$\begin{align*}\begin{pmatrix} 0&I\\ B^r&0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0&I\\ B^r&0 \end{pmatrix}, \end{align*}$$
where I is the
![]() $4\times 4$
identity matrix, and B is the transition matrix of
$4\times 4$
identity matrix, and B is the transition matrix of
![]() $\theta $
; all that matters is that some positive power of B has all entries positive. Let
$\theta $
; all that matters is that some positive power of B has all entries positive. Let
![]() $\lambda _B$
be the Perron–Frobenius eigenvalue of B. Recall the constant
$\lambda _B$
be the Perron–Frobenius eigenvalue of B. Recall the constant
![]() $\kappa _B> 0$
from Lemma 4.5. Given a sequence
$\kappa _B> 0$
from Lemma 4.5. Given a sequence
![]() $(r_i)_i$
, define for each
$(r_i)_i$
, define for each
![]() $i \ge 1$
$i \ge 1$
Let
![]() $\{e_k:k=1,\ldots ,7\}$
be the standard basis for
$\{e_k:k=1,\ldots ,7\}$
be the standard basis for
![]() ${\mathbb R}^7$
. Denote by
${\mathbb R}^7$
. Denote by
![]() $\mathbb P{\mathbb R}_{\geq 0}^7$
the projectivization of
$\mathbb P{\mathbb R}_{\geq 0}^7$
the projectivization of
![]() ${\mathbb R}_{\geq 0}^7$
, and the projective class of a vector v by
${\mathbb R}_{\geq 0}^7$
, and the projective class of a vector v by
![]() $[v]$
. Fix a metric d on
$[v]$
. Fix a metric d on
![]() ${\mathbb P}{\mathbb R}_{\geq 0}^7$
. We view
${\mathbb P}{\mathbb R}_{\geq 0}^7$
. We view
![]() $M_r$
as a projective transformation
$M_r$
as a projective transformation
![]() ${\mathbb P}{\mathbb R}_{\geq 0}^7\to {\mathbb P}{\mathbb R}_{\geq 0}^7$
. For a sequence
${\mathbb P}{\mathbb R}_{\geq 0}^7\to {\mathbb P}{\mathbb R}_{\geq 0}^7$
. For a sequence
![]() $(r_i)_{i \geq 1}$
and for
$(r_i)_{i \geq 1}$
and for
![]() $i<j$
denote by
$i<j$
denote by
![]() $S_{i,j}\subset \mathbb P {\mathbb R}_{\geq 0}^7$
the image of the composition
$S_{i,j}\subset \mathbb P {\mathbb R}_{\geq 0}^7$
the image of the composition
and by
![]() $S_i=\bigcap _{j>i}S_{i,j}$
. We denote by
$S_i=\bigcap _{j>i}S_{i,j}$
. We denote by
![]() $v_B$
a positive Perron–Frobenius eigenvector of B, and by
$v_B$
a positive Perron–Frobenius eigenvector of B, and by
![]() $v_B^{234}$
(resp.
$v_B^{234}$
(resp.
![]() $v_B^{567}$
) the vector in
$v_B^{567}$
) the vector in
![]() ${\mathbb R}^7$
which is
${\mathbb R}^7$
which is
![]() $v_B$
in coordinates
$v_B$
in coordinates
![]() $2,3,4$
(resp.
$2,3,4$
(resp.
![]() $5,6,7$
) and 0 in all other coordinates. The main result of this section is the following.
$5,6,7$
) and 0 in all other coordinates. The main result of this section is the following.
Proposition 6.1. Let
![]() $(r_i)_{i \ge 1}$
be a sequence of positive integers with
$(r_i)_{i \ge 1}$
be a sequence of positive integers with
![]() $r_{i+1}-r_i \ge i$
. Then for all i the set
$r_{i+1}-r_i \ge i$
. Then for all i the set
![]() $S_i$
is a 1-simplex, that is, it is the convex hull of two distinct points
$S_i$
is a 1-simplex, that is, it is the convex hull of two distinct points
![]() $p_i,q_i\in \mathbb P {\mathbb R}_{> 0}^7$
. Moreover, as
$p_i,q_i\in \mathbb P {\mathbb R}_{> 0}^7$
. Moreover, as
![]() $i\to \infty $
,
$i\to \infty $
,
![]() $\{p_i,q_i\}$
converges (as a set) to
$\{p_i,q_i\}$
converges (as a set) to
![]() $\{ [v_B^{234}], [v_B^{567}]\}$
.
$\{ [v_B^{234}], [v_B^{567}]\}$
.
Before we give a technical proof of Proposition 6.1, we will give a simpler, more intuitive proof where the sequence
![]() $r_1<r_2<\cdots $
is chosen inductively so that
$r_1<r_2<\cdots $
is chosen inductively so that
![]() $r_1$
is sufficiently large and each
$r_1$
is sufficiently large and each
![]() $r_i$
is sufficiently large depending on
$r_i$
is sufficiently large depending on
![]() $r_1,r_2,\cdots ,r_{i-1}$
. Later, we do a more careful analysis where we can control the growth of the sequence.
$r_1,r_2,\cdots ,r_{i-1}$
. Later, we do a more careful analysis where we can control the growth of the sequence.
Proof idea of Proposition 6.1
For
![]() $\epsilon>0$
, we will write
$\epsilon>0$
, we will write
![]() $x\overset {\epsilon }=y$
if
$x\overset {\epsilon }=y$
if
![]() $d(x,y)<\epsilon $
in
$d(x,y)<\epsilon $
in
![]() ${\mathbb P}{\mathbb R}_{\geq 0}^7$
. Each
${\mathbb P}{\mathbb R}_{\geq 0}^7$
. Each
![]() $S_{ij}$
is the convex hull of the
$S_{ij}$
is the convex hull of the
![]() $M_{ij}$
-images of the vectors
$M_{ij}$
-images of the vectors
![]() $e_i$
,
$e_i$
,
![]() $i=1,\cdots ,7$
. The proof consists of computing these images using the Perron–Frobenius dynamics. We first observe that there is a sequence
$i=1,\cdots ,7$
. The proof consists of computing these images using the Perron–Frobenius dynamics. We first observe that there is a sequence
![]() $\epsilon _r\to 0$
such that
$\epsilon _r\to 0$
such that
-
•
 $M_r(e_7)=e_4$
,
$M_r(e_7)=e_4$
,
 $M_r(e_6)=e_3$
,
$M_r(e_6)=e_3$
,
 $M_r(e_5)=e_2$
,
$M_r(e_5)=e_2$
,
 $M_r(e_4)=e_1$
,
$M_r(e_4)=e_1$
, -
•
 $M_r(e_i)\overset {\epsilon _r}=v_B^{567}$
,
$M_r(e_i)\overset {\epsilon _r}=v_B^{567}$
,
 $i=1,2,3$
,
$i=1,2,3$
, -
•
 $M_r(v_B^{567})=v_B^{234}$
,
$M_r(v_B^{567})=v_B^{234}$
,
 $M_r(v_B^{234})\overset {\epsilon _r}=v_B^{567}$
.
$M_r(v_B^{234})\overset {\epsilon _r}=v_B^{567}$
.
Next, we consider the composition
![]() $M_sM_r$
for
$M_sM_r$
for
![]() $r>>s$
. The third bullet uses uniform continuity of
$r>>s$
. The third bullet uses uniform continuity of
![]() $M_s$
and the assumption that r is sufficiently large compared to s.
$M_s$
and the assumption that r is sufficiently large compared to s.
-
•
 $M_sM_r(e_7)=e_1$
,
$M_sM_r(e_7)=e_1$
, -
•
 $M_sM_r(e_i)\overset {\epsilon _s}=v_B^{567}$
,
$M_sM_r(e_i)\overset {\epsilon _s}=v_B^{567}$
,
 $i=4,5,6$
,
$i=4,5,6$
, -
•
 $M_sM_r(e_i)\overset {\epsilon _s}=v_B^{234}$
,
$M_sM_r(e_i)\overset {\epsilon _s}=v_B^{234}$
,
 $i=1,2,3$
.
$i=1,2,3$
.
Finally, for
![]() $r>>s>>t$
we see similarly:
$r>>s>>t$
we see similarly:
-
•
 $M_tM_sM_r(e_7)\overset {\epsilon _t}=v_B^{567}$
,
$M_tM_sM_r(e_7)\overset {\epsilon _t}=v_B^{567}$
, -
•
 $M_tM_sM_r(e_i)\overset {\epsilon _t}=v_B^{234}$
,
$M_tM_sM_r(e_i)\overset {\epsilon _t}=v_B^{234}$
,
 $i=4,5,6$
,
$i=4,5,6$
, -
•
 $M_tM_sM_r(e_i)\overset {\epsilon _t}=v_B^{567}$
,
$M_tM_sM_r(e_i)\overset {\epsilon _t}=v_B^{567}$
,
 $i=1,2,3$
.
$i=1,2,3$
.
It follows that if we make suitably large choices for the
![]() $r_i$
’s, the set
$r_i$
’s, the set
![]() $S_{i,i+3}$
will be contained in the
$S_{i,i+3}$
will be contained in the
![]() $\epsilon _{r_i}$
-neighborhood of the 1-simplex
$\epsilon _{r_i}$
-neighborhood of the 1-simplex
![]() $[v_B^{567},v_B^{234}]$
. Moreover, given any
$[v_B^{567},v_B^{234}]$
. Moreover, given any
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $j>i+3$
we can choose
$j>i+3$
we can choose
![]() $r_j$
large (depending on uniform continuity constants of
$r_j$
large (depending on uniform continuity constants of
![]() $M_{ij}$
) to ensure that
$M_{ij}$
) to ensure that
![]() $S_{i,j+3}=M_{ij}(S_{j,j+3})$
is contained in the
$S_{i,j+3}=M_{ij}(S_{j,j+3})$
is contained in the
![]() $\epsilon $
-neighborhood of the 1-simplex with endpoints
$\epsilon $
-neighborhood of the 1-simplex with endpoints
![]() $M_{ij}(v_B^{567})$
and
$M_{ij}(v_B^{567})$
and
![]() $M_{ij}(v_B^{234})$
. Thus, each
$M_{ij}(v_B^{234})$
. Thus, each
![]() $S_i$
is the nested intersection of simplices of dimension
$S_i$
is the nested intersection of simplices of dimension
![]() $\leq 6$
such that for all
$\leq 6$
such that for all
![]() $\epsilon>0$
they are eventually all contained in the
$\epsilon>0$
they are eventually all contained in the
![]() $\epsilon $
-neighborhood of a 1-simplex with definite distance between the endpoints. This proves the proposition.
$\epsilon $
-neighborhood of a 1-simplex with definite distance between the endpoints. This proves the proposition.
We now present a more detailed proof of Proposition 6.1. For a sequence of integers
![]() $(r_i)_{i\geq 1}$
such that
$(r_i)_{i\geq 1}$
such that
![]() $r_i, r_{i+1}-r_i \to \infty $
, by Lemma 4.5
$r_i, r_{i+1}-r_i \to \infty $
, by Lemma 4.5
![]() $(P_i)_i$
converges to an idempotent matrix Y. Let
$(P_i)_i$
converges to an idempotent matrix Y. Let
![]() $\Delta _i = Y - P_i$
and let
$\Delta _i = Y - P_i$
and let
![]() $||Y||$
be the operator norm.
$||Y||$
be the operator norm.
Lemma 6.2. Let
![]() $(r_i)_{i\geq 1}$
be a sequence of positive integers such that
$(r_i)_{i\geq 1}$
be a sequence of positive integers such that
![]() $r_{i+1}-r_i \ge i$
. Then there exists an
$r_{i+1}-r_i \ge i$
. Then there exists an
![]() $I \geq 1$
such that for all
$I \geq 1$
such that for all
![]() $i \geq I$
,
$i \geq I$
,
![]() $||\Delta _i|| \leq 1/(2 \cdot 2^i)$
.
$||\Delta _i|| \leq 1/(2 \cdot 2^i)$
.
Proof. Let
![]() $\lambda _B, \mu _B, \mu ^{\prime }_B$
be the modulus of the three eigenvalues of B; we have
$\lambda _B, \mu _B, \mu ^{\prime }_B$
be the modulus of the three eigenvalues of B; we have
![]() $\lambda _B \sim 1.46$
and
$\lambda _B \sim 1.46$
and
![]() $\mu _B = \mu ^{\prime }_B \sim 0.826$
. Then
$\mu _B = \mu ^{\prime }_B \sim 0.826$
. Then
 $$\begin{align*}||\Delta_i|| = || P_i - Y || \leq \text{ max } \left( \frac{\mu^{r_{i+1}}}{\lambda^{r_{i+1}}}, \frac{\lambda^{r_{i}}}{\lambda^{r_{i+1}}} \right) \leq \frac{\lambda^{r_{i}}}{\lambda^{r_{i+1}}}, \end{align*}$$
$$\begin{align*}||\Delta_i|| = || P_i - Y || \leq \text{ max } \left( \frac{\mu^{r_{i+1}}}{\lambda^{r_{i+1}}}, \frac{\lambda^{r_{i}}}{\lambda^{r_{i+1}}} \right) \leq \frac{\lambda^{r_{i}}}{\lambda^{r_{i+1}}}, \end{align*}$$
where the two terms comes from the two blocks in
![]() $P_i$
. For the last inequality, note that
$P_i$
. For the last inequality, note that
![]() $\mu < 1 < \lambda $
and
$\mu < 1 < \lambda $
and
![]() $r_i$
are positive integers. Therefore,
$r_i$
are positive integers. Therefore,
![]() $\mu ^{r_{i+1}} < 1 < \lambda ^{r_i}$
.
$\mu ^{r_{i+1}} < 1 < \lambda ^{r_i}$
.
Now, we claim that there exists an
![]() $I \geq 1$
such that for all
$I \geq 1$
such that for all
![]() $i\geq I$
,
$i\geq I$
,
We only need to show that the sequence
![]() $\frac {r_{i+1}-r_i}{i+1}$
is eventually increasing. Indeed, by assumption,
$\frac {r_{i+1}-r_i}{i+1}$
is eventually increasing. Indeed, by assumption,
![]() $r_{i+1}-r_i \ge i$
, so
$r_{i+1}-r_i \ge i$
, so
 $$ \begin{align*} i & \leq r_{i+1}-r_i \\ \frac{ i}{i+1} & \leq \frac{r_{i+1}-r_i}{i+1}. \end{align*} $$
$$ \begin{align*} i & \leq r_{i+1}-r_i \\ \frac{ i}{i+1} & \leq \frac{r_{i+1}-r_i}{i+1}. \end{align*} $$
Since
![]() $i/(i+1)$
is an increasing sequence, it follows that our sequence is also increasing.
$i/(i+1)$
is an increasing sequence, it follows that our sequence is also increasing.
The following lemma is a consequence of Lemma 4.5 and Lemma A.1.
Lemma 6.3. Let
![]() $(r_i)_{i \ge 1}$
be a sequence of positive integers such that
$(r_i)_{i \ge 1}$
be a sequence of positive integers such that
![]() $r_{i+1}-r_i \ge i$
, Y be the idempotent matrix of Lemma 4.5 and
$r_{i+1}-r_i \ge i$
, Y be the idempotent matrix of Lemma 4.5 and
![]() $M_\infty = \lim _{r \to \infty } M_r/\lambda _B^r$
. Then the following statements hold.
$M_\infty = \lim _{r \to \infty } M_r/\lambda _B^r$
. Then the following statements hold.
-
(1) For all
 $i \ge 1$
, the sequence of matrices
$i \ge 1$
, the sequence of matrices
 $\{ P_i P_{i+2} \cdots P_{i+2k}\}_{k=1}^\infty $
converges to a matrix
$\{ P_i P_{i+2} \cdots P_{i+2k}\}_{k=1}^\infty $
converges to a matrix
 $Y_i$
. Furthermore, for all sufficiently large i,
$Y_i$
. Furthermore, for all sufficiently large i,  $$\begin{align*}\left\lVert Y_i - Y\right\rVert \le \frac{2}{2^i}\left( \left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \right).\end{align*}$$
$$\begin{align*}\left\lVert Y_i - Y\right\rVert \le \frac{2}{2^i}\left( \left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \right).\end{align*}$$
-
(2) The kernel of Y is a subspace of the kernel of
 $Y_i$
for all
$Y_i$
for all
 $i \ge 1$
.
$i \ge 1$
. -
(3) For all
 $i \ge 1$
,
$i \ge 1$
,
 $Y_i(e_1) \neq 0$
with nonnegative entries and
$Y_i(e_1) \neq 0$
with nonnegative entries and
 $Y_i(e_2)$
and
$Y_i(e_2)$
and
 $Y_i(e_3)$
are positive multiples of
$Y_i(e_3)$
are positive multiples of
 $Y_i(e_1)$
.
$Y_i(e_1)$
. -
(4) For all
 $i \ge 1$
,
$i \ge 1$
,
 $M_{r_i} Y_{i+1}(e_1) \neq 0$
with nonnegative entries, and
$M_{r_i} Y_{i+1}(e_1) \neq 0$
with nonnegative entries, and
 $M_{r_i}Y_{i+1}(e_1)$
and
$M_{r_i}Y_{i+1}(e_1)$
and
 $Y_i(e_1)$
are not scalar multiples of each other.
$Y_i(e_1)$
are not scalar multiples of each other. -
(5) Projectively,
 $[Y_i(e_1)] \to [Y(e_1)]$
and
$[Y_i(e_1)] \to [Y(e_1)]$
and
 $[M_{r_i}Y_{i+1}(e_1)] \to [M_\infty Y(e_1)]$
as
$[M_{r_i}Y_{i+1}(e_1)] \to [M_\infty Y(e_1)]$
as
 $i \to \infty $
.
$i \to \infty $
.
Proof. For (1), it suffices to show convergence for all i greater than some I. Indeed, if such I exists and
![]() $i < I$
, then let
$i < I$
, then let
![]() $i_0 \ge I$
be such that
$i_0 \ge I$
be such that
![]() $i = i_0$
(mod 2) and observe that
$i = i_0$
(mod 2) and observe that
By assumption,
![]() $\{P_{i_0}P_{i_0+2} \cdots P_{i_0+2k}\}_{k=0}^\infty $
converges. Since matrix multiplication is continuous, the sequence
$\{P_{i_0}P_{i_0+2} \cdots P_{i_0+2k}\}_{k=0}^\infty $
converges. Since matrix multiplication is continuous, the sequence
![]() $\{P_iP_{i+2} \cdots P_{i+2k}\}_{k=0}^\infty $
also converges.
$\{P_iP_{i+2} \cdots P_{i+2k}\}_{k=0}^\infty $
also converges.
For each i, let
By Lemma 6.2, there exists
![]() $I \ge 1$
such that for all
$I \ge 1$
such that for all
![]() $i \ge I$
,
$i \ge I$
,
![]() $\left \lVert \Delta _i\right \rVert \le \frac {1}{2 \cdot 2^i}$
. Also, choose I sufficiently large so that
$\left \lVert \Delta _i\right \rVert \le \frac {1}{2 \cdot 2^i}$
. Also, choose I sufficiently large so that
![]() $\frac {1}{2^I} \left \lVert Y\right \rVert \le 1/2$
. Then, by Lemma A.1, for all
$\frac {1}{2^I} \left \lVert Y\right \rVert \le 1/2$
. Then, by Lemma A.1, for all
![]() $i \ge I$
, the sequence
$i \ge I$
, the sequence
![]() $\{ P_i P_{i+2} \cdots P_{i+2k}\}_{k=0}^\infty $
converges to some matrix
$\{ P_i P_{i+2} \cdots P_{i+2k}\}_{k=0}^\infty $
converges to some matrix
![]() $Y_i$
, with
$Y_i$
, with
For (2), it again suffices to show the statement is true for all sufficiently large i, and the statement holds for all
![]() $i \ge I$
by Lemma A.1.
$i \ge I$
by Lemma A.1.
For (3), first note that since all the matrices involved are nonnegative, the resulting vectors are all also nonnegative. So we only need to show that they are not the zero vector. It suffices to check that
![]() $Y_i(e_1) \neq 0$
for all sufficiently large i since each
$Y_i(e_1) \neq 0$
for all sufficiently large i since each
![]() $P_i$
is nonnegative and has full rank. For large i, the statement follows because
$P_i$
is nonnegative and has full rank. For large i, the statement follows because
![]() $Y(e_1)$
is not equal to 0 and
$Y(e_1)$
is not equal to 0 and
![]() $\left \lVert Y_i(e_1) - Y(e_1)\right \rVert \le \left \lVert Y_i-Y\right \rVert $
can be made arbitrarily small. For the second statement, we know that
$\left \lVert Y_i(e_1) - Y(e_1)\right \rVert \le \left \lVert Y_i-Y\right \rVert $
can be made arbitrarily small. For the second statement, we know that
![]() $Y(e_2)$
and
$Y(e_2)$
and
![]() $Y(e_3)$
are positive multiples of
$Y(e_3)$
are positive multiples of
![]() $Y(e_1)$
, so there are
$Y(e_1)$
, so there are
![]() $s,t> 0$
such that
$s,t> 0$
such that
![]() $se_2 - e_1$
and
$se_2 - e_1$
and
![]() $te_3 - e_1$
are in the kernel of Y. Then
$te_3 - e_1$
are in the kernel of Y. Then
![]() $Y_i(se_2-e_1) = Y_i(te_3-e_1)=0$
for all i by (2).
$Y_i(se_2-e_1) = Y_i(te_3-e_1)=0$
for all i by (2).
For (4),
![]() $M_{r_i}Y_{i+1}(e_1) \neq 0$
with nonnegative entries since
$M_{r_i}Y_{i+1}(e_1) \neq 0$
with nonnegative entries since
![]() $Y_{i+1}(e_1)$
is so by (3). To see that
$Y_{i+1}(e_1)$
is so by (3). To see that
![]() $M_{r_i}Y_{i+1}(e_1)$
and
$M_{r_i}Y_{i+1}(e_1)$
and
![]() $Y_i(e_1)$
are projectively distinct, it is enough to do this for all sufficiently large i. Let
$Y_i(e_1)$
are projectively distinct, it is enough to do this for all sufficiently large i. Let
![]() $M_\infty = \lim _{r \to \infty } M_r/\lambda _B^r$
. By Lemma 4.5 and Lemma 4.7,
$M_\infty = \lim _{r \to \infty } M_r/\lambda _B^r$
. By Lemma 4.5 and Lemma 4.7,
![]() $Y(e_1)$
and
$Y(e_1)$
and
![]() $M_\infty Y (e_1)$
are orthogonal. Since
$M_\infty Y (e_1)$
are orthogonal. Since
![]() $r_i \to \infty $
, we can make
$r_i \to \infty $
, we can make
![]() $\frac {M_{r_i}}{\lambda _B^{r_i}}Y_{i+1}(e_1)$
arbitrarily close to
$\frac {M_{r_i}}{\lambda _B^{r_i}}Y_{i+1}(e_1)$
arbitrarily close to
![]() $M_\infty Y(e_1)$
, and
$M_\infty Y(e_1)$
, and
![]() $Y_i(e_1)$
close to
$Y_i(e_1)$
close to
![]() $Y(e_1)$
. This means
$Y(e_1)$
. This means
![]() $M_{r_i} Y_{i+1}(e_1)$
and
$M_{r_i} Y_{i+1}(e_1)$
and
![]() $Y_i(e_1)$
are near orthogonal, so they can’t be scalar multiples of each other.
$Y_i(e_1)$
are near orthogonal, so they can’t be scalar multiples of each other.
Statement (5) is clear.
Proof of Proposition 6.1
By Lemma 4.5 and Lemma 4.7,
![]() $[v_B^{234}]=[Y(e_1)]$
and
$[v_B^{234}]=[Y(e_1)]$
and
![]() $[v_B^{567}]=[M_\infty Y(e_1)]$
. Using notation from Lemma 6.3, set
$[v_B^{567}]=[M_\infty Y(e_1)]$
. Using notation from Lemma 6.3, set
By Lemma 6.3 (3)–(5),
-
•
 $p_i$
and
$p_i$
and
 $q_i$
are well defined and distinct.
$q_i$
are well defined and distinct. -
•
 $p_i = [Y_i(e_k)]$
, and
$p_i = [Y_i(e_k)]$
, and
 $q_i = [M_{r_i}Y_{i+1}(e_k)]$
, for
$q_i = [M_{r_i}Y_{i+1}(e_k)]$
, for
 $k=1,2,3$
.
$k=1,2,3$
. -
•
 $p_i \to [v_B^{234}]$
and
$p_i \to [v_B^{234}]$
and
 $q_i \to [v_B^{567}]$
.
$q_i \to [v_B^{567}]$
. -
•
 $[M_{r_i}(p_{i+1})] = q_i$
and
$[M_{r_i}(p_{i+1})] = q_i$
and
 $[M_{r_i}(q_{i+1})] = p_i$
.
$[M_{r_i}(q_{i+1})] = p_i$
.
Our goal is to show
![]() $S_i$
is the
$S_i$
is the
![]() $1$
-simplex spanned by
$1$
-simplex spanned by
![]() $p_i$
and
$p_i$
and
![]() $q_i$
. To do this, we consider
$q_i$
. To do this, we consider
![]() $S_{ij}$
, which is the convex hull of the
$S_{ij}$
, which is the convex hull of the
![]() $M_{ij}$
-images of the vectors
$M_{ij}$
-images of the vectors
![]() $e_k$
,
$e_k$
,
![]() $k=1,\cdots ,7$
. That is, we have to show that
$k=1,\cdots ,7$
. That is, we have to show that
![]() $[M_{ij}(e_k)]$
is close to either
$[M_{ij}(e_k)]$
is close to either
![]() $p_i$
or
$p_i$
or
![]() $q_i$
for each k. We first observe that for all
$q_i$
for each k. We first observe that for all
![]() $r,s> 0$
:
$r,s> 0$
:
-
•
 $M_r(e_4)=e_1$
,
$M_r(e_4)=e_1$
,
 $M_r(e_5)=e_2$
,
$M_r(e_5)=e_2$
,
 $M_r(e_6)=e_3$
,
$M_r(e_6)=e_3$
,
 $M_r(e_7)=e_4$
,
$M_r(e_7)=e_4$
, -
•
 $M_rM_s(e_7)=e_1$
.
$M_rM_s(e_7)=e_1$
.
We may assume that
![]() $j-1 = i+2m$
, so
$j-1 = i+2m$
, so
![]() $M_{ij}$
breaks up into pairs, that is, for all k,
$M_{ij}$
breaks up into pairs, that is, for all k,
Let
![]() $\epsilon> 0$
be arbitrary. Choose
$\epsilon> 0$
be arbitrary. Choose
![]() $\delta> 0$
such that for any vector
$\delta> 0$
such that for any vector
![]() $u \in {\mathbb R}_+^7$
and any
$u \in {\mathbb R}_+^7$
and any
![]() $v \in \left \{ Y_i(e_k), \frac {M_{r_i}}{\lambda _B^{r_i}} Y_{i+1}(e_k) : k=1,2,3\right \}$
, if
$v \in \left \{ Y_i(e_k), \frac {M_{r_i}}{\lambda _B^{r_i}} Y_{i+1}(e_k) : k=1,2,3\right \}$
, if
![]() $\left \lVert u-v\right \rVert \le \delta $
, then
$\left \lVert u-v\right \rVert \le \delta $
, then
![]() $d([u],[v]) \le \epsilon $
. Now, by Lemma 6.3, we can choose J sufficiently large so that whenever
$d([u],[v]) \le \epsilon $
. Now, by Lemma 6.3, we can choose J sufficiently large so that whenever
![]() $i+2m \ge J$
, then
$i+2m \ge J$
, then
-
•
 $\left \lVert P_i \cdots P_{i+2m} -Y_i\right \rVert \le \delta $
$\left \lVert P_i \cdots P_{i+2m} -Y_i\right \rVert \le \delta $
-
•
 $\left \lVert P_{i+1} \cdots P_{i+2m+1} -Y_{i+1}\right \rVert \le \frac {\delta }{\left \lVert M_{r_i}/\lambda _B^{r_i}\right \rVert }.$
$\left \lVert P_{i+1} \cdots P_{i+2m+1} -Y_{i+1}\right \rVert \le \frac {\delta }{\left \lVert M_{r_i}/\lambda _B^{r_i}\right \rVert }.$
Now, we may assume that
![]() $j-3 \ge J$
. Then,
$j-3 \ge J$
. Then,
-
• For
 $k=1,2,3$
, we have
$k=1,2,3$
, we have  $$\begin{align*}\left\lVert P_i \cdots P_{j-1}(e_k) - Y_i(e_k)\right\rVert \le \delta \quad \Longrightarrow \quad d \Big( [ M_{ij} (e_k) ], p_i \Big) \le \epsilon. \end{align*}$$
$$\begin{align*}\left\lVert P_i \cdots P_{j-1}(e_k) - Y_i(e_k)\right\rVert \le \delta \quad \Longrightarrow \quad d \Big( [ M_{ij} (e_k) ], p_i \Big) \le \epsilon. \end{align*}$$
-
• For
 $k=7$
, we have
$k=7$
, we have
 $M_{ij}(e_7) = M_{i,j-2}(e_1)$
, so
$M_{ij}(e_7) = M_{i,j-2}(e_1)$
, so
 $[M_{ij}(e_7)]=[P_i \cdots P_{j-3}(e_1)]$
is
$[M_{ij}(e_7)]=[P_i \cdots P_{j-3}(e_1)]$
is
 $\epsilon $
-close to
$\epsilon $
-close to
 $[p_i]$
by the same reasoning as the previous bullet point.
$[p_i]$
by the same reasoning as the previous bullet point. -
• For
 $k=4,5,6$
,
$k=4,5,6$
,
 $M_{ij}(e_k) = M_{i,j-1}(e_{k-3})$
. In this case, we consider
$M_{ij}(e_k) = M_{i,j-1}(e_{k-3})$
. In this case, we consider
 $\frac {M_{r_i}}{\lambda ^{r_i}} P_{i+1} \cdots P_{j-2}(e_{k-3})$
and approximate it by
$\frac {M_{r_i}}{\lambda ^{r_i}} P_{i+1} \cdots P_{j-2}(e_{k-3})$
and approximate it by
 $\frac {M_{r_i}}{\lambda ^{r_i}} Y_{i+1}(e_{k-3})$
, as follows: Thus, for
$\frac {M_{r_i}}{\lambda ^{r_i}} Y_{i+1}(e_{k-3})$
, as follows: Thus, for $$ \begin{align*} & \left\lVert\frac{M_{r_i}}{\lambda^{r_i}} P_{i+1} \cdots P_{j-2}(e_{k-3}) - \frac{M_{r_i}}{\lambda^{r_i}} Y_{i+1}(e_{k-3})\right\rVert \\ & \le \left\lVert\frac{M_{r_i}}{\lambda^{r_i}}\right\rVert \left\lVert P_{i+1} \cdots P_{j-2} - Y_{i+1}\right\rVert\\ & \le \delta. \end{align*} $$
$$ \begin{align*} & \left\lVert\frac{M_{r_i}}{\lambda^{r_i}} P_{i+1} \cdots P_{j-2}(e_{k-3}) - \frac{M_{r_i}}{\lambda^{r_i}} Y_{i+1}(e_{k-3})\right\rVert \\ & \le \left\lVert\frac{M_{r_i}}{\lambda^{r_i}}\right\rVert \left\lVert P_{i+1} \cdots P_{j-2} - Y_{i+1}\right\rVert\\ & \le \delta. \end{align*} $$
 $k=4,5,6$
,
$k=4,5,6$
,
 $d \Big ( [M_{ij}(e_k)], q_i \Big ) \le \epsilon $
.
$d \Big ( [M_{ij}(e_k)], q_i \Big ) \le \epsilon $
.
We have shown that for any
![]() $\epsilon $
, the vertices of the simplex
$\epsilon $
, the vertices of the simplex
![]() $S_{i,j}$
come
$S_{i,j}$
come
![]() $\epsilon $
-close to
$\epsilon $
-close to
![]() $p_i$
and
$p_i$
and
![]() $q_i$
for all sufficiently large j. Since
$q_i$
for all sufficiently large j. Since
![]() $S_{i,j+1} \subset S_{i,j}$
and
$S_{i,j+1} \subset S_{i,j}$
and
![]() $S_i = \bigcap _{j>i} S_{i,j}$
, it follows that
$S_i = \bigcap _{j>i} S_{i,j}$
, it follows that
![]() $S_i$
must be the
$S_i$
must be the
![]() $1$
-simplex spanned by
$1$
-simplex spanned by
![]() $p_i$
and
$p_i$
and
![]() $q_i$
. This proves the Proposition.
$q_i$
. This proves the Proposition.
Recall the unfolding sequence
![]() $(\tau _i)_{i \ge 0}$
, where
$(\tau _i)_{i \ge 0}$
, where
![]() $M_{r_i}$
is the transition matrix of the train track map
$M_{r_i}$
is the transition matrix of the train track map
![]() $\phi _{r_i}: \tau _i \to \tau _{i-1}$
. Let
$\phi _{r_i}: \tau _i \to \tau _{i-1}$
. Let
![]() $\Lambda $
be the legal lamination of
$\Lambda $
be the legal lamination of
![]() $(\tau _i)_{i \ge 0}$
.
$(\tau _i)_{i \ge 0}$
.
Corollary 6.4. If
![]() $(r_i)_{i \ge 1}$
is a positive sequence with
$(r_i)_{i \ge 1}$
is a positive sequence with
![]() $r_{i+1}-r_i \ge i$
, then
$r_{i+1}-r_i \ge i$
, then
![]() ${\mathbb P}\text {Curr}(\Lambda )$
is a 1-simplex.
${\mathbb P}\text {Curr}(\Lambda )$
is a 1-simplex.
Proof. In light of Theorem 3.3, it is enough to show
![]() ${\mathbb P}\text {Curr}((\tau _i)_i)$
is a 1-simplex. For each
${\mathbb P}\text {Curr}((\tau _i)_i)$
is a 1-simplex. For each
![]() $i \ge 0$
, we have a well-defined projection
$i \ge 0$
, we have a well-defined projection
The image of the projection is
![]() $S_{i+1}$
, which is always a
$S_{i+1}$
, which is always a
![]() $1$
-simplex by Proposition 6.1. Therefore,
$1$
-simplex by Proposition 6.1. Therefore,
![]() ${\mathbb P}\text {Curr}((\tau _i)_i)$
is a
${\mathbb P}\text {Curr}((\tau _i)_i)$
is a
![]() $1$
-simplex.
$1$
-simplex.
7. Nonuniquely ergometric tree
The goal of this section is to show that if a sequence
![]() $(r_i)_{i \ge 1}$
grows sufficiently fast, then the set of projectivized length measures
$(r_i)_{i \ge 1}$
grows sufficiently fast, then the set of projectivized length measures
![]() ${\mathbb P}{\mathcal D}((\tau _i')_i)$
on the folding sequence
${\mathbb P}{\mathcal D}((\tau _i')_i)$
on the folding sequence
![]() $(\tau _i')_i)$
is a 1-simplex. By Proposition 3.1, if
$(\tau _i')_i)$
is a 1-simplex. By Proposition 3.1, if
![]() $(\tau _i')_i$
converges to an arational tree T, then
$(\tau _i')_i$
converges to an arational tree T, then
![]() ${\mathbb P}{\mathcal D}(T)$
is also a 1-simplex in
${\mathbb P}{\mathcal D}(T)$
is also a 1-simplex in
![]() $\partial {\text {CV}_{7}}$
.
$\partial {\text {CV}_{7}}$
.
Recall that
![]() $N_r$
is a
$N_r$
is a
![]() $7\times 7$
matrix of the block form
$7\times 7$
matrix of the block form
 $$\begin{align*}\begin{pmatrix} 0&C^r\\ I&0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0&C^r\\ I&0 \end{pmatrix}, \end{align*}$$
where I is the
![]() $4\times 4$
identity matrix, and C is the transition matrix of
$4\times 4$
identity matrix, and C is the transition matrix of
![]() $\vartheta $
. The transpose of
$\vartheta $
. The transpose of
![]() $N_r$
has the same shape as
$N_r$
has the same shape as
![]() $M_r$
. Therefore, the same theory from Section 6 holds true. For brevity, we record only the essential statements that will be used later and omit all proofs from this section.
$M_r$
. Therefore, the same theory from Section 6 holds true. For brevity, we record only the essential statements that will be used later and omit all proofs from this section.
Let
![]() $\lambda _C$
be the Perron–Frobenius eigenvalue of C. Let
$\lambda _C$
be the Perron–Frobenius eigenvalue of C. Let
![]() $\kappa _C$
be the constants of Lemma 4.6. Given a sequence
$\kappa _C$
be the constants of Lemma 4.6. Given a sequence
![]() $(r_i)_i$
, define for each
$(r_i)_i$
, define for each
![]() $i \ge 1$
$i \ge 1$
 $$\begin{align*}Q_i = \frac{1}{\kappa_C \lambda_C^{r_{i+1}}} N_{r_{i+1}} N_{r_i}. \end{align*}$$
$$\begin{align*}Q_i = \frac{1}{\kappa_C \lambda_C^{r_{i+1}}} N_{r_{i+1}} N_{r_i}. \end{align*}$$
Lemma 7.1. Given a sequence
![]() $(r_i)_{i \ge 1}$
of positive integers such that
$(r_i)_{i \ge 1}$
of positive integers such that
![]() $r_{i+1}-r_i \ge i$
. Then for all
$r_{i+1}-r_i \ge i$
. Then for all
![]() $i \ge 1$
, the sequence of matrices
$i \ge 1$
, the sequence of matrices
![]() $\{ Q_{i+2k}\cdots Q_{i+2} Q_i\}_{k=0}^\infty $
converges to a matrix
$\{ Q_{i+2k}\cdots Q_{i+2} Q_i\}_{k=0}^\infty $
converges to a matrix
![]() $Z_i$
. Furthermore,
$Z_i$
. Furthermore,
![]() $\lim _{i \to \infty } Z_i=Z$
, where Z is the idempotent matrix of Lemma 4.6.
$\lim _{i \to \infty } Z_i=Z$
, where Z is the idempotent matrix of Lemma 4.6.
Corollary 7.2. If
![]() $(r_i)_{i \ge 1}$
is a positive sequence with
$(r_i)_{i \ge 1}$
is a positive sequence with
![]() $r_{i+1}-r_i \ge i$
, then
$r_{i+1}-r_i \ge i$
, then
![]() ${\mathbb P}{\mathcal D}((\tau _i')_i)$
, and hence
${\mathbb P}{\mathcal D}((\tau _i')_i)$
, and hence
![]() ${\mathbb P}{\mathcal D}(T)$
, is a 1-simplex.
${\mathbb P}{\mathcal D}(T)$
, is a 1-simplex.
8. Nonuniquely ergodic tree
In this section, we relate the legal lamination
![]() $\Lambda $
associated to the unfolding sequence
$\Lambda $
associated to the unfolding sequence
![]() $(\tau _i)_i$
defined in Section 6 and the limiting tree T of the folding sequence
$(\tau _i)_i$
defined in Section 6 and the limiting tree T of the folding sequence
![]() $(\tau _i')_i$
defined in Section 5, to show that T is not uniquely ergodic.
$(\tau _i')_i$
defined in Section 5, to show that T is not uniquely ergodic.
Recall the automorphism
![]() $\Phi _i = \phi _{r_1} \circ \cdots \phi _{r_i}$
, with
$\Phi _i = \phi _{r_1} \circ \cdots \phi _{r_i}$
, with
![]() $\Phi _0 = \operatorname {\mathrm {id}}$
. We also use
$\Phi _0 = \operatorname {\mathrm {id}}$
. We also use
![]() $\Phi _i$
to denote the induced graph map from
$\Phi _i$
to denote the induced graph map from
![]() $\tau _i$
to
$\tau _i$
to
![]() $\tau _0$
. If each
$\tau _0$
. If each
![]() $\tau _i$
and
$\tau _i$
and
![]() $\tau _i'$
as a marked graph is the rose labeled by
$\tau _i'$
as a marked graph is the rose labeled by
![]() $\{a_i, b_i, c_i, d_i, e_i, f_i, g_i\}$
, then
$\{a_i, b_i, c_i, d_i, e_i, f_i, g_i\}$
, then
![]() $x_i$
is represented by
$x_i$
is represented by
![]() $\Phi _i(x)$
for
$\Phi _i(x)$
for
![]() $x \in \{a,b,c,d,e,f,g\}$
as a word in
$x \in \{a,b,c,d,e,f,g\}$
as a word in
![]() ${\mathbb {F}_{7}} = \langle a,b,c,d,e,f,g\rangle = \pi _1(\tau _0) = \pi _1(\tau _0')$
. We denote
${\mathbb {F}_{7}} = \langle a,b,c,d,e,f,g\rangle = \pi _1(\tau _0) = \pi _1(\tau _0')$
. We denote
![]() $x_0$
as above simply by x.
$x_0$
as above simply by x.
Lemma 8.1. If
![]() $(r_i)_{i \ge 1}$
is positive, then for any length measure
$(r_i)_{i \ge 1}$
is positive, then for any length measure
![]() $(\lambda _i)_i \in {\mathcal D}((\tau ^{\prime }_i)_i)$
, the
$(\lambda _i)_i \in {\mathcal D}((\tau ^{\prime }_i)_i)$
, the
![]() $\lambda _i$
-volume of
$\lambda _i$
-volume of
![]() $\tau _i'$
goes to
$\tau _i'$
goes to
![]() $0$
as
$0$
as
![]() $i \to \infty $
.
$i \to \infty $
.
Proof. The composition
![]() $\psi _{r_i}\psi _{r_{i-1}}\psi _{r_{i-2}}:\tau _{i-3}'\to \tau _i'$
has the property that the preimage of every point of
$\psi _{r_i}\psi _{r_{i-1}}\psi _{r_{i-2}}:\tau _{i-3}'\to \tau _i'$
has the property that the preimage of every point of
![]() $\tau _i'$
consists of at least two (in fact, many more) points of
$\tau _i'$
consists of at least two (in fact, many more) points of
![]() $\tau _{i-3}'$
, and so the
$\tau _{i-3}'$
, and so the
![]() $\lambda _i$
-volume of
$\lambda _i$
-volume of
![]() $\tau _i'$
is at most half of the
$\tau _i'$
is at most half of the
![]() $\lambda _{i-3}$
-volume of
$\lambda _{i-3}$
-volume of
![]() $\tau _{i-3}'$
.
$\tau _{i-3}'$
.
Lemma 8.2. Suppose
![]() $(r_i)_{i \ge 1}$
is positive. Let
$(r_i)_{i \ge 1}$
is positive. Let
![]() $\Lambda $
be the legal lamination of the unfolding sequence
$\Lambda $
be the legal lamination of the unfolding sequence
![]() $(\tau _i)_i$
. Then every leaf in
$(\tau _i)_i$
. Then every leaf in
![]() $\Lambda $
is obtained as a limit of a sequence
$\Lambda $
is obtained as a limit of a sequence
![]() $\{\Phi _i(w)\}_i$
, where w is a legal word in
$\{\Phi _i(w)\}_i$
, where w is a legal word in
![]() $\tau _0$
of length at most two in
$\tau _0$
of length at most two in
![]() $\{a, b, c, d, e, f, g\}$
and their inverses. Moreover, w can be closed up to a legal loop which is a cyclic word of length
$\{a, b, c, d, e, f, g\}$
and their inverses. Moreover, w can be closed up to a legal loop which is a cyclic word of length
![]() $\leq 3$
.
$\leq 3$
.
Proof. Let l be a leaf of
![]() $\Lambda $
realized as a bi-infinite line in
$\Lambda $
realized as a bi-infinite line in
![]() $\tau _0$
, and let s be any subsegment of l, with combinatorial edge length
$\tau _0$
, and let s be any subsegment of l, with combinatorial edge length
![]() $\ell _s>0$
in
$\ell _s>0$
in
![]() $\tau _0$
. By definition, for every i there is a bi-infinite legal path
$\tau _0$
. By definition, for every i there is a bi-infinite legal path
![]() $l_i$
in
$l_i$
in
![]() $\tau _i$
such that
$\tau _i$
such that
![]() $l = \Phi _i(l_i)$
. Let
$l = \Phi _i(l_i)$
. Let
![]() $i = i(s) \geq 0$
such that the edge length of
$i = i(s) \geq 0$
such that the edge length of
![]() $x_i$
in
$x_i$
in
![]() $\tau _0$
under the graph map
$\tau _0$
under the graph map
![]() $\Phi _i$
is
$\Phi _i$
is
![]() $\geq \ell _s$
for all
$\geq \ell _s$
for all
![]() $x \in \{a, b, c, d, e, f, g\}$
. Thus, there is a segment
$x \in \{a, b, c, d, e, f, g\}$
. Thus, there is a segment
![]() $s_i$
of
$s_i$
of
![]() $l_i$
of combinatorial length at most two in
$l_i$
of combinatorial length at most two in
![]() $\{a_i, b_i , c_i, d_i, e_i, f_i, g_i\}$
such that
$\{a_i, b_i , c_i, d_i, e_i, f_i, g_i\}$
such that
![]() $s \subset \Phi _i(s_i)$
(here,
$s \subset \Phi _i(s_i)$
(here,
![]() $\Phi _i$
is a graph map). Now, if
$\Phi _i$
is a graph map). Now, if
![]() $s_i = x_iy_i$
for
$s_i = x_iy_i$
for
![]() $x, y \in \{a,b,c,d,e,f,g\}$
, take
$x, y \in \{a,b,c,d,e,f,g\}$
, take
![]() $w=xy$
. Thus, we see that
$w=xy$
. Thus, we see that
![]() $\Phi _i (w)$
(here,
$\Phi _i (w)$
(here,
![]() $\Phi _i$
is an automorphism) covers s in
$\Phi _i$
is an automorphism) covers s in
![]() $\tau _0$
. Since this is true for any segment of l, we conclude the lemma by taking a nested sequence of subsegments of l with edge length in
$\tau _0$
. Since this is true for any segment of l, we conclude the lemma by taking a nested sequence of subsegments of l with edge length in
![]() $\tau _0$
going to infinity. The fact that legal paths of length
$\tau _0$
going to infinity. The fact that legal paths of length
![]() $\leq 2$
can be closed up to legal loops of length
$\leq 2$
can be closed up to legal loops of length
![]() $\leq 3$
follows from the description of the train track in Lemma 4.3.
$\leq 3$
follows from the description of the train track in Lemma 4.3.
Recall that if
![]() $(\tau _i')_i$
converges to an arational tree T, then we can identify
$(\tau _i')_i$
converges to an arational tree T, then we can identify
![]() ${\mathcal D}((\tau _i')_i)$
with
${\mathcal D}((\tau _i')_i)$
with
![]() ${\mathcal D}(T)$
by Proposition 3.1.
${\mathcal D}(T)$
by Proposition 3.1.
Lemma 8.3. Suppose
![]() $(r_i)_{i \ge 1}$
is positive and that the folding sequence
$(r_i)_{i \ge 1}$
is positive and that the folding sequence
![]() $(\tau _i')_i$
converges to an arational tree T. Let w be any conjugacy class in
$(\tau _i')_i$
converges to an arational tree T. Let w be any conjugacy class in
![]() $\mathbb F_7$
represented by a cyclic word in
$\mathbb F_7$
represented by a cyclic word in
![]() $\{a,b,c,d,e,f,g\}$
and their inverses, and let
$\{a,b,c,d,e,f,g\}$
and their inverses, and let
![]() $\lambda \in {\mathcal D}(T)$
correspond to a length measure
$\lambda \in {\mathcal D}(T)$
correspond to a length measure
![]() $(\lambda _i)_i \in {\mathcal D}((\tau _i')_i)$
. Then
$(\lambda _i)_i \in {\mathcal D}((\tau _i')_i)$
. Then
Proof. Under the isomorphism from
![]() ${\mathcal D}((\tau _i')_i) \to {\mathcal D}(T)$
that maps
${\mathcal D}((\tau _i')_i) \to {\mathcal D}(T)$
that maps
![]() $(\lambda _i)_i \mapsto \lambda $
, the sequence
$(\lambda _i)_i \mapsto \lambda $
, the sequence
![]() $(\tau _i',\lambda _i) \subset {\text {cv}_{7}}$
also converges to
$(\tau _i',\lambda _i) \subset {\text {cv}_{7}}$
also converges to
![]() $(T,\lambda ) \in \partial {\text {cv}_{7}}$
. Thus, for any
$(T,\lambda ) \in \partial {\text {cv}_{7}}$
. Thus, for any
![]() $x \in {\mathbb {F}_{7}}$
,
$x \in {\mathbb {F}_{7}}$
,
In fact, the sequence
![]() $\left \lVert x\right \rVert _{(\tau _i', \lambda _i)}$
is monotonically nonincreasing. Recall that
$\left \lVert x\right \rVert _{(\tau _i', \lambda _i)}$
is monotonically nonincreasing. Recall that
![]() $\tau _0'$
as a marked graph is the rose labeled by
$\tau _0'$
as a marked graph is the rose labeled by
![]() $\{a,b,c,d,e,f,g\}$
. Represent w by a loop
$\{a,b,c,d,e,f,g\}$
. Represent w by a loop
![]() $c_w$
in
$c_w$
in
![]() $\tau _0'$
. The graph
$\tau _0'$
. The graph
![]() $\tau _i'$
is the rose labeled by
$\tau _i'$
is the rose labeled by
![]() $\{\Phi _i(a),\ldots ,\Phi _i(g)\}$
. Thus, the loop
$\{\Phi _i(a),\ldots ,\Phi _i(g)\}$
. Thus, the loop
![]() $c_w$
in
$c_w$
in
![]() $\tau _i'$
represents the conjugacy class
$\tau _i'$
represents the conjugacy class
![]() $\Phi _{i}(w)$
. This shows
$\Phi _{i}(w)$
. This shows
where
![]() $\left \lVert w\right \rVert _{\mbox {word}}$
is the word length of w. By Lemma 8.1, the last term goes to 0.
$\left \lVert w\right \rVert _{\mbox {word}}$
is the word length of w. By Lemma 8.1, the last term goes to 0.
We now come to the main statement of this section.
Proposition 8.4. Suppose
![]() $(r_i)_{i \ge 1}$
is positive and that the folding sequence
$(r_i)_{i \ge 1}$
is positive and that the folding sequence
![]() $(\tau _i')_i$
converges to an arational tree T. Let
$(\tau _i')_i$
converges to an arational tree T. Let
![]() $\tilde {\Lambda }$
be the lamination corresponding to the legal lamination
$\tilde {\Lambda }$
be the lamination corresponding to the legal lamination
![]() $\Lambda $
of the unfolding sequence
$\Lambda $
of the unfolding sequence
![]() $(\tau _i)_i$
, and let
$(\tau _i)_i$
, and let
![]() $L(T)$
be the lamination dual to T. Then
$L(T)$
be the lamination dual to T. Then
![]() $\tilde {\Lambda } \subseteq L(T)$
. In particular, if T is nongeometric, then
$\tilde {\Lambda } \subseteq L(T)$
. In particular, if T is nongeometric, then
![]() $\text {Curr}(\Lambda ) = \text {Curr}(T)$
.
$\text {Curr}(\Lambda ) = \text {Curr}(T)$
.
Proof. Recall by Lemma 2.4, the lamination dual to an arational tree is independent of the length measure on the tree. So fix an arbitrary length measure
![]() $\lambda \in {\mathcal D}(T)$
on T.
$\lambda \in {\mathcal D}(T)$
on T.
Let
![]() $W_3$
be the set of legal loops of length at most three in
$W_3$
be the set of legal loops of length at most three in
![]() $\{a, b, c, d, e, f, g\}$
and their inverses. By Lemma 8.3, for every
$\{a, b, c, d, e, f, g\}$
and their inverses. By Lemma 8.3, for every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $I_\epsilon>0$
such that for all
$I_\epsilon>0$
such that for all
![]() $i \geq I_\epsilon $
,
$i \geq I_\epsilon $
,
![]() $\left \lVert \Phi _i(w)_{(T,\lambda )}\right \rVert < \epsilon $
, for every
$\left \lVert \Phi _i(w)_{(T,\lambda )}\right \rVert < \epsilon $
, for every
![]() $ w\in W_3$
. Then the bi-infinite line
$ w\in W_3$
. Then the bi-infinite line
![]() $(\Phi _i(w)^{-\infty }, \Phi _i(w)^{\infty })$
is in
$(\Phi _i(w)^{-\infty }, \Phi _i(w)^{\infty })$
is in
![]() $L_{\epsilon }(T)$
for all
$L_{\epsilon }(T)$
for all
![]() $i \geq I_{\epsilon }$
. Therefore,
$i \geq I_{\epsilon }$
. Therefore,
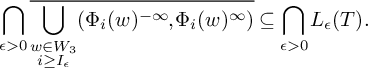 $$ \begin{align*}\bigcap_{\epsilon> 0} \overline{\bigcup_{\substack{w \in W_3 \\ i \geq I_{\epsilon}}} (\Phi_i(w)^{-\infty}, \Phi_i(w)^{\infty})} \subseteq \bigcap_{\epsilon > 0} L_{\epsilon}(T).\end{align*} $$
$$ \begin{align*}\bigcap_{\epsilon> 0} \overline{\bigcup_{\substack{w \in W_3 \\ i \geq I_{\epsilon}}} (\Phi_i(w)^{-\infty}, \Phi_i(w)^{\infty})} \subseteq \bigcap_{\epsilon > 0} L_{\epsilon}(T).\end{align*} $$
By Lemma 8.2, we conclude that
![]() $\tilde {\Lambda } \subseteq L(T)$
.
$\tilde {\Lambda } \subseteq L(T)$
.
If T is nongeometric and arational, then it is freely indecomposable by [Reference ReynoldsRey12]. By [Reference Coulbois, Hilion and ReynoldsCHR15, Corollary 1.4],
![]() $\text {Curr}(\Lambda ) = \text {Curr}(T)$
.
$\text {Curr}(\Lambda ) = \text {Curr}(T)$
.
The following is the consequence of Proposition 8.4 and Corollary 6.4.
Corollary 8.5. For a positive sequence
![]() $(r_i)_{i \ge 1}$
of integers with
$(r_i)_{i \ge 1}$
of integers with
![]() $r_{i+1}-r_i \ge i$
, if the folding sequence
$r_{i+1}-r_i \ge i$
, if the folding sequence
![]() $(\tau _i')_i$
converges to a nongeometric arational tree T, then
$(\tau _i')_i$
converges to a nongeometric arational tree T, then
![]() ${\mathbb P}\text {Curr}(T)$
is a 1-simplex. In particular, T is not uniquely ergodic.
${\mathbb P}\text {Curr}(T)$
is a 1-simplex. In particular, T is not uniquely ergodic.
9. Nonconvergence of unfolding sequence
In this section, fix a sequence
![]() $(r_i)_{i \ge 1}$
such that
$(r_i)_{i \ge 1}$
such that
![]() $r_{i+1}-r_i \ge i$
. We will show that the corresponding unfolding sequence
$r_{i+1}-r_i \ge i$
. We will show that the corresponding unfolding sequence
![]() $(\tau _i)_i$
does not converge to a unique point in
$(\tau _i)_i$
does not converge to a unique point in
![]() $\partial {\text {CV}_{7}}$
. In fact, we will show in Corollary 9.3 that it converges to a 1-simplex in
$\partial {\text {CV}_{7}}$
. In fact, we will show in Corollary 9.3 that it converges to a 1-simplex in
![]() $\partial {\text {CV}_{7}}$
.
$\partial {\text {CV}_{7}}$
.
Recall the folding and unfolding sequences
![]() $(\tau _i')_i$
and
$(\tau _i')_i$
and
![]() $(\tau _i)_i$
, respectively, from Section 4.
$(\tau _i)_i$
, respectively, from Section 4.


Here,
![]() $\tau _i$
and
$\tau _i$
and
![]() $\tau _i'$
as marked graphs belong to the same simplex in
$\tau _i'$
as marked graphs belong to the same simplex in
![]() ${\text {CV}_{7}}$
. Also, recall the matrices defined for all
${\text {CV}_{7}}$
. Also, recall the matrices defined for all
![]() $i\ge 0$
$i\ge 0$
 $$\begin{align*}P_i = \frac{1}{\kappa_B \lambda_B^{r_{i+1} }} M_{r_i} M_{r_{i+1}} \qquad \text{and} \qquad Q_i = \frac{1}{\kappa_C \lambda_C^{r_{i+1} }} N_{r_{i+1}}N_{r_i},\end{align*}$$
$$\begin{align*}P_i = \frac{1}{\kappa_B \lambda_B^{r_{i+1} }} M_{r_i} M_{r_{i+1}} \qquad \text{and} \qquad Q_i = \frac{1}{\kappa_C \lambda_C^{r_{i+1} }} N_{r_{i+1}}N_{r_i},\end{align*}$$
and the existence of the limiting matrices from Lemma 6.3 and Lemma 7.1
For all even
![]() $2m \ge 0$
,
$2m \ge 0$
,
Similarly, for all odd
![]() $2m+1 \ge 1$
, set
$2m+1 \ge 1$
, set
Let
![]() $\ell =\ell _0 \in {\mathbb R}^{|E\tau _0|}$
be a positive length vector on
$\ell =\ell _0 \in {\mathbb R}^{|E\tau _0|}$
be a positive length vector on
![]() $\tau _0$
. Then
$\tau _0$
. Then
![]() $\ell $
determines a length vector
$\ell $
determines a length vector
![]() $\ell _i$
on each
$\ell _i$
on each
![]() $\tau _i$
given by
$\tau _i$
given by
![]() $\ell _i = M_{r_i}^T \ldots M_{r_1}^T \ell \in {\mathbb R}^{|E\tau _i|}$
. We set
$\ell _i = M_{r_i}^T \ldots M_{r_1}^T \ell \in {\mathbb R}^{|E\tau _i|}$
. We set
![]() $\ell _e^T = \ell ^T Y_1$
and
$\ell _e^T = \ell ^T Y_1$
and
![]() $\ell _o^T = \ell ^T \frac {M_{r_1}}{\lambda _B^{r_1}}Y_2$
. Note that both
$\ell _o^T = \ell ^T \frac {M_{r_1}}{\lambda _B^{r_1}}Y_2$
. Note that both
![]() $\ell _e$
and
$\ell _e$
and
![]() $\ell _o$
are positive vectors. For
$\ell _o$
are positive vectors. For
![]() $\ell _e$
, this follows since
$\ell _e$
, this follows since
![]() $\ell $
is a positive vector and
$\ell $
is a positive vector and
![]() $Y_1$
is a nonnegative matrix. Similarly,
$Y_1$
is a nonnegative matrix. Similarly,
![]() $\ell ^T M_{r_1}$
is positive and
$\ell ^T M_{r_1}$
is positive and
![]() $Y_2$
is nonnegative, so
$Y_2$
is nonnegative, so
![]() $\ell _o$
is also positive.
$\ell _o$
is also positive.
We will show the sequence
![]() $(\tau _i, \ell _i)_i \subset {\text {CV}_{7}} $
, up to rescaling, does not have a unique limit in
$(\tau _i, \ell _i)_i \subset {\text {CV}_{7}} $
, up to rescaling, does not have a unique limit in
![]() $\partial {\text {CV}_{7}}$
. We start by showing the even sequence and the odd sequence do converge, up to scaling. More precisely:
$\partial {\text {CV}_{7}}$
. We start by showing the even sequence and the odd sequence do converge, up to scaling. More precisely:
Lemma 9.1. For any positive length vector
![]() $\ell =\ell _0$
on
$\ell =\ell _0$
on
![]() $\tau _0$
, the corresponding even sequence
$\tau _0$
, the corresponding even sequence
![]() $\left ( \tau _{2m}, \frac {\ell _{2m}}{c_{2m}} \right )$
and odd sequence
$\left ( \tau _{2m}, \frac {\ell _{2m}}{c_{2m}} \right )$
and odd sequence
![]() $\left ( \tau _{2m+1}, \frac {\ell _{2m+1}}{c_{2m+1}} \right )$
of metric graphs converge to two points
$\left ( \tau _{2m+1}, \frac {\ell _{2m+1}}{c_{2m+1}} \right )$
of metric graphs converge to two points
![]() $T_e$
and
$T_e$
and
![]() $T_o$
, respectively, in
$T_o$
, respectively, in
![]() $\partial {\text {CV}_{7}}$
. In fact, for any conjugacy class
$\partial {\text {CV}_{7}}$
. In fact, for any conjugacy class
![]() $x \in {\mathbb {F}_{7}}$
, there exists an index
$x \in {\mathbb {F}_{7}}$
, there exists an index
![]() $i_x \ge 0$
, a vector
$i_x \ge 0$
, a vector
![]() $v_x \in {\mathbb R}^{|E\tau _{i_x}'|}$
and matrices
$v_x \in {\mathbb R}^{|E\tau _{i_x}'|}$
and matrices
![]() $Y_x^e$
and
$Y_x^e$
and
![]() $Y_x^o$
such that
$Y_x^o$
such that
Proof. Let
![]() $x \in {\mathbb {F}_{7}}$
be a cyclically reduced representative of its conjugacy class. By Lemma 4.8, there exists
$x \in {\mathbb {F}_{7}}$
be a cyclically reduced representative of its conjugacy class. By Lemma 4.8, there exists
![]() $i \geq 0$
such that x is legal in
$i \geq 0$
such that x is legal in
![]() $\tau _{i}'$
. Let
$\tau _{i}'$
. Let
![]() $i_x$
be the smallest index among such i. Then we can represent x by a vector
$i_x$
be the smallest index among such i. Then we can represent x by a vector
![]() $v_x$
in
$v_x$
in
![]() ${\mathbb R}^{|E\tau _{i_x}'|}$
and by the vector
${\mathbb R}^{|E\tau _{i_x}'|}$
and by the vector
![]() $N_{r_i}\ldots N_{{i_x+1}} v_{x}$
in
$N_{r_i}\ldots N_{{i_x+1}} v_{x}$
in
![]() ${\mathbb R}^{|E\tau _i|}$
for
${\mathbb R}^{|E\tau _i|}$
for
![]() $i \geq i_x$
. Thus, for all
$i \geq i_x$
. Thus, for all
![]() $i \ge i_x$
, we have
$i \ge i_x$
, we have
If
![]() $i_x$
is even, then write
$i_x$
is even, then write
![]() $i_x = 2m_x$
, and set
$i_x = 2m_x$
, and set
If
![]() $i_x$
is odd, then write
$i_x$
is odd, then write
![]() $i_x = 2m_x+1$
, and set
$i_x = 2m_x+1$
, and set
First, suppose
![]() $i_x$
is even. Then for all even
$i_x$
is even. Then for all even
![]() $2m \ge i_x$
, we have
$2m \ge i_x$
, we have
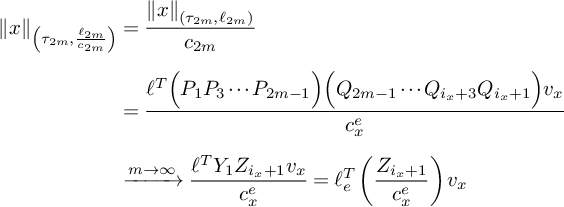 $$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m}, \frac{\ell_{2m}}{c_{2m}}\right)} & = \frac{\left\lVert x\right\rVert_{(\tau_{2m}, \ell_{2m})}}{c_{2m}} \\[.5em] & = \frac{\ell^T \Big(P_1 P_3 \cdots P_{2m-1} \Big) \Big( Q_{2m-1} \cdots Q_{i_x+3} Q_{i_x+1} \Big) v_x}{c_x^e} \\[.5em] &\xrightarrow{m \to \infty} \frac{\ell^T Y_1 Z_{i_x+1} v_x}{c_x^e} = \ell_e^T \left( \frac{Z_{i_x+1}}{c_x^e}\right) v_x \end{align*} $$
$$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m}, \frac{\ell_{2m}}{c_{2m}}\right)} & = \frac{\left\lVert x\right\rVert_{(\tau_{2m}, \ell_{2m})}}{c_{2m}} \\[.5em] & = \frac{\ell^T \Big(P_1 P_3 \cdots P_{2m-1} \Big) \Big( Q_{2m-1} \cdots Q_{i_x+3} Q_{i_x+1} \Big) v_x}{c_x^e} \\[.5em] &\xrightarrow{m \to \infty} \frac{\ell^T Y_1 Z_{i_x+1} v_x}{c_x^e} = \ell_e^T \left( \frac{Z_{i_x+1}}{c_x^e}\right) v_x \end{align*} $$
and for odd
![]() $2m+1 \ge i_x$
, we have
$2m+1 \ge i_x$
, we have
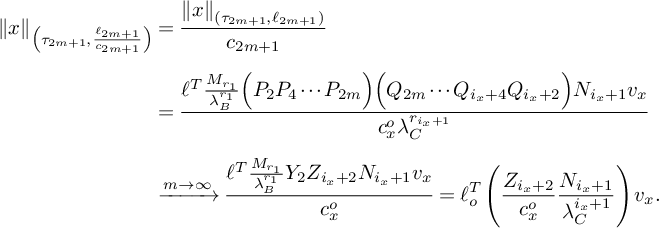 $$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m+1}, \frac{\ell_{2m+1}}{c_{2m+1}}\right)} & = \frac{\left\lVert x\right\rVert_{(\tau_{2m+1}, \ell_{2m+1})}}{c_{2m+1}} \\[.5em] & = \frac{\ell^T \frac{M_{r_1}}{\lambda_B^{r_1}} \Big( P_2 P_4 \cdots P_{2m} \Big) \Big( Q_{2m} \cdots Q_{i_x+4} Q_{i_x+2} \Big) N_{i_x+1} v_x}{c_x^o \lambda_C^{r_{i_x+1}}} \\[.5em] & \xrightarrow{m \to \infty} \frac{\ell^T \frac{M_{r_1}}{ \lambda_B^{r_1}} Y_2 Z_{i_x+2} N_{{i_x+1}} v_x }{c_x^o} = \ell_o^T \left(\frac{Z_{i_x+2}}{c_x^o}\frac{N_{{i_x+1}}}{ \lambda_C^{i_x+1}} \right) v_x. \end{align*} $$
$$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m+1}, \frac{\ell_{2m+1}}{c_{2m+1}}\right)} & = \frac{\left\lVert x\right\rVert_{(\tau_{2m+1}, \ell_{2m+1})}}{c_{2m+1}} \\[.5em] & = \frac{\ell^T \frac{M_{r_1}}{\lambda_B^{r_1}} \Big( P_2 P_4 \cdots P_{2m} \Big) \Big( Q_{2m} \cdots Q_{i_x+4} Q_{i_x+2} \Big) N_{i_x+1} v_x}{c_x^o \lambda_C^{r_{i_x+1}}} \\[.5em] & \xrightarrow{m \to \infty} \frac{\ell^T \frac{M_{r_1}}{ \lambda_B^{r_1}} Y_2 Z_{i_x+2} N_{{i_x+1}} v_x }{c_x^o} = \ell_o^T \left(\frac{Z_{i_x+2}}{c_x^o}\frac{N_{{i_x+1}}}{ \lambda_C^{i_x+1}} \right) v_x. \end{align*} $$
Now, suppose
![]() $i_x$
is odd. Then for all even
$i_x$
is odd. Then for all even
![]() $2m \ge i_x$
, we have
$2m \ge i_x$
, we have
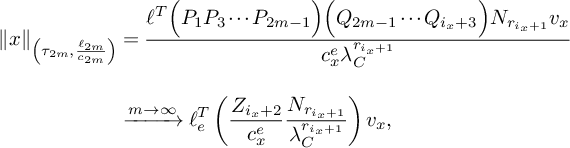 $$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m}, \frac{\ell_{2m}}{c_{2m}}\right)} & = \frac{\ell^T \Big(P_1 P_3\cdots P_{2m-1} \Big) \Big( Q_{2m-1} \cdots Q_{i_x+3} \Big) N_{r_{i_x+1}} v_x}{c_x^e \lambda_C^{r_{i_x+1}}} \\[1em] & \xrightarrow{m \to \infty} \ell_e^T \left( \frac{ Z_{i_x+2}}{c_x^e}\frac{N_{r_{i_x+1}}}{\lambda_C^{r_{i_x+1}}} \right) v_x, \end{align*} $$
$$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m}, \frac{\ell_{2m}}{c_{2m}}\right)} & = \frac{\ell^T \Big(P_1 P_3\cdots P_{2m-1} \Big) \Big( Q_{2m-1} \cdots Q_{i_x+3} \Big) N_{r_{i_x+1}} v_x}{c_x^e \lambda_C^{r_{i_x+1}}} \\[1em] & \xrightarrow{m \to \infty} \ell_e^T \left( \frac{ Z_{i_x+2}}{c_x^e}\frac{N_{r_{i_x+1}}}{\lambda_C^{r_{i_x+1}}} \right) v_x, \end{align*} $$
and for odd
![]() $2m+1 \ge i_x$
, we have
$2m+1 \ge i_x$
, we have
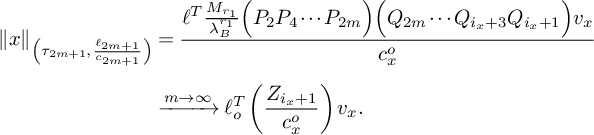 $$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m+1}, \frac{\ell_{2m+1}}{c_{2m+1}}\right)} & = \frac{\ell^T \frac{M_{r_1}}{\lambda_B^{r_1}} \Big( P_2 P_4 \cdots P_{2m} \Big) \Big( Q_{2m} \cdots Q_{i_x+3} Q_{i_x+1} \Big) v_x}{c_x^o} \\[.5em] & \xrightarrow{m \to \infty} \ell_o^T \left(\frac{Z_{i_x+1}}{c_x^o} \right) v_x. \end{align*} $$
$$ \begin{align*} \left\lVert x\right\rVert_{ \left( \tau_{2m+1}, \frac{\ell_{2m+1}}{c_{2m+1}}\right)} & = \frac{\ell^T \frac{M_{r_1}}{\lambda_B^{r_1}} \Big( P_2 P_4 \cdots P_{2m} \Big) \Big( Q_{2m} \cdots Q_{i_x+3} Q_{i_x+1} \Big) v_x}{c_x^o} \\[.5em] & \xrightarrow{m \to \infty} \ell_o^T \left(\frac{Z_{i_x+1}}{c_x^o} \right) v_x. \end{align*} $$
Either way, for any conjugacy class x in
![]() ${\mathbb {F}_{7}}$
, both
${\mathbb {F}_{7}}$
, both
are well defined and have the desired form.
We now want to show
![]() $T_e$
and
$T_e$
and
![]() $T_o$
are not scalar multiples of each other. In fact, the following lemma will allow us to show that
$T_o$
are not scalar multiples of each other. In fact, the following lemma will allow us to show that
![]() $T_e$
and
$T_e$
and
![]() $T_o$
are the extreme points of the simplex
$T_o$
are the extreme points of the simplex
![]() ${\mathbb P}{\mathcal D}(T)$
.
${\mathbb P}{\mathcal D}(T)$
.
Lemma 9.2. There exist two sequences
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
of conjugacy classes of elements of
$\beta _i$
of conjugacy classes of elements of
![]() ${\mathbb {F}_{7}}$
such that the following holds. For any positive length vector
${\mathbb {F}_{7}}$
such that the following holds. For any positive length vector
![]() $\ell =\ell _0$
on
$\ell =\ell _0$
on
![]() $\tau _0$
, let
$\tau _0$
, let
![]() $T_e$
and
$T_e$
and
![]() $T_o$
be the respective limiting trees in
$T_o$
be the respective limiting trees in
![]() $\partial {\text {CV}_{7}}$
for
$\partial {\text {CV}_{7}}$
for
![]() $\left ( \tau _{2m}, \frac {\ell _{2m}}{c_{2m}} \right )$
and
$\left ( \tau _{2m}, \frac {\ell _{2m}}{c_{2m}} \right )$
and
![]() $\left ( \tau _{2m+1}, \frac {\ell _{2m+1}}{c_{2m+1}} \right )$
. Then
$\left ( \tau _{2m+1}, \frac {\ell _{2m+1}}{c_{2m+1}} \right )$
. Then
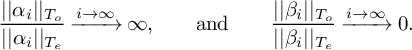 $$\begin{align*}\frac{||\alpha_i||_{T_o}}{||\alpha_i||_{T_e}} \xrightarrow{i \to \infty} \infty, \qquad \text{and} \qquad \frac{||\beta_i||_{T_o}}{||\beta_i||_{T_e}} \xrightarrow{i \to \infty} 0.\end{align*}$$
$$\begin{align*}\frac{||\alpha_i||_{T_o}}{||\alpha_i||_{T_e}} \xrightarrow{i \to \infty} \infty, \qquad \text{and} \qquad \frac{||\beta_i||_{T_o}}{||\beta_i||_{T_e}} \xrightarrow{i \to \infty} 0.\end{align*}$$
Proof. Take the letter
![]() $e \in {\mathbb {F}_{7}}$
and recall the automorphisms
$e \in {\mathbb {F}_{7}}$
and recall the automorphisms
![]() $\Phi _i$
used to define the folding and unfolding sequences. Set
$\Phi _i$
used to define the folding and unfolding sequences. Set
![]() $x_i = \Phi _i(e)$
. For each i,
$x_i = \Phi _i(e)$
. For each i,
![]() $x_i$
is legal in
$x_i$
is legal in
![]() $\tau _i'$
and is represented by the vector
$\tau _i'$
and is represented by the vector
![]() $e_5=(0,0,0,0,1,0,0)^T$
in
$e_5=(0,0,0,0,1,0,0)^T$
in
![]() $\tau _i'$
.
$\tau _i'$
.
Using notation from Lemma 9.1, set
![]() $c_{i}^e = c_{x_i}^e$
and
$c_{i}^e = c_{x_i}^e$
and
![]() $c_{i}^o = c_{x_i}^e$
. Note here i is the smallest index such that
$c_{i}^o = c_{x_i}^e$
. Note here i is the smallest index such that
![]() $x_i$
is legal in
$x_i$
is legal in
![]() $\tau _i'$
. We compare the ratio of
$\tau _i'$
. We compare the ratio of
![]() $c_i^o$
and
$c_i^o$
and
![]() $c_i^e$
. Since
$c_i^e$
. Since
![]() $r_{i+1} - r_i \to \infty $
, we have
$r_{i+1} - r_i \to \infty $
, we have
 $$\begin{align*}\frac{c_{2i}^e}{c_{2i}^o} = \frac{\lambda_C^{r_2} \cdots \lambda_C^{r_{2i}}} {\lambda_C^{r_1} \cdots \lambda_C^{r_{2i-1}}} \xrightarrow{i \to \infty} \infty, \qquad \text{while} \qquad \frac{c_{2i+1}^e}{c_{2i+1}^o} = \frac{\kappa_C}{\lambda_C^{r_1}} \frac{\lambda_C^{r_2} \cdots \lambda_C^{r_{2i}}} {\lambda_C^{r_3} \cdots \lambda_C^{r_{2i+1}}} \xrightarrow{i \to \infty} 0. \end{align*}$$
$$\begin{align*}\frac{c_{2i}^e}{c_{2i}^o} = \frac{\lambda_C^{r_2} \cdots \lambda_C^{r_{2i}}} {\lambda_C^{r_1} \cdots \lambda_C^{r_{2i-1}}} \xrightarrow{i \to \infty} \infty, \qquad \text{while} \qquad \frac{c_{2i+1}^e}{c_{2i+1}^o} = \frac{\kappa_C}{\lambda_C^{r_1}} \frac{\lambda_C^{r_2} \cdots \lambda_C^{r_{2i}}} {\lambda_C^{r_3} \cdots \lambda_C^{r_{2i+1}}} \xrightarrow{i \to \infty} 0. \end{align*}$$
Recall that both
![]() $\ell _e$
and
$\ell _e$
and
![]() $\ell _o$
are positive and by Lemma 7.1 the sequence
$\ell _o$
are positive and by Lemma 7.1 the sequence
![]() $Z_i $
converges to Z. Since
$Z_i $
converges to Z. Since
![]() $Ze_5$
is the zero vector, by continuity of the dot product,
$Ze_5$
is the zero vector, by continuity of the dot product,
Next, let
![]() $N_\infty = \lim _{i \to \infty } \frac {N_{r_i}}{ \lambda _C^{r_i}}$
and recall by Lemma 4.7 that the vector
$N_\infty = \lim _{i \to \infty } \frac {N_{r_i}}{ \lambda _C^{r_i}}$
and recall by Lemma 4.7 that the vector
![]() $Z N_\infty e_5=(\star ,\star ,\star, 0,0,0,0)$
is nonnegative. Thus, there are positive constants A and B such that
$Z N_\infty e_5=(\star ,\star ,\star, 0,0,0,0)$
is nonnegative. Thus, there are positive constants A and B such that
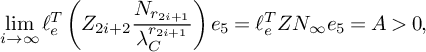 $$\begin{align*}\lim_{i \to \infty} \ell_e ^T \left (Z_{2i+2} \frac{N_{r_{2i+1}}}{\lambda_C^{r_{2i+1}}}\right ) e_5 = \ell_e^T ZN_\infty e_5 = A> 0, \end{align*}$$
$$\begin{align*}\lim_{i \to \infty} \ell_e ^T \left (Z_{2i+2} \frac{N_{r_{2i+1}}}{\lambda_C^{r_{2i+1}}}\right ) e_5 = \ell_e^T ZN_\infty e_5 = A> 0, \end{align*}$$
and
 $$\begin{align*}\lim_{i \to \infty} \ell_o^T \left(Z_{2i+2} \frac{N_{r_{2i+1}}}{ \lambda_C^{r_{2i+1}}}\right) e_5 = \ell_o^T Z N_\infty e_5 = B> 0.\end{align*}$$
$$\begin{align*}\lim_{i \to \infty} \ell_o^T \left(Z_{2i+2} \frac{N_{r_{2i+1}}}{ \lambda_C^{r_{2i+1}}}\right) e_5 = \ell_o^T Z N_\infty e_5 = B> 0.\end{align*}$$
Combining the above observations and the formulas for length of
![]() $x_i$
in
$x_i$
in
![]() $T_e$
and
$T_e$
and
![]() $T_o$
obtained in Lemma 9.1 we get
$T_o$
obtained in Lemma 9.1 we get
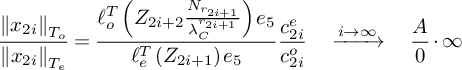 $$\begin{align*}\frac{\left\lVert x_{2i}\right\rVert_{T_o}}{\left\lVert x_{2i}\right\rVert_{T_e}} = \frac{\ell_o^T \left (Z_{2i+2} \frac{N_{r_{2i+1}}}{\lambda_C^{r_{2i+1}}}\right ) e_5}{\ell_e^T \left ( Z_{2i+1} \right ) e_5} \frac{c_{2i}^e}{c_{2i}^o} \quad \xrightarrow{i \to \infty} \quad \frac{A}{0} \cdot \infty \end{align*}$$
$$\begin{align*}\frac{\left\lVert x_{2i}\right\rVert_{T_o}}{\left\lVert x_{2i}\right\rVert_{T_e}} = \frac{\ell_o^T \left (Z_{2i+2} \frac{N_{r_{2i+1}}}{\lambda_C^{r_{2i+1}}}\right ) e_5}{\ell_e^T \left ( Z_{2i+1} \right ) e_5} \frac{c_{2i}^e}{c_{2i}^o} \quad \xrightarrow{i \to \infty} \quad \frac{A}{0} \cdot \infty \end{align*}$$
 $$\begin{align*}\frac{\left\lVert x_{2i+1}\right\rVert_{T_o}}{\left\lVert x_{2i+1}\right\rVert_{T_e}} = \frac{\ell_o^T \left ( Z_{2i+1} \right ) e_5}{\ell_e^T \left (Z_{2i+2} \frac{N_{r_{2i+1}}}{ \lambda_C^{r_{2i+1}}}\right ) e_5} \frac{c_{2i+1}^e}{c_{2i+1}^o} \quad \xrightarrow{i \to \infty} \quad \frac{0}{B} \cdot 0. \end{align*}$$
$$\begin{align*}\frac{\left\lVert x_{2i+1}\right\rVert_{T_o}}{\left\lVert x_{2i+1}\right\rVert_{T_e}} = \frac{\ell_o^T \left ( Z_{2i+1} \right ) e_5}{\ell_e^T \left (Z_{2i+2} \frac{N_{r_{2i+1}}}{ \lambda_C^{r_{2i+1}}}\right ) e_5} \frac{c_{2i+1}^e}{c_{2i+1}^o} \quad \xrightarrow{i \to \infty} \quad \frac{0}{B} \cdot 0. \end{align*}$$
Setting
![]() $\alpha _i = x_{2i}$
and
$\alpha _i = x_{2i}$
and
![]() $\beta _i= x_{2i+1}$
finishes the proof.
$\beta _i= x_{2i+1}$
finishes the proof.
Corollary 9.3. For a sequence
![]() $(r_i)_{i \ge 1}$
with
$(r_i)_{i \ge 1}$
with
![]() $r_{i+1}-r_i \ge i$
, if the folding sequence
$r_{i+1}-r_i \ge i$
, if the folding sequence
![]() $(\tau _i')_i$
converges to an arational tree T, then for any positive length vector
$(\tau _i')_i$
converges to an arational tree T, then for any positive length vector
![]() $\ell _0$
on
$\ell _0$
on
![]() $\tau _0$
, the limit set in
$\tau _0$
, the limit set in
![]() $\partial {\text {CV}_{7}}$
of the rescaled unfolding sequence
$\partial {\text {CV}_{7}}$
of the rescaled unfolding sequence
![]() $(\tau _i,\ell _i)$
is always the 1-simplex
$(\tau _i,\ell _i)$
is always the 1-simplex
![]() ${\mathbb P}{\mathcal D}(T)$
.
${\mathbb P}{\mathcal D}(T)$
.
Proof. Since the folding
![]() $(\tau _i)^{\prime }_i$
and the unfolding sequence
$(\tau _i)^{\prime }_i$
and the unfolding sequence
![]() $(\tau _i)_i$
are equal as marked graphs for all
$(\tau _i)_i$
are equal as marked graphs for all
![]() $i \ge 0$
, no matter the metric, they both visit the same sequence of simplices in
$i \ge 0$
, no matter the metric, they both visit the same sequence of simplices in
![]() ${\text {CV}_{7}}$
. In particular, they both project to the same quasigeodesic in
${\text {CV}_{7}}$
. In particular, they both project to the same quasigeodesic in
![]() ${\mathcal {FF}_{7}}$
. Thus, the two limiting trees
${\mathcal {FF}_{7}}$
. Thus, the two limiting trees
![]() $T_e$
and
$T_e$
and
![]() $T_o$
of the even and odd sequences of
$T_o$
of the even and odd sequences of
![]() $(\tau _i,\ell _i)$
are length measures on T.
$(\tau _i,\ell _i)$
are length measures on T.
Recall
![]() ${\mathbb P}{\mathcal D}(T)$
is a
${\mathbb P}{\mathcal D}(T)$
is a
![]() $1$
-simplex by Corollary 7.2. If neither
$1$
-simplex by Corollary 7.2. If neither
![]() $T_e$
nor
$T_e$
nor
![]() $T_o$
are the extreme points of this simplex, then there exist constants
$T_o$
are the extreme points of this simplex, then there exist constants
![]() $c, c'>0$
such that any
$c, c'>0$
such that any
![]() $x \in {\mathbb {F}_{n}}$
,
$x \in {\mathbb {F}_{n}}$
,
 $$\begin{align*}c'\leq \frac{\left\lVert x\right\rVert_{T_o}}{\left\lVert x\right\rVert_{T_e}} \leq c.\end{align*}$$
$$\begin{align*}c'\leq \frac{\left\lVert x\right\rVert_{T_o}}{\left\lVert x\right\rVert_{T_e}} \leq c.\end{align*}$$
On the other hand, if one of them, say
![]() $T_o$
, is an extreme point but
$T_o$
, is an extreme point but
![]() $T_e$
is not, then we have a constant
$T_e$
is not, then we have a constant
![]() $c>0$
such that for any
$c>0$
such that for any
![]() $x \in {\mathbb {F}_{n}}$
,
$x \in {\mathbb {F}_{n}}$
,
![]() $ \frac {\left \lVert x\right \rVert _{T_o}}{\left \lVert x\right \rVert _{T_e}} \leq c.$
In both the cases, we get a contradiction to Lemma 9.2.
$ \frac {\left \lVert x\right \rVert _{T_o}}{\left \lVert x\right \rVert _{T_e}} \leq c.$
In both the cases, we get a contradiction to Lemma 9.2.
10. Conclusion
Recall
![]() $\phi \in \operatorname {\mathrm {Aut}}({\mathbb {F}_{7}})$
is the automorphism
$\phi \in \operatorname {\mathrm {Aut}}({\mathbb {F}_{7}})$
is the automorphism
and
![]() $\rho \in \operatorname {\mathrm {Aut}}({\mathbb {F}_{7}})$
is the rotation by four clicks:
$\rho \in \operatorname {\mathrm {Aut}}({\mathbb {F}_{7}})$
is the rotation by four clicks:
For any integer r, let
![]() $\phi _r = \rho \phi ^r$
. To each sequence
$\phi _r = \rho \phi ^r$
. To each sequence
![]() $(r_i)_{i \ge 0}$
of positive integers, we have an unfolding sequence
$(r_i)_{i \ge 0}$
of positive integers, we have an unfolding sequence
![]() $(\tau _i)_i$
with train track map
$(\tau _i)_i$
with train track map
![]() $\phi _{r_i}\colon \, \tau _i \to \tau _{i-1}$
, and a folding sequence
$\phi _{r_i}\colon \, \tau _i \to \tau _{i-1}$
, and a folding sequence
![]() $(\tau _i')_i$
with train track map
$(\tau _i')_i$
with train track map
![]() $\phi _{r_i}^{-1}\colon \, \tau _{i-1}' \to \tau _i$
. By the limit set of the unfolding sequence
$\phi _{r_i}^{-1}\colon \, \tau _{i-1}' \to \tau _i$
. By the limit set of the unfolding sequence
![]() $(\tau _i)_i$
in
$(\tau _i)_i$
in
![]() $\partial {\text {CV}_{n}} $
we mean the limit set of
$\partial {\text {CV}_{n}} $
we mean the limit set of
![]() $(\tau _i,\ell _i)$
with respect to some (any) positive length vector
$(\tau _i,\ell _i)$
with respect to some (any) positive length vector
![]() $\ell _i$
on
$\ell _i$
on
![]() $\tau _i$
.
$\tau _i$
.
Main Theorem. Given a strictly increasing sequence
![]() $(r_i)_{i \geq 1}$
satisfying
$(r_i)_{i \geq 1}$
satisfying
![]() $r_i \equiv i \quad\mod 7$
and
$r_i \equiv i \quad\mod 7$
and
![]() $r_i \equiv 0 \quad\mod 3$
, then the folding sequence
$r_i \equiv 0 \quad\mod 3$
, then the folding sequence
![]() $(\tau ^{\prime }_i)_i$
converges to a nongeometric arational tree T.
$(\tau ^{\prime }_i)_i$
converges to a nongeometric arational tree T.
If
![]() $(r_i)_i$
grows fast enough, that is, if
$(r_i)_i$
grows fast enough, that is, if
![]() $r_{i+1}-r_i \ge i$
, then T is both nonuniquely ergometric and nonuniquely ergodic. Both
$r_{i+1}-r_i \ge i$
, then T is both nonuniquely ergometric and nonuniquely ergodic. Both
![]() ${\mathbb P}{\mathcal D}(T)$
and
${\mathbb P}{\mathcal D}(T)$
and
![]() ${\mathbb P}\text {Curr}(T)$
are one-dimensional simplices.
${\mathbb P}\text {Curr}(T)$
are one-dimensional simplices.
Furthermore, the limit set in
![]() $\partial {\text {CV}_{7}}$
of the unfolding sequence
$\partial {\text {CV}_{7}}$
of the unfolding sequence
![]() $(\tau _i)_i$
is always the 1-simplex spanned by the two ergodic metrics on T.
$(\tau _i)_i$
is always the 1-simplex spanned by the two ergodic metrics on T.
Proof. A sequence as in the statement exists by the Chinese remainder theorem. The first statement follows from Corollary 5.8 and Proposition 5.10. Nonunique ergometricity of T follows from Proposition 3.1 and Corollary 7.2. Nonunique ergodicity of T is Corollary 8.5. Finally, the last statement is Corollary 9.3.
A. Appendix
A.1. Convergence lemma
Let
![]() $\left \lVert \cdot \right \rVert $
denote the operator norm. Thus,
$\left \lVert \cdot \right \rVert $
denote the operator norm. Thus,
![]() $\left \lVert Y\right \rVert \geq 1$
for a nontrivial idempotent matrix Y.
$\left \lVert Y\right \rVert \geq 1$
for a nontrivial idempotent matrix Y.
Lemma A.1. Let Y be an idempotent matrix and
![]() $\Delta _i$
,
$\Delta _i$
,
![]() $i\geq 1$
, a sequence of matrices with
$i\geq 1$
, a sequence of matrices with
![]() $\left \lVert \Delta _i\right \rVert \leq \frac {\epsilon }{2^i}$
for some
$\left \lVert \Delta _i\right \rVert \leq \frac {\epsilon }{2^i}$
for some
![]() $\epsilon>0$
. Assume also that
$\epsilon>0$
. Assume also that
![]() $\epsilon \left \lVert Y\right \rVert \leq 1/2$
. Then the infinite product
$\epsilon \left \lVert Y\right \rVert \leq 1/2$
. Then the infinite product
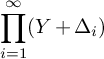 $$ \begin{align*}\prod_{i=1}^\infty (Y+\Delta_i)\end{align*} $$
$$ \begin{align*}\prod_{i=1}^\infty (Y+\Delta_i)\end{align*} $$
converges to a matrix X with
![]() $\left \lVert X-Y\right \rVert \leq 2\epsilon \Big (\left \lVert Y\right \rVert +\left \lVert Y\right \rVert ^2 \Big )$
. Moreover, the kernel of Y is contained in the kernel of X.
$\left \lVert X-Y\right \rVert \leq 2\epsilon \Big (\left \lVert Y\right \rVert +\left \lVert Y\right \rVert ^2 \Big )$
. Moreover, the kernel of Y is contained in the kernel of X.
Proof. Write
 $$ \begin{align*}Y+\Sigma_k=\prod_{i=1}^k (Y+\Delta_i)\end{align*} $$
$$ \begin{align*}Y+\Sigma_k=\prod_{i=1}^k (Y+\Delta_i)\end{align*} $$
Then
![]() $(Y+\Sigma _k)(Y+\Delta _{k+1})=Y+\Sigma _{k+1}$
and since
$(Y+\Sigma _k)(Y+\Delta _{k+1})=Y+\Sigma _{k+1}$
and since
![]() $Y^2=Y$
it follows that
$Y^2=Y$
it follows that
Multiplying on the right by Y and using
![]() $Y^2=Y$
, we get
$Y^2=Y$
, we get
and applying the norm
By adding these for
![]() $k=1,2,\cdots ,m-1$
and using
$k=1,2,\cdots ,m-1$
and using
![]() $\Sigma _1=\Delta _1$
, we have
$\Sigma _1=\Delta _1$
, we have
 $$ \begin{align*} \left\lVert\Sigma_mY\right\rVert & \leq \left\lVert\Sigma_1Y\right\rVert+\epsilon \left\lVert Y\right\rVert^2 \left(\frac 14+\cdots +\frac 1{2^m}\right)+\epsilon\left\lVert Y\right\rVert\left( \frac{\left\lVert\Sigma_1\right\rVert}{4}+\cdots+\frac{\left\lVert\Sigma_{m-1}\right\rVert}{2^m}\right) \\ & \leq \epsilon \Big( \left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \Big) + \epsilon\left\lVert Y\right\rVert\left( \frac{\left\lVert\Sigma_1\right\rVert}{4}+\cdots+\frac{\left\lVert\Sigma_{m-1}\right\rVert}{2^m} \right). \end{align*} $$
$$ \begin{align*} \left\lVert\Sigma_mY\right\rVert & \leq \left\lVert\Sigma_1Y\right\rVert+\epsilon \left\lVert Y\right\rVert^2 \left(\frac 14+\cdots +\frac 1{2^m}\right)+\epsilon\left\lVert Y\right\rVert\left( \frac{\left\lVert\Sigma_1\right\rVert}{4}+\cdots+\frac{\left\lVert\Sigma_{m-1}\right\rVert}{2^m}\right) \\ & \leq \epsilon \Big( \left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \Big) + \epsilon\left\lVert Y\right\rVert\left( \frac{\left\lVert\Sigma_1\right\rVert}{4}+\cdots+\frac{\left\lVert\Sigma_{m-1}\right\rVert}{2^m} \right). \end{align*} $$
So the norms of
![]() $\Sigma _mY$
are bounded by norms of
$\Sigma _mY$
are bounded by norms of
![]() $\Sigma _i$
with
$\Sigma _i$
with
![]() $i<m$
. From Equation 1, we also see that the norm of
$i<m$
. From Equation 1, we also see that the norm of
![]() $\Sigma _{k+1}$
is bounded by the norms of
$\Sigma _{k+1}$
is bounded by the norms of
![]() $\Sigma _kY$
. Putting this together, we have
$\Sigma _kY$
. Putting this together, we have
 $$ \begin{align*} \left\lVert\Sigma_{k+1}\right\rVert &\leq \left\lVert Y\right\rVert\left\lVert\Delta_{k+1}\right\rVert+\left\lVert\Sigma_kY\right\rVert+\left\lVert\Sigma_k\right\rVert\left\lVert\Delta_{k+1}\right\rVert\\ &\leq \frac{\epsilon}{2^{k+1}} \left\lVert Y\right\rVert + \left\lVert\Sigma_kY\right\rVert + \frac{\epsilon}{2^{k+1}} \left\lVert\Sigma_k\right\rVert\\ &\leq \frac{\epsilon}{2^{k+1}} \left\lVert Y\right\rVert + \frac{\epsilon}{2} \Big( \left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \Big) + \epsilon \left\lVert Y\right\rVert \left( \frac{\left\lVert\Sigma_1\right\rVert}{4} + \cdots + \frac{\left\lVert\Sigma_{k-1}\right\rVert}{2^k} \right) + \frac{\epsilon}{2^{k+1}} \left\lVert\Sigma_k\right\rVert \\ &\leq \epsilon \Big(\left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \Big) + \epsilon\left\lVert Y\right\rVert \left( \frac{\left\lVert\Sigma_1\right\rVert}{4}+\cdots+\frac{\left\lVert\Sigma_{k-1}\right\rVert}{2^k} + \frac{\left\lVert\Sigma_k\right\rVert}{2^{k+1}}\right). \end{align*} $$
$$ \begin{align*} \left\lVert\Sigma_{k+1}\right\rVert &\leq \left\lVert Y\right\rVert\left\lVert\Delta_{k+1}\right\rVert+\left\lVert\Sigma_kY\right\rVert+\left\lVert\Sigma_k\right\rVert\left\lVert\Delta_{k+1}\right\rVert\\ &\leq \frac{\epsilon}{2^{k+1}} \left\lVert Y\right\rVert + \left\lVert\Sigma_kY\right\rVert + \frac{\epsilon}{2^{k+1}} \left\lVert\Sigma_k\right\rVert\\ &\leq \frac{\epsilon}{2^{k+1}} \left\lVert Y\right\rVert + \frac{\epsilon}{2} \Big( \left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \Big) + \epsilon \left\lVert Y\right\rVert \left( \frac{\left\lVert\Sigma_1\right\rVert}{4} + \cdots + \frac{\left\lVert\Sigma_{k-1}\right\rVert}{2^k} \right) + \frac{\epsilon}{2^{k+1}} \left\lVert\Sigma_k\right\rVert \\ &\leq \epsilon \Big(\left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2 \Big) + \epsilon\left\lVert Y\right\rVert \left( \frac{\left\lVert\Sigma_1\right\rVert}{4}+\cdots+\frac{\left\lVert\Sigma_{k-1}\right\rVert}{2^k} + \frac{\left\lVert\Sigma_k\right\rVert}{2^{k+1}}\right). \end{align*} $$
Thus, we have an inequality of the form
 $$\begin{align*}\left\lVert\Sigma_{k+1}\right\rVert\leq a + b \left( \frac{\left\lVert\Sigma_1\right\rVert}{4} + \cdots + \frac{\left\lVert\Sigma_k\right\rVert}{2^{k+1}} \right) \end{align*}$$
$$\begin{align*}\left\lVert\Sigma_{k+1}\right\rVert\leq a + b \left( \frac{\left\lVert\Sigma_1\right\rVert}{4} + \cdots + \frac{\left\lVert\Sigma_k\right\rVert}{2^{k+1}} \right) \end{align*}$$
for
![]() $a = \epsilon \Big (\left \lVert Y\right \rVert + \left \lVert Y\right \rVert ^2 \Big )$
and
$a = \epsilon \Big (\left \lVert Y\right \rVert + \left \lVert Y\right \rVert ^2 \Big )$
and
![]() $b = \epsilon \left \lVert Y\right \rVert $
.
$b = \epsilon \left \lVert Y\right \rVert $
.
Set
![]() $c = 2 \epsilon \Big ( \left \lVert Y\right \rVert +\left \lVert Y\right \rVert ^2 \Big )$
. Then
$c = 2 \epsilon \Big ( \left \lVert Y\right \rVert +\left \lVert Y\right \rVert ^2 \Big )$
. Then
![]() $c \ge \epsilon $
,
$c \ge \epsilon $
,
![]() $a \le c/2$
and
$a \le c/2$
and
![]() $b \leq 1/2$
by assumption. Easy induction then shows for all
$b \leq 1/2$
by assumption. Easy induction then shows for all
![]() $k \ge 1$
,
$k \ge 1$
,
This obtains the inequality
![]() $\left \lVert X-Y\right \rVert \leq c$
from the statement, once we establish convergence.
$\left \lVert X-Y\right \rVert \leq c$
from the statement, once we establish convergence.
To see convergence, we argue that the sequence of partial products forms a Cauchy sequence. For
![]() $1<k<m$
,
$1<k<m$
,
 $$ \begin{align*} \prod_{i=1}^m (Y+\Delta_i) - \prod_{i=1}^k (Y+\Delta_i)= \prod_{i=1}^{k-1} (Y+\Delta_i) \bigg(\prod_{i=k}^m (Y+\Delta_i) - (Y+\Delta_k)\bigg). \end{align*} $$
$$ \begin{align*} \prod_{i=1}^m (Y+\Delta_i) - \prod_{i=1}^k (Y+\Delta_i)= \prod_{i=1}^{k-1} (Y+\Delta_i) \bigg(\prod_{i=k}^m (Y+\Delta_i) - (Y+\Delta_k)\bigg). \end{align*} $$
By Equation 2, the norm of
![]() $\prod _{i=1}^{k-1} (Y+\Delta _i) = Y + \Sigma _{k-1}$
is bounded by
$\prod _{i=1}^{k-1} (Y+\Delta _i) = Y + \Sigma _{k-1}$
is bounded by
![]() $c+\left \lVert Y\right \rVert $
. We can apply the same estimate to the sequence starting with
$c+\left \lVert Y\right \rVert $
. We can apply the same estimate to the sequence starting with
![]() $Y+\Delta _k$
and with
$Y+\Delta _k$
and with
![]() $\epsilon $
replaced with
$\epsilon $
replaced with
![]() $\frac {\epsilon }{2^{k-1}}$
to see that
$\frac {\epsilon }{2^{k-1}}$
to see that
 $$\begin{align*}\left\lVert\prod_{i=k}^m (Y+\Delta_i) - Y\right\rVert \leq \frac {2\epsilon(\left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2) }{2^{k-1}}\leq \frac {c}{2^{k-1}}\end{align*}$$
$$\begin{align*}\left\lVert\prod_{i=k}^m (Y+\Delta_i) - Y\right\rVert \leq \frac {2\epsilon(\left\lVert Y\right\rVert+\left\lVert Y\right\rVert^2) }{2^{k-1}}\leq \frac {c}{2^{k-1}}\end{align*}$$
and so
 $$\begin{align*}\left\lVert\prod_{i=k}^m (Y+\Delta_i) - (Y+\Delta_k)\right\rVert\leq \frac{c}{2^{k-1}}+ \frac{1}{2^k} \end{align*}$$
$$\begin{align*}\left\lVert\prod_{i=k}^m (Y+\Delta_i) - (Y+\Delta_k)\right\rVert\leq \frac{c}{2^{k-1}}+ \frac{1}{2^k} \end{align*}$$
which proves the sequence is Cauchy.
For the second statement, set
![]() $X_k = \prod _{i=k}^\infty (Y+\Delta _i)$
for
$X_k = \prod _{i=k}^\infty (Y+\Delta _i)$
for
![]() $k \ge 1$
. By the same estimate as above with
$k \ge 1$
. By the same estimate as above with
![]() $\epsilon $
replaced with
$\epsilon $
replaced with
![]() $\frac {\epsilon }{2^{k-1}}$
, we know that
$\frac {\epsilon }{2^{k-1}}$
, we know that
![]() $X_k$
exists and
$X_k$
exists and
By definition,
![]() $X = (Y+\Sigma _k)X_{k+1}$
. Suppose v is a unit vector with
$X = (Y+\Sigma _k)X_{k+1}$
. Suppose v is a unit vector with
![]() $Yv = 0$
. Then
$Yv = 0$
. Then
 $$ \begin{align*} \left\lVert Xv\right\rVert & \le \left\lVert Y+\Sigma_k\right\rVert \left\lVert X_{k+1} v\right\rVert \\ & = \left\lVert Y+\Sigma_k\right\rVert \left\lVert X_{k+1} v - Yv\right\rVert \\ & \le \left\lVert Y+\Sigma_k\right\rVert \left\lVert X_{k+1} - Y\right\rVert \\ & \le (\left\lVert Y\right\rVert+c) \frac{c}{2^k}. \end{align*} $$
$$ \begin{align*} \left\lVert Xv\right\rVert & \le \left\lVert Y+\Sigma_k\right\rVert \left\lVert X_{k+1} v\right\rVert \\ & = \left\lVert Y+\Sigma_k\right\rVert \left\lVert X_{k+1} v - Yv\right\rVert \\ & \le \left\lVert Y+\Sigma_k\right\rVert \left\lVert X_{k+1} - Y\right\rVert \\ & \le (\left\lVert Y\right\rVert+c) \frac{c}{2^k}. \end{align*} $$
Since this is true for all
![]() $k \ge 0$
, letting
$k \ge 0$
, letting
![]() $k \to \infty $
yields
$k \to \infty $
yields
![]() $X v = 0$
.
$X v = 0$
.
Acknowledgements
The authors gratefully acknowledge support: M.B. from NSF DMS-1905720, R.G. from the Sloan Foundation and J.T. from NSF DMS-1651963.
Competing interest
The authors have no competing interest to declare.