Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-20T10:25:44.118Z Has data issue: false hasContentIssue false
  • English
  • Français

KUMMER COVERINGS AND SPECIALISATION

Part of: Algebraic geometry: Foundations Families, fibrations

Published online by Cambridge University Press:  01 March 2021

Martin Olsson Open the ORCID record for Martin Olsson [Opens in a new window]
Martin Olsson*
Affiliation:
University of California, Berkeley, California, United States
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove versions of various classical results on specialisation of fundamental groups in the context of log schemes in the sense of Fontaine and Illusie, generalising earlier results of Hoshi, Lepage and Orgogozo. The key technical result relates the category of finite Kummer étale covers of an fs log scheme over a complete Noetherian local ring to the Kummer étale coverings of its reduction.

Keywords

log geometryfundamental groupstacks

MSC classification

Primary: 14A20: Generalizations (algebraic spaces, stacks) 14D06: Fibrations, degenerations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 1029 - 1065
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramovich, D., Olsson, M. and Vistoli, A., Tame stacks in positive characteristic, Ann. Inst. Fourier (Grenoble) 58 (2008), 1057–1091.CrossRefGoogle Scholar
Artin, M., Algebraic approximation of structures over complete local rings, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 23–58.CrossRefGoogle Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L., Théorie des topos et cohomologie étale des schémas, Lecture Notes in Math. 269, 270 and 305 (1972).Google Scholar
Borne, N. and Vistoli, A., Parabolic sheaves on logarithmic schemes, Adv. Math. 231 (2012), 1327–1363.Google Scholar
de Jong, A. J, Smoothness, semistability, and alterations, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93.CrossRefGoogle Scholar
Dieudonné, J. and Grothendieck, A., Eléments de géométrie algébrique, Publ. Math. Inst. Hautes Études Sci. 4, 8, 11, 17, 20, 24, 28 and 32 (1961–1967).Google Scholar
Emerton, M., ‘Formal algebraic stacks’, Preprint, undated, http://www.math.uchicago.edu/∼emerton/preprints.html.Google Scholar
Giraud, J., Cohomologie non abélienne, Grundlehren Math. Wiss. 179 (1971), ix+467 PP.CrossRefGoogle Scholar
Grothendieck, A., Revêtements étales et groupe fondamental, Lecture Notes in Math. 224 (1971), xviii+327 PP.CrossRefGoogle Scholar
Hoshi, Y., The exactness of the log homotopy sequence, Hiroshima Math. J. 39 (2009), 61–121.CrossRefGoogle Scholar
Illusie, L., An overview of the work of K. Fujiwara, K. Kato, and C. Nakayama on logarithmic étale cohomology, in Cohomologies $p$ -adiques et applications arithmétiques (II), Astérisque 279 (2002), 271–322.Google Scholar
Illusie, L., Kato, K. and Nakayama, C., Quasi-unipotent logarithmic Riemann-Hilbert correspondences, J. Math. Sci. Univ. Tokyo 12 (2005), 1–66.Google Scholar
Kato, K., Logarithmic structures of Fontaine-Illusie, in Algebraic Analysis, Geometry, and Number Theory (Baltimore, Johns Hopkins University Press, 1988), 191–224.Google Scholar
Kato, K., Toric singularities, Amer. J. Math. 116 (1994), 1073–1099.CrossRefGoogle Scholar
Laumon, G. and Moret-Bailly, L., Champs algébriques, Ergeb. Math. Grenzgeb. ( 3 ) 39 (2000), xii+208 PP.Google Scholar
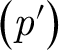Lepage, E., Covers in $p$ -adic analytic geometry and log covers I: cospecialization of the $\left({p}^{\prime}\right)$ -tempered fundamental group for a family of curves, Ann. Inst. Fourier (Grenoble) 63 (2013), 1427—1467.CrossRefGoogle Scholar
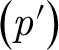Lepage, E., Covers in p-adic analytic geometry and log covers II: cospecialization of the $\left({p}^{\prime}\right)$ -tempered fundamental group in higher dimensions, Compos. Math. 148 (2012), 1443–1482.CrossRefGoogle Scholar
Mochizuki, S., Extending families of curves over log regular schemes, J. Reine Angew. Math. 511 (1999), 43–71.Google Scholar
Nakayama, C., Logarithmic étale cohomology, Math. Ann. 308 (1997), 365–404.CrossRefGoogle Scholar
Nakayama, C. and Ogus, A., Relative rounding in toric and logarithmic geometry, Geom. Topol. 14 (2010), 2189–2241.CrossRefGoogle Scholar
Ogus, A., Lectures on Logarithmic Algebraic Geometry , Cambridge Studies in Advanced Mathematics no. 178 (Cambridge University Press, 2018), xviii+539 PP.Google Scholar
Olsson, M., Hom–stacks and restriction of scalars, Duke Math. J. 134 (2006), 139–164.CrossRefGoogle Scholar
Olsson, M., Logarithmic geometry and algebraic stacks, Ann. Sci. Éc. Norm. Supér. (4) 36 (2003), 747–791.CrossRefGoogle Scholar
Orgogozo, F., Erratum et compléments à l’article Altérations et groupe fondamental premier á $p,\;$ paru au Bulletin de la S.M.F. (131), tome 1, Unpublished, 2003.CrossRefGoogle Scholar
Shiho, A., Crystalline fundamental groups. I. Isocrystals on log crystalline site and log convergent site, J. Math. Sci. Univ. Tokyo 7 (2000), 509–656.Google Scholar
The Stacks Project, 2017, http://stacks.math.columbia.edu.Google Scholar
Talpo, M. and Vistoli, A., Infinite root stacks and quasi-coherent sheaves on log schemes, Proc. Lond. Math. Soc. ( 3 ) 116 (2018), 1187—1243.CrossRefGoogle Scholar