Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T16:47:16.753Z Has data issue: false hasContentIssue false
  • English
  • Français

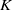$K$-theory of one-dimensional rings via pro-excision

Part of: Curves Higher algebraic $K$-theory

Published online by Cambridge University Press:  23 July 2013

Matthew Morrow
Matthew Morrow*
Affiliation:
University of Chicago, 5734 S. University Ave., Chicago, IL, 60637, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper studies ‘pro-excision’ for the 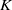$K$-theory of one-dimensional, usually semi-local, rings and its various applications. In particular, we prove Geller’s conjecture for equal characteristic rings over a perfect field of finite characteristic, give results towards Geller’s conjecture in mixed characteristic, and we establish various finiteness results for the 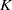$K$-groups of singularities, covering both orders in number fields and singular curves over finite fields.

Keywords

K-theoryexcisionsingularitiescyclic homologyp-adic fields

MSC classification

Secondary: 19D55: $K$-theory and homology; cyclic homology and cohomology 14H20: Singularities, local rings
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 2 , April 2014 , pp. 225 - 272
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, M. and Mazur, B., Etale homotopy, Lecture Notes in Mathematics, Volume 100 (Springer, Berlin, 1986). Reprint of the 1969 original.Google Scholar
Avramov, L. L. and Vigué-Poirrier, M., Hochschild homology criteria for smoothness, Int. Math. Res. Not. 1 (1992), 17–25.Google Scholar
Bloch, S., Algebraic $K$ -theory and crystalline cohomology, Publ. Math. Inst. Hautes Études Sci. 47 (1977), 187–268 (1978).CrossRefGoogle Scholar
Borel, A., Stable real cohomology of arithmetic groups, Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 235–272 (1975).CrossRefGoogle Scholar
Cathelineau, J.-L., $\lambda $ -structures in algebraic $K$ -theory and cyclic homology, K-Theory 4 6 (1990/91), 591–606.Google Scholar
Cohen, I. S., On the structure and ideal theory of complete local rings, Trans. Amer. Math. Soc. 59 (1946), 54–106.Google Scholar
Cortiñas, G., The obstruction to excision in $K$ -theory and in cyclic homology, Invent. Math. 164 1 (2006), 143–173.Google Scholar
Cortiñas, G., Geller, S. C. and Weibel, C. A., The Artinian Berger conjecture, Math. Z. 228 3 (1998), 569–588.CrossRefGoogle Scholar
Cortiñas, G., Haesemeyer, C. and Weibel, C. A., Infinitesimal cohomology and the Chern character to negative cyclic homology, Math. Ann. 344 4 (2009), 891–922.Google Scholar
Cortiñas, G. and Weibel, C., Relative Chern characters for nilpotent ideals, in Algebraic topology, Abel Symp., Volume 4, pp. 61–82 (Springer, Berlin, 2009).CrossRefGoogle Scholar
Davis, E. D., On the geometric interpretation of seminormality, Proc. Amer. Math. Soc. 68 1 (1978), 1–5.Google Scholar
Dennis, R. K. and Stein, M. R., ${K}_{2} $ of discrete valuation rings, Adv. Math. 18 2 (1975), 182–238.CrossRefGoogle Scholar
Gabber, O., $K$ -theory of Henselian local rings and Henselian pairs, in Algebraic K-theory, commutative algebra, and algebraic geometry (Santa Margherita Ligure, 1989), Contemp. Math., Volume 126, pp. 59–70 (Amer. Math. Soc, Providence, RI, 1992).Google Scholar
Geisser, T. and Hesselholt, L., Bi-relative algebraic $K$ -theory and topological cyclic homology, Invent. Math. 166 2 (2006), 359–395.CrossRefGoogle Scholar
Geisser, T. and Hesselholt, L., On relative and bi-relative algebraic $K$ -theory of rings of finite characteristic, J. Amer. Math. Soc. 24 1 (2011), 29–49.Google Scholar
Geller, S. C., A note on injectivity of lower $K$ -groups for integral domains, in Applications of algebraic K-theory to algebraic geometry and number theory, Part I, II (Boulder, Colo., 1983), Contemp. Math., Volume 55, pp. 437–447 (Amer. Math. Soc, Providence, RI, 1986). With an appendix by R. Keith Dennis and Clayton C. Sherman.Google Scholar
Geller, S., Reid, L. and Weibel, C., The cyclic homology and $K$ -theory of curves, J. Reine Angew. Math. 393 (1989), 39–90.Google Scholar
Goodwillie, T. G., Cyclic homology, derivations, and the free loopspace, Topology 24 2 (1985), 187–215.Google Scholar
Goodwillie, T. G., Relative algebraic $K$ -theory and cyclic homology, Ann. of Math. (2) 124 2 (1986), 347–402.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 231.Google Scholar
Harder, G., Die Kohomologie $S$ -arithmetischer Gruppen über Funktionenkörpern, Invent. Math. 42 (1977), 135–175.Google Scholar
Hesselholt, L., The tower of $K$ -theory of truncated polynomial algebras, J. Topol. 1 1 (2008), 87–114.Google Scholar
Hesselholt, L. and Madsen, I., Cyclic polytopes and the $K$ -theory of truncated polynomial algebras, Invent. Math. 130 1 (1997), 73–97.Google Scholar
Hesselholt, L. and Madsen, I., On the $K$ -theory of finite algebras over Witt vectors of perfect fields, Topology 36 1 (1997), 29–101.CrossRefGoogle Scholar
Hesselholt, L. and Madsen, I., On the $K$ -theory of nilpotent endomorphisms, in Homotopy methods in algebraic topology (Boulder, CO, 1999), Contemp. Math., Volume 271, pp. 127–140 (Amer. Math. Soc, Providence, RI, 2001).Google Scholar
Hesselholt, L. and Madsen, I., On the $K$ -theory of local fields, Ann. of Math. (2) 158 1 (2003), 1–113.Google Scholar
Huneke, C. and Swanson, I., Integral closure of ideals, rings, and modules, London Mathematical Society Lecture Note Series, Volume 336 (Cambridge University Press, Cambridge, 2006).Google Scholar
Illusie, L., Complexe de de Rham-Witt et cohomologie cristalline, Ann. Sci. Éc. Norm. Supér. (4) 12 4 (1979), 501–661.Google Scholar
Isaksen, D. C., Calculating limits and colimits in pro-categories, Fund. Math. 175 2 (2002), 175–194.CrossRefGoogle Scholar
Kato, K., A generalization of local class field theory by using $K$ -groups. II, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 27 3 (1980), 603–683.Google Scholar
Keune, F., The relativization of ${K}_{2} $ , J. Algebra 54 1 (1978), 159–177.Google Scholar
Krishna, A., On ${K}_{2} $ of one-dimensional local rings, K-Theory 35 1–2 (2005), 139–158.Google Scholar
Krishna, A., An Artin–Rees theorem in $K$ -theory and applications to zero cycles, J. Algebraic Geom. 19 3 (2010), 555–598.Google Scholar
Levine, M., The indecomposable ${K}_{3} $ of fields, Bull. Amer. Math. Soc. (N.S.) 17 2 (1987), 321–325.Google Scholar
Loday, J.-L., Cyclic homology, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 301 (Springer, Berlin, 1992). Appendix E by María O. Ronco.Google Scholar
Maazen, H. and Stienstra, J., A presentation for ${K}_{2} $ of split radical pairs, J. Pure Appl. Algebra 10 3 (1977/78), 271–294.Google Scholar
McCarthy, R., Relative algebraic $K$ -theory and topological cyclic homology, Acta Math. 179 2 (1997), 197–222.Google Scholar
Merkurjev, A. S., On the torsion in ${K}_{2} $ of local fields, Ann. of Math. (2) 118 2 (1983), 375–381.Google Scholar
Moore, C. C., Group extensions of $p$ -adic and adelic linear groups, Publ. Math. Inst. Hautes Études Sci. 35 (1968), 157–222.Google Scholar
Morrow, M., Pro excision and $cdh$ -descent for $K$ -theory, arXiv:1211.1813 (2012) (available at http://math.uchicago.edu/~mmorrow/).Google Scholar
Morrow, M., A singular analogue of Gersten’s conjecture and applications to $K$ -theoretic adèles, arXiv:1208.0931 (2012) (available at http://math.uchicago.edu/~mmorrow/).Google Scholar
Nesterenko, Y. P. and Suslin, A. A., Homology of the general linear group over a local ring, and Milnor’s $K$ -theory, Izv. Akad. Nauk SSSR Ser. Mat. 53 1 (1989), 121–146.Google Scholar
Panin, I. A., The equicharacteristic case of the Gersten conjecture, Tr. Mat. Inst. Steklova 241, Teor. Chisel, Algebra i Algebr. Geom. (2003), 169–178.Google Scholar
Popescu, D., General Néron desingularization, Nagoya Math. J. 100 (1985), 97–126.Google Scholar
Popescu, D., General Néron desingularization and approximation, Nagoya Math. J. 104 (1986), 85–115.CrossRefGoogle Scholar
Quillen, D., Finite generation of the groups ${K}_{i} $ of rings of algebraic integers, in Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), Lecture Notes in Math., Volume 341, pp. 179–198 (Springer, Berlin, 1973).Google Scholar
Roberts, L. G., The $K$ -theory of some reducible affine curves: a combinatorial approach, in Algebraic K-theory (Proc. Conf., Northwestern Univ., Evanston, Ill., 1976), Lecture Notes in Math., Volume 551, pp. 44–59 (Springer, Berlin, 1976).Google Scholar
Robinson, D. J. S., A course in the theory of groups, 2nd ed., Graduate Texts in Mathematics, Volume 80 (Springer, New York, 1996).Google Scholar
Sherman, C. C., The $K$ -theory of an equicharacteristic discrete valuation ring injects into the $K$ -theory of its field of quotients, Pacific J. Math. 74 2 (1978), 497–499.Google Scholar
Soulé, C., Groupes de Chow et $K$ -théorie de variétés sur un corps fini, Math. Ann. 268 3 (1984), 317–345.Google Scholar
Stienstra, J., Operations in the higher $K$ -theory of endomorphisms, in Current trends in algebraic topology, Part 1 (London, Ont., 1981), CMS Conf. Proc., Volume 2, pp. 59–115 (Amer. Math. Soc, Providence, RI, 1982).Google Scholar
Stienstra, J., Cartier–Dieudonné theory for Chow groups, J. Reine Angew. Math. 355 (1985), 1–66.Google Scholar
Suslin, A. A., On the $K$ -theory of local fields, in Proceedings of the Luminy conference on algebraic K-theory (Luminy, 1983), Volume 34, pp. 301–318 (1984).Google Scholar
Suslin, A. A., Excision in integer algebraic $K$ -theory, Trudy Mat. Inst. Steklov. 208, Teor. Chisel, Algebra i Algebr. Geom. (1995), 290–317. Dedicated to Academician Igor Rostislavovich Shafarevich on the occasion of his seventieth birthday (Russian).Google Scholar
Suslin, A. A. and Wodzicki, M., Excision in algebraic $K$ -theory, Ann. of Math. (2) 136 1 (1992), 51–122.CrossRefGoogle Scholar
Suslin, A. A. and Yufryakov, A. V., The $K$ -theory of local division algebras, Dokl. Akad. Nauk SSSR 288 4 (1986), 832–836.Google Scholar
Swan, R. G., Excision in algebraic $K$ -theory, J. Pure Appl. Algebra 1 3 (1971), 221–252.Google Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic $K$ -theory of schemes and of derived categories, in The Grothendieck Festschrift, Vol. III, Progr. Math., Volume 88, pp. 247–435 (Birkhäuser, Boston, MA, 1990).Google Scholar
Weibel, C. A., $K$ -theory and analytic isomorphisms, Invent. Math. 61 2 (1980), 177–197.Google Scholar
Weibel, C. A., ${K}_{2} , {K}_{3} $ and nilpotent ideals, J. Pure Appl. Algebra 18 3 (1980), 333–345.Google Scholar
Weibel, C. A., Mayer–Vietoris sequences and mod $p\hspace{0.167em} K$ -theory, in Algebraic K-theory, Part I (Oberwolfach, 1980), Lecture Notes in Math., Volume 966, pp. 390–407 (Springer, Berlin, 1982).Google Scholar
Weibel, C. A., $K$ -theory of 1-dimensional schemes, in Applications of algebraic K-theory to algebraic geometry and number theory, Part I, II (Boulder, Colo., 1983), Contemp. Math., Volume 55, pp. 811–818 (Amer. Math. Soc, Providence, RI, 1986).Google Scholar
Weibel, C. A., Homotopy algebraic $K$ -theory, in Algebraic K-theory and algebraic number theory (Honolulu, HI, 1987), Contemp. Math., Volume 83, pp. 461–488 (Amer. Math. Soc, Providence, RI, 1989).Google Scholar
Weibel, C. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, Volume 38 (Cambridge University Press, Cambridge, 1994).Google Scholar
Weibel, C., Algebraic $K$ -theory of rings of integers in local and global fields, in Handbook of K-theory, Vol. 1, 2, pp. 139–190 (Springer, Berlin, 2005).Google Scholar