Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T09:20:47.036Z Has data issue: false hasContentIssue false
  • English
  • Français

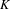$K$-THEORY OF MONOID ALGEBRAS AND A QUESTION OF GUBELADZE

Part of: (Co)homology theory Arithmetic rings and other special rings Higher algebraic $K$-theory

Published online by Cambridge University Press:  10 August 2017

Amalendu Krishna  and
Husney Parvez Sarwar
Amalendu Krishna
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, 1 Homi Bhabha Road, Colaba, Mumbai, India ([email protected]; [email protected])
Husney Parvez Sarwar
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, 1 Homi Bhabha Road, Colaba, Mumbai, India ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for any commutative Noetherian regular ring 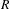$R$ containing 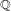$\mathbb{Q}$, the map 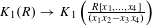$K_{1}(R)\rightarrow K_{1}\left(\frac{R[x_{1},\ldots ,x_{4}]}{(x_{1}x_{2}-x_{3}x_{4})}\right)$ is an isomorphism. This answers a question of Gubeladze. We also compute the higher 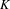$K$-theory of this monoid algebra. In particular, we show that the above isomorphism does not extend to all higher 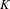$K$-groups. We give applications to a question of Lindel on the Serre dimension of monoid algebras.

Keywords

algebraic K-theorymonoid algebrassingular schemes

MSC classification

Primary: 19D50: Computations of higher $K$-theory of rings
Secondary: 13F15: Rings defined by factorization properties (e.g., atomic, factorial, half-factorial) 14F35: Homotopy theory; fundamental groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 5 , September 2019 , pp. 1051 - 1085
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, D. F., Projective modules over subrings of k[X, Y] generated by monomials, Pacific J. Math. 79 (1978), 5–17.Google Scholar
Artin, M. and Mazur, B., Etale Homotopy, Lecture Notes in Mathematics, Volume 100, xiv+461 pp. (Springer, Berlin–New York, 1969).Google Scholar
Bass, H., Algebraic K-Theory (W. A. Benjamin, Inc., New York-Amsterdam, 1968).Google Scholar
Bruns, W. and Gubeladze, J., Polytopes, Rings, and K-Theory, Springer Monographs in Mathematics, xiv+461 pp. (Springer, Dordrecht, 2009).Google Scholar
Cortiñas, G., Haesemeyer, C., Walker, M. and Weibel, C., K-theory of cones of smooth varieties, J. Algebraic Geom. 22 (2013), 13–34.Google Scholar
Cortiñas, G., Haesemeyer, C. and Weibel, C., K-regularity, cdh-fibrant Hochschild homology, and a conjecture of Vorst, J. Amer. Math. Soc. 21(2) (2008), 547–561.Google Scholar
Dhorajia, A. and Keshari, M., A note on cancellation of projective modules, J. Pure Appl. Algebra 216 (2012), 126–129.Google Scholar
Gracía-Sanchéz, P. A. and Rosales, J. C., Finitely Generated Commutative Monoids (Nova Sc. Publishers Inc., Commack, New York, 1999).Google Scholar
Gubeladze, J., Anderson’s conjecture and the maximal class of monoid over which projective modules are free, Math. USSR-Sb. 63 (1988), 165–188.Google Scholar
Gubeladze, J., Classical Algebraic K-Theory of Monoid Algebras, Lecture Notes in Mathematics, Volume 1437, pp. 36–94 (Springer, Berlin, 1990).Google Scholar
Gubeladze, J., Geometric and algebraic representations of commutative cancellative monoids, Proc. A. Razmadze Math. Inst. 113 (1995), 31–81.Google Scholar
Gubeladze, J., Nontriviality of SK 1(R[M]), J. Pure Appl. Algebra 104 (1995), 169–190.Google Scholar
Gubeladze, J., K-theory of affine toric varieties, Homology, Homotopy Appl. 1 (1999), 135–145.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Text in Mathematics, Volume 52 (Springer, New York, 1997).Google Scholar
Kang, M., Projective modules over some polynomial rings, J. Algebra 59 (1979), 65–76.Google Scholar
Kemf, G. R., Some elementary proofs of basic theorems in the cohomology of quasi-coherent sheaves, Rocky Mountain J. Math. 10(3) (1980), 637–646.Google Scholar
Keshari, M. and Sarwar, H. P., Serre dimension of monoid algebras, Proc. Math. Sci. Indian Acad. Sci. 127(2) (2017), 269–280.Google Scholar
Krishna, A., Zero cycles on a threefold with isolated singularities, J. Reine Angew. Math. 594 (2006), 93–115.Google Scholar
Krishna, A., An Artin–Rees theorem in K-theory and applications to zero cycles, J. Algebraic Geom. 19 (2010), 555–598.Google Scholar
Krishna, A. and Morrow, M., Analogues of Gersten’s conjecture for singular schemes, Selecta Math. (N.S.) 23 (2017), 1235–1247.Google Scholar
Krull, W., Dimensionstheorie in Stellenringen, J. Reine Angew. Math. 179 (1938), 204–226.Google Scholar
Lindel, H., Unimodular elements in projective modules, J. Algebra 172(2) (1995), 301–319.Google Scholar
Liu, Q., Algebraic Geometry and Arithmetic Curves, Oxford Graduate Text in Mathematics, Volume 6 (Oxford Science Publications, Oxford, 2002).Google Scholar
Loday, J.-L., Cyclic Homology, Grundlehern der Mathematischen Wissenschaften, Volume 301 (Springer, Berlin, 1992).Google Scholar
Matsumura, H., Commutative Ring Theory, Cambridge Studies in Advanced Mathematics, Volume 8 (Cambridge university press, Cambridge, 1997).Google Scholar
Morrow, M., Pro unitality and pro excision in algebraic K-theory and cyclic homology, J. Reine Angew. Math. (2015), to appear, https://arxiv.org/pdf/1404.4179.pdf.Google Scholar
Morrow, M., Pro cdh-descent for cyclic homology and K-theory, J. Inst. Math. Jussieu 15(3) (2016), 539–567.Google Scholar
Quillen, D., Higher algebraic K-theory I, Lect. Notes Math. 341 (1973), 85–147.Google Scholar
Roy, A., Application of patching diagrams to some questions about projective modules, J. Pure Appl. Algebra 24(3) (1982), 313–319.Google Scholar
Srinivas, V., K 1 of the cone over a curve, J. Reine Angew. Math. 381 (1987), 37–50.Google Scholar
Swan, R. G., Gubeladze’s proof of Anderson’s conjecture, Contemp. Math 124 (1992), 215–250.Google Scholar
Thomason, R. W. and Trobaugh, T., Higher Algebraic K-Theory Of Schemes And Of Derived Categories, The Grothendieck Festschrift III, Progress in Mathematics, Volume 88, pp. 247–435 (Birkhäuser, Boston, MA, 1990).Google Scholar
Vorst, T., Localization of the K-theory of polynomial extensions. With an appendix by Wilberd van der Kallen, Math. Ann. 244(1) (1979), 33–53.Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, Volume 38 (Cambridge University Press, Cambridge, 1994).Google Scholar
Weibel, C. A., Cyclic homology of Schemes, Proc. Amer. Math. Soc. 124 (1996), 1655–1662.Google Scholar