Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T05:08:40.288Z Has data issue: false hasContentIssue false
  • English
  • Français

KODAIRA DIMENSION OF UNIVERSAL HOLOMORPHIC SYMPLECTIC VARIETIES

Part of: Surfaces and higher-dimensional varieties Discontinuous groups and automorphic forms Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  02 February 2021

Shouhei Ma Open the ORCID record for Shouhei Ma [Opens in a new window]
Shouhei Ma*
Affiliation:
Department of Mathematics, Tokyo Institute of Technology, Tokyo152-8551, Japan ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the Kodaira dimension of the n-fold universal family of lattice-polarised holomorphic symplectic varieties with dominant and generically finite period map stabilises to the moduli number when n is sufficiently large. Then we study the transition of Kodaira dimension explicitly, from negative to nonnegative, for known explicit families of polarised symplectic varieties. In particular, we determine the exact transition point in the Beauville–Donagi and Debarre–Voisin cases, where the Borcherds 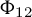$\Phi _{12}$ form plays a crucial role.

Keywords

holomorphic symplectic varietyuniversal familyKodaira dimensionmodular formBorcherds product

MSC classification

Primary: 14J15: Moduli, classification
Secondary: 11F55: Other groups and their modular and automorphic forms (several variables) 14G35: Modular and Shimura varieties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 1849 - 1866
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Footnotes

Supported by JSPS KAKENHI 15H05738 and 17K14158

References

Addington, N. and Lehn, M., On the symplectic eightfold associated to a Pfaffian cubic fourfold, J. Reine Angew. Math. 731 (2017), 129–137.Google Scholar
Beauville, A., Variétés Kähleriennes dont la première classe de Chern est nulle, J. Differential Geom. 18 (1983), 755–782.Google Scholar
Beauville, A. and Donagi, R., La variétés des droites d’une hypersurface cubique de dimension 4, C. R. Math. Acad. Sci. Paris 301 (1985), 703–706.Google Scholar
Borcherds, R., Automorphic forms on ${O}_{s+2,2}\left(\mathbb{R}\right)$ and infinite products, Invent. Math . 120(1) (1995), 161–213.CrossRefGoogle Scholar
Borcherds, R., Katzarkov, L., Pantev, T. and Shepherd-Barron, N. I., Families of K3 surfaces, J. Algebraic Geom. 7(1) (1998), 183–193.Google Scholar
Bruinier, J. H., On the rank of Picard groups of modular varieties attached to orthogonal groups, Compos. Math. 133(1) (2002), 49–63.CrossRefGoogle Scholar
Debarre, O., ‘Hyperkähler manifolds’, Preprint, 2018, https://arxiv.org/abs/1810.02087.Google Scholar
Debarre, O. and Voisin, C., Hyper-Kähler fourfolds and Grassmann geometry, J. Reine Angew. Math. 649 (2010), 63–87.Google Scholar
Gritsenko, V., Modular forms and moduli spaces of abelian and K3 surfaces, St. Petersburg Math. J. 6(6) (1995), 1179–1208.Google Scholar
Gritsenko, V., Hulek, K. and Sankaran, G., Moduli spaces of irreducible symplectic manifolds, Compos. Math. 146(2) (2010), 404–434.CrossRefGoogle Scholar
Gritsenko, V. A., Hulek, K. and Sankaran, G. K., Moduli of K3 surfaces and irreducible symplectic manifolds, in Handbook of Moduli, I, pp. 459–525 (International Press, Sommerville, 2013).Google Scholar
Iitaka, S., Algebraic Geometry, Graduate Texts in Mathematics, 76 (Springer, New York, 1982.CrossRefGoogle Scholar
Iliev, A., Kapustka, G., Kapustka, M. and Ranestad, K., EPW cubes, J. Reine Angew. Math. 748 (2019), 241–268.CrossRefGoogle Scholar
Iliev, A. and Ranestad, K., K3 surfaces of genus 8 and varieties of sums of powers of cubic fourfolds, Trans. Amer. Math. Soc. 353(4) (2001), 1455–1468.CrossRefGoogle Scholar
Iliev, A. and Ranestad, K., Addendum to “K3 surfaces of genus 8 and varieties of sums of powers of cubic fourfolds”, C. R. Acad. Bulgare Sci. 60 (2007), 1265–1270.Google Scholar
Kawamata, Y., Minimal models and the Kodaira dimension of algebraic fiber spaces, J. Reine. Angew. Math. 363 (1985), 1–46.Google Scholar
Laza, R., The moduli space of cubic fourfolds via the period map, Ann. of Math. (2) 172 (2010), 673–711.CrossRefGoogle Scholar
Lehn, C., Lehn, M., Sorger, C. and van Straten, D., Twisted cubics on cubic fourfolds, J. Reine Angew. Math. 731 (2017), 87–128.Google Scholar
Looijenga, E., The period map for cubic fourfolds, Invent. Math. 177 (2009), 213–233.CrossRefGoogle Scholar
Ma, S., Equivariant Gauss sum of finite quadratic forms, Forum Math. 30(4) (2018), 1029–1047.CrossRefGoogle Scholar
Ma, S., ‘Mukai models and Borcherds products’, Preprint, 2019, https://arxiv.org/abs/1909.03946.Google Scholar
Markman, E., A survey of Torelli and monodromy results for holomorphic-symplectic varieties, in Complex and Differential Geometry, pp. 257–322, (Springer, Berlin, 2011).CrossRefGoogle Scholar
Markman, E., ‘On the existence of universal families of marked irreducible holomorphic symplectic manifolds’, Preprint, 2017, https://arxiv.org/abs/1701.08690, to appear in Kyoto J. Math.Google Scholar
Mumford, D., Fogarty, J. and Kirwan, F., Geometric Invariant Theory (Springer, Berlin, 1994).CrossRefGoogle Scholar
Mongardi, G., ‘Automorphisms of Hyperkähler manifolds’, Ph.D. thesis, Università Roma Tre, 2013, available at https://arxiv.org/abs/1303.4670.Google Scholar
O’Grady, K. G., Irreducible symplectic 4-folds and Eisenbud-Popescu-Walter sextics, Duke Math. J. 134(1) (2006), 99–137.Google Scholar
O'Grady, K. G., Double covers of EPW-sextics, Michigan Math. J. 62 (2013), 143–184.Google Scholar
Voisin, C., Théorème de Torelli pour les cubiques de ${\mathbb{P}}^5$ , Invent. Math. 86 (1986), 577–601.CrossRefGoogle Scholar