Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T16:10:43.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Iwasawa theory of de Rham $(\varphi , \Gamma )$-modules over the Robba ring

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  27 February 2013

Kentaro Nakamura
Kentaro Nakamura*
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060-0810, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

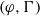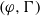The aim of this article is to study the Bloch–Kato exponential map and the Perrin-Riou big exponential map purely in terms of $(\varphi , \Gamma )$-modules over the Robba ring. We first generalize the definition of the Bloch–Kato exponential map for all the 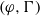$(\varphi , \Gamma )$-modules without using Fontaine’s rings 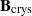${\mathbf{B} }_{\mathrm{crys} } $, 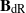${\mathbf{B} }_{\mathrm{dR} } $ of 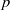$p$-adic periods, and then generalize the construction of the Perrin-Riou big exponential map for all the de Rham 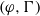$(\varphi , \Gamma )$-modules and prove that this map interpolates our Bloch–Kato exponential map and the dual exponential map. Finally, we prove a theorem concerning the determinant of our big exponential map, which is a generalization of theorem 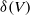$\delta (V)$ of Perrin-Riou. The key ingredients for our study are Pottharst’s theory of the analytic Iwasawa cohomology and Berger’s construction of 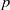$p$-adic differential equations associated to de Rham 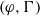$(\varphi , \Gamma )$-modules.

Keywords

p-adic Hodge theory(φ,Γ)-moduleB-pair

MSC classification

Secondary: 11F80: Galois representations 11F85: $p$-adic theory, local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 1 , January 2014 , pp. 65 - 118
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, Y., Filtrations de Hasse-Arf et monodromie $p$-adique, Invent. Math. 148 (2002), 285–317.Google Scholar
Benois, D., On Iwasawa theory of crystalline representations, Duke Math. J. 104 (2000), 211–267.Google Scholar
Berger, L., Représentations $p$-adiques et équations différentielles, Invent. Math. 148 (2002), 219–284.Google Scholar
Berger, L., Bloch and Kato’s exponential map: three explicit formulas. Doc. Math, (2003), 99–129 (electronic). Kazuya Kato’s fiftieth birthday.Google Scholar
Berger, L., Construction de ($\varphi , \Gamma $)-modules: représentations $p$-adiques et $B$-paires, Algebra Number Theory 2 (1) (2008), 91–120.Google Scholar
Berger, L., Équations différentielles $p$-adiques et ($\varphi , N$)-modules filtres, Astérisque (319) (2008), 13–38, Représentations $p$-adiques de groupes $p$-adiques. I. Représentations galoisiennes et ($\varphi , N$)-modules.Google Scholar
Bloch, S. and Kato, K., $L$-functions and Tamagawa numbers of motives, in The Grothendieck Festschrift, Vol. I, Progress in Mathematics, Volume 86, pp. 333–400 (Birkhäuser Boston, Boston, MA, 1990).Google Scholar
Cherbonnier, F. and Colmez, P., Représentations $p$-adiques surconvergentes, Invent. Math. 133 (1998), 581–611.Google Scholar
Cherbonnier, F. and Colmez, P., Théorie d’Iwasawa des représentations $p$-adiques dun corps local, J. Amer. Math. Soc. 12 (1999), 241–268.Google Scholar
Chenevier, G., Sur la densité des representations cristallines de $\mathrm{Gal} ({ \overline{ \mathbb{Q} } }_{p} / { \mathbb{Q} }_{p} )$, Math. Ann. (2012).Google Scholar
Colmez, P., Théorie d’Iwasawa des représentations de de Rham d’un corps local, Ann. of Math. 148 (1998), 485–571.CrossRefGoogle Scholar
Crew, R., Finiteness theorems for the cohomology of an overconvergent isocrystal on a curve, Ann. Sci. Éc. Norm. Supér. (4) 31 (6) (1998), 717–763.Google Scholar
Fontaine, J.-M., Représentations $p$-adiques des corps locaux I, in The Grothendieck Festschrift, Vol. 2, Progress in Mathematics, Volume 87, pp. 249–309 (Birkhäuser, Boston, 1990).Google Scholar
Fontaine, J.-M., Le corps des périodes $p$-adiques, Astérisque 223 (1994), 59–111.Google Scholar
Fontaine, J.-M., Presque ${ \mathbb{C} }_{p} $-représentations, Kazuya Kato’s fifties birthday, Doc. Math., (2003), Extra Vol., 285–385 (electronic).Google Scholar
Herr, L., Sur la cohomologie galoisienne des corps $p$-adiques, Bull. Soc. Math. France 126 (4) (1998), 563–600.Google Scholar
Herr, L., Une approche nouvelle de la dualité locale de Tate, Math. Ann. 320 (2) (2001), 307–337.Google Scholar
Kato, K., Lectures on the approach to Iwasawa theory for Hasse-Weil $L$-functions via ${\mathbf{B} }_{\mathrm{dR} } $, in Arithmetic algebraic geometry, Lecture Notes in Mathematics, Volume 1553, pp. 50–63 (Springer, Berlin, 1993).CrossRefGoogle Scholar
Kato, K., Lectures on the approach to Iwasawa theory for Hasse-Weil $L$-functions via ${\mathbf{B} }_{\mathrm{dR} } $. II, preprint (1993).Google Scholar
Kato, K., $p$-adic Hodge theory and values of zeta functions of modular forms, Astérisque ix (295) (2004), 117–290, Cohomologies $p$-adiques et applications arithmétiques. III.Google Scholar
Kato, K., Kurihara, M. and Tsuji, T., Local Iwasawa theory of Perrin-Riou and syntomic complexes, preprint (1996).Google Scholar
Kedlaya, K., A $p$-adic local monodromy theorem, Ann. of Math. (2) 160 (2004), 93–184.CrossRefGoogle Scholar
Liu, R., Cohomology and duality for ($\varphi , \Gamma $)-modules over the Robba ring, Int. Math. Res. Not. IMRN (3) (2008).Google Scholar
Mebkhout, Z., Analogue $p$-adique du théorème de Turrittin et le théorème de la mon- odromie $p$-adique, Invent. Math. 148 (2002), 319–351.CrossRefGoogle Scholar
Nakamura, K., Classification of two dimensional split trianguline representations of $p$-adic fields, Compositio Math. 145 (2009), 865–914.Google Scholar
Nakamura, K., Deformations of trianguline $B$-pairs and Zariski density of two dimensional crystalline representations, preprint (arXiv:1006.4891 [math.NT]).Google Scholar
Nakamura, K., A generalization of Kato’s local $\varepsilon $-conjecture for $(\varphi , \Gamma )$-modules over the Robba ring, in preparation.Google Scholar
Perrin-Riou, B., Théorie d’Iwasawa et hauteurs $p$-adiques, Invent. Math. 109 (1992), 137–185.Google Scholar
Perrin-Riou, B., Théorie d’Iwasawa des représentations $p$-adiques sur un corps local, Invent. Math. 115 (1994), 81–161.CrossRefGoogle Scholar
Perrin-Riou, B., Fonctions $L\hspace{0.167em} p$-adiques des représentations $p$-adiques, Astérisque (229)(1995), 198 pp.Google Scholar
Pottharst, J., Analytic families of finite-slope Selmer groups, preprint on his web page.Google Scholar
Pottharst, J., Cyclotomic Iwasawa theory of motives, preprint on his web page.Google Scholar
Schneider, P. and Teitelbaum, J., Algebras of $p$-adic distributions and admissible representations, Invent. Math. 153 (1) (2003), 145–196.Google Scholar