Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T08:26:08.897Z Has data issue: false hasContentIssue false
  • English
  • Français

INHOMOGENEOUS INCOMPRESSIBLE VISCOUS FLOWS WITH SLOWLY VARYING INITIAL DATA

Part of: Incompressible viscous fluids Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  03 November 2016

Jean-Yves Chemin  and
Ping Zhang
Jean-Yves Chemin
Affiliation:
Laboratoire J.-L. Lions, UMR 7598, Université Pierre et Marie Curie, 75230 Paris Cedex 05, France ([email protected])
Ping Zhang
Affiliation:
Academy of Mathematics & Systems Science and Hua Loo-Keng Key Laboratory of Mathematics, The Chinese Academy of Sciences, Beijing 100190, China School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this paper is to provide a large class of initial data which generates global smooth solution of the 3D inhomogeneous incompressible Navier–Stokes system in the whole space 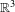$\mathbb{R}^{3}$. This class of data is based on functions which vary slowly in one direction. The idea is that 2D inhomogeneous Navier–Stokes system with large data is globally well-posed and we construct the 3D approximate solutions by the 2D solutions with a parameter. One of the key point of this study is the investigation of the time decay properties of the solutions to the 2D inhomogeneous Navier–Stokes system. We obtained the same optimal decay estimates as the solutions of 2D homogeneous Navier–Stokes system.

Keywords

inhomogeneous incompressible Navier–Stokes equationsslow variabledecay estimateanisotropic Littlewood–Paley theory

MSC classification

Primary: 35Q30: Navier-Stokes equations
Secondary: 76D03: Existence, uniqueness, and regularity theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 5 , November 2018 , pp. 1121 - 1172
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abidi, H., Équations de Navier–Stokes avec densité et viscosité variables dans l’espace critique, Rev. Mat. Iberoam. 23 (2007), 537–586.Google Scholar
Abidi, H. and Paicu, M., Existence globale pour un fluide inhomogène, Ann. Inst. Fourier 57 (2007), 883–917.Google Scholar
Abidi, H., Gui, G. and Zhang, P., On the wellposedness of 3-D inhomogeneous Navier–Stokes equations in the critical spaces, Arch. Ration Mech. Anal. 204 (2012), 189–230.Google Scholar
Abidi, H., Gui, G. and Zhang, P., Wellposedness of 3-D inhomogeneous Navier–Stokes equations with highly oscillating initial velocity field, J. Math. Pures Appl. (9) 100 (2013), 166–203.Google Scholar
Bahouri, H., Chemin, J.-Y. and Danchin, R., Fourier Analysis and Nonlinear Partial Differential Equations, Grundlehren der Mathematischen Wissenschaften (Springer, 2010).Google Scholar
Brandolese, L., Space-time decay of Navier–Stokes flows invariant under rotations, Math. Ann. 329 (2004), 685–706.Google Scholar
Chemin, J.-Y. and Gallagher, I., Large, global solutions to the Navier–Stokes equations, slowly varying in one direction, Trans. Amer. Math. Soc. 362 (2010), 2859–2873.Google Scholar
Chemin, J.-Y., Gallagher, I. and Paicu, M., Global regularity for some classes of large solutions to the Navier–Stokes equations, Ann. of Math. (2) 173 (2011), 986–1012.Google Scholar
Chemin, J.-Y., Gallagher, I. and Zhang, P., Sums of large global solutions to the incompressible Navier–Stokes equations, J. Reine Angew. Math. 681 (2013), 65–82.Google Scholar
Chemin, J.-Y., Paicu, M. and Zhang, P., Global large solutions to 3-D inhomogeneous Navier–Stokes system with one slow variable, J. Differential Equations 256 (2014), 223–252.Google Scholar
Chemin, J.-Y. and Zhang, P., On the global wellposedness to the 3-D incompressible anisotropic Navier–Stokes equations, Commun. Math. Phys. 272 (2007), 529–566.Google Scholar
Chemin, J.-Y. and Zhang, P., On the critical one component regularity for 3-D Navier–Stokes system, Ann. Éc. Norm. Supér. 49 (2016), 131–167.Google Scholar
Chemin, J.-Y. and Zhang, P., Remarks on the global solutions of 3-D Navier–Stokes system with one slow variable, Comm. Partial Differential Equations 40 (2015), 878–896.Google Scholar
Chemin, J.-Y. and Zhang, P., Inhomogeneous incompressible viscous flows with slowly varying initial data, arXiv:1505.07724 [math.AP].Google Scholar
Danchin, R., Density-dependent incompressible viscous fluids in critical spaces, Proc. Roy. Soc. Edinburgh Sect. A 133 (2003), 1311–1334.Google Scholar
Danchin, R. and Mucha, P., A Lagrangian approach for the incompressible Navier–Stokes equations with variable density, Comm. Pure Appl. Math. 65 (2012), 1458–1480.Google Scholar
Danchin, R. and Mucha, P. B., Incompressible flows with piecewise constant density, Arch. Ration Mech. Anal. 207 (2013), 991–1023.Google Scholar
Danchin, R. and Zhang, P., Inhomogeneous Navier–Stokes equations in the half-space, with only bounded density, J. Funct. Anal. 267 (2014), 2371–2436.Google Scholar
He, C. and Miyakawa, T., On two-dimensional Navier–Stokes flows with rotational symmetries, Funkcial. Ekvac. 49 (2006), 163–192.Google Scholar
Huang, J., Paicu, M. and Zhang, P., Global well-posedness of incompressible inhomogeneous fluid systems with bounded density or non-Lipschitz velocity, Arch. Ration Mech. Anal. 209 (2013), 631–682.Google Scholar
Gallagher, I., Iftimie, D. and Planchon, F., Asymptotics and stability for global solutions to the Navier–Stokes equations, Ann. Inst. Fourier (Grenoble) 53 (2003), 1387–1424.Google Scholar
Kazhikov, A. V., Solvability of the initial-boundary value problem for the equations of the motion of an inhomogeneous viscous incompressible fluid (Russian), Dokl. Akad. Nauk SSSR 216 (1974), 1008–1010.Google Scholar
Ladyženskaja, O.-A. and Solonnikov, V.-A., The unique solvability of an initial-boundary value problem for viscous incompressible inhomogeneous fluids. (Russian) Boundary value problems of mathematical physics, and related questions of the theory of functions, 8, Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 52 (1975), 52–109, 218–219.Google Scholar
Lions, P.-L., Mathematical topics in fluid mechanics. Vol. 1. Incompressible Models, Oxford Lecture Series in Mathematics and its Applications, 3 (Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1996).Google Scholar
Miyakawa, T. and Schonbek, M.-E., On optimal decay rates for weak solutions to the Navier–Stokes equations in R n , Math. Bohem. 126 (2001), 443–455.Google Scholar
Paicu, M., Équation anisotrope de Navier–Stokes dans des espaces critiques, Rev. Mat. Iberoam. 21 (2005), 179–235.Google Scholar
Paicu, M. and Zhang, P., Global solutions to the 3-D incompressible inhomogeneous Navier–Stokes system, J. Funct. Anal. 262 (2012), 3556–3584.Google Scholar
Paicu, M., Zhang, P. and Zhang, Z., Global well-posedness of inhomogeneous Navier–Stokes equations with bounded density, Comm. Partial Differential Equations 38 (2013), 1208–1234.Google Scholar
Paicu, M. and Zhang, P., On some large global solutions to 3-D density-dependent Navier–Stokes system with slow variable: well-prepared data, Ann. Inst. Henri Poincare Non Linear Anal. 32 (2015), 813–832.Google Scholar
Schonbek, M., Lower bounds of rates of decay for solutions to the Navier–Stokes equations, J. Amer. Math. Soc. 4 (1991), 423–449.Google Scholar
Schonbek, M. and Schonbek, T., On the boundedness and decay of moments of solutions of the Navier Stokes equations, Adv. Differential Equations 5 (2000), 861–898.Google Scholar
Simon, J., Nonhomogeneous viscous incompressible fluids: existence of velocity, density, and pressure, SIAM J. Math. Anal. 21 (1990), 1093–1117.Google Scholar
Wiegner, M., Decay results for weak solutions to the Navier–Stokes equations on ℝ n , J. Lond. Math. Soc. (2) 35 (1987), 303–313.Google Scholar