Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T09:33:03.116Z Has data issue: false hasContentIssue false
  • English
  • Français

II1 FACTORS WITH EXOTIC CENTRAL SEQUENCE ALGEBRAS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  19 December 2019

Adrian Ioana Open the ORCID record for Adrian Ioana [Opens in a new window]  and
Pieter Spaas
Adrian Ioana
Affiliation:
Department of Mathematics, University of California San Diego, 9500 Gilman Drive, La Jolla, CA92093, USA ([email protected]; [email protected])
Pieter Spaas
Affiliation:
Department of Mathematics, University of California San Diego, 9500 Gilman Drive, La Jolla, CA92093, USA ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

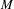We provide a class of separable II1 factors $M$ whose central sequence algebra is not the ‘tail’ algebra associated with any decreasing sequence of von Neumann subalgebras of 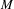$M$. This settles a question of McDuff [On residual sequences in a II1 factor, J. Lond. Math. Soc. (2) (1971), 273–280].

Keywords

II1 factorcentral sequence algebraresidual sequenceGaussian actiontracial stabilitydeformation rigidity theory

MSC classification

Primary: 46L10: General theory of von Neumann algebras
Secondary: 46L36: Classification of factors
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 5 , September 2021 , pp. 1671 - 1696
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors were supported in part by NSF Career Grant DMS #1253402.

References

Atkinson, S., Some results on tracial stability and graph products, Preprint, 2018, arXiv:1808.04664.Google Scholar
Boutonnet, R., On solid ergodicity for Gaussian actions, J. Funct. Anal. 263(4) (2012), 1040–1063.Google Scholar
Boutonnet, R., Plusieurs aspects de rigidité des algèbres de von Neumann, PhD Thesis (2014).Google Scholar
Boutonnet, R., Chifan, I. and Ioana, A., II1 factors with non-isomorphic ultrapowers, Duke Math. J. 166(11) (2017), 2023–2051.Google Scholar
Chifan, I. and Udrea, B., Some rigidity results for II1 factors arising from wreath products of property (T) groups, Preprint, 2018, arXiv:1804.04558.Google Scholar
Ching, W.-M., Non-isomorphic non-hyperfinite factors, Canad. J. Math. 21 (1969), 1293–1308.Google Scholar
Choda, M., Inner amenability and fullness, Proc. Amer. Math. Soc. 86 (1982), 663–666.Google Scholar
Connes, A., Classification of injective factors, Ann. of Math. (2) 104(1) (1976), 73–115.Google Scholar
Connes, A., Noncommutative Geometry (Academic Press, Inc., San Diego, CA, 1994). xiv+661 pp.Google Scholar
Dixmier, J. and Lance, E. C., Deux nouveaux facteurs de type II1 , Invent. Math. 7 (1969), 226–234.Google Scholar
Drimbe, D., Hoff, D. and Ioana, A., Prime II1 factors arising from irreducible lattices in products of rank one simple Lie groups, J. Reine. Angew. Math. 757 (2019), 197–246.Google Scholar
Fang, J., Ge, L. and Li, W., Central sequence algebras of von Neumann algebras, Taiwanese J. Math. 10 (2006), 187–200.Google Scholar
Farah, I., Hart, B. and Sherman, D., Model theory of operator algebras III: elementary equivalence and II1 factors, Bull. Lond. Math. Soc. 46 (2014), 609–628.Google Scholar
Goldbring, I. and Hart, B., On the theories of McDuff’s II1 factors, Int. Math. Res. Not. IMRN 27(18) (2017), 5609–5628.Google Scholar
Haagerup, U., An example of a non-nuclear C ∗-algebra, which has the metric approximation property, Invent. Math. 50 (1978/79), 279–293.Google Scholar
Hadwin, D. and Shulman, T., Tracial stability for C ∗-algebras, Integral Equations Operator Theory 90(1) (2018).Google Scholar
Hadwin, D. and Shulman, T., Stability of group relations under small Hilbert–Schmidt perturbations, J. Funct. Anal. 275(4) (2018), 761–792.Google Scholar
Houdayer, C., Structure of II1 factors arising from free Bogoljubov actions of arbitrary groups, Adv. Math. 260 (2014), 414–457.Google Scholar
Houdayer, C. and Ueda, Y., Rigidity of free product von Neumann algebras, Compos. Math. 152 (2016), 2461–2492.Google Scholar
Ioana, A., Rigidity for von Neumann algebras, in Proc. Int. Cong. of Math. 2018 Rio de Janeiro, Vol. 2, pp. 1635–1668. (2018).Google Scholar
Ioana, A. and Spaas, P., A class of II1 factors with a unique McDuff decomposition, Preprint, 2018, arXiv:1808.02965.Google Scholar
Isono, Y., On fundamental groups of tensor product II1 factors, J. Inst. Math. Jussieu. 1–19. doi:10.1017/S1474748018000336.Google Scholar
Jones, V.F.R. and Schmidt, K., Asymptotically invariant sequences and approximate finiteness, Amer. J. Math. 109(1) (1987), 91–114.Google Scholar
Marrakchi, A., Stability of products of equivalence relations, Compos. Math. 154(9) (2018), 2005–2019.Google Scholar
McDuff, D., A countable infinity of II1 factors, Ann. of Math. (2) 90 (1969), 361–371.Google Scholar
McDuff, D., Uncountably many II1 factors, Ann. of Math. (2) 90 (1969), 372–377.Google Scholar
McDuff, D., Central sequences and the hyperfinite factor, Proc. Lond. Math. Soc. (3) 21 (1970), 443–461.Google Scholar
McDuff, D., On residual sequences in a II1 factor, J. Lond. Math. Soc. (2) 3 (1971), 273–280.Google Scholar
Murray, F. and von Neumann, J., Rings of operators, IV, Ann. of Math. (2) 44 (1943), 716–808.Google Scholar
Ozawa, N., Solid von Neumann algebras, Acta Math. 192 (2004), 111–117.Google Scholar
Ozawa, N. and Popa, S., On a class of II1 factors with at most one Cartan subalgebra, Ann. of Math. (2) 172(1) (2010), 713–749.Google Scholar
Peterson, J. and Sinclair, T., On cocycle superrigidity for Gaussian actions, Ergodic Theory Dynam. Systems 32 (2012), 249–272.Google Scholar
Popa, S., Correspondences, INCREST preprint 56 (1986), available at www.math.ucla.edu/∼popa/preprints.html.Google Scholar
Popa, S., Some rigidity results for non-commutative Bernoulli shifts, J. Funct. Anal. 230 (2006), 273–328.Google Scholar
Popa, S., Strong rigidity of II1 factors arising from malleable actions of w-rigid groups. I, Invent. Math. 165(2) (2006), 369–408.Google Scholar
Popa, S., On the superrigidity of malleable actions with spectral gap, J. Amer. Math. Soc. 21 (2008), 981–1000.Google Scholar
Popa, S., On Ozawa’s property for free group factors, Int. Math. Res. Not. IMRN 2007(11) (2007), Art. ID rnm036, 10 pp.Google Scholar
Popa, S., Deformation and rigidity for group actions and von Neumann algebras, in Proceedings of the International Congress of Mathematicians (Madrid, 2006), Volume I, pp. 445–477 (European Mathematical Society Publishing House, Zurich, 2007).Google Scholar
Popa, S., On spectral gap rigidity and Connes invariant 𝜒(M), Proc. Amer. Math. Soc. 138(10) (2010), 3531–3539.Google Scholar
Popa, S., On the classification of inductive limits of II1 factors with spectral gap, Trans. Amer. Math. Soc. 364 (2012), 2987–3000.Google Scholar
Sakai, S., The Theory of W*-Algebras, Lecture Notes, (Yale University, 1962).Google Scholar
Sakai, S., Asymptotically abelian II1-factors, Publ. Res. Inst. Math. Sci. Ser. A 4 (1968/1969), 299–307.Google Scholar
Sinclair, T., Strong solidity of group factors from lattices in SO(n,1) and SU(n,1), J. Funct. Anal. 260 (2011), 3209–3221.Google Scholar
Thom, A., Finitary approximations of groups and their applications, in Proc. Int. Cong. of Math. 2018 Rio de Janeiro, Vol. 2, pp. 1775–1796. (2018).Google Scholar
Vaes, S., Rigidity for von Neumann algebras and their invariants, in Proceedings of the ICM (Hyderabad, India, 2010), Volume III, pp. 1624–1650 (Hindustan Book Agency, New Dehli, 2010).Google Scholar
Vaes, S., One-cohomology and the uniqueness of the group measure space of a II1 factor, Math. Ann. 355 (2013), 661–696.Google Scholar
Voiculescu, D.-V., Dykema, K. J. and Nica, A., Free Random Variables, CRM Monograph Series, Volume 1, (AMS, Providence, RI, 1992).Google Scholar
Wright, F. B., A reduction for algebras of finite type, Ann. of Math. (2) 60 (1944), 560–570.Google Scholar
Zeller-Meier, G., Deux autres facteurs de type II1 , Invent. Math. 7 (1969), 235–242. (French).Google Scholar